Paper Menu >>
Journal Menu >>
 Journal of Modern Physics, 2013, 4, 48-53 doi:10.4236/jmp.2013.45B010 Published Online May 2013 (http://www.scirp.org/journal/jmp) Coherent Resonance of Saturated Absorption in Spectroscopy of Counterpropagating Waves A. A. Chernenko1, E. G. Saprykin2, A. M. Shalagin2,3 1Institute of Semiconductor Physics, Siberian Branch, Russian Academy of Sciences, Novosibirsk, Russia 2Institute of Automation and Electrometry, Siberian Branch, Russian Academy of Sciences, Novosibirsk, Russia 3Novosibirsk State University, Novosibirsk, Russia Email: chernen@isp.nsc.ru Received 2013 ABSTRACT Results of theoretical researches of the saturated absorption resonance shape in a method of the probing field on V-type of transitions are represented. It is shown that in case of opposite circulary polarized optical fields the resonance is shown in the form of cross, and its form strongly depends on relaxation constants of levels and it can be represented as in the form of a dip, and absorption peak. Thus, the peak form has exclusively coherent character. Atomic transitions are offered, on which observation of the given effect is possible. Keywords: Nonlinear Spectroscopy; Atomic Transition; Saturation Absorption; Cross Resonance; Light Wave 1. Introduction It is known that action of the strong light fields on a resonant medium leads to nonlinear effects which are shown in the form of change of the density populations of resonant levels (effect of saturation), splitting of levels and an interference of levels – so-called nonlinear inter- ferential effect (NIEF) as result of simultaneous absorp- tion some photons [1]. The effect of saturation has exclu- sively incoherent character, and two others are caused by coherent processes. The method of a probing field [1,2] allows investigating the specified nonlinear effects. The resonance registered in this method in the absorption spectrum of the probing field by the resonant gas me- dium is shown in the form of a dip on the Doppler line contour and carries generally incoherent (populational) character. The coherent processes are shown in a form of the field broadening of the resonance spectrum (effect of level splitting) and as an additive in the dip amplitude (contribution of NIEF). And, the value of the NIEF con- tribution depends on the direction of propagation of the strong and probing light wave; effect is maximum at uni- directional waves, and in case of opposite directed waves the contribution of effect to resonance amplitude is strongly suppressed (in relation of the uniform width to the Dop- pler line width of atomic transition). So for the two-level medium under optimum conditions the share of NIEF in amplitude of a resonance doesn’t exceed some percent [2]. In spite of the fact that researches on nonlinear spec- troscopy of multilevel quantum systems are conducted already for a long time, a situation when the nonlinear resonance in opposite directed waves would be defined by only coherent processes, as far as we know, isn’t found until now. There are cases, as in paper [3] where to the observed spectrum features of the nonlinear reso- nance, having the incoherent nature, NIEF manifestation was mistakenly attributed. In this work we consider quantum system in which in case of the opposite directed light waves the nonlinear resonance having exclusively coherent nature (without a contribution of populated effects) with characteristic for coherent processes by an interferential form of a spec- trum can be observed. Such situation is realized in the V-type of transitions the upper state of which has to breaks up only in the bottom state, and light waves have to be circular polarized with the counter direction of ro- tation of polarization vectors. A number of atomic transi- tions on which probably experimental observation of a resonance of coherent type is offered. 2. Theoretical Model Let us consider the problem about the absorption spec- trum of a probing field in a medium with V-type of tran- sition in the presence of a strong field with the same fre- quency and opposite propagation direction. The scheme of transitions is presented in Figure 1. The strong wave is assumed to be plane (with the frequency , wave vec- tor k, and electric field strength Е) and resonant to the atomic transition m – n (with the transition frequency mn). Polarization of the strong wave is either linear or circular (separate case). The probe wave is also mono- Copyright © 2013 SciRes. JMP  A. A. CHERNENKO ET AL. 49 chromatic (with the frequency = , the wave vector k = – k, and the electric field strength Е) with circular polarization. When solving the problem, the saturation of a medium by the probing wave is taking into account under the assumption of its weakness as compared to the strong wave. The gas is assumed to be rarefied enough to neglect collisions. The medium is assumed to be opti- cally thin. We consider the problem in a coordinate system with the quantization exis along the direction of wave vector k of the strong field. In this coordinate system light fields induces transitions between magnetic sublevels (Figure 1) with variation М = ± 1 (at linear polarization), or transitions with М = +1 or М = –1 (at circular polari- zation depending on a direction of its rotation). In solving the problem we start from kinetic equations for a density matrix of the atomic system. According to [1], the dynamics of diagonal elements of the density matrix ( i = ii) in the model of relaxation constants is described by the system of equations: 2Re() 2Re() i i iiki kijji kj ij ji j Qi t iV V (1) For off-diagonal elements of the density matrix the next system is valid: ()[,][, ik ikik ikikik iiViV t ] (2) Here Гi and Гik are the widths of the levels and transi- tions, Qi is the number of exitation acts of the i-th level per unit time, the summand ki k k in system of equations (1) determines the spontaneous decay of the upper state m to the lower state n and is absent in the equations for the populations of upper levels, V and V are operators of the interaction between the atom and the strong and probing fields. The operators are defined as V = – Gexp(i(kr – t)) +H.с. and V = – G exp(i(k r – t)) +H.с., where the operators G = dE2, and G = dE 2, and d is the operator of the reduced dipole moment of atomic transition. Let's mark, that the given statement of the problem and the obtained solutions are fair both for transitions between exited states, and for a case, when the lower state n is the ground state of atom. In this case the width of the lower state is determined by mean value of the interaction time of particles with the light fields. Following [1], we seek solutions of the system of equations for the density matrix in the following form (the first harmonic approximation by the difference of wave frequencies = – ): the diagonal elements are found as i = i 0 + i +exp(i t) + i -exp(–i t); off-diagonal cordingly are found as ik = Rik exp(–it) + Rik exp(–i t) + Rik s exp(–ist) and ik = rik 0 + rik +exp(i t) + rik -exp(–i t), where s = 2 – . The substantiation of the given kind of solutions and their accuracies for the V-, Λ- and J = 1-J =1 types of transitions are given by us in works [4,5]. In the approximation of rotating optical fields the sys- elements on the allowed and forbidden transitions ac- te lations of th m of equations for the density matrix in the considered transition scheme in the stationary case is reduced to a system of algebraic equations for i 0, i , Rik, Rik , R ik s, rik 0, and rik . Taking into account the hermiticity of these coefficients, we write only independent equations for a case of the linear polarized strong field. The equations for a case of the circular polarized strong field are easily received from reduced below, equating to zero one of the circular strength component of strong field. In a case of the V- scheme (Figure 1) popu e lower (0) and the upper (1 and 2) levels are described by a following system of equations: 00 2R 00 0 00 1, 21, 2 02 20 e( ) 2Re() QA nkk kk iGR iG R kk (3a) ) 0001 100220 1,2 02 2020 0210 01 () ( () ss nkk k iAiGRG iGRGRG R R (3б) (3в) 0 0 1110 01 2Re( ) mQiGR 11001011 ()( ) s miiGRGR (3г) 0 2220 0220 02 2Re()2Re() mQiGR iGR (3д) 22002 02200220 ()( s miiGRGRGR ) The system of equations for polarizations lo (3е) at the al- wed (1– 0 and 2– 0 ) and at the forbidden 2– 1 transi- tions has the next form: 0 1 2 n m 2∆ Figure 1. Scheme of interaction of light fields with V-type of atomic transitions, - shift of levels. Copyright © 2013 SciRes. JMP  A. A. CHERNENKO ET AL. 50 00 0 1001011002 2102 21 ()() mn iRiGiG riG r (4a) 1001011002 21 (( ))() s mn iRiGiG r (4б) 0 2 21 r (4в) 10 01101002 210 ()() mn iRiGiG riG 00 20 2020 2020 20 0 10 21 () ()( mn i RiGiG iG r ) (4г) 202020201021 (( ))() s mn iRiGiG r (4д) 00 20 2020 2020 20 10 21 () ()( mn i RiGiG iG r ) ) (4е) 0 2121200101 2020 01 ()( miriGRGRGR ) (5а) 2121200101 20 (( ))( s miriGRG R (5б) 2121200101 20 (( ))( 2001 ) s miriGRGR GR (5в) In equations (3) - (5) Гn and Гm are the widths lower and upper levels, Гmn is the width of the tran lin anges in the equations: atom. The situation of co ollowing relation: erical Solution of the Initial Equations b- taits of the density matrix were of the sition e, 21 is the width of the forbidden transition between magnetic sublevels of the upper state; ik = – ik and ik = – ik are the values of frequency detuning of the strong and probing fields from the frequencies ik of transitions between the magnetic sublevels of the m and n states. The motion of atoms is taken into account by the fol- lowing ch ik ik – kv, ik ik – k v, аnd – (k – k)v, where v is the velocity of unter propagation of waves with equal frequencies was then analyzed: = , and k = – k. The shape of the absorption line of the probing field (per atom) was determined by the f /0 = – mn Re(i(R20 ))/G , where the designation <...> means the averaging by the Maxwell velocity dis- tribution of particles, and 0 = 4 mnd2/cmn is the resonant absorption cross section. In calculations the probabilities Aki of the decay of magnetic sublevels by each of the spontaneous channels were set to be similar and equal to Amn/2. 3. Results of Num Stationary system of equations (3) - (5) that were o ned above for elemen solved numerically upon varying the values of width of the upper Гm and lower Гn atom levels, the parameter of the radiation branching from the upper level а0 (a0 = Amn/Γm) and the intensities of optical fields using the relaxation characteristics of the 1s2 - 2p8 transition of the neon atom (Аmn = 1.88 × 107 с-1, Гm = 5.5 × 107 с-1, Гn = 105 106 с–1, Гmn = (Гm + Гn)/2). The values of level widths varied from the aforesaid values to Гm = Гn = Гmn, at the same time, the transition width Гmn remained con- stant and the value of branching parameter а0 varied within the range 0.34 1. The line width of the forbidden transition between the sublevels of the upper state relied to width of the upper level. The Doppler line width is taken to be equal kvT = 5.2×109 с-1, and the variation range of particle velocities at integration was 3kvT with a step kvT = (10-3 ÷ 10-4)kvT. The saturation parameters of the strong (κs) and probing (κp) fields were chosen in the form 2 2(/2)/ () s mn n dE and 2 2(/ 2)/ ()dE , pm nn where E and E are the hs of the circular compo nents of the strong and ng fields and d is the re- tion spec- ion in the the cross resonance can m strengt- probi duced dipole moment of transition. The values of satura- tion parameters varied within the limits κs 50 and κp κs. Below, results are presented for small value of the saturation parameter of the probing field κp = 10-3. 3.1. Strong Field of Linear Polarization Results of numerical simulation of the absorp trum of the probing wave of circular polarizat presence of a strong saturating field of linear polarization are presented in Figures 2 and 3. When the upper state is degenerated the shape of the nonlinear resonance is rep- resented as a dip in the center of the Doppler contour of the absorption line. Its amplitude and width depend on the saturation parameters of optical fields, on width of transition level and on the branching parameter а0. With elimination of the degeneracy (splitting) of the upper levels one can observe a dip of the saturated absorption at the shifted transition frequency in the shape of the ab- sorption line of the circular polarized probing wave (named as РR, the sign of its shift is defined by the sign of circular polarization) and a cross resonance (CR) at the unshifted frequency тn. Amplitude and sign of the cross resonance depend essentially on the relation be- tween the level widths Гm and Гn and on the branching parameter а0, at the same time, the effect of these char- acteristics on the parameters of the parent (PR) resonance is expressed much weaker. It is seen from Figure 2 that, depending on the value of the branching parameter a0, anifest itself not only as a dip, but also as an absorption peak. The maximal value of the peak amplitude is reached for the closed transition (for parameter а0 = 1) both when the values of the level widths are similar (Гm Гn) and when they are considerably different (Гm >> Гn). Thus it appears, that at a similar values of the saturation parame- ters κs of the strong field, the peak amplitude in case of similar values of level width is considerably larger than the peak amplitude in case of a strong difference between the widths (curves 1 and 5). Copyright © 2013 SciRes. JMP 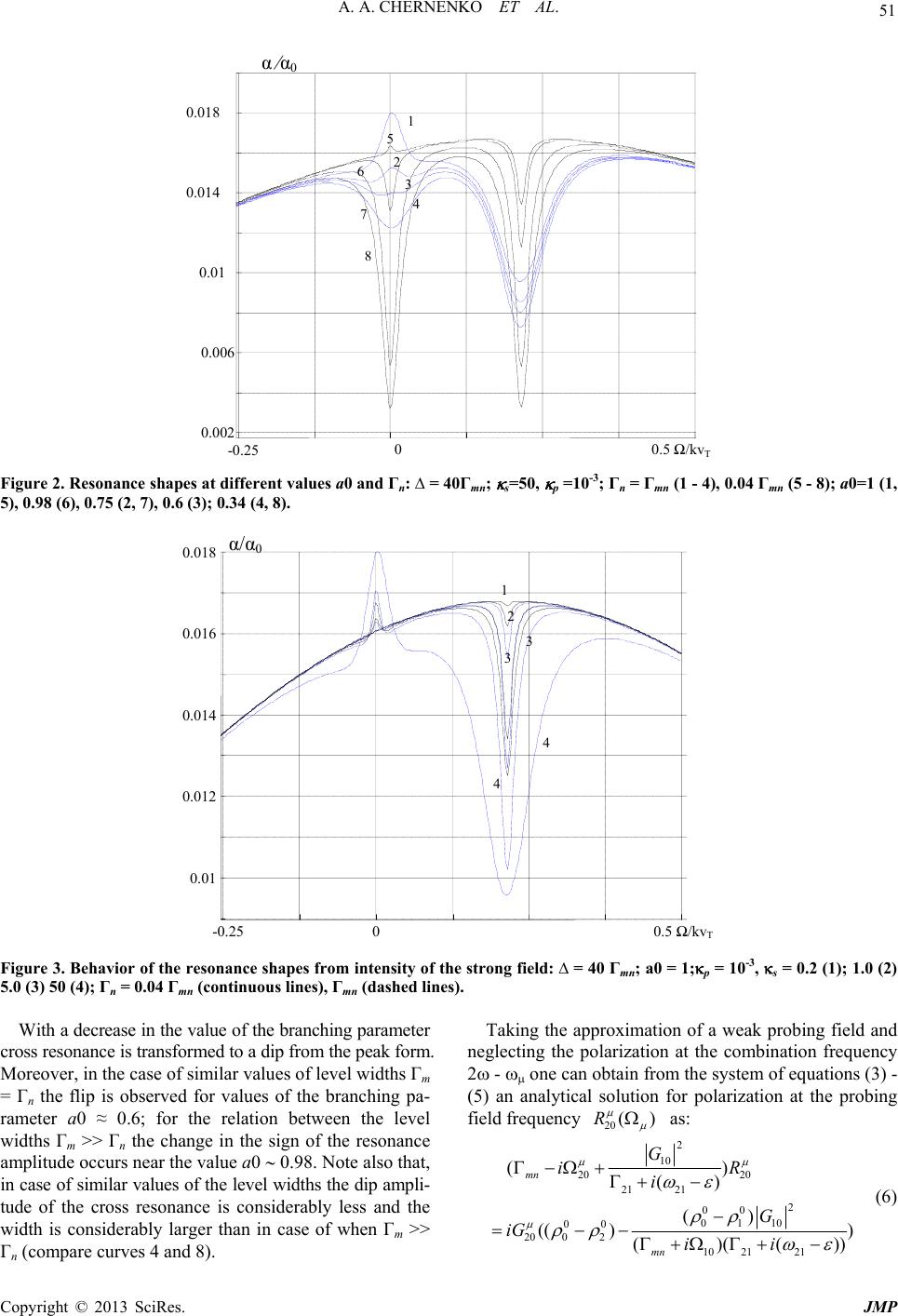 A. A. CHERNENKO ET AL. Copyright © 2013 SciRes. JMP 51 -0.25 00.5 Ω/kv T 0.002 0.006 0.01 0.014 0.018 α ⁄α 0 6 7 8 5 1 2 3 4 Figure 2. Resonance shapes at different values а0 and Γn: ∆ = 40Γmn; s=50, p =10-3; Γn = Γmn (1 - 4), 0.04 Γmn (5 - 8); a0=1 (1, 5), 0.98 (6), 0.75 (2, 7), 0.6 (3); 0.34 (4, 8). -0.25 0 0.5 Ω/kv T 0.01 0.012 0.014 0.016 0.018 α/α 0 1 4 4 3 3 2 Figure 3. Behavior of the resonance shapes from intensity of the strong field: ∆ = 40 Γmn; a0 = 1;p = 10-3, s = 0.2 (1); 1.0 (2) 5.0 (3) 50 (4); Γn = 0.04 Γmn (continuous lines), Γmn (dashed lines). ross resonance is transformed to a dip from the peak form. M Taking the approximation of a weak probing field and neglecting the polarization at the combination frequency polarization at the probing fie With a decrease in the value of the branching parameter c oreover, in the case of similar values of level widths Гm = Гn the flip is observed for values of the branching pa- rameter а0 ≈ 0.6; for the relation between the level widths Гm >> Гn the change in the sign of the resonance amplitude occurs near the value а0 0.98. Note also that, in case of similar values of the level widths the dip ampli- tude of the cross resonance is considerably less and the width is considerably larger than in case of when Гm >> Гn (compare curves 4 and 8). 2 - one can obtain from the system of equations (3) - (5) an analytical solution for ld frequency 20 () R as: 2 10 20 20 21 21 00 () () ( mn G iR i 2 01 10 00 20 02 10 2121 ) (( )) ()(()) mn G iG ii (6)  A. A. CHERNENKO ET AL. 52 Here, the differences of level populations are deter- mined via population of the lower level, branching pa- rameter а0 and rates of stimulated transitions Wik as: 00 0 02 020 00 0 01 010 22 2 00 0 () ; , m ik ns mnmnik W N aW aW (7) 10 20 10 20 (1) ; (1); (1 0)(1 0) 111 m nn mm W W WW where 00 n NQ bsence of the st is the population of the lower level in the arong field. In the velocity (balanced) approximation the presence of a cross resonance is associated with amplitudes of the Bennett dips or peaks in the population of the common level. The specificity of the V-scheme is that the common the lower le vel to the third levels (b shape of form and for the dip. However, the functional rela- tio o- na ilar,1 only the parent resonance will take on the of split- oving atoms. The graphs cor- re level isvel and, in the absence of the sponta- neous radiation from the upper le ranching parameter а0 = 1), a dip in the population of the common level is absent (it follows from (7) that 0 00 N ). It is compensated by the arrival of the spon- taneously emitted particles. In this case the parent reso- nance is caused exclusively by the non-equilibrium population of the upper level. Under these conditions, it follows from solution (6) and averaging over the velocity distribution of particles that the populational part in the the CR (the first summand in solution (6)) is represented by the Doppler contour and the peaks (Fig- ure 2, curves 1 and 5) are caused only by coherent proc- esses (the second summand in (6)), leading to an increase in the absorption coefficient. The performed calculations show that, in the given scheme of transitions, the contri- bution of coherent processes to the CR shape is maximal at equal values of level widths, and for case of Гm >> Гn their contribution is less almost by an order of magnitude. This is illustrated in Figure 2 by the dependences for two relations between values of level widths both for the CR peak shape (curves 1 and 5) and for the dip (curves 4 and 8). The effect of the saturating field intensity on the CR peak shape is shown in Figure 3. Here, for all relations between level widths and any values of the branching parameter, an increase in the strong field intensity leads to an increase in the CR amplitude and width both for the peak n of amplitudes for the peak and for the dip form of the CR in the range of the used intensities of the saturat- ing field appears different. If the CR amplitude in the form of a dip increases by a law close to the square root dependence, the relation of the amplitude of the coherent CR peak under these conditions is of linear character, with the square root dependence for the PR amplitude. Let us mark the character of influence of the probing field intensity: an increase of the probing field intensity results in decreasing in the amplitude of the Doppler lin- ing contour of the absorption line and in the amplitudes of the cross (for the dip and peak shapes) and parent resonances, thus an increase of the widths of these res nces is observed. However, here we did not take into account a capability of appearance of the spectrum fea- tures stipulated by spatial modulation of the nonlinear medium susceptibility in a field of standing waves. These problems were considered earlier (see, for example, ac- tivity [6,7] and reduced links in them). The nonlinear interference effects at the account of saturation by the probing field were calculated also in activity [8], but only for a case of unidirectional waves, in absence of the cross resonances. 3.2. Strong Field of Circular Polarization The case of circular polarizations of the strong and prob- ing wave is of interest. If the signs of rotation of electric field vectors of the strong and probing waves in a me- dium are sim place, its shift in the frequency scale will depend direction of rotation of field vectors and a value ting of the upper levels. In case of the counter circular polarized vectors of fields only a cross resonance will be observed in the ab- sorption line spectrum of the probing wave. The CR is located at the half sum of transition frequencies in the region of the interaction of counter propagating waves with the same group of m sponding to this case are presented in Figure 4. Here the saturated absorption line shapes, calculated for two values of splitting of the upper levels and a number of values of the atomic transition parameters are shown. It is visible, that for any value of level splitting within the limits of the Doppler line width the resonance is exhib- ited on the same light wave frequency. And, in the ab- sence of branching parameter (а0 = 1) resonance is rep- resented as the peak of absorption (curves 1 - 5). As it was marked above, in this case the population part of the CR is absent, and its shape is caused exclusively by the nonlinear coherent process (NIEF agrees with [1]). The presented relations (the most obvious are curves 2 and 4) demonstrate the alternating shape which is typical for the NIEF and a decrease in the effect with an increase in the difference between the level lifetimes. A decrease in the branching parameter а0 leads to appearance of the popu- lational contribution and to transformation of the peak form into a dip (curves 5 - 8). Thus, in case of the counter propagating and counter cir- cular polarized waves the observed resonance of saturated 1In practice, these are experiments in which the probing wave is ob- tained as result of reflection from the mirror behind the cell with a gas. Copyright © 2013 SciRes. JMP  A. A. CHERNENKO ET AL. Copyright © 2013 SciRes. JMP 53 -0.2 -0.1 0 0.1 0.2 Ω⁄ kv T 0.012 0.014 0.016 0.018 0.02 α⁄α 0 4 3 1 8 7 5 6 Figure 4. Shapes of resonances at orthogonally circular polarization of fields: κs = 50; κp =10-3; ∆ = 0 (1, 2), ∆ = 40 Гmn (3-8); a0=1(1-4), 0.9(5), 0.75 (6), 0.6 (7), 0.34 (8); Гn = Гmn (2, 4 – 8), 0.04 Гmn (1, 3). absorption is a cross resonance actually. It is located in e line (in particular, in absence of splitting) and has between st scopy and Its Application Program (project 9.5) of the Branc Physical Sciences, Russian Academences. REFERENCES [1] S. G. Rautian, G. I. Smirnov and A. M. Shalagin, Spectra of Atoms and Mole- , 1979, [in Russian]. vel Λ- and V- Systems,” Optics of Atmosphere and Ocean, Vol. 16, No. 7, 200 [4] E. G. Saprykid A. M. Shalagin, opy,” Optics and Spectroscopy, Vol. 2 y of Sci the center of the unshifted transition line at any value of splitting of the upper levels within the Doppler width of th under certain conditions extremely coherent nature. Ac- cording to the results of [1], interference phenomena in the case of counter propagating waves that are absent in the approximation of first nonlinear corrections can ap- pear in the next order with respect to saturation. This fact explains the aforementioned linear character of the in- crease of the coherent CR amplitude in Figure 2 with the square rooted dependence of the PR amplitude. In conclusion we shall indicate on a capability of ex- perimental observation of the coherent type saturated absorption resonance. The given resonance will be real- ized only in the V-type of transitions in atoms “Nonlinear Resonances in cules,” Nauka, Novosibirsk [2] V. S. Letokhov and V. P. Chebotayev, “Nonlinear Laser Spectroscopy of Ultrahigh Resolution,” Nauka, Moscow, 1990. [in Russian]. [3] Yu. V. Bogdanova, “Nonlinear Resonances in the Signals of Magnetic and Frequency Scanning of Three-le 3, pp. 567-575. n, A. A. Chernenko an “Effect of the Atomic Transition Parameters on Cross Resonance Shapes in Spectroscopy of Probing Field,” Iz- vestiya Vuzov. Fizika, No. 2/2, 2011, pp. 255-268. [5] E. G. Saprykin, A. A. Chernenko and A. M. Shalagin, “On the Shape of Cross Resonances in Counterpropagat- ing Wave Spectrosc ates with the full moments J = 0 and J = 1, thus the up- per state of transition should breaks up mainly on the lower state to supply the value of branching parameter a0 ~ 1. Transitions 1S0 – 1,3P1 from the ground state of the alkaline-earth metal atoms, and of the Hg, Cd, Zn and Yb atoms satisfy to these requirements. The wave lengths of these transitions are located in spectral area of generation of existing power tunable lasers (in the visible range), or their second harmonics (in the UV range). 4. Acknowledgements This work was supported by the NSh-2979.2012.2 pro- ject and the Fundamental Optical Spectro 113, No. 5, 2012, pp. 585-597. doi:10.1134/S0030400X12080152 [6] M. G. Stepanov, “Autler-Townes Doublet Probed by Strong Field,” Journal of Physycs B: Atomic, Molecular nce,” nd All-Optical Switch- usly Brodened Me- and Optical Physics, Vol. 32, 1999, pp. 649-661. [7] S. A. Babin, E. V. Podivilov, V. V. Potapov, D. V. Churkin, and D. A. Shapiro,” Nonlinear Resonance, In- duced by Maximum Spatial Harmonics of Cohere Journal of Experimental and Theoretical Physics, Vol. 121, No. 4, 2002, pp. 807- 818. [8] A. K. Popov, S. A. Myslivets and Tomas, F. Geoges, “Nonlinear Interference Effects a ing to Optically Dense Inhomogeneo dia” Physical Review A, Vol. 71, 2005. h of |

