 Journal of Modern Physics, 2013, 4, 18-22 doi:10.4236/jmp.2013.45B004 Published Online May 2013 (http://www.scirp.org/journal/jmp) Stability and Vorticity Production in Stratified Astrophysical Disks E. S. Uchava1,2,3, A. G. Tevzadze1, G. D. Chagelishvili1,2,3 1Department of Physics, Faculty of Exact and Natural Sciences, Tbilisi State University, Tbilisi, Georgia 2E. Kharadze Abastumani Astrophysical Observatory, Ilia State University, Tbilisi, Georgia 3M. Nodia Institute of Geophysics, Tbilisi State University, Tbilisi, Georgia Email: aleko@tevza.org Received 2013 ABSTRACT We study local linear non-axisymmetric perturbations in fully stratified 3D astrophysical disks. Radial stratification is set to be described by power law, while vertical stratification is set to be exponential. We analyze the linear perturba- tions in local shearing sheet frame and derive WKB dispersion equation. We show that stratification laws of the disk matter define not only the thermal stability of the disk, but also the efficiency of the potential vorticity production by rotationg convective turbulence in astrophysical disks. Taken developed convective turbulence we assume nonlinear tendencies set by linear spectrum and show that vortices are unlikely to be generated in rigid rotatio n flows. In con trast, differential rotation yields much higher vortex production rate that depends on the disk thickness, distance from the central object and the spectral characteristics of the developed thermal turbulence. It seems that measurements of the temperature and density distribution in accretion disks may indicate the efficiency of the turbulence development and largely define the luminosity characteristic of accreting flows. Keywords: Accretion Disks; Protoplanetary Disks; Turbulence 1. Introduction Stability and turbu lence in hydrodynamic accretion disks are often considered as a key phenomena in defining the anomalous viscosity and corresponding accretion rate in high energy accretion disks [1,2], as well as in the proc- ess of planet formation in the core accretion model in protoplanet ary disks [3- 6] . In presented research note we give non-axisymmetric local linear WKB stability analysis of differentially ro- tating fully stratified astro physical disks and describe the possibility of po tential vorticity g eneration. We speculate on the nonlinear developments of the convective turbu- lence and what will be the consequencies for the vortex production in such flows. The horizontal component of the potential vorticity is thought to be most important in protoplanetary disks for core accretion modes. In this respect we show that hori- zontal vortices can only be generated from vertical vor- ticity if no shear is present. We anticipate the spectral characteristic of the convective turbulence in differenc- tially rotating flows base on the growth rates of thermal nstability. Thus, we are able to estimate the polarity of the vortices produced in stratified astrophysical flows. In Sec. 2 we give mathematical formalism of the con- sidered physical model. We introduce linear perturba- tions and derive rigid rotation as well as WKB spectum for differentially rotating flows. We demonstrate th e pos- sibility of vortex production in stratified flows. The findings are shortly discussed and the paper is summa- rized in Sec. 3. 2. Physical Model Let us consider the Boussinesq flow rotating around a central gravitating object under the influence of radial and vertical stratification in cylindrical co-ordinates: 21 () rr V VV P trr V, r g (1) 1 () r VV VV trr V, P (2) 1 () , z VV P tz Vz g (3) () 0SS t , V (4) () rz V. Vf fVf rr z V (6) Copyright © 2013 SciRes. JMP  E. S. UCHAVA ET AL. 19 We consider equilibrium state of the disk with radial power law and vertical exponential stratification: 00 (,)exp , P r PzrP rH z (7) 00 (,)exp , r zr rH z (8) 00 (,)exp( 1), S rz SzrS rH (9) where P, and S indices describe the radial structure of the disk, H is the vertical stratification length-scale, while parameter describes the vertical structure. Note that here differs from standard adiabatic index and can have values less than unity. In this case the direction of the entropy stratification is reversed. We keep the value of general aiming to mimic the different heating and cooling properties of the disk (not explicitly consid- ered in this paper). In the thin disk approximation we consider radial and vertical gravitational acceleration constant over disk height: 2 , , rz GM GMH gg rr 3 (10) where G is the gravitational constant and M is the mass of central gravitating object. In the equilibrium we con- sider azimuthal flow V0 = (0, r , 0). Hence, introduc- ing Keplerian angular velocity: 3 22 0 30 () , KGM r rr r (11) we may derive the system parameters in equilibrium: 2 2 200 02 00 ,, P PC CH 3, (12) with quasi-Keplerian angular velocity: 22 22 00 () ()1. KP Hr rr rr (13) Eqs. (7)- (9) set an equilibrium disk model that is baro- clinic in nature: 0P . In the case of proto- planetary disks when pressure normally decreases with radius ( P > 0 ) Equation (13) indicates sub-Keplerian equilibrium flow (). 2.1. Linear Perturbations We employ Boussinesq approximation where the change of density is due to thermal effects and compressibility is neglected. Equations governing the dynamics of linear perturbations are inhomogeneous in space due to several distinctive factors. Among these we can distinguish ra- dial and vertical stratification of the disk matter, radial inhomogeneity of the angular velocity and global curva- ture of the flow. In order to simplify linear analysis we can deal with these complications separately. We use local shearing sheet analysis, which is designed to deal with the latter factor: flow curvature. To deal with back- ground inhomogeneities due to fully stratified state we re-scale linear perturbations in global frame in such a way to remove explicit coordinate dependence in local frame (see the 2D analog in [7]). Hence, we split physi- cal variables into the background components and linear perturbations as follows: 0 00 (,)(,)/ (,), (,)()(,)/ (,), (,)(,)/ (,), (,) (,)(,), (,) (,)(,), (,) (,)exp(,). S rr zz VtVt rz VtrrVt rz VtVt rz PtPrzP t trz t Srz St SrzS t rH rr rr rr rr rr rr (14) Note the specific scalling factors for the perturbations of velocity and entropy. Using local shearing sheet frame that co-rotates with the disk flow at r = r0 radius: 000 , (). rr yrrt (15) we neglect the flow curvature and study effects of the differential rotation in the form of th e uniform shear flow. Hence, the angular velocity of th e rotation is reduced to 00 ()( )2. rrA r (16) where the Oort's parameters are defined as follows: 2 2 0 00 35 1. 4() 3 PH Arr (17) Now we can employ Fourier expansion of linear per- turbations in space with time varying phase: (,) (,) (,) (,) exp( ) (,) (,) (,) (,) (,) (,) xx xy yy zz Pt ipt Vtu t iktxikyik z Vtu t Vtu t St st rk rk rk rk rk z where: ()(0) 2 x kt kAkt y (18) and the following characteristic wavenumbers are intro- duced: 000 1 , , , . SP RSPH kkkk rrr H Copyright © 2013 SciRes. JMP  E. S. UCHAVA ET AL. 20 Hence, the system governing the linear dynamics of perturbations in the limit 22 H kk is reduced to the following: 2 0 0 2() P xyx kC duuktp s dt 0, (19) 2 yxy duBukp dt 0, (20) 2 00, H zz kC dukp s dt (21) (1 )0, sx Hz dskuku dt (22) () 0. xxyyzz ktu kuku (23) Similar system in Boussinesq limit has been already derived for Lagnrangian perturbations to study the mo- mentum transport by linear perturbations in fully strati- fied disks [6]. In present note we focus on the vorticity production and stratistical properties of nonlinear turbu- lent state developed due to thermal instability. The linear perturbations of potential vorticity that can be also derived from Ertel's theorem is the following: (,) (1) 2 . (1) S yyx zyyz H z H k Wtkuku kuku k Bk s k k (24) In the considered stratified flow potential vorticity production is described by the following linear equation: 2 0 2 (,) (,). 1 S yP H k dW tkks t dt k kk (25) Dynamics of vorticity is defined by potential vorticity perturbations, that is system invariant in barotropic flows (kP = kS = 0). 2.2. Rigid Rotation Spectrum Dispersion equation can be derived straightforwardly in the case of rigid body rotation, i.e. zero shear limit in local frame (A=0, B = -0). In this case dispersion equa- tion is derived using Fourier expansion of spatial har- monics in time (see Eqs. (19) - (23). Hence, the disper- sion equation reads as fo llows: 22 000 () giDi 0, (26) where 2 22 22 022 2 02 4 (1) , x is the frequency of density-spiral waves in stably strati- fied flows , 3 0 02 2(1) yz PS H kk kk kk , 2 (28) 22222 , , yzz xy kkkkkk and 22 2 00 2,(1) PS rz H kk nn k 2 . (29) Stability of the linear perturbations in this case is de- fined by parameter and is consistent with the axisym- metric stability criterion derived in [8]: = 0. Otherwise, instability is set by > 0 and exponential damping by < 0. 2.3. Non-axisymmetric WKB Spectrum Within WKB approximation we assume that 2 ()() (),()(). dd titttt dt dt (30) Applying ansatz (30) into Eqs. (19-23) we derive the WKB local dispersion equation of linear perturbations in the stratified differentially rotating disk flows: 2 0 2 20 xy kk DiA i k 1 , (31) where 2 0 10 2 2( 1). yPz Hx H k kk kk kk (32) Figrue 1 shows numerical values of the WKB growth rates in fully stratified accretion disk flow with sub-Ke- plerian differential rotation, weak radial and unstable (< 1) vertical stratification laws. Figure shows asym- metry of the instability, when strongest growth occurs for linear modes with . 0 xy kk 3. Discussion and Summary We have studied 3D stratified hydrodynamics accretion disks in local shearing sh eet approx imation. We drive the stability characteristics, as well as conditions for the generation of linear perturbations of potential vorticity. Thermal instability that developes into the convective /buoyant turbulence tend s to modify the stratification law of thermal instability in a way to minimize its linear growth rate. In our case rigid rotation spectrumwill yield: =0 (see Eq. (26)). In this limit perturbations of the potential vorticity can not be generated (see Equation (25)): 2 2 z grz Sxz H k kk Bnn kk k kkkk kk (27) (,) .Wtconstk On the other hand the vertical and horizontal compo- Copyright © 2013 SciRes. JMP 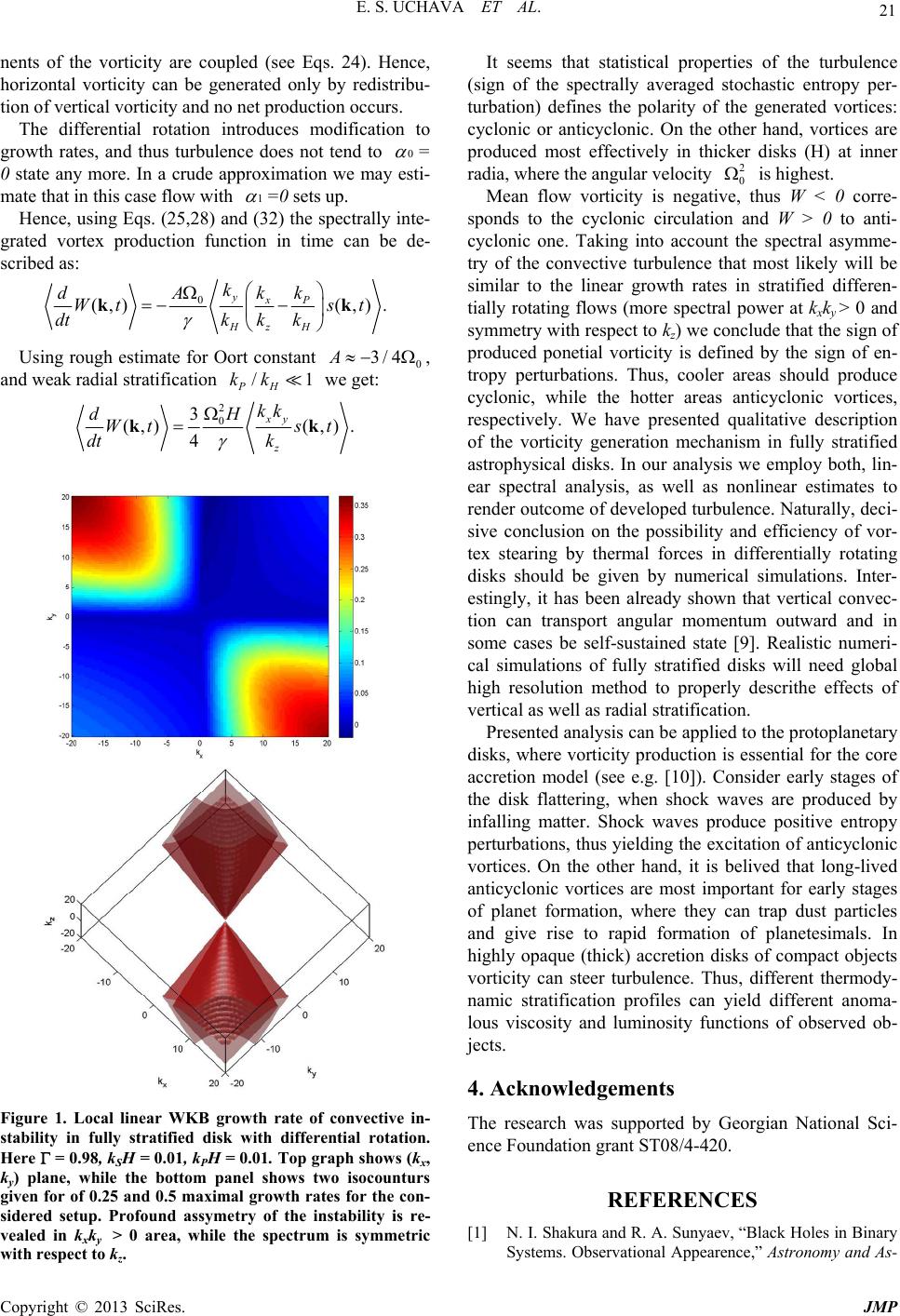 E. S. UCHAVA ET AL. 21 nents of the vorticity are coupled (see Eqs. 24). Hence, horizontal vorticity can be generated only by redistribu- tion of vertical vorticity and no net production occurs. The differential rotation introduces modification to growth rates, and thus turbulence does not tend to 0 = 0 state any more. In a crude approximation we may esti- mate that in this case flow with 1 =0 sets up. Hence, using Eqs. (25,28) and (32) the spectrally inte- grated vortex production function in time can be de- scribed as: 0 (,) (,). yxP Hz H k Ak k dWt st dtk k k kk Using rough estimate for Oort constant , and weak radial stratification we get: 0 3/4A 1/ PH kk 2 0 3 (,) (,). 4 xy z kk H dWt st dt k kk Figure 1. Local linear WKB growth rate of convective in- stability in fully stratified disk with differential rotation. Here = 0.98, kSH = 0.01, kPH = 0.01. Top graph shows ( kx, ky) plane, while the bottom panel shows two isocounturs given for of 0.25 and 0.5 maximal growth rates for the con- sidered setup. Profound assymetry of the instability is re- vealed in kxky > 0 area, while the spectrum is symmetric with respect to kz. It seems that statistical properties of the turbulence (sign of the spectrally averaged stochastic entropy per- turbation) defines the polarity of the generated vortices: cyclonic or anticyclonic. On the other hand, vortices are produced most effectively in thicker disks (H) at inner radia, where the angular velocity is highest. 2 0 Mean flow vorticity is negative, thus W < 0 corre- sponds to the cyclonic circulation and W > 0 to anti- cyclonic one. Taking into account the spectral asymme- try of the convective turbulence that most likely will be similar to the linear growth rates in stratified differen- tially rotating flows (more spectral power at kxky > 0 and symmetry with respect to kz) we conclude that the sign of produced ponetial vorticity is defined by the sign of en- tropy perturbations. Thus, cooler areas should produce cyclonic, while the hotter areas anticyclonic vortices, respectively. We have presented qualitative description of the vorticity generation mechanism in fully stratified astrophysical disks. In our analysis we employ both, lin- ear spectral analysis, as well as nonlinear estimates to render outcome of developed turbulence. Naturally, deci- sive conclusion on the possibility and efficiency of vor- tex stearing by thermal forces in differentially rotating disks should be given by numerical simulations. Inter- estingly, it has been already shown that vertical convec- tion can transport angular momentum outward and in some cases be self-sustained state [9]. Realistic numeri- cal simulations of fully stratified disks will need global high resolution method to properly descrithe effects of vertical as well as radial stratification. Presented analysis can be applied to the protoplanetary disks, where vorticity productio n is essential for the core accretion model (see e.g. [10]). Consider early stages of the disk flattering, when shock waves are produced by infalling matter. Shock waves produce positive entropy perturbations, thus yielding the excitation of anticyclonic vortices. On the other hand, it is belived that long-lived anticyclonic vortices are most important for early stages of planet formation, where they can trap dust particles and give rise to rapid formation of planetesimals. In highly opaque (thick) accretion disks of compact objects vorticity can steer turbulence. Thus, different thermody- namic stratification profiles can yield different anoma- lous viscosity and luminosity functions of observed ob- jects. 4. Acknowledgements The research was supported by Georgian National Sci- ence Foundation grant ST08/4-420. REFERENCES [1] N. I. Shakura and R. A. Sunyaev, “Black Holes in Binary Systems. Observational Appearence,” Astronomy and As- Copyright © 2013 SciRes. JMP  E. S. UCHAVA ET AL. Copyright © 2013 SciRes. JMP 22 trophysics, Vol. 24, 1973, pp. 337-355. [2] G. D. Chagelishvili, J.-P. Zahn, A. G. Tevzadze and J. G. Lominadze, “On Hydrodynamical Shear Turbulence in Keplerian Flows: Via Transient Growth to Bypass Tran- sition,” Astronomy and Astrophysics, Vol. 402, 2003, pp. 401-407. doi:10.1051/0004-6361:20030269 [3] P. Armitage, “Dynamics of Protoplanetary Disks,” An- nual Review of Astronomy and Astrophysics, Vol. 49, No. 1, 2001, pp. 195-236. doi:10.1146/annurev-astro-081710-102521 [4] G. Bodo, A. G. Tevzadze, G. D. Chagelishvili, A. Mi- gnone, P. Rossi and A. Ferrari, “Stability and Nonlinear Adjustment of Vortices in Keplerian Flows,” Astronomy and Astrophysics, Vol. 475, No. 1, 2007, pp. 51-61. doi:10.1051/0004-6361:20077695 [5] G. Bodo, G. D. Chagelishvili, G. Murante, A. G. Tevzadze, P. Rossi and A. Ferrari, “Spiral Density Wave Generation by Vortices in Keplerian Flows,” As- tronomy and Astrophysics, Vol. 437, No. 1, 2005, pp. 9-22. doi:10.1051/0004-6361:20041046 [6] F. Volponi, “Linear Transport in Fully Stratified Disks,” Monthly Notice of the Royal Astronomical Society, Vol. 406, No. 1, 2010, pp. 551-557. doi:10.1111/j.1365-2966.2010.16688.x [7] A. G. Tevzadze, G. D. Chagelishvili, G. Bodo and P. Rossi, “Linear Coupling of Modes in Two-Dimensional Radially Stratified Astrophysical Disks,” Monthly Notice of the Royal Astronomical Society, Vol. 401, No. 2, 2010, pp. 901-912. doi:10.1111/j.1365-2966.2009.15723.x [8] G. Rudiger, R. Artl and D. Shalybkov, “Hydrodynamic Stability in Accretion Disks Under the Combined Influ- ence of Shear and Density Stratification,” Astronomy and Astrophysics, Vol. 391, No. 2, 2002, pp. 781-787. doi:10.1051/0004-6361:20020853 [9] G. Lesur and G. Ogilvie, “On the Angular Momentum Transport Due to Vertical Convection in Accretion Discs,” Monthly Notice of the Royal Astronomical Society, Vol. 404, No. 1, 2010, pp. L64-L68. doi:10.1111/j.1745-3933.2010.00836.x [10] A. G. Tevzadze, G. D. Chagelishvili and J.-P. Zhan, “Hydrodynamic Stability an Mode Coupling in Ke- plerian Flows: Local Strato-Rotational Analysis,” Astronomy and Astroph ysics , Vo l. 478 , No . 1 , 20 08, pp. 9-15. doi:10.1051/0004-6361:20078386
|