Paper Menu >>
Journal Menu >>
 Natural Resources, 2010, 1, 80-87 doi:10.4236/nr.2010.12008 Published Online December 2010 (http://www.SciRP.org/journal/nr) Copyright © 2010 SciRes. NR Detection on Resources Consumption Drag of Urbanization in China Yaobin Liu1,2,3, Guixin Wang2, Shuming Bao3 1Research Center for the Central China Economic Development, Nanchang University, Nanchang, China; 2State Innovative Institute for Public Management and Public Policy, Fudan University, Shanghai, China; 3China Data Ceter, The University of Michigan, Ann Arbor, USA. Email: liuyaobin2003@163.com Received October 29th, 2010; revised November 25th, 2010; accepted November 26th, 2010. ABSTRACT A unique model of resources consumption drag of urbanization is developed by employing the neo-classical production model and the urbanization relation model. By using this model, it is viable to estimate the resources consumption drag, measured as the reduced speed of urbanization from resources consumption and environmental services. In terms of reduced urbanization process, the aggregated and disaggregated effects from some crucial resources, such as energy, land and water, are calculated and presented. The results show that the drags from energy consumption, land and wa- ter in process of China’s urbanization are 0.1061, 0.0036 and 0.1914 percent point respectively and the aggregate drag arrives 0.3010 percent point. With the increasing population and the developing urbanization process in China, the constraints of resources, water and energy in particular cannot be eliminated and the drags will be enhanced and hence the pressure of further urbanization process is still a relatively serious problem. Keywords: Urbanization, Rresources Consumption Drag, Economic Growth Model, Urbanization Relation Model 1. Introduction Natural resources, pollution, and other environmental considerations are absent from the Solow model [1]. However, since Malthus made his classic argument, many people started to believe these considerations are critical to the possibilities of long-run economic growth [2]. For example, the amount of oil and other natural resources on earth are fixed. This could mean that any attempt to seek a perpetually rising output will eventually deplete those resources, and such move will therefore fail. Similarly, the fixed supply of land may become a blinding con- straint on our ability to produce [3]. Increasing output may generate an ever increasing stock of pollution that will suspend the exploitation growth. How do natural resources and environmental limitations affect long-run growth? Without the existence of property rights of the notably natural resources, land and those for which there are not notably pollution-free air and water, it will be an important constraint on future production. Therefore, it is becoming increasingly appropriate to view the economic system as a growing subsystem within the ecological system instead of an independent one with more or less infinite access to input and output. The cost of environ- mental constraints on welfare is labeled the environ- mental drag [4]. The overall environmental drag can af- fect economic growth and total welfare in different pro- portions. Earlier economic studies have provided valu- able theoretical contributions to the understanding of how the environment constrains economic development. For instance, Dasgupta and Heal showed that when tak- ing account of a drag from nonrenewable resources, a steady state growth path only existed when the nonre- newable resource was essential in production [5]. Nord- haus made use of the expanded Cobb-Douglas function as a tool to estimate the growth drag constrained by re- sources and land in the U.S. He argued that the value was 0.0024 [6]. Tahvonen and Kuuluvainen showed that a steady state economic development path with pollution was only possible in the case of a relatively low discount rate [7]. Xue et al. studied the drag of economic growth because of land constraints in China. The calculated re- sult of the drag was about 0.0175 per year [8]. Xie et al. estimated the drag of economic growth because of land and water constraints in China, and they found that the drags from the water and land were 0.0014 and 0.0132 respectively, and the aggregate drag was 0.0146 [9].  Detection on Resources Consumption Drag of Urbanization in China Copyright © 2010 SciRes. NR 81 Urbanization is perhaps one of the most important human activities in recent years all around the world [10]. However, this situation is heterogeneous all around the globe [11]. Rapid urbanization is often the cause of enormous pressure on rural and natural environment. One the one hand, continuous aggregation of urban popula- tion has largely contributed the increase of the natural resources such as water, land, energy, and mineral re- sources [12]. On the other hand, urbanization process has been restricted due to scarcity of natural resource and environmental pollution. Obviously, there is a tight rela- tionship among exploitation and utilization of natural resource & environment and urbanization, ant it can be depicted in the climbing slope model of urbanization [13]. As shown in Figure 1, during the ascending process of urbanization, the socio-economic system has its own gravitation (G). Correspondingly, the natural resources and environmental system gives a holding power (N) to it. In the direction which urbanization moves forward, a driving force (F) and a resisting force (f) exist. The driv- ing force includes the pulling force from the demand of urbanization and the pushing force from the supply out- side; the resisting force is the friction between the ur- banization system, the natural resources system, and the environmental system, which can be expressed by the arithmetic product of the holding power (N) and the fric- tion coefficient (u). The above forces are all composite forces. During a certain period and in a certain area, if natural resources are the shorter, the maximum of the holding power (N) will be mainly decided by the natural resources carrying capacity (NRCC). On the other hand, the pressure which urbanization system places on natural resources system is tremendous when compared with the resources carrying capacity, while the pressures that ur- banization system gives to other resources system is small when compared with other natural resources car- rying capacity. Consequently, we can consider that the friction resources system gives to the urbanization sys- tem is by far the largest and the friction that other re- sources system gives to the urbanization system is near zero. Subsequently, the resisting force on urbanization is mainly decided by the NRCF. Therefore, to accelerate Figure 1. Climbing slope model of urbanization. the urbanization process and realize the sustainable utili- zation of natural resources, quantitative method and em- pirical study on the resource consumption the drag of urbanization should be constructed and perfected. China has witnessed fast urban growth over the past decades. From 1978 to 2008, the number of cities in- creased from 193 to 661. The number of towns with ad- ministrative systems increased from 2,173 to 19,369 during the same period. The total urban population jumped from 170 million to 577 million and the percent- age of urban population went up from 17.9% to 45.68%. Especially in the 1990s, China experienced a rapid ur- banization. As urbanization is still in process, it will be inevitably accompanied by dramatic increases in the consumption of water, land, energy and mineral re- sources. Domestic water demand due to growth and liv- ing standards has gradually led to a shortage of water in China [14]. Water crises occurred in over 400 Chinese cities in 2000, and in Northern China water consumption of each person has dropped to half of that in Egypt [15]. Varis and Vakkilainen identified great water-related challenges in the coming decades [16], and Ren et al. revealed that rapid urbanization corresponded with fast degradation of water quality [17]. The processes of agri- cultural restructuring, rural industrialization and rapid urbanization in China since the 1990s have led to a new trend of massive farmland loss for the benefits of market farming and non-agricultural developments. To explore the impact of natural resources on urbanization, it is nec- essary to take land, water and energy as crucial natural resources, to calculate the resource consumption drag in China’s urbanization. 2. Theoretical Models 2.1. Neo-Classical Production Model To investigate the effects from natural resources since economic growth, we used the framework proposed by Romer [3]. The framework is based on the neo-classical production model where capital, labor, energy, land and water resource are treated as the separate inputs [8-9]. That is: 1- - Y = KRTWAL, 0, 0, 0, 0, +1 ttttttt (1) where Y is aggregate output; K is the capital stock; L is the amount of labor; R is the amount of energy; T is the utilized amount of land, W is water resources used in production. The constant parameters , , and are the output elasticity with respect to capital, energy, land and water natural resource, respectively. The dynamics of ca-  Detection on Resources Consumption Drag of Urbanization in China Copyright © 2010 SciRes. NR 82 pital, labor and the effectiveness of labor (() () A tLt ) are the same as Solow model [1]. Taking logs of both sides of Equation (1), and we have: lnlnln ln ln 1lnln YtKtRt Tt Wt At Lt (2) Considering the time derivative of the log of a variable equals the variable’s growth rate, we can obtain: 1 YKRTW g tgtgtgtg gn (3) where gY is the growth rate of Y(t). The growth rates of K(t), R(t), T(t), W(t), A(t) and L(t)and are gK(t), gR(t), gT(t), gW(t), g and n, respectively. According the neo-classical growth theory, gY and gK will be equal if the economy is on a balanced-growth- path. We have: 1 1 RTW bgp y g gg gn g (4) where bgp Y g denotes the growth rate of Y on the balanced growth path. We can immediately determine whether the economy converges to this balanced-growth-path. As Equation (4) shows, gK converges to its balanced-growth- path value and the economy converges to its balanced growth path. Therefore, the growth rate of output per worker on the balanced-growth-path is: / 1 1 Y bgp L bgp bgp YL RTW g gg g ggg n (5) Equation (5) shows that growth in income per worker on the balanced-growth-path / bgp YL g can be either positive or negative. That is, natural resource and land limitations can eventually cause output per worker to be falling and they do not. In fact, the declining quantities of resource and land per worker are drags on growth. However, technological progress is a spur on growth. If the spur is larger than the drags there will be a sustained growth in output per worker. This is precisely what has happened over the past centuries. 2.2. Urbanization Relation Model Rapid economic growth accompanies rapid industrializa- tion and urbanization. Such prominent growth, in the form of a radical intersectional and interregional reallo- cation of resources, has been triggered by integrations in factor and goods markets [18]. There is an existence of economic growth drag induced from natural resources. We establish the linkage between urbanization and eco- nomic growth and hence can further detect the resources consumption of urbanization. Urbanization has tradition- ally associated with economic development, and eco- nomic growth and urbanization are inextricably linked. The resources consumption of urbanization can be de- duced by the relation model between urbanization and economic growth. Denote u and y as urbanization rate and per capita output for the overall country, respectively. The proce- dure can be seen by the following: 1 uu rr ur ur yP yP yuyuy PP (6) where u P andr P are urban population and rural popu- lation; u y u y and r y are per capita output for the urban population and rural population; u z and r z are is labor productivity for the two sectors; u v and r v are the social maintenance indexes for the two sectors (the ratio of total population to labors). Assume that u y is greater than r y, and the propor- tion of u y and r y to y is a constant . That is to say 1 ur uyuyy . Then, Equation (7) can be derived as follows: 1 ur yy dy du (7) According to the urban-rural equilibrium model [19], it is feasible to assume ur yyky [20]. k is a constant , then we have: 1 dyk du y (8) To solve Equation (8), the urbanization relation model can be obtained: = + ln(0,0)uabya b (9) where u is urbanization level; y is per capita output; a, b is the coefficients respectively. In order to do a connec- tion with Equation (5), we take the exponential model to deal with Equation (9) and have: u y = e,0,0e (10) where is the elasticity value; and are the coefficients respectively. 2.3. Resources Consumption Drag Model of Urbanization The new assumptions concern the other natural resources and land. With the fixed amount of land and water re- source on earth, in the long run the quantity used in pro-  Detection on Resources Consumption Drag of Urbanization in China Copyright © 2010 SciRes. NR 83 duction cannot increase and hence we assume () 0Tt and () 0Wt . Similarly, the energy endowments are fixed and the resources used in production imply that the energy use will eventually decline. Even though energy use has been rising historically, we yet assume ()(), 0RtbRt b . The presence of the energy, land and water in the production function means that K/AL no longer converges to some value. As a result, we cannot use the previous approach of focusing on K/AL to ana- lyze the behavior of this economy. By dropping the nat- ural resource use per worker and land per worker, energy, land and water limitations have a reducing growth. However, Nordhaus observes how much greater growth would be if natural resources per worker were constant [6]. Concretely, we assume an economy the same as the above one we have just discussed, and the assump- tion () 0Tt , () 0Wt and () ()Rt bRt are replaced with the assumption () ()Tt nTt , ()()Wt nWt and () ()Rt nRt . In this hypothetical economy, energy, land and water limitations increase with a growing population. Analysis parallels the results of Equation (5) and shows the growth of output per worker on the balanced- growth-path in this economy is: / 11 1 bgp YL Rt nRtgg (11) The “growth drag” from natural resource limitations is the difference between growth in this hypothetical case and growth in the case of the natural resource limitations: // 1 bgp bgp YL YL bn Drag gg (12) Thus, the growth drag is increasing associated with energy share(β), land share(γ) , water share(), and the rate of energy uses is falling(b), as well as the labor growth rate (n) and capital share(α). With Equation (7) and Equation (5), we can achieve the condition when urbanization converges to its bal- anced-growth-path. This is: 1 1 RTW g ggg n u (13) where u is the growth rate of urbanization level; λ is the elasticity of urbanization to per capita output1. Similarly, we achieve to obtain a unique resources consumption drag model of urbanization where the impacts from en- ergy, land and water consumption during urbanization process respectively is: 1 u R n Drag , 1 u T n Drag and 1 u W n Drag . Correspondingly, the aggregate drag can be indicated as 1 u RTW n Drag . The model suggests that with natural resources limita- tions the reduction in urbanization process exists but not prominent. In urbanization process, the aggregate drag positively relates with energy production elasticity (β), land production elasticity (γ), water production elasticity (θ) and labor growth rate (n) as well as the capital pro- duction elasticity (α), respectively. It increases with the coefficients, but decrease with the elasticity of urbaniza- tion to per capita output (λ). 3. Detection Results 3.1. Variables and Data Discussion 3.1.1. Date and Unit Root Test The study is based on annual data over a period from 1978 to 2008 in China. All the time series data of utilized land(T), available water resource (W), energy consump- tion (R), GDP (Y), Labor (L), capital stock (L) and the urbanization rate (u, percentage of urban population in total population) are from National Statistic Yearbook 2009 [21], Statistical issue of New China during Fifty Years [22], National Environment Bulletin [23], Energy Statistic Yearbook [24] and http://www.cei.gov.cn In order to have comprehensive results, a unit root test, namely augmented Dickey–Fuller (ADF) is done in ad- vance to test the smooth characteristics of the variables. To conserve space, the details of the unit root test here do not be further discussed [25]. ADF test is often criticized due to its low power properties [26]. However, it is still take it into account for its high frequency in most of rela- tive studies. It is well known that the unit root test is sen- sitive to different lag structures. Hence, a lag selection as information criteria is employed [27], namely Schwarz Information Criterion (SIC), which is also often used in relative studies. The unit root test in the study has a null hypothesis that the series has a unit root against the al- ternative of stationarity. The result show that all null hy- potheses are unit root, in which the result indicates that all the variables are non-stationarity in their level data (with or without trend). However, the stationarity prop- 3In economics, elasticity is the ratio of the percent change in one vari- able to the percent change in another variable. It is a tool for measuring the responsiveness of a function to changes in parameters in a relative way. Because urbanization level itself is a relative parameter, the ex- p ression employed in the paper is no the same as the general one. How- ever, in this particular issue, the above expression can also be inter- p reted as one of elasticity. In addition, λ indicates that the change of pe r capita output to the percent change of urbanization level, along with the other conditions unchan g ed. 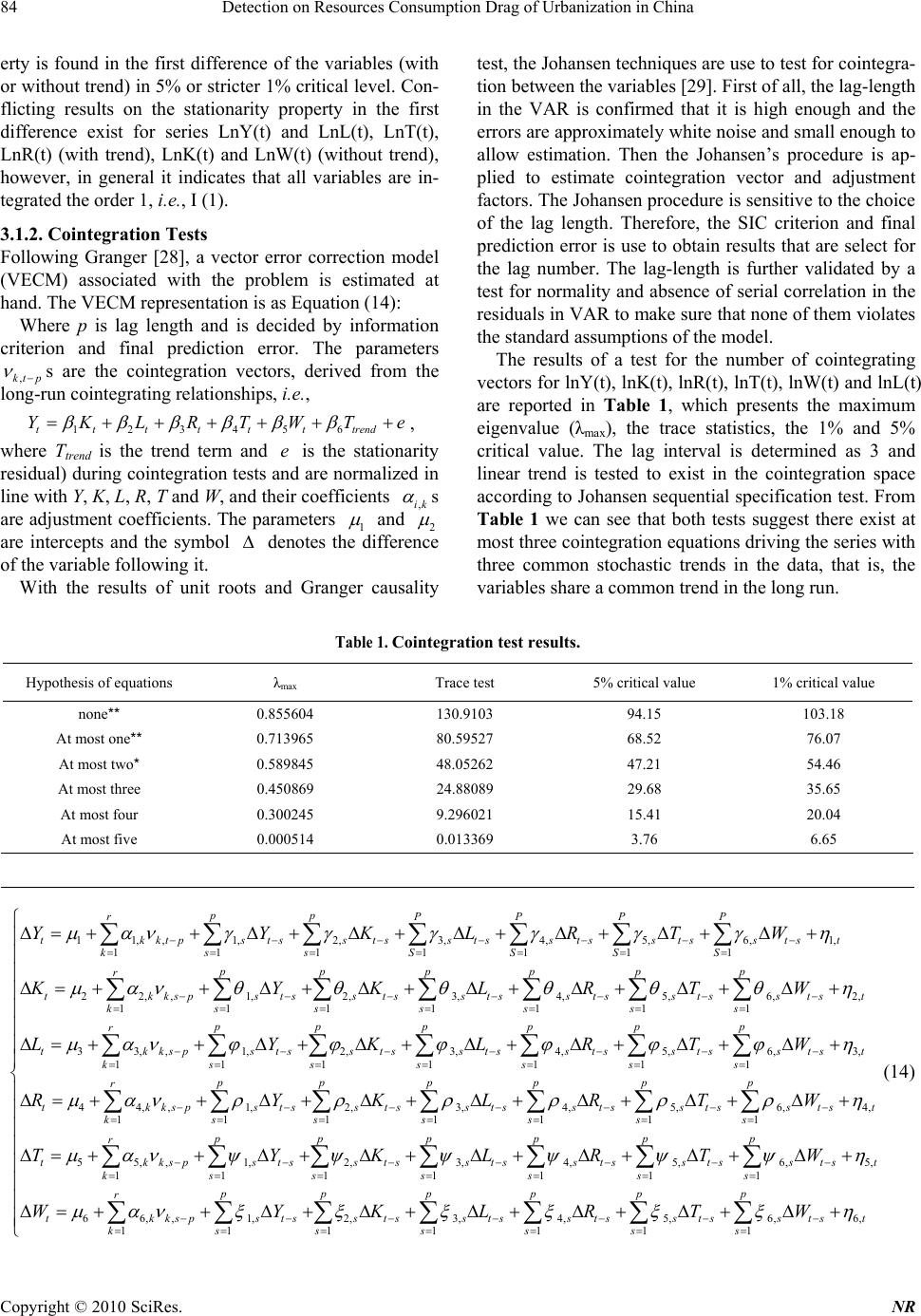 Detection on Resources Consumption Drag of Urbanization in China Copyright © 2010 SciRes. NR 84 erty is found in the first difference of the variables (with or without trend) in 5% or stricter 1% critical level. Con- flicting results on the stationarity property in the first difference exist for series LnY(t) and LnL(t), LnT(t), LnR(t) (with trend), LnK(t) and LnW(t) (without trend), however, in general it indicates that all variables are in- tegrated the order 1, i.e., I (1). 3.1.2. Cointegration Tests Following Granger [28], a vector error correction model (VECM) associated with the problem is estimated at hand. The VECM representation is as Equation (14): Where p is lag length and is decided by information criterion and final prediction error. The parameters ,kt p s are the cointegration vectors, derived from the long-run cointegrating relationships, i.e., 123456tttttttrend YKLRTWTe , where Ttrend is the trend term and e is the stationarity residual) during cointegration tests and are normalized in line with Y, K, L, R, T and W, and their coefficients ,ik s are adjustment coefficients. The parameters 1 and 2 are intercepts and the symbol denotes the difference of the variable following it. With the results of unit roots and Granger causality test, the Johansen techniques are use to test for cointegra- tion between the variables [29]. First of all, the lag-length in the VAR is confirmed that it is high enough and the errors are approximately white noise and small enough to allow estimation. Then the Johansen’s procedure is ap- plied to estimate cointegration vector and adjustment factors. The Johansen procedure is sensitive to the choice of the lag length. Therefore, the SIC criterion and final prediction error is use to obtain results that are select for the lag number. The lag-length is further validated by a test for normality and absence of serial correlation in the residuals in VAR to make sure that none of them violates the standard assumptions of the model. The results of a test for the number of cointegrating vectors for lnY(t), lnK(t), lnR(t), lnT(t), lnW(t) and lnL(t) are reported in Table 1, which presents the maximum eigenvalue (λmax), the trace statistics, the 1% and 5% critical value. The lag interval is determined as 3 and linear trend is tested to exist in the cointegration space according to Johansen sequential specification test. From Table 1 we can see that both tests suggest there exist at most three cointegration equations driving the series with three common stochastic trends in the data, that is, the variables share a common trend in the long run. Table 1. Cointegration test results. Hypothesis of equations λmax Trace test 5% critical value 1% critical value none** 0.855604 130.9103 94.15 103.18 At most one** 0.713965 80.59527 68.52 76.07 At most two* 0.589845 48.05262 47.21 54.46 At most three 0.450869 24.88089 29.68 35.65 At most four 0.300245 9.296021 15.41 20.04 At most five 0.000514 0.013369 3.76 6.65 11, ,1,2,3,4,5,6,1, 111 1111 22,, 1,2,3,4,5, 11 11 pp rPPPP tkktpstsstss tsstss tsstst kss SSSS ppp r tkkspstsstsstsstss ks sss YYKLRTW KYKLR 6, 2, 111 33, ,1,2,3,4,5,6,3, 111 11 11 44,, 1,2, 11 ppp tss tst s s pppppp r tkksps tsstss tsstss tsstst kssssss p r tkkspstssts ks TW LYKLRTW RYK 3,4,5,6, 4, 11111 55, ,1,2,3,4,5,6,5, 1111 11 1 66,, ppppp s tsstss tsstst sssss ppppp p r tk kspstsstsstsstsstsstst kss ssss tkks LRTW TYKLRTW W 1,2,3,4,5,6,6, 1111111 ppppp p r p s tsstss tsstss tsstst kssssss YKLRT W (14)  Detection on Resources Consumption Drag of Urbanization in China Copyright © 2010 SciRes. NR 85 3.2. Detected Results 3.2.1. Economic Growth Analysis The unit root test and cointegration tests show that series of lnY(t), lnK(t), lnR(t), lnT(t), lnW(t) and lnL(t) are non-stationarity, but there exist at most three cointegra- tion relationships among them. Therefore, a regression analysis can be implemented considering the potential multi-collinearity and autocorrelation among the vari- ables, and the weighted Least Squares (WLS) is use to eliminate the characters. With WLS regression and the model, the equation can be estimated as Equation (15): From Equation (15), we can calculate the elasticity of capital, energy, land and water. The value of , β, γ and θ is 0.3014, 0.2334, 0.0078 and 0.4211, respectively. With the data of China’s labor in 1978-2008, we can calculate the growth rate of labor n (n = 0.0252). 3.2.2. Urbanization Relation Estimation With per labor GDP as per capita output and percentage of urban population in total population as urbanization level, a regression analysis is made. Through D.W. and White Heteroskedasticity test, the statistic value F and R2 are 3.6179 (P = 0.0417) and 6.2850 (P = 0.043175). The datum suggests the existence of heteroskedasticity in the equation. To eliminate faults, the weights as wi = 1/e2 are taken to simulate the regression equation, and the equa- tion can be: ˆˆ 67.471712.5566 ln [0.0763] [0.0103] ( 888.5199)(1220.8420) uy (16) 20.9990,. .1.4387,1490456RDWF From Equation (16), the elasticity of urbanization to per capita output λ is calculate as 0.0794. 3.2.3. Resources Consumption Drags Analysis Noting that the drag land is only 0.0003 and it is much smaller than the data from Xue et al. [8] and Xie, et al. [9]. Xue et al. and Xie, et al. estimate the drags from land in China are 0.0132 and 0.0134 respectively. The differ- ences can partly attribute to the date used in the studies. Firstly, in the study of Xue et al. [8] and Xie et al. [9], the data of the available land area only includes datum of the arable area, forestry area and usable green area with- out the urbanized area. However, in practice it is too small to sustain the overall China’s economic growth. According to National Statistic Yearbook 2009 [21], the 68.6% of GDP derives from the urban area and the sig- nificance of it could not be neglected. Therefore, the ur- banized area is included in our study and the drag esti- mated from land inevitably inclines to reduce, which distinctly differs from the study of Xue et al. [8] and Xie et al. [9]. Secondly, the drag from energy consumption had not been calculated in Xue et al. [8] and Xie, et al. [9]. Energy shortage becomes the potential challenges to China’s economic growth, thus enhancing energy supply security and guaranteeing energy supply are of uttermost importance to China. China is short of oil resource and nearly half of domestic oil consumption imported cur- rently. In 2008, the aggregate energy import amounts to 285.79 billion tons standard coal equivalent (sce) and the percentage is still on an increase. It is estimated that in 2020 the number will rise as much as 60% if the current trend continues. Hence, if the influence of energy con- sumption is considered, the drag from land may decrease. In the study, the calculated drag from water is 0.0152, which is much higher than that of Xie et al. [9]. In the study of Xie et al. [9], the water data includes the amounts of rivers (0.96%) and the available water re- sources (i.e. the sum of surface water and groundwater subtracted by the surplus). Xie et al. [9] estimates the drag from water is only 0.0014 percent point. Obviously, the data of the available water resources is not equal to the total in China. In terms of the restriction of techno- logical progress, hydrological pollution and disequilibria distribution, the water supplying only amounts to 20.08% of the total water resource. However, we only use the total available water resources to estimate the drag. Therefore, the calculated drag from water must be smaller than that in the former research. In fact, China undergoes a water crisis resulting from more pollution, inferior management and faster economic growth. The statistic data by the State Statistics Bureau showed that 70% of water re- sources in lake and river are polluted. The water crisis occurs frequently in China, hence it is necessary for us to prevent water resources pollution with the rapid eco- nomic growth and urbanization [21]. t-1 ˆ ˆˆˆˆˆ Y=0.0513 + 0.3014k+ 0.2334R+ 0.0078T+ 0.4211W+ 0.0363L [0.0020][0.0236][0.0232] [0.0041] [0.0446][0.0046] (26.0827) (12.7830)(10.0588)(1.8987)(9.4457)(1.6458) (15) 20.9997,. .1.6406,53.8262RDWF  Detection on Resources Consumption Drag of Urbanization in China Copyright © 2010 SciRes. NR 86 With the calculated elasticity of urbanization to per capita output λ, resources consumption drag of China’s urbanization can be obtained. The drag from energy, land and water respectively are 0.1061, 0.0036 and 0.1914 and the aggregate drag is 0.3010. Clearly, the effects from energy, land and water resources during China’s urbanization process are significant. Because of the in- fluence of resources consumption on economic growth, the drag reduces annual growth rates of China’s urbani- zation by about 0.30 percent point. It can be seemed that the influence from water resources is the largest followed by energy consumption, and the smallest is land re- sources. If such drag is taken into account, how much will the annual growth rate of China’s urbanization reach in the next fifteen years? Whether urbanization can assist the implementation of the national strategy in the future? According to the Eleventh Five-Year Plan for Economic and Social Development, the top-level economic and social development creed in China [30], in 2015 the tar- get value of China’s urbanization is 50%, that is, annual growth rate of China’s urbanization will reach 0.7 per- cent point at that time. Unfortunately, if the current pro- duction mode keeps on the China’s urbanization level in 2015 will be only 47% because of the existence of growth drag. 4. Concluding Remarks Urbanization process has been accompanied by the in- creasing energy consumption, land as well as the avail- able water resources. Based on the neo-classical eco- nomic growth theory and the urbanization relation model, a resources consumption drag model of urbanization is developed and an empirical analysis based on China’s series data is made. The study shows that the drag from energy, land and water consumption under China’s ur- banization are respectively 0.1061, 0.0036 and 0.1914, and the aggregate drag is 0.3010. Obviously, energy, land and water resources play important roles in China's urbanization process. By comparison, the constraint of water is the largest and that of land resources is the smallest among them. Therefore, together with rapid ur- banization process in China, both the rational protection of water resources and the effective supply of energy resources should be highlighted by China’s government. Last but not least, due to resources restriction, if the balanced-growth-path with the more resource-dependent pattern is allowed to follow, in 2015 it is hard to achieve the strategic target of China’s urbanization. Clearly, the growth pattern more relying on the resources consump- tion cannot guarantee to achieve the strategic objectives. In terms of resource constraints, in particular, water re- sources and energy, if the pattern of resources unitization does not be adjusted, the drag will be significantly in- creasing with the rise of urban population and total pop- ulation in China. Therefore, the conventional pattern with excessive reliance on the resources has to be abandoned, in accordance with the high input and high concentration of economic production. It is worth notable that China’s urbanization should comply with the distribution of nat- ural resources, adhere to the planning and construction principle of compact cities and choose the development pattern of resource-economized cities. 5. Acknowledgements We gratefully acknowledge the helpful suggestions from the anonymous reviewers. This work was supported by National Natural Science Foundation of China (No. 40961009) and the Key Project of Chinese Ministry of Education (No: 210117). REFERENCES [1] R. M. Solow, “A Contribution to the Theory of Economic Growth,” Quarterly of Journal of Economics, Vol. 70, No. 1, 1956, pp. 65-94. [2] T. R. Malthus, “An Essay on the Principle of Population,” Oxford University Press, New York, 1797, pp. 21-42. [3] D. Romer, “Advanced Macroeconomics (Second Edi- tion),” The McGraw-Hill Companies Inc, New York, 1996, pp. 37-42. [4] A. Bruvoll, S. Glomsrod and H. Vennemo, “Enviromental Drag: Evidence from Norway,” Ecological Economic, Vol. 30, No. 2, 1999, pp. 235-249. [5] P. Dasgupta and G. Heal, “The Optimal Depletion of Exhaustible Resources,” The Review of Economic Studies, Vol. 41, 1974, pp. 3-28. [6] W. D. Nordhaus, “Lethal Model 2: The Limits to Growth Revisited,” Brookings Papers on Economic Activity, Vol. 2, 1992, pp. 1-58. [7] O. Tahvonen and J. Kuuluvainen, “Economic Growth, Pollution and Renewable Resources,” Journal of Envi- ronmental Economics and Management, Vol. 24, No. 2, 1993, pp. 101-118. [8] J. B. Xue, Z. Wang, J. W. Zhu and B. Wu, “An Analysis of Drag of China’s Economic Growth,” Journal of Fi- nance and Economics, Vol. 30, No. 9, 2004, pp. 5-14. [9] S. L. Xie, Z. Wang and J. B. Xie, “Drag of China,s Eco- nomic Growth on Water and Land,” Management World, No. 7, 2005, pp. 22-25. [10] B. L. II. Turner, W. C. Clark, R. W. Kates, J. F. Richards, J. T. Mathews and W. B. Meyer, “The Earth as Trans- formed by Human Action: Global and Regional Changes in the Biosphere over the Past 300 Years,” Cambridge University Press, Cambridge, 1990. [11] C. Weber and A. Puissant, “Urbanization Pressure and Modeling of Urban Growth: Example of the Tunis Met- ropolitan Area,” Remote Sensing of Environment, Vol. 86, No. 3, 2003, pp. 341-352. [12] L. Shen, S. H. Cheng, A. J. Gunson and H. Wan, “Ur-  Detection on Resources Consumption Drag of Urbanization in China Copyright © 2010 SciRes. NR 87 banization, Sustainability and the Utilization of Energy and Mineral Resources in China,” Cities, Vol. 22, No. 4, 2005, pp. 287-302. [13] C. Bao and C. L. Fang, “Water Resources Constraint Force on Urbanization in Water Deficient Regions: A Case Study of the Hexi Corridor, Arid Area of NW China,” Ecological Economics, Vol. 62, No. 3-4, 2007, pp. 508-517. [14] Z. H. Zhang, B. X. Chen, Z. K. Chen and X. Y. Xu, “Challenges and Opportunities for Development of China Water Resources in the 21st-Century,” Water Interna- tional, Vol. 17, No. 5, 1992, pp. 21-27. [15] J. K. Zhou, “Influence on Urban Water Cycle by Urbani- zation,” Southwest Water and Wastewater, Vol. 26, No. 6, 2004, pp. 4-7. [16] E. A. Z. Andrews and W. K. Donald, “Further Evidence on the Great Crash, the Oil-Price Shock and the Unit Root Hypothesis,” Journal of Business and Economic Statistics, Vol. 10, No. 3, 1992, pp. 251-270. [17] W. W. Ren, Y. Zhong, J. Meligrana, B. Anderson, W. E. Watt, J. K. Chen and H. L. Leung, “Urbanization, Land Use, and Water Quality in Shanghai 1947-1996,” Envi- ronment International, Vol. 29, No. 5, 2003, pp. 649-659. [18] H. Kondo, “Multiple Growth and Urbanization Patterns in an Endogenous Growth Model with Spatial Agglomera- tion,” Journal of Development Economics, Vol. 75, No. 1, 2004, pp. 167-199. [19] J. R. Harris and M. Todaro, “Migration, Unemployment and Development: A Two Sectors Analysis,” American Economic Review, Vol. 40, 1970, pp. 126-142. [20] J. S. Liang, “A Theoretical Analysis of Statistical Rela- tionship between Urbanization and Economic Develop- ment,” Journal of Natural Resources, Vol. 14, No. 4, 1999, pp. 351-354. [21] The National Statistics Bureau of China, “China Statisti- cal Yearbook 2009,” China Statistics Press, Beijing, 2009. [22] The National Statistics Bureau of China, “Statistical Issue of New China during Fifty Years,” China Statistics Press, Beijing, 1999. [23] State Environmental Protection Administration, “Key Po- Llutant Discharges Keep Rising,” 2006, pp. 1-4. http:// www.chinadaily.com.cn/china/2006-08/30/content_677238. html [24] Energy Information Agency, 2006, “Country Analysis Briefs: China,” 2008. http://www.eia.doc.gov/emeu/tabs/ china.html [25] G. S. Maddala and I. M. Kim, “Unit Roots, Cointegration, and Structural Change,” Cambridge University Press, Cambridge, 1998. [26] K. Hubrich, H. Lutkepohl and P. Saikkonen, “A Review of Systems Cointegration Tests,” Econometric Reviews, Vol. 20, No. 3, 2001, pp. 247-318. [27] S. Ng and P. Perron, “Lag Length Selection and the Con- struction of Unit Root Tests with Good Size and Power,” Econometrica, Vol. 69, No. 6, 2001, pp. 1519-1554. [28] C. W. J. Granger, “Causality, Cointegration, and Con- trol,” Journal of Economic Dynamic and Control, Vol. 12, No. 11, 1998, pp. 551-559. [29] S. Johansen, “Likelihood-Based Inference in Co-Inte- grated Vector Autoregressive Models,” Oxford University Press, Oxford, 1995. [30] The Central People’s Government of the People’s Repub- lic of China, “Eleventh Five-Year Plan for Economic and Social Development for 2006-2010,” The People Press, Beijing, 2006. |

