 Creative Education 2013. Vol.4, No.7, 430-439 Published Online July 2013 in SciRes (http://www.scirp.org/journal/ce) http://dx.doi.org/10.4236/ce.2013.47062 Copyright © 2013 SciRe s . 430 A Model for Assessing the Development of Students’ Creativity in the Context of Problem Posing Atara Shriki Oranim Academic College of E d u c a t i o n , Tivon, Isra e l Email: atarashriki@gmail.com Received April 19th, 2013; revised May 20th, 2013; accepted May 27th, 2013 Copyright © 2013 Atara Shriki. This is an open access article distributed under the Creative Commons Attribu- tion License, which permits unrestricted use, d i st ribution, and reproduction in any med ium, provid ed th e o riginal work is properly cited. In a changing technological society, creativity is recognized as the vehicle of economic and social growth. Although the education system has a central role in developing all students’ creativity, it is not often nur- tured in schools. Several conditions are offered to justify this situation, among them: external pressures to cover the curriculum and succeed in standardized tests that generally require rote implementation of rules and algorithmic thinking; teachers’ tendency to teach similarly to the way they themselves were taught as school students; relating creativity to giftedness, and therefore avoiding nurturing all students’ creativity; teachers’ difficulties in assessing their students’ creativity and its development due to a lack of an avail- able simple tool; and more. This paper is aimed at responding to the latter condition, suggesting a coher- ent and accessible tool or model for assessing students’ creativity and its development in the context of problem posing. The proposed model considers 4 measurable aspects of creativity-fluency, flexibility, originality and organization, and a total score of creativity that is based on relative weights of each aspect. Viewing creativity as relative, the scores for these 4 aspects reflect learner’s achievements in relation to his or her reference group. The proposed model has two flexible components—the first relates to teach- ers’ interpretation of originality, and the second relates to the weights they may wish to ascribe each as- pect of creativity. In addition, it is suggested to provide learners with a graphical display of their scores and progress in order to enable them to refine their products in successive iterations. The examples in this paper are taken from mathematics; however the proposed model can be adapted to any other discipline. Keywords: Evaluation of Creativity; Problem Posing; The “What-If-Not?” Strategy; Self-Assessment of Creativity Introduction Creativity is generally perceived to be a key driver of social and economic changes. One would, therefore, anticipate that the education system would strive to nurture students’ creativity (Beghetto, 2006). However, although teachers believe that ma- thematical creativity can and should be nurtured in school in most schools it is normally not encouraged (Sriraman, 2005). As a result most students are provided with few opportunities to experience creative learning and thinking (Silver, 1997). This reality is a result of a combination of several circum- stances, among them: (i) Teachers are subjected to various ex- ternal pressures, such as covering the written curriculum, and help their students to succeed on both teacher generated and standardized tests (Beghetto, 2006). The education system em- phasizes the importance of achieving high test scores, and too often teachers are judged based solely on their students’ success on these tests. For the most part, standardized tests generally require rote implementation of rules and algorithmic thinking. Furthermore, standardized tests are not designed to formally assessing mathematical creativity (Chamberlin & Moon, 2005). As a result, teachers tend to focus on memorization and algo- rithms, rather than on nurturing students’ creativity; (ii) Teach- ers are inclined to teach similarly to the way they themselves were taught at school (Hall, Fisher, Musanti, & Halquist, 2006). As school students, most of them experienced mathematics education that did not place an emphasis on developing creativ- ity. With insufficient role models in their formative years of schooling to draw upon as positive examples, it is reasonable to assume that, as teachers, they may not have naturally acquired sufficient tools and methods aimed at nurturing students’ crea- tivity. Further exacerbating the problem is a shortage of appro- priate learning materials, which makes it difficult for teachers to sustain learning environments that nurture creativity (Silver, 1997); (iii) Specifically to mathematics, there is a problem that stem from teachers’ beliefs that creative thinking is not ex- pressed across the curriculum, but is restricted to liberal arts and humanities. In their minds, examples of creative outcomes refer mainly to drawing, painting, writing and acting (Andiliou & Murphy, 2010), viewing mathematics as offering fewer op- portunities for creativity; (iv) Many teachers relate creativity to giftedness, and therefore avoid nurturing all students’ creativity (Aljughaiman & Reynolds, 2005; Sriraman, 2005); (v) Teach- ers face difficulties in assessing their students’ creativity and its development due a lack of an available simple tool and there- fore unable to implement a systematic approach to develop stu- dents’ creativity (Shriki, 2010). This paper is based on two main premises: (i) Nurturing stu-  A. SHRIKI dents’ creativity is not only possible at all ages and ability lev- els, but that it should be an integral part of the regular discipli- nary curriculum; (ii) Providing teachers with a practical tool for nurturing students’ creativity and assessing their progress might inspire them to integrate appropriate activities in their regular teaching. Given this stance, I plan to offer a model for assessing the development of students’ creativity in the context of inquiry assignments that have a component of problem posing. The problem posing approach encourages students to ask questions, explore a range of answers, and develop a critical perspective. It is also considered to be strongly associated with fostering creativity. The model being suggested uses four measurable aspects of creativity: fluency, flexibility, originality, and gener- alization. In addition, I intend to show that teachers’ and stu- dents’ self-assessment of their own progress in each of these aspects contributes to their development of creativity in the context of problem posing. All the examples in this paper are taken from mathematics, as well as some specific references to mathematics education; however, the proposed model can be adapted to every other discipline. A Brief Literature Background Interest in fostering creativity in modern education first sur- faced in the 1950’s (Craft, 2001). The topic has garnered sig- nificant worldwide attention since the late 90’s, leading some to suggest that creativity has gained acceptance as a catalyst for social and economic change (Lin, 2011). In as much as creativ- ity is considered essential for future success in life (NACCCE, 1999), it is incumbent upon teachers to create stimulating learning environments that are likely to nurture students’ crea- tivity. Indeed, research has acknowledged the fundamental role of education in nurturing students’ creativity as part of its wider responsibility to instill content knowledge (Lin, 2011). As a result, educators have shown interest in exploring and enhanc- ing creativity (Henry, 2009); assume that creativity can be de- veloped through explicit instruction (Fryer, 1996); and that all students possess an innate sense of creative, given that they have a natural curiosity for trying out new things (Feldman & Benjamin, 2006). Turning specifically to mathematics, it is be- lieved that genuine mathematical activities are closely related to creativity (Silver, 1997), and developing students’ mathematics creativity ought to be one of the primary goals of mathematics education (NCTM, 2000). In this section I present a brief literature survey that relates to some common definitions of creativity and its relation to posing mathematical problems. I will then introduce the “What If Not?” (WIN) strategy as a means for posing new mathematical problems based on a given problem. Finally, I will relate to students’ gains from engaging in self-assessment of their own products. Creativity Creativity “seems to be one of those words that although commonly used is not easy to define. We may use the term re- gularly, but can struggl e if asked to put into words sp ecifically to what we are referring” (Henry, 2009: p. 200). Educational and psychological researchers have explored the nature of creativity for more than a century (Plucke r, Beghe t t o, & Dow, 2004). This has resulted in a wealth of research aimed at understanding, explaining, and assessing the development of creativity over the years (Andiliou & Murphy, 2010) and examining its source and expression in human experience (Silver, 1997). Furthermore, there are over one hundred contemporary definitions of creativ- ity (Mann, 2006). Most of these definitions are vague or inade- quate due to the multifaceted nature of creativity (Sriraman, 2005) and none are universally accepted (Treffinger, Young, Selby, & Shepardson, 2002). Adding to this complexity, Henry’s (2009) literature review indicates that creativity has been re- searched through the lens of, at least, four different perspectives: the creative process, the creative person, the creative environ- ment, and the creative product. Drawing on Torrance’s (1974) definition of creativity, in the context of this paper I refer to four of its aspects: fluency, flexi- bility, novelty (or or i gi nality), and organization. “Fluency refers to the number of ideas generated in response to a prompt; fle- xibility to apparent shifts in approaches taken when generating responses to a prompt; and novelty to t he o rigina lity o f th e id eas generated in response to a prompt” (Silver, 1997: p. 97). Orga- nization refers to the number of generalizations (Brandau & Dossey, 1979). Of the four aspects listed in Torr ance’s definition of creativity, novelty or originality is widely acknowledged as the most a ppropria te asp ect becau se cre ativit y is genera lly view- ed as a process related to the generation of original ideas, ap- proaches, or actions (Leikin, 2009; Shriki, 2010). Problem Posi n g a nd Nurtu r i n g S tu dents’ Creativity In order to suppo rt the development of students’ mathematical creativity, mathematics educators should view creativity as “an orientation or disposition toward mathematica l activit y t h a t can be fostered broadly in the general school population.” For that matter, teachers should implement “inquiry-oriented mathema- tics instruction which includes problem-solving and problem- posing tasks” (Silver, 1997: p. 75). Refraining from developing students’ mathematical creativity might lead them to perceive mathematics as a set of skills and rules to memorize and cause them to lose their natural curiosity and interest in mathematics (Mann, 2006). While contemporary views of creativity differ with respect to the nature of the trait and to the ability of individuals to produce creative outcomes, there is a growing consensus regarding the centrality of problem posing and problem solving processes within the creative act (Silver, 1997). According to Silver, pro- blem posing has long been viewed “as a characteristic of crea- tive activity or exceptional talen t in many fields of human endea- vor” (p. 76). Supporting his argument, Silver maintains that al- though mathematicians may solve problems that have been pos- ed by others, they generally formulate their own problems based on personal experiences and interests. Indeed, Albert Einstein believed that “The formulation of a problem is often more es- sential than its solution, which may be merely a matter of ma- thematical or experimental skills. To raise new questions, new possibilities, to regard old questions from a new angle, requires creative imagination and marks real advance in science” (Ein- stien & Infeld, 1938, in Ellerton & Clarkson, 1996: p. 518). However, this perception stands in stark contrast to school- based math ematics where, in most c ases, problems are pr esented by teachers and in textbooks. Therefore, in order to develop students’ mathematical creativity, teacher should engage their students in activities that include problem posing and provide them with developmentally appropriate, high interest opportu- nities to pose their own problems and suggest solutions (Mann, Copyright © 2013 SciRe s . 431  A. SHRIKI 2006). As students pose their own problems, they become in- novative, cr e ativ e, acti ve learners. They improve their reasoning, develop diverse and flexible thinking, and enrich and strengthen their knowledge and problem solving skills. Some have sug- gested that they might even change their perception of mathe- matics (Brown & Walter, 1990), as well as increase their ability with respect to the central aspects of creativity: fluency, flexi- bility, originality and organization (Silver, 1997). Problem posing involves generating new problems and ques- tions aimed at exploring a given situation, as well as the refor- mulation of a problem over the course of its solution (Silver, 1994). This can be done by varying and reversing the “knowns” or givens, or by varying the constraints of the problem (Marti- nez-Cruz & Contreras, 2002). When faced with new and novel mathematical situations, students are required to validate their thinking and selection of mathematical co ncepts use d to generate their answers, thus leading them to develop and deepen their mathematical knowledge. When students formulate new prob- lems, they develop a sense of ow nership over the subject matter, which results in an increase of curiosity in and enthusiasm for learning mathematics (Cunningham, 2004). Employing the “What-If-Not?” Strategy for Posing Problems In order to enable studen ts to gen erate math emati cal proble ms, Silver (1997) suggests employing the instructional approach de- veloped by Brown and Walter (1969, 1990), often termed as the “What-If-Not?” strategy. This method of instruction requires students to generate new problems based on previously solved problem, through a process of varying the conditions or goals of the original problem (Silver, 1997). By implementing this ap- proach, teachers are likely to support the development of stu- dents’ creativity in mathematics. The “What-If-Not?” (WIN) strategy suggested by Brown and Walter (1969, 1990) is based on the idea that modifying the components of a given problem can yield new and stimulating problems that ultimately may result in some interesting inves- tigations and may lead to the uncovering of mathematic regu- larities. This approach to problem posing leads the students through three levels of inqu iry, starting with a re- examination of a given problem, in order to discover new related problems. In the first phase, students are asked to produce a list of the prob- lem’s attributes or conditions. In the second phase, students focus on each attr ibute in the l ist, address the WIN que stion, and suggest alternatives to the attributes. The third phase consists of posing new problems and questions based on the alternatives that arose during the second phase. Going through these phases students may develop new perspectives: “Only after we have looked at so meth ing, not as it ‘is’ but as it is turned inside out or upside down, do we see its essence or significance” (Brown & Walter, 1990: p.15). Implementing the WIN strategy enables teachers to expand their teaching repertoire, thereby generating learning environments that encourage discussion of various ideas and demonstrate to students that there is often more than one “right way” to solve a given problem. This approach also enables students to consider the meaning of a problem, rather than simply focusing on finding its solution. According to Haylock (1986), mathematical assignments should include problem posing, problem solving, and redefini- tion. The WIN strategy approach includes all three of these components. The first level, in which students list the attributes of a given problem, provides the opportunity to rethink mathe- matical objects and concepts. The second level, addressing the WIN question and suggesting alternatives, necessitates redefi- nition of mathematical situations. For that matter students have to consider the “ logical contexts and conditions that underlie the determination of how to select certain givens and group them together in order to create a coherent mathematical situation” (Lavy & Shriki, 2010: p. 19). The third level, posing new prob- lems and questions and subsequently solving at least one of them, are closely connected to creativity (Silver, 1997). Evaluati o n o f Crea t i vi ty The activities of problem posing and the creative aspects of such activitie s—fluency, flexib ility, novelty, and organization— are well established within the practice of assessing creativity. Both processes and products of activities that involve problem posing can be evalua ted in order to determine t he extent to which creativit y is pr es ent. For that mat ter, it is poss ible to exam ine the novelty of the problem formulation or the problem solution, the extent to which modifications were evident, and the number of formulations or reformulations produced or the number of dif- ferent solu tion pat hs invest igated . Classi fying c reativi ty in te rms of fluency, flexibility, novelty and organization also provides teachers with an eas y sch ema for evalu ating th e tra it (Brand au & Dossey, 1979; Silver, 1997). Self-Assessment of Creativi ty The Standards of the NCTM (2000) recommend engaging students in self-assessment in order to nurture their confidence and independenc e in lear ning mat hematic s. Skill s a cqui red t houg h self-assessment are actually life skills that are applicable to a wide range of situations (Smith, 1997). Engaging students in self-assessment of attaining goals they set to themselves “al- lows students ownership over and responsibility for their learn- ing as well as providing real choices about what they learn. It provides students with opportunities to spend time reflecting on their learning… through being engaged in self-assessment, stu- dents become deeply self-motivated and independent learners.” (p. 7). Moreover, students’ involvement in assessing their own progress in learning adds reflection and metacognition to their learning. Students enjoy participating in self-assessment and observing their progress using graphical displays, and are able to use it for articulating the value of their own study (Brookhart, Andolina, Meganzuza, & Furman, 2004). Relating specifically to self-assessment of one’s own creativity, Chamberlin & Moon (2005) believe that such process in itself requires creativity and will, in return, enable students to refine their products in suc- cessive iterations. Therefore, it is recommended to enable stu- dents to assess their own creativity and its development. How- ever, in order to help students assess their performance and pro- gress, they should be provided with clear and easily understood guidelines (Enz & Serafini, 1995), and they need to be taught how to self-assess themselves and get a proper support from their teachers (Brookhart et al., 2004). Research indicates (e.g. Enz & Serafini, 1995) that after gaining a suitable training, stu- dents are able to keep the self-assessment with little or no as- sistance from their teacher, and students who are trained in self- assessment outperform their peers who do not receive such pre- paration. Copyright © 2013 SciRe s . 432  A. SHRIKI A Model for Evaluating Creativity and Its Development in the Context of Problem Posing Considering th e mult ifaceted nature of creati vity, it is obvious that selecting a definition that embraces all mathematical areas or types of mathematical assignments would be impossible. In this current framework, the proposed model is intended to eva- luate creativity and its development in the context of inquiry tasks that have a component of problem posing through relating to fluency, flexibility, originality, and organization. Drawing on Balka (1974), Brandau & Dossey (1979), and Torrance (1974), fluency is measured by the number of different problems posed, flexibility is measured by the number of different categories of the posed problems, originality is measured by the relative in- frequency of the problems, and organization is measured by the number of problems stated as generalizations. As pointed out by Brandau & Dossey, all of these variables are highly significant and positively correlated. The view of personal creativity, as a quality that can be de- veloped in school students, requires a distinction between rela- tive and absolute creativity (Leikin, 2009; Sriraman, 2005). While absolute creativity is associated with remarkable histori- cal works of pro minent mathem aticians, r elative c reativity refers to discoveries made by a specific person within a specific ref- erence group. This distinction is expressed in Leikin’s (2009) model aimed at evaluating mathematical creativity in the con- text of multiple solutions to a given problem. Leikin (2009) suggested the notion of “solution spaces”. She referred to “Ex- pert solution spaces” as those “that include the most complete set of solutions to a problem known at a particul ar time”, where in school mathematics “expert solution spaces include conven- tional solution spaces, which are those generally recommended by the curriculum, displayed in textbooks, and usually taught by the teachers. By contrast, unconventional solution spaces in- clude solutions based on strategies usually not prescribed by the school curriculum, or that the curriculum recommends with respect to a different type of problem”. “Individual solution spaces” are perceived as “collections of solutions produced by an individual to a particular problem”; and “Collective solu- tion spaces” refer to the collection of all “individual solution spaces within a particular community” (Leikin, 2009: p. 133). Drawing on this distinction and adapting it to the context of problem posing, in the proposed model below each student receives a total as well as relative score of fluency, flexibility, originality and organization. The individual total score is equi- valent to the meaning of “individual space”, and the individual relative score refers to the frequency of a posed problem in- cluded in the individual space in relation to its frequency in the collective space, as will be explained below. Guidelines for Scoring the Four Aspe cts of Creativity The scoring process refers to the third level of the WIN strategy, wher e learners have to relate to the list of at tributes they produced (first level) and their possible alternatives (second le- vel) to pose new problems. In order to determine s tudents’ score for each aspect of creativity, and an overall creativity score, the following steps are applied: a. Fluency scor ing Student’s total score of fluency is determined by totaling the number of different new problems he or she posed, based on a given problem. The relative score of fluen cy is det ermined in t he following manner: the student in the reference group who re- ceived the highest total score of fluency is given a score of 100 for relative fluency. All other students’ r elative scores of fluency are determined according to the highest score. For example, if the highest total score is 20 (namely, each student posed 20 different problems at the most), then those who posed 20 prob- lems receive a relative score of 100. Those who posed, for in- stance, 12 problems receive a relative score of 60. b. Flexibility scoring Student’s total score for flexibility is determined by the total number of different categories that are constituted by the posed problems. The relative score of flexibility is determined simi- larly to the relative score calculation used for fluency. c. Originality scoring Since originality is, by its very nature, relative there is a need to predetermine the condition for originality. If we take, for example, all the problems posed by a third of the students to be the “upper” limit for originality, then all students who posed pro- blems that 33% or less of th e students posed will receive a score for originality. Obviously, this “upper limit” can vary from one class to another. Other stu dents wi l l receive a score of 0. The re- lative s core of or iginalit y is d eter mined in the fol lowing manner: Assume that the group consists of 30 students. In this case only problems that were posed b y 10 or fewer students ar e considered for scoring originality. The students who posed the largest num- ber of such problems receive a score of 100 for originality. Other students who posed problems th at are consider ed for scoring ori- ginality r eceive a relat ive score sim ilarly to the calcul ations used for scoring fluency and flexibility. d. Organization (or generalization) scoring Students’ tot al score for or ganizatio n is determin ed accordi n g to the number of posed problems that are formulated as a gen- eralization , and then the r elative s core is calcula ted simila r to the above cases. e. An overall total score of creativity Finally, the overall score of creativity is determined, assigning a weight for each of the four relative scores. Determining rela- tive weighting is subjected to the teachers’ discretion, according to the importa nce th ey ascribe to each as pect. Cle arly, the b eliefs teachers hold about creativity is likely to influence how they define, operationalize, and evaluate students’ creativity (Andi- liou & Murphy, 2010). Therefore, it is important to provide teachers with the freedom to determine each component’s weight, adaptin g it to their p refer ences, em phasiz es and te aching goals. Demonstr ating the S c or i ng Process In this section I demonstrate the scoring process, illustrating how to set the total and relative scoring for fluency, flexibility, and organizati on; the scoring for origin ality; and the final overall scoring for creativity. This demonstration is based on results taken from a study carried out by Lavy & Shriki (2010). In this study, 25 prospective teachers were engaged in problem posing in geometry through implementing the WIN strategy. The given problem was taken from Hönsberger (1985: p. 81): Triangle ABC is inscribed in circle O. D is a variable point on the cir- cumference of O. Perpendiculars are drawn from D to AB and AC. E and F are intersection points of the perpendiculars with the side of the tri angle, res pectivel y. Determi ne the po sition of D whereby EF is of maximal length. Based on this problem, the prospective teachers posed 46 different problems that were classified into 12 different categories. Each problem was as- Copyright © 2013 SciRe s . 433 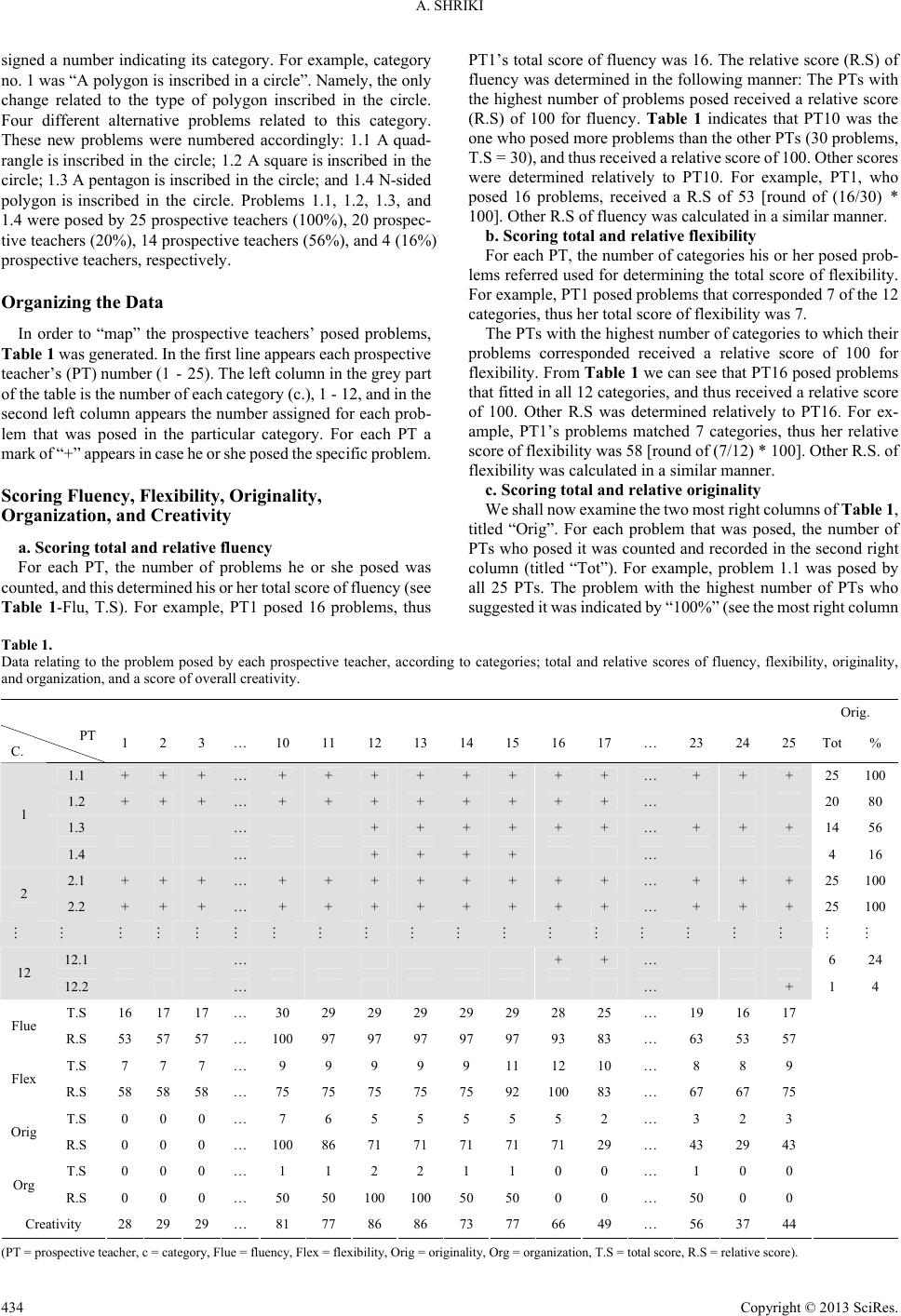 A. SHRIKI Copyright © 2013 SciRe s . 434 PT1’s total score of fluency was 16. The relative score (R.S) of fluency was determined in the following manner: The PTs with the highest number of problems posed received a relative score (R.S) of 100 for fluency. Table 1 indicates that PT10 was the one who posed more problems than the other PTs (30 problems, T.S = 30), and thus received a relative s core of 10 0. Other scor es were determined relatively to PT10. For example, PT1, who posed 16 problems, received a R.S of 53 [round of (16/30) * 100]. Other R.S of fluency was calculated in a similar manner. signed a number indicating its category. For example, category no. 1 was “A polygon is inscribed in a circle”. Namely, the only change related to the type of polygon inscribed in the circle. Four different alternative problems related to this category. These new problems were numbered accordingly: 1.1 A quad- rangle is inscribed in the circle; 1.2 A square is inscribed in the circle; 1.3 A pentagon is inscribed in the circle; and 1.4 N-sided polygon is inscribed in the circle. Problems 1.1, 1.2, 1.3, and 1.4 were posed by 25 prospective teachers (100%), 20 prospec- tive teachers (20%), 14 prospective teachers (56%), and 4 (16%) prospective teachers, respectively. b. Scoring total and relative flexibility For each PT, the number of categories his or her posed prob- lems referred used for determining the total score of flexibility. For example, PT1 posed problems that corresponded 7 of the 12 categories, thus her total score of flexibility was 7. Organizing the Data The PTs with the highest number of categories to which their problems corresponded received a relative score of 100 for flexibility. From Table 1 we can see that PT16 posed problems that fitted in all 12 categories, and thus received a relative score of 100. Other R.S was determined relatively to PT16. For ex- ample, PT1’s problems matched 7 categories, thus her relative score of flexibility was 58 [round of (7/12) * 100]. Other R.S. of flexibility w as calculated in a similar manner . In order to “map” the prospective teachers’ posed problems, Table 1 was g enerated. In the first line app ears each prospective teacher’s (PT) number (1 - 25). The left column in the grey part of the table is the number of each categor y (c.), 1 - 12, and in the second left column appears the number assigned for each prob- lem that was posed in the particular category. For each PT a mark of “ +” appears in case he or she posed the specif ic problem. c. Scoring total and relative originality Scoring Fluency, Flexibility, Originality, Organization, and Creativ ity We shall n ow exami ne the two most right columns of Table 1, titled “Orig”. For each problem that was posed, the number of PTs who posed it was counted and recorded in the second right column (titled “Tot”). For example, problem 1.1 was posed by all 25 PTs. The problem with the highest number of PTs who suggested it was indicated by “100%” (se e the most right column a. Scoring total and relative fluency For each PT, the number of problems he or she posed was counted, and this determined his or her total score of fluenc y (see Table 1-Flu, T.S). For example, PT1 posed 16 problems, thus Table 1. Data relating to the problem posed by each prospective teacher, according to categories; total and relative scores of fluency, flexibility, originality, and organization, an d a score of overall creativity. Orig. PT C. 1 2 3 … 10 11 12 13 14 15 16 17 … 23 24 25 Tot% 1.1 + + + … + + + + + + + + … + + + 25100 1.2 + + + … + + + + + + + + … 2080 1.3 … + + + + + + … + + + 14 56 1 1.4 … + + + + … 4 16 2.1 + + + … + + + + + + + + … + + + 25100 2 2.2 + + + … + + + + + + + + … + + + 25100 12.1 … + + … 6 24 12 12.2 … … + 1 4 T.S 16 17 17 … 30 29 29 29 29 29 28 25 … 19 16 17 Flue R.S 53 57 57 … 100 97 97 97 97 97 93 83 … 63 53 57 T.S 7 7 7 … 9 9 9 9 9 11 12 10 … 8 8 9 Flex R.S 58 58 58 … 75 75 75 75 75 92 100 83 … 67 67 75 T.S 0 0 0 … 7 6 5 5 5 5 5 2 … 3 2 3 Orig R.S 0 0 0 … 100 86 71 71 71 71 71 29 … 43 29 43 T.S 0 0 0 … 1 1 2 2 1 1 0 0 … 1 0 0 Org R.S 0 0 0 … 50 50 100100 50 50 0 0 … 50 0 0 Creativity 28 29 29 … 81 77 86 86 73 77 66 49 … 56 37 44 (PT = prosp ective teacher, c = category, Flue = fluency, Flex = flexibility , Orig = originality, Org = organization, T.S = total score, R.S = relative score). 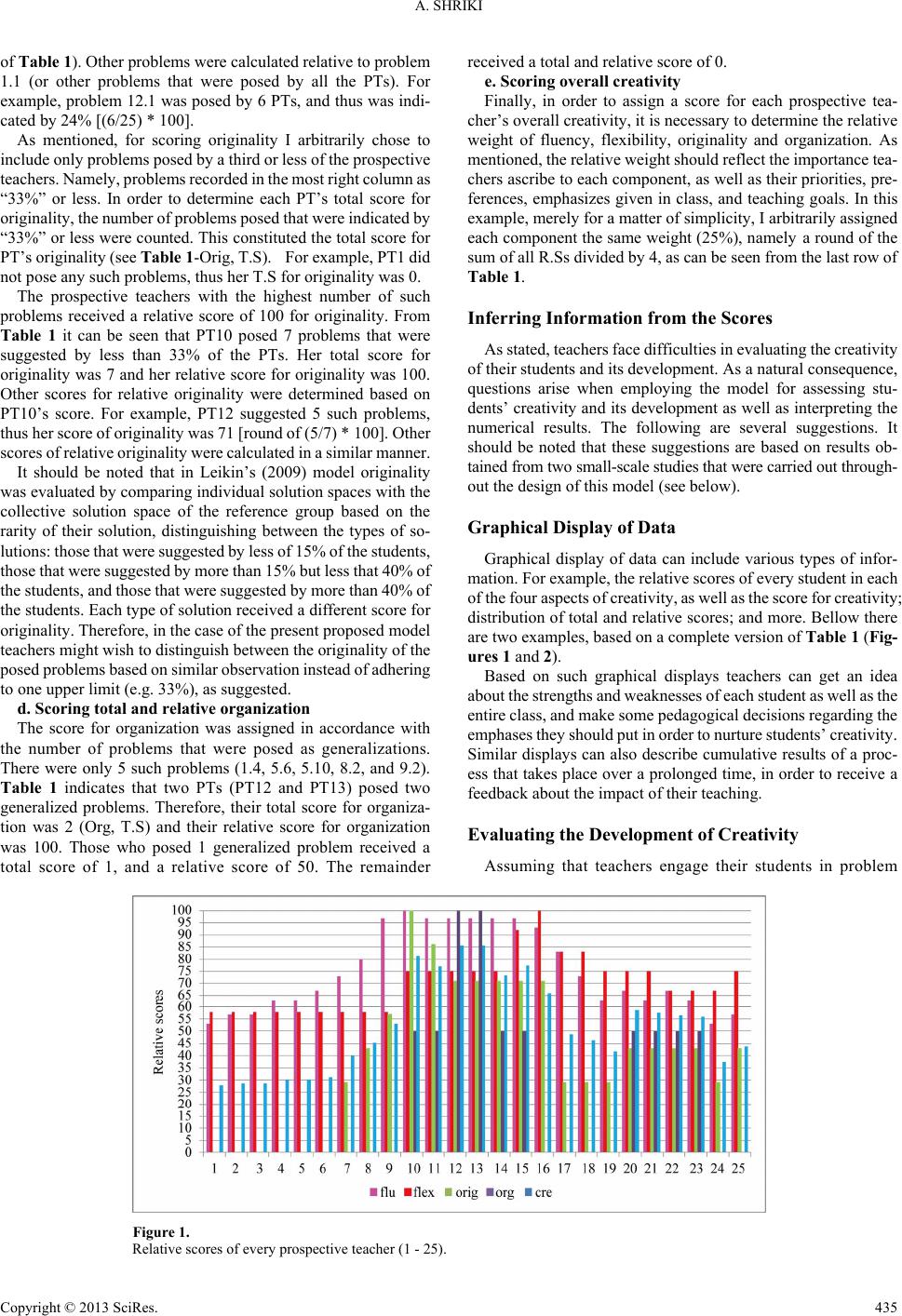 A. SHRIKI of Table 1) . Oth er problems wer e calculated relative to problem 1.1 (or other problems that were posed by all the PTs). For example, problem 12.1 was posed by 6 PTs, and thus was indi- cated by 24% [(6/25) * 100]. As mentioned, for scoring originality I arbitrarily chose to include only problems posed b y a third or less of the prospectiv e teachers. N amely, problem s recorded in the most right column as “33%” or less. In order to determine each PT’s total score for originality, the number of problems posed tha t were indi cated b y “33%” or less were counted. This constituted the total score for PT’s originalit y (se e Table 1-Orig, T.S). For example, PT1 did not pose any such problems, thus her T.S for originality was 0. The prospective teachers with the highest number of such problems received a relative score of 100 for originality. From Table 1 it can be seen that PT10 posed 7 problems that were suggested by less than 33% of the PTs. Her total score for originality was 7 and her relative score for originality was 100. Other scores for relative originality were determined based on PT10’s score. For example, PT12 suggested 5 such problems, thus her score of originality was 7 1 [round of (5/7) * 100]. Other scores of r elative orig inality were calculated in a similar m anner. It should be noted that in Leikin’s (2009) model originality was evaluated by comparing individual solution spaces with the collective solution space of the reference group based on the rarity of their solution, distinguishing between the types of so- lutions: those that were suggested by less of 15% of the students, those that were suggested b y more than 15% but less that 40 % of the students, and those that were suggested b y more than 40% of the students. Each type of solution received a different score for originality. Therefore, in the case of the present proposed model teachers might wish to distinguish between the originality of the posed problems based on similar observation instead of adhering to one upper limit (e.g. 33%), as suggested. d. Scoring total and relative organization The score for organization was assigned in accordance with the number of problems that were posed as generalizations. There were only 5 such problems (1.4, 5.6, 5.10, 8.2, and 9.2). Table 1 indicates that two PTs (PT12 and PT13) posed two generalized problems. Therefore, their total score for organiza- tion was 2 (Org, T.S) and their relative score for organization was 100. Those who posed 1 generalized problem received a total score of 1, and a relative score of 50. The remainder received a total and relative score of 0. e. Scoring overall creativity Finally, in order to assign a score for each prospective tea- cher’s overall creativity, it is necessary to determine the relative weight of fluency, flexibility, originality and organization. As mentioned, the rela tive we ight shou ld reflect the im portance tea- chers ascribe to each component, as well as their priorities, pre- ferences, emphasizes given in class, and teaching goals. In this example, merely for a matter of simplicity, I arbitrarily assigned each component the same weight (25%), namely a round of the sum of all R.Ss divided by 4, as can be seen from the last row of Table 1. Inferring Information from the Scores As stated, tea chers face d ifficulti es in evalu ating the c reativity of their students and its development. As a natural consequence, questions arise when employing the model for assessing stu- dents’ creativity and its development as well as interpreting the numerical results. The following are several suggestions. It should be noted that these suggestions are based on results ob- tained from two small-scale studies that were carried out through- out the design of this model (see below). Graphical Display of Data Graphical display of data can include various types of infor- mation. For exam pl e, t he r elat iv e s cor es o f ever y s tudent in each of the four aspe cts of creat ivity, as well as the score for cre ativity; distribution of total and relative scores; and more. Bellow there are two examples, based on a complete version of Table 1 (Fig- ures 1 and 2). Based on such graphical displays teachers can get an idea about the strengths and weakness es of each student as well as the entire class, and make some pedagogica l decisions regardi ng the emphases they should put in order to nurture students’ creativity. Similar displays can also describe cumulative results of a proc- ess that takes place over a prolonged time, in order to receive a feedback about the impact of their teaching. Evaluating t he Develop me nt of Creat ivity Assuming that teachers engage their students in problem Figure 1. Relative scores of every prospective teacher (1 - 25). Copyright © 2013 SciRe s . 435  A. SHRIKI Figure 2. Distribution of relative scores. posing assignments for an extended period of time, how can teacher employ the proposed model for assessing the develop- ment of their students’ creativity in order to make educational decisions? What indicators might serve this purpose? The model allows producing the following four numerical values: to tal scor e s, relative scores , averages, and s ta nd ar d devi- ations. The strengths and weaknesses of these numerical values for making educational decisions are as follows: a. Total scores The total scores for fluency, flexibility, originality and orga- nization cannot be used for assessing the development of crea- tivity b ecause th e num ber of p rob lems that can b e posed throug h employing the WIN strategy, and the resulted categories, might depend on the richness of attributes that are embedded in the original problem. However, total scores might be used in cases where teachers wish to make comparisons between classes that work on the same problems. Such a comparison is valuable mainly when teachers wish to examine the impact of different approaches intended to engage their students in problem posing assignments, or compare between students learning at different levels of mathematics or different age groups with respect to the impact of engaging them in posing problems. b. Average relative scores In the case of relative scores, a significant increase in the av- erage of any of the relative scores indicates that some students developed their creativity much more than others. In such cases, special attention might be given to students whose relative scores did not change much with time. Alternatively, it may indicate that creativity is indeed innate, and students that are more creative than oth er from the outset show a gr eater tendency to keep develop their creativity. Minor or no changes might im- ply that the entire class, as a reference group, either did not progress or all students exhibited similar progress (or regres- sion). c. Standard deviations Assuming that practicing the WIN strategy over and over again will not cause a decrease in mathematical creativity, a decrease of st andard deviat ion in any of th e measures implies the development of creativity of the class as a whole. Obviously, this is the most desirable situa tion. Therefore, an increase or decrease in standard deviations should serve as a primary indicator for examining the development, lack of development, or perhaps a decrease of creativity attributed to the class as a group of refer- ence. If indeed, creativity of all students can be developed through appropriate education, as suggested by the above men- tioned research literature, then we would expect a gradual re- duction in standard deviations over time. However, a gradual increase in standard deviation might support theories that main- tain that creativi ty is inna te, and that onl y except ional peopl e can demonstrate c reative b ehavior. It s hould be noted that in order to be able to tra ck c hanges, there is a need to predetermine the “up- per limit” used for scoring originality, as well as the weight of each component of creativity, and adhere it. Otherwise, tracing changes over time would be impossible. Some Insights Gained from Using the Model in Practice As mentioned, the proposed model was designed through carrying our two small-scale studies. In the first study 6 upper- elementary mathematics teachers were engaged in a series of 5 problem posing activities employing the WIN strategy. All the initial problems were taken from common school textbooks in order to demonstrate the idea that problem posing can easily become an integral par t of school curr iculum. B y t he end of e ach activity th e teachers presented their posed problems and tog ether categorized the problems in order to gain an unders tanding about the meaning of c ategor ization . In additi on, the te achers anal yzed the appropriateness of each posed problems (see below). Then I generated a table similar to Table 1, and each teacher received, personally, only the information that was relevant to his or her total and re lative scor es in a form at of graph ical displa y. Starting from the second activity the graphical display included cumula- tive scores (see example in Figure 3). This graphical display was intended to help the teachers trace their progress/withdra- wal compared to his or her reference group. During the entire process the teachers documented their work in a reflective jour- nal, and referred to aspects that concerned their perspective of themselves as learners of mathematics, their mathematical crea- tivity, the pedagogical insights they had gained, and the role played by their ability to self-assess their progress/withdrawal. In the second study eac h teacher r epeated the process wit h one of his or her classes. The results of these studies allowed formulating the proposed format of the model, and examine th e effectiveness of t he u se of the model to track the development of each student’s creativity, in all four asp ects, as well as the entire clas s as a referenc e group. Due to space limitations full results of these studies are not included in this paper; however I would like to shed light on some of the insights gained from them: Types of Problem Posing Situations In their study, Stoyanova and Ellerton (1996) suggest that every problem posing situation can be classified as free, semi-structured or structured. Problem posing situation will be referred to as free “when students are asked to generate a problem from a given, contrived or naturalistic situation. Some directions may be given to prompt certain specific actions” (p. 519); as semi-structured “when students are given an open situation and are invit ed to expl ore the st ructure and to complete it by ap plying kn owledge, sk ills, concepts and relationships from their previous mathematical experiences”; and as structured “when problem-posing activities are based on a specific prob- lem” (p. 520). The above mentioned studies indicated that the teachers found that it was easier to implement the WIN strategy within a structured problem posing situation, especially due to Copyright © 2013 SciRe s . 436  A. SHRIKI Figure 3. An example of a personal graphical display of cumulative relat ive scores (t = task). lack of previous experience with posi ng mathematical problems. In their opinion, such situation generates “a firmer anchor to hang on”. There is still, however, a need for a prolonged wide- scale study aimed at examining the impact of the type of situa- tion on the development of students’ creativity. Appropriate n es s of the Pose d Probl ems There is one reservation concerning the “freedom” of posing new problems. Given that students are scored for fluency, the teachers noticed that they might be tempted to pose as many problems as possible, without considering their appropriateness. Inappropriate problems can have, for example, insufficient or irrelevant information. Namely, posing mathematical problem cannot stand as its own goal, and students must be explicitly instructed how to consider criteria such as appropriateness or correctness with regard to the requirements and constraints of the task (Andiliou & Murphy, 2010), and not implement a wa- tered down version of the approach in an effort to introduce “novel ideas.” Discussing the Essence of Original Problems In order to develop students’ appreciation to originality, the teachers found it important to present original problems that were posed by their fellow classmates, and spend time discuss- ing and negotiating issues that concern the essence of these problems. In their opinion, such discussion might shed light on distinctions between “regular problems” and “original prob- lems”, and, as suggested by Silver (1997), instruct students how to evaluate the novelty of a posed problem. Avoid Overemphasizing the Need to Solve the Posed Problems As mentioned, the WIN strategy can yield new and stimulat- ing problems that ultimately may result in some interesting in- vestigations. However, as ev iden t from t he f irst st udy m entioned above, overemphasizing th e need to solve the problems that were posed might suppressed the willingness to pose, what might be regarded as a “revolutionary problem”. In such cases, learners might hold back, concerned about their inability to solve the problems they themselves have posed (Lavy & Shriki, 2010). Therefore, in order not to ‘block’ the flow of problems posed by students, teachers should instruct them not to worry about their inability to solve some of the problem; otherwise they might li- mit themselves to posing trivial problems. Instead, solving “dif- ficult” problems might be done through a collaborative class effort. Students’ Self-Assessment of Their Progre ss As mentioned, learners’ self-assessment of one’s own crea- tivity enables them to refine their products in successive itera- tions (Chamberlin & Moon, 2005). Indeed, as was evident from the teachers’ and the students’ reflective portfolios, the graphi- cal displays of their gradual progress, as describe in Figure 3, was a powerful means that allowed them to reflect on their strengths and weaknesses as well as their progress over time, both relatively to their previous accomplishments and their re- ference group. It turned out that t he use of the model and “trans- lating” personal results into graphical display had a great im- pact on the teachers’ and students’ motivation to improve their fluency, flexibility and originality, as well as their drive to search for possible generalized problems. The Flexibility of the Model As mentioned, teachers are free to determine the upper limit for creativity as well as the relative weight of each component. In that sense, the model is rather flexible and actually enables teachers to adapt it to their teaching goals. As was evident from the first study mentioned above, the teachers attributed great importance to this flexibility. In their opinion organization, for example, should receive a low weight in cases where low achi- evers are engaged in problem posing, since they have difficul- ties in understanding the meaning of generalization. Originality, for example, should have a lower upper limit in classes of high achievers, in order to encourage them to pose unconventional problems. Therefore, as stated, it is important to leave the final decision in the hand of the teachers, allowing them to adjust the model to the target populations and their educational philoso- phy. Discussion and Conclusions In a changing technological society, innovations are recog- nized as the vehicle of economic and social growth and as es- sential to the welfare of all (Andiliou & Murphy, 2010). Pro- moting these innovations necessitates creativity (Shalley & Gil- son, 2004). When taken to its logical conclusion, and viewing creativity and content knowledge as inseparable (Rowlands, 2011), this implies that the objective of education should not be limited to enhancing knowledge and skills, but also to nurturing creativity (Craft, 2009). However, creativity is not often nur- tured in school (Sriraman, 2005). As has been mentioned in the introduction section, several cond itions ar e offer ed to justify this situation. This complex set of perceived obstacles suggests that attention should be given, first and foremost, to modifying tea- chers’ beliefs regarding the nature of creativity, as beliefs tea- chers hold regarding creativity are likely to influence the role they assume in relation to creative thinking as a learning objec- tive, the instructional approach they implement for fostering students’ knowledge and creative behavior in the subject matter being taught, and the evaluation procedures they apply in order to assess creative products (Andiliou & Murphy, 2010). A first step towards achieve this goal is to assist teachers to view crea- tivity as inherent in learning (Beghetto & Kaufman, 2009), and inspire teachers to believe that all students can become creative— as creativity is not an exclusive trait of the gifted (Rowlands, 2011). However, in order for teachers’ beliefs to translate into instructional practice, they have to establish the development of Copyright © 2013 SciRe s . 437  A. SHRIKI creative thinking as a discrete learning goal. In addition, atten- tion should be given to strengthen teach ers’ ability and readiness to nurture students’ creativity, and provide them with appropri- ate tools and pedagogic approaches aimed at supporting their capability to develop and assess students’ creativity. All of this must be done while taking into account constraints such as co- verage of the mandated curr iculu m and stand ardized testing out- comes. Although contemporary views o f creativity diff er with respect to the nature they ascribe to creativity and to the ability of indi- viduals to produce creative outcomes, there is a growing con- sensus regarding the centrality of problem posing and problem solving processes within the creative act (Silver, 1997). In order to enable studen ts to generat e their own mathem atical problems, Silver (1997) suggests employing the three-phase WIN instructional approach developed by Brown and Walter (1969, 1990). The third phase, posing new problems and ques- tions and subsequently solving at least one of them, are closely connected to creativity (Silver, 1997). By implementing this approach, teachers are likely to support the development of stu- dents’ creativity in mathematics. In addition, by discussing the posed problems students learn to evaluate the novelty of a pro- blem. According to Haylock (1986), mathematical assignments should include problem posing, problem solving, and redefini- tion. The WI N strategy approach inc ludes all three of thes e com- ponents. Therefore, it appears that implementing this approach systematicall y in cl asses might satisf y both develo ping studen ts’ mathematical creativity and effectively respond to the need to adhere to curricular demands within specific time limitations. Namely, the WIN approach guarantees that nurturing creativity does not come at the expense of teaching the subject matter, but rather completes it. For that matter, instead of askin g students to solve 10 different problems that do not have anything in com- mon, teachers might ask students to solve 10 different problems that can be derived from the same mathematical situation. In re- turn, arriving at conclusions and identifying generalizations will strengthen students’ mathematic al and metamath ematical know- ledge (Lavy & Shriki, 2008; Shriki, 2010). In this paper I suggest a model for assessing students’ crea- tivity and i ts developm ent in the context of problem posing, with the aim to respond teachers’ need for having a coherent and ac- cessible tool to serve this purpose (Shriki, 2010). Reid and Pe- tocz (2004) state that “it is a fairly difficult exercise to discern what is meant by the term ‘creativity’, or to deci de wh at ma y be interpreted as a ‘creative’ object, or to describe the cognitive traits that characterize a ‘creative’ person” (p. 46). Therefore, the proposed model is based on measurable aspects of creativity, namely—fluency, flexibility, novelty and organization (Tor- rance, 1974; Silver, 1997). Viewing personal creativity as a qua- lity that can be developed in school students, there is a need to distinguish between relative and absolute creativity (Leikin, 2009). Thus, in the proposed model, e ach student receives a total as well as relative score of fluency, flexibility, originality and organization. As teachers’ beliefs about creativity influence how they define, operationalize, and evaluate students’ creativity (Andiliou & Murph y, 2010), it is import ant to let teachers d ecide what they perceive as the meaning of “originality” and how to weight of each of the measured aspects for calculating final scores of cre ativity. In th at sense, the model is rath er flexible and actually enables teachers to adapt it to their teaching goals. In addition, it is suggested to provide students’ with an ongoing feedback regarding their progress, preferably through a graphi- cal display of their accomplishments. Taking all together, it is hoped that with careful planning and implementation, a pedagogic approach that combines problem posing with the proposed model and students’ self- assessment of their progress will enhance the teacher’s ability to nurture stu- dents’ creativity and assess its development while taking into account constraints such as coverage of the mandated curriculum and standardized testing outcomes. There is still, however, a need for a wide scale experiment in order to be able to determine which of the four mentioned as- pects of creativity is more likely to be developed through prob- lem posing—that is, subject to observable outside influences, why and how. A wide scale experiment will als o en able to dee p- en the insights regarding the meaning of numerical indicators like averages an d standard deviations that can be derive from the model, and the ab il ity to interpre t them. Concluding Remarks This paper neither suggests any conclusive definition of creativity, nor an ultimate approach dictating how to nurture it. Teachers need to be provided with a wide variety of in- formation, tools, and resources in order to enable them to consolidate their world-view regarding these issues, and al- low them to decide which approach best suits their teaching goals, educational values and beliefs. Given that the final score of creativity does not provide specific information about the scores of each component, one might prefer to display the 4 relative scores and the fin al score of creativity in a format of a vector such as (R.S flu- ency, R.S fl exibil ity, R.S orig inal ity, R.S o rganiz ation, over - all crea tivity). The problem posing approach, through implementing the WIN strategy, can be adapted to all school disciples, and therefore the proposed model for assessing the development of creativity in the context of problem posing can be em- ployed by teachers from all content areas, and not exclu- sively by mathematics teachers. REFERENCES Aljughaiman, A., & Reynolds, E. (2005). Teachers’ conceptions of creativity and creative students. Journal of Creative Behavior, 39, 17-34. doi:10.1002/j.2162-6057.2005.tb01247.x Andiliou, A., & Murphy, K. P. (2010). Examining variations among researchers’ and teachers’ conceptualizations of creativity: A review and synthesis of contemporary research. Educational Research Re- view, 5, 201-219. doi:10.1016/j.edurev.2010.07.003 Balka, D. S. (1974). Creative ability in mathematics. Arithmetic Tea- cher, 21, 633-363. Beghetto, R. A. (2006). Creative justice? The relationship between pro- spective teachers’ prior schooling experiences and perceived impor- tance of promoting student creativity. The Journal of Creative Be- havior, 40, 149-162. doi:10.1002/j.2162-6057.2006.tb01270.x Beghetto, R. A., & Kaufnan, J. C. (2009). Do we all have multicreative potential? ZDM Mathematics Education, 41, 39-44. doi:10.1007/s11858-008-0143-7 Brandau, L. I., & Dossey, J. A. (1979). Processes involved in mathema- tical divergent problem-solving. San Francisco: American Educatio- nal Research Association. Brookhart, S., Andolina, M., Zuza, M., & Furman, R. (2004). Minute math: An action research study of student self-assessment. Educa- tional Studies in M athematics, 57, 213-227. doi:10.1023/B:EDUC.0000049293.55249.d4 Brown, S. I., & Walter, M. I. (1969). What if not? Mathematics Teach- Copyright © 2013 SciRe s . 438  A. SHRIKI Copyright © 2013 SciRe s . 439 ing, 46, 38-45. Brown, S. I., & Walter, M. I. (1990). The art of problem posing. Hills- dale, NJ: L. Erlbaum Associates. Chamberlin, S. A., & Moon, S. (2005). Model-eliciting activities: An introduction to gifted education. Journal of Secondary Gifted Educa- tion, 17, 37-47. Craft, A. (2001). Little c creativity. In A. Craft, B. Jeffrey, & M. Leib- ling (Eds.), Creativity in education. London: Continuum. Craft, A. (2009). Trusteeship, wisdom, and the creative future of educa- tion. http://www.abp.unimelb.edu.au/unesco/ejournal/pdf/craft.pdf Cunningham, R. (2004). Problem posing: An opportunity for increasing student responsibility. Mathematics and Computer Education, 38, 83-89. Ellerton, N. F., & Clarkson, P. C. (1996). Language factors in mathe- matics teaching and learning. In A. I. Bishop (Eds.), International handbook of mathematics education (pp. 987-1033). Alphen aan den Rijn: Kluwer Academic Publishers. Enz, B., & Serafini, F. (1995). Involving students in the assessment process. Teaching PreK-8, 25, 96-97. Feldman, D. H., & Benjamin, A. C. (2006). Creativity and education: An American retrospective. Cambridge Journal of Education, 36, 319-336. doi:10.1080/03057640600865819 Fryer, M. (1996). Creative teaching and learning. London: Paul Chap- man Publishing Ltd. Hall, L. D., Fisher, C., Musanti, S., & Halquist, D. (2006). Professional development in teacher education: What can we learn from PT3? Tech Trends, 50, 25- 31. doi:10.1007/s11528-006-7600-3 Haylock, D. W. (1986). Mathematical creativity in schoolchildren. Jour- nal of Creative Behavior, 21, 48-59. doi:10.1002/j.2162-6057.1987.tb00452.x Henry, J. (2009). Enhancing creativity with M.U.S.I.C. The Alberta Journal of Educational Research, 5, 199-211. Hönsberger, R. (1985). Mathematical gems III. The Mathematical As- sociation of America. Lavy I., & Shriki, A. (2008). Investigating changes in prospective tea- chers’ views of a “Good Teacher” while engaging in a computerized Project-Based-Learning. Journal of Mathematics Teacher Education, 11, 259-284. doi:10.1007/s10857-008-9073-0 Lavy, I., & Shriki, A. (2010). Engaging in problem-posing activities in a dynamic geometry setting and the development of prospective tea- chers’ mathematical knowledge. Journal of Mathematical Behavior, 29, 11-24. doi:10.1016/j.jmathb.2009.12.002 Leikin, R. (2009). Exploring mathematical creativity using multiple so- lution tasks. In R. Leikin, A. Berman, & B. Koich u (Eds .), Creativity in mathematics and the education of gifted students (pp. 129-145). Rotterdam: Sense Publisher. Lin, Y.-S. (2011). Fostering creativity through education—A concep- tual framework of creative pedagogy. Creative Education, 2, 149- 155. doi:10.4236/ce.2011.23021 Mann, E. L. (2006). Creativity: The essence of mathematics. Journal for the Education of the Gifted, 30, 236-260. Martinez-Cruz, A. M., & Contreras, J. N. (2002). Changing the goal: An adventure in problem solving, problem posing, and symbolic meaning with a TI-92. Mathematics Teacher, 95, 592-597. NACCCE (1999). All our futures: Creativity, culture and education, national advisory committee on creative and cultural education. London: DFEE. http://www.cypni.org.uk/downloads/alloutfutures.pdf NCTM—National Council of Teachers of Mathematics (2000). Princi- ples and standards for school mathematics. Reston, VA: NCTM. Plucker, J. A., Beghetto, R. A., & Dow, G. T. (2004). Why isn’t crea- tivity more important to educational psychologists? Potential, pitfalls, and future directions in creativity research. Educational Psycholo- gists, 39, 83-96. doi:10.1207/s15326985ep3902_1 Reid, A., & Petocz, P. (2004). Learning domains and the process of creativity. The Australian Educ ational Rese a rcher, 31, 45-62. doi:10.1007/BF03249519 Rowlands, S. (2011). Disciplinary boundaries for creativity. Creative Education, 2, 47-55. doi:10.4236/ce.2011.21007 Shalley, C. E., & Gilson, L. L. (2004). What leaders need to know: A review of social and contextual factors that can foster or hinder crea- tivity. Leadership Quarterly, 15, 33-53. doi:10.1016/j.leaqua.2003.12.004 Shriki, A. (2010). Working like real mathematicians: Developing pro- spective teachers’ awareness of mathematical creativity through gen- erating new concepts. Educational Studies in Mathematics, 73, 159- 179. doi:10.1007/s10649-009-9212-2 Silver, E. A. (1994). On mathematical problem posing. For the Learn- ing of mathematics, 14, 19-28. Silver, E. A. (1997). Fostering creativity through instruction rich in mathematical problem solving and problem posing. ZDM-The Inter- national Journal on Mathem at i c s Education, 29, 75-80. doi:10.1007/s11858-997-0003-x Smith, C. (1997). Student self-assessment at St. Bernadette’s primary school. Primary Educa t or , 3, 7-9. Sriraman, B. (2005). Are giftedness and creativity synonyms in mathematics? The Journal of Secondary Gifted Education, 17, 20-36. Stoyanova, E., & Ellerton, N. F. (1996). A framework for research into students’ problem posing. In P. Clarkson (Ed.), Technology in mathematics education (pp. 518-525). Melbourne: Mathematics Education Research G roup of Australasia. Torrance, E. P. (1974). The torrance tests of creative thinking: Techni- cal-norms manual. Bensenvi lle, IL: Scholastic Testing Services. Treffinger, D. J., Young, G. C., Selby, E. C., & Shepardson, C. (2002). Assessing creativity: A guide for education. Sarasota, FL: The Na- tional Research Center on the gifted and talented.
|