Journal of Electromagnetic Analysis and Applications, 2013, 5, 294-301
http://dx.doi.org/10.4236/jemaa.2013.57046 Published Online July 2013 (http://www.scirp.org/journal/jemaa)
Physical Interpretation of the Dirac Neutrino with
Electromagnetic Mass*
Héctor Torres-Silva
Escuela de Ingeniería Eléctrica Electrónica, Universidad de Tarapacá, Arica, Chile.
Received April 6th, 2013; revised May 6th, 2013; accepted May 14th, 2013
Copyright © 2013 Héctor Torres-Silva. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
The usual choice of an orthogonal set of four plane-wave solutions of the free-particle Dirac equation does not lend it-
self readily to direct and complete physical interpretation in the case of Dirac neutrino particle. A different choice of
solutions can be made which yields a direct physical interpretation at all energies. Besides the separation of positive and
negative energy states there is a further separation of states for which the spin is respectively parallel or antiparallel to
the direction of the momentum vector. This can be obtained from the Maxwell’s equation without charges and current
in the
E
H configuration. Scenery of our study is at high temperature T where coexist electron-positron pair and
neutrino-antineutrino pair, (i.e., ). Taking into consideration the possibility of negative mass, we can de-
scribe the observed behavior of antimatter in response to electromagnetic fields by assuming that the anti Dirac neutrino
has a negative mass, so a new causal symmetry can be obtained.
1MeVT
Keywords: Chiral Neutrino; Dirac Equation; Maxwell System
1. Introduction
Neutrino electromagnetic properties, which are the main
subject of this paper, are of particular importance be-
cause they provide a kind of bridge to “new physics”
beyond the standard model. In spite of reasonable efforts
in studies of neutrino electromagnetic properties, up to
now there is no experimental confirmation in favour of
non vanishing neutrino electromagnetic characteristics.
[1]. The group of elementary particles called neutrinos
(denoted by the greek letter “

”) belongs to the lepton
family (together with electrons, muons and tauons). They
are electrically neutral and travel close to the speed of
light. There are three (known) flavours, or types, of neu-
trinos, electron neutrino


e

, muon neutrino




and
tau neutrino



, all with their corresponding antiparti-
cles. All neutrino interactions are mediated by the weak
nuclear force (and of course gravitation) [2].
Electron neutrinos, muon neutrinos, and tau neutrinos
that can morph into one another. For example, when
cosmic rays strike the atmosphere, they create particles
called muons that decay much as neutrons do, to produce
muon neutrinos [3]. The muon neutrinos can then “oscil-
late” or “mix” into other flavors before reaching Earth, as
observed in 1998 by physicists using a detector Super-
Kamiokande in Japan. Electron neutrinos from the sun
also change flavor, as physicists at the Sudbury Neutrino
Observatory in Canada showed in 2001 [4].
This means that neutrinos interact weakly via the elec-
tromagnetic force at all, and this makes them very diffi-
cult to detect for us. The cross section of a typical neu-
trino is very small, and it is therefore able to pass though
ordinary matter very easily [5].
The mass of the neutrinos is not well known. Meas-
urements of the speed of neutrinos have failed to show
that they move slower than the speed of light, which in-
dicate no or an extremely small mass. However, evidence
for neutrino oscillation demands that neutrinos have
masses [6]. Neutrino oscillation enables neutrinos of one
flavour to change into another flavour. This happens with
a certain probability that is proportional to the difference
of the square of the masses. Since these flavour oscilla-
tions have been observed, neutrinos are believed to have
very small but non zero rest masses and that neutrinos
generally are relativistic (their energy is much larger than
their rest mass) [7].
*This work has been supported by the Proyecto Mayor 8731-13, 2013
of the Universidad de Tarapacá, Chile. In the course of the recent development of knowledge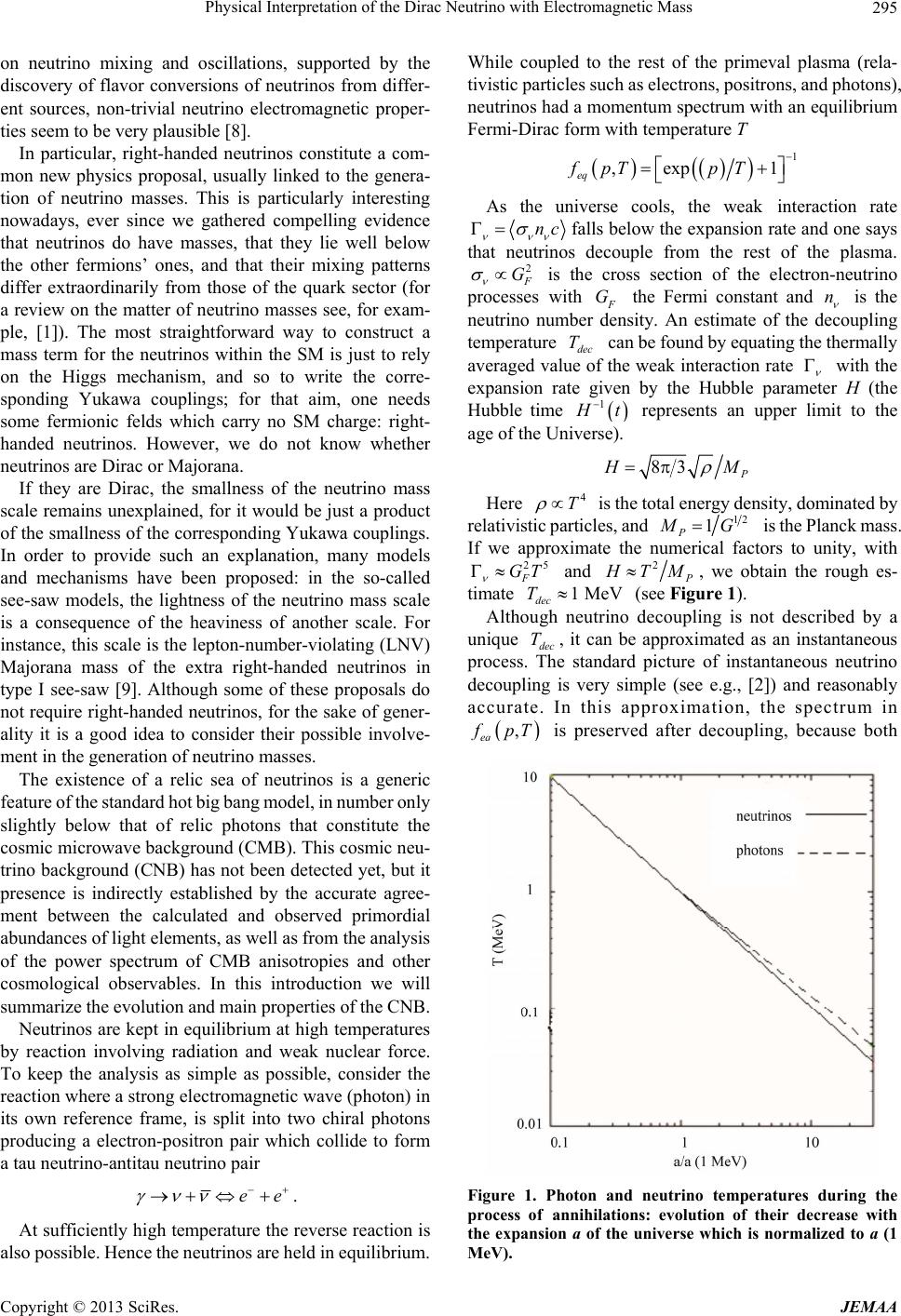

Physical Interpretation of the Dirac Neutrino with Electromagnetic Mass 295
on neutrino mixing and oscillations, supported by the
discovery of flavor conversions of neutrinos from differ-
ent sources, non-trivial neutrino electromagnetic proper-
ties seem to be very plausible [8].
In particular, right-handed neutrinos constitute a com-
mon new physics proposal, usually linked to the genera-
tion of neutrino masses. This is particularly interesting
nowadays, ever since we gathered compelling evidence
that neutrinos do have masses, that they lie well below
the other fermions’ ones, and that their mixing patterns
differ extraordinarily from those of the quark sector (for
a review on the matter of neutrino masses see, for exam-
ple, [1]). The most straightforward way to construct a
mass term for the neutrinos within the SM is just to rely
on the Higgs mechanism, and so to write the corre-
sponding Yukawa couplings; for that aim, one needs
some fermionic felds which carry no SM charge: right-
handed neutrinos. However, we do not know whether
neutrinos are Dirac or Majorana.
If they are Dirac, the smallness of the neutrino mass
scale remains unexplained, for it would be just a product
of the smallness of the corresponding Yukawa couplings.
In order to provide such an explanation, many models
and mechanisms have been proposed: in the so-called
see-saw models, the lightness of the neutrino mass scale
is a consequence of the heaviness of another scale. For
instance, this scale is the lepton-number-violating (LNV)
Majorana mass of the extra right-handed neutrinos in
type I see-saw [9]. Although some of these proposals do
not require right-handed neutrinos, for the sake of gener-
ality it is a good idea to consider their possible involve-
ment in the generation of neutrino masses.
The existence of a relic sea of neutrinos is a generic
feature of the standard hot big bang model, in number only
slightly below that of relic photons that constitute the
cosmic microwave background (CMB). This cosmic neu-
trino background (CNB) has not been detected yet, but it
presence is indirectly established by the accurate agree-
ment between the calculated and observed primordial
abundances of light elements, as well as from the analysis
of the power spectrum of CMB anisotropies and other
cosmological observables. In this introduction we will
summarize the evolution and main properties of the CNB.
Neutrinos are kept in equilibrium at high temperatures
by reaction involving radiation and weak nuclear force.
To keep the analysis as simple as possible, consider the
reaction where a strong electromagnetic wave (photon) in
its own reference frame, is split into two chiral photons
producing a electron-positron pair which collide to form
a tau neutrino-antitau neutrino pair
ee 

 .
At sufficiently high temperature the reverse reaction is
also possible. Hence the neutrinos are held in equilibrium.
While coupled to the rest of the primeval plasma (rela-
tivistic particles such as electrons, positrons, and photons),
neutrinos had a momentum spectrum with an equilibrium
Fermi-Dirac form with temperature T
  
1
,exp 1
eq
fpTpT 





As the universe cools, the weak interaction rate
nc  

falls below the expansion rate and one says
that neutrinos decouple from the rest of the plasma.
2
F
G  

is the cross section of the electron-neutrino
processes with
F
G the Fermi constant and n

is the
neutrino number density. An estimate of the decoupling
temperature dec can be found by equating the thermally T
averaged value of the weak interaction rate

 with the
expansion rate given by the Hubble parameter H (the
Hubble time


1
H
t
 represents an upper limit to the
age of the Universe).
83
P
H
M  
Here is the total energy density, dominated by
4
T  
relativistic particles, and 12 1
P
M
G is the Planck mass.
If we approximate the numerical factors to unity, with
25
GT
F 
and  2
P
H
TM, we obtain the rough es-
timate 1M
dec
TeV

(see Fi gure 1).
Although neutrino decoupling is not described by a
unique dec , it can be approximated as an instantaneous T
process. The standard picture of instantaneous neutrino
decoupling is very simple (see e.g., [2]) and reasonably
accurate. In this approximation, the spectrum in


f
,
eq pT is preserved after decoupling, because both
Figure 1. Photon and neutrino temperatures during the
process of annihilations: evolution of their decrease with
the expansion a of the universe which is normalized to a (1
MeV).

Physical Interpretation of the Dirac Neutrino with Electromagnetic Mass 296
neutrino momenta and temperature redshift identically
with the expansion of the universe. Shortly after neutrino
decoupling the temperature drops below the electron mass,
favouring annihilations that heat the photons. If one e
assumes that this entropy transfer did not affect the neu-
trinos because they were already completely decoupled, it
is easy to calculate the change in the photon temperature
before any annihilation and after the electron-posi- e
tron pairs disappear by assuming entropy conservation of
the electromagnetic plasma. Here, we quote the result
between T

and T

[2]
13 after
before
11 1.40102
4
TT
T
T









which is also the ratio between the temperatures of relic
photons and neutrinos.
One can see in Figure 1 how in this epoch the photon
temperature decreases with the expansion less than the
inverse of the scale factor . Instead the temperature of
the decoupled neutrinos always falls as
a
1a. Our interest
is to study the electromagnetic process for the conversion
ee 

 

at . This paper is
structured as follows. In Section 2 we start by reviewing
the Dirac equation under chiral representation. In Section
3 we obtain the Dirac equation deduced from Maxwell’s
equations with
1MeVT
E
H applied to neutrino at
which can provide light neutrino masses under a chiral
electromagnetic mechanism. Section 4 discusses the chi-
ral electromagnetic neutrino.
1MeVT
2. Chiral Dirac Neutrino Equation
Plane-wave solutions of the Dirac equation are well
known, and it would appear to be necessary to justify a
reconsideration of this problem related with Dirac neu-
trino particles. The justification lies in the fact that the
solutions found in journals and elsewhere do not lend
themselves readily to a direct physical interpretation. In
the usual treatment of the problem, four mutually or-
thogonal solutions are obtained for a given value of the
momentum p, two of which correspond to positive en-
ergy and two to negative energy. However, the physical
distinction between a pair of solutions belonging to the
same energy does not appear until one considers the low
energy approximation in which the small components of
the state function are neglected and the two solutions
reduce to eigenfunctions of
z

belonging to eigenval-
ues .
1
The original Dirac equation is

2
ˆˆ
cpmci t



   (1a)
where ψ = ψ(r, t) is a complex four-component field ψ
that Dirac thought of as the wave function for the electron,
r and t are the space and time coordinates, m is the rest
mass of the electron, is the momentum operator, c is
the speed of light speed, and is the reduced Planck
constant Planck (h/2π). Furthermore,
ˆ
p

ˆ

is a vector
operator whose components are 4 × 4 matrices:


123
ˆ,,

 , and

is another 4 × 4 matrix.
In the usual notation, the Dirac Hamiltonian for a free
particle is [10]
2
ˆˆ
H
cpmc

  . (1b)
This Hamiltonian commutes with the momentum vec-
tor , and the usual procedure is to seek simultaneous
eigenfunctions of H and p. These eigenfunctions are,
however, not uniquely determined, and for given eigen-
values of H and p, there remains a twofold degeneracy.
In order to resolve this degeneracy we seek a dynamical
variable which commutes with both H and . Such a
variable is
ˆ
p
ˆ
p
ˆˆ
p


, where ˆ

is the matrix Pauli. It is ob-
vious that this variable commutes with . To verify that
it also commutes with H, we write 11
ˆ
p
ˆˆˆ



, and
recalling that

commutes with operator ˆ

, we have



 
11
ˆˆ ˆˆˆˆˆˆ0 cpp pcp  

 , (2)
since 1

commutes with ˆ

.
We now proceed to find simultaneous eigenfunctions
of the commuting variables H, p and ˆˆ
p

. We have,
since the components of p commute,

22
ˆˆ pp 

, (3)
where p is the magnitude of the momentum vector. Thus
for a simultaneous eigenstate of and
ˆ
pˆˆ p


, the
value of ˆˆ
p


will be +p or –p, corresponding to states
for which the spin is parallel or antiparallel, respectively,
to the momentum vector.
A simultaneous eigenfunction of H and p will have the
form of a plane wave [10]




,exp, 1,2,3,4
jj
rtip rWtj    

, (4)
where
j

are the four components of the wave function
and
j

are four numbers to be determined. In the ar-
gument of the exponential function, p represents the ei-
genvalues of the components of the momentum for this
state and W the corresponding eigenvalue of H. The
possibility of positive mass and negative mass is for-
mally consistent with the positive and negative solutions
to the equations of the Special Theory of Relativity when
combined with quantum mechanics [11]. Then can
have either of the two values.
W

1
2
242 2
Wmccp . (5)
In Equation (5) is the relativistic momentum and
is the invariant mass. There are two solutions to
Equation (5); a positive solution and a negative solution.
p
m

Physical Interpretation of the Dirac Neutrino with Electromagnetic Mass 297
Dirac [11] described these as the “wanted” and “un-
wanted” solutions, respectively [12]. Pauli [13] consid-
ered that only the positive energy solutions had meaning.
By contrast, here in connection with Dirac neutrino we
interpret both the positive and negative energy solutions
to be real solutions that represent substances with posi-
tive mass and negative mass, respectively.
Antimatter was first detected by observing the tracks
left by positive electrons or positrons in cloud chambers
caused by the movement of particles with an apparent
charge-to-mass ratio

em

that was opposite in sign to
that of electrons [14-16]. Related to Dirac neutrino, as we
will show below, the anti Dirac neutrino could be de-
scribed as a negative mass and uncharged particle. To do
that, we now demand that
j

be also an eigenfunction
of ˆˆ
p

 belonging to one of the eigenvalues , say,
where . Employing the usual matrix representa-
tion for
p
p
ˆ
p

, we have
ˆˆ
z
xy
xy z
ppip
ppip p 






. (6)
In the above matrix,
x
p,
y
pand
z
p are operators,
but since this matrix is to operate on an eigenfunction of
p, the operators can be replaced by their eigenvalues. We
shall, without risk of confusion, use the same symbols for
the eigenvalues as for the corresponding operators.
The eigenvalue equation
ˆˆ pp
 
, (7)
yields the following four equations:




12
12
34
34
zxy
xy z
zxy
xy z
ppip p
pipp p
ppip p
pipp p
1
2
3
4








 

 

. (8)
These equations are satisfied by


12
34
,
,
xy z
xy z
pippp
pip pp
,
,


 
 
 
(9)
where

is a number still to be determined (The con-
sistency of the equations is readily verified, recalling that
).
pp
We now make use of the requirement that

be an
eigenfunction of H belonging to the eigenvalue .
Then
W

0WH  ; (10)
that is,

2
1ˆˆ 0Wc pmc
   

. (11)
In terms of chiral matrices ˆ

, in Equation (11)
we replace ˆˆ
p


by its eigenvalue to obtain


2
10Wcpmc


. (12)
On expansion, we obtain





2
12
2
21
2
34
2
43
Wc p mc
Wcpmc
Wcp mcc
Wcpmc


0
0
0
0



 
 
 
 
. (13)
This system of equations is the chiral Dirac equation


0
ch
imc


 

 (13’)
The condition EW

 ensures the consistency of
these equations. Comparing Equation (13) with Equation
(9), we find
2
2
Wcpmc
Wcp
mc
 
  . (14)
We can now write the components of

as follows:


exp
jj iprWth
 ,
(15)




where
j

is given by



1
2
3
4






2
2
,
,
,
.
xy
z
xy
z
pip
pp
Wcppipmc
Wcppp mc


 
 
(16)
Since can be given either of the two values W W

and , the two values
p p

, we have found for given p
four linearly independent plane wave solutions. It is eas-
ily verified that they are mutually orthogonal.
The physical interpretation of the solutions is now
clear. Each solution represents a homogeneous beam of
Dirac neutrino particles of definite momentum p, of defi-
nite energy, either W

, and with the spin polarized ei-
ther parallel or antiparallel to the direction of propagation.
This condition can be obtained if we consider the Max-
well’s equations under a chiral approach [17-19]. Solu-
tions
j

of Equations (9) and (16) are still undeter-
mined because we need to link them with chiral Maxwell
equations. In the next section, solutions
j

will be re-
lated with the chiral electrodynamics when
E
H.
3. Dirac Neutrino Equation Deduced from
Maxwell’s Equations with
E
H
Here we show that it is possible to transform the Max-
well equation from six real components to four complex
components and in this form to obtain two spinor equa-
tions in the Weyl or chiral representation. First, we will

Physical Interpretation of the Dirac Neutrino with Electromagnetic Mass 298
consider the Maxwell equations for a sourceless anisot-
ropic chiral homogeneous medium. Following [20,21],
with the time variation as:

1
tt c
T 

 and c T is
as a chiral parameter, the Maxwell’s equations without
charges are expressed as:

11
tc
rot T
c
 

H
E, (17)
0div E (18)

11
tc
rot T
c
 
E
H, (19)
0div H (20)
Here, , rot 

is the frequency and is the
light velocity. Application of rot to (17) and (19) allows
us to write the wave equation for
c
, 
E
 or
H
.


22
22
2
2
2
2 1
0.
c
tt
c
t
T
rot rotrot
cc
Trotrot
c
 
 



(21)
This chiral wave equation represents an equation of
fourth order. Here we consider the condition
22
22
1
c
T
ct






0
0
(22)
where Equation (21) is transformed from a fourth order
equation to a first order one.

2
c
Trot (23)
and the electric field is parallel to the magnetic field
i
E
H. The linear Beltrami Equation (23), will be used
to construct the Dirac neutrino equation in chiral or Weyl
representation.
In [14], it was shown that the ordinary Dirac equation
is equivalent to the chiral quaternionic equation

0
cc
DD   


with 3

1
1
:
cD
ic mc

1



  and the Maxwell Eq-
uations (17)-(22) are equivalent to the chiral Equation
(23) when the electric field
E
is parallel to the mag-
netic field
H

i
E
H. Multiplying Equation (23) by
ˆ
i

we have

ˆˆ
20
c
iTirot   
that is, with 0




ˆˆ
ˆ
20
c
iT    .
From this equation we can separate

ˆˆˆ 20
cc
iT T   EE ,0
,0

ˆˆ
ˆ
20
cc
iT T   HH
Let


ˆˆ ,
RL
iE iH  

,



T
10 ,
and making ,1
tc
iTc



 and 2
c
Tmc we
obtain


1
0ˆ
R
L
ic mc
 
 (24)


1
0ˆ
L
R
ic mc

 . (25)
Equations (24) and (25) are equivalent to the quarter-
nionic chiral Dirac equation obtained in reference [14],
here
D
mm

is the Dirac neutrino mass. Solutions of
(24) and (25) may be called the Beltrami fields (see, e.g.,
[21]). R and L, subscripts are associated with circularly
polarized photons (right or left-handed spirals or chiral
photons), that is photons that have closed trajectories to
form standing waves that generate mass. The Dirac neu-
trino equation in chiral or Weyl representation is [15],

0
ch
imc




 (26)
In the chiral Dirac neutrino field

T
,
RL

,
R

and
L

are two different types of 2-component spinor,
they respectively correspond to the nonequivalent repre-
sentations (1/2, 0) and (0, 1/2) of the Lorentz group, and
the chiral Dirac neutrino equation presents a relation be-
tween the two spinors. If we consider parity, then it is no
longer sufficient to consider the 2-component spinors
R

and
L

separately, but the 4-component spinor
This 4-component spinor is an irreduci-
ble representation of the Lorentz group extended by par-
ity (i.e., the (1/2, 0) ⊕ (0, 1/2) representation).



T
,
RL
 .
Now we are in conditions of compare Equation (13’)
with Equation (26) and show that the dirac neutrino par-
ticle with mass generated by the
E
H configuration.


2
2
xy
z
xy
z
EE
E
cEE
Wmc
cEE
Wmc












 


E
E
E
(27)
where the electric field is given by 2
Wmc
e


E and
W



T
.
As c is positive or negative we can generalize the
product c as pT 2
c
pT

. For a massive Dirac neu-
trino, the electric and magnetic fields are 90˚ out of phase,
the energy density is constant and proportional to


222 2
0
44Gk   EH2 F

.
We find in SI units, that
. Here c is the critical
field for neutrino-antineutrino pair equivalent to the elec-
tron-positron pair production given by

2
2291 1
0
41.310
c
kFEEm

 E

Physical Interpretation of the Dirac Neutrino with Electromagnetic Mass 299
23 11181
1.3 10 Vm
ce
Emce
 
 . (28)
That is equivalent to . Observations indi-
cate that neutron stars have magnetic fields higher than
so neutrino-antineutrino pair is generated. In this
form we have a close connection between the Dirac neu-
trino equation and the Maxwell’s equation, with a direct
and complete physical interpretation in the
12
1.310G
12
10 G
E
H
T
con-
figuration. Here we are obtained a clear connection be-
tween the Planck constant , the quiral factor c, and
the electromagnetic mass which can be positive or nega-
tive according to .

c
It is well known that matter and antimatter respond to
electromagnetic radiation in opposite ways. For example,
if an electron (Dirac neutrino) moves one way in an elec-
tromagnetic field, a positron (Dirac anti neutrino) will
move in the opposite way. We apply our theory of posi-
tive and negative mass to matter and antimatter and sug-
gest that it is productive to consider matter as having a
positive mass (+chirality) and antimatter as having a
negative mass (−chirality). The equations presented here,
which treat matter as having a positive mass and anti-
matter as having a negative mass, can account for the
experimental observations of matter and antimatter in
chiral electromagnetic fields. Our treatment allows the
symmetry between matter and antimatter to be treated in
a more causal manner.
T
Taking into consideration the possibility of negative
mass, we can describe the observed behavior of antimat-
ter in response to electromagnetic fields by assuming that
the positron (anti Dirac neutrino) has a negative mass.
Given that particles and antiparticles respond oppositely
to an input of various forms of electromagnetic energy,
we considered the possibility that the mass can be con-
sidered in a causal symmetry. Taking into account the
concept of relative time, particularly the relativity of the
direction of time to describe antimatter, we now suggest
a more causal symmetry between matter and antimatter.
That is, instead of using CPT symmetry [22], where
matter is antisymmetrical with antimatter in terms of its
charge (C), parity (P) and direction in time (T), we sug-
gest that matter is antisymmetrical with antimatter in
terms of its mass, parity and time.
part conjantipart
M
PT MPT . (29)
So the combined MPT operations leaves invariant the
Dirac Equation (1)




2
2
:
ˆˆ
ˆˆ
particle
MPT
cpmci t
cpmc it







 



(30)
In the chiral representation also can be show that the
Dirac neutrino equation is invariant.
4. Chiral Electromagnetic Neutrino
Dirac introduced the concept of antiparticles, [23]. Now
we know that for every particle there is an antiparticle.
However some particles could be self-conjugate, in the
sense that particle and antiparticle could be the same. Of
course such particles have to be electrically neutral.
The possibility of a self-conjugate fermion was first
pointed out by Majorana [24], and hence they are called
Majorana fermions while the other fermions (with dis-
tinct particles and antiparticles) are called Dirac fermions,
Equations (24) and (25) [25]. Among the fermions of the
Standard Model, only neutrinos are electrically neutral
and hence qualify to be Majorana particles. But it is still
an open question whether neutrinos are Majorana parti-
cles or Dirac particles. In our theory we can discriminate
this situation if 1 2
c
Tmc


 with ,
M
RL
mm or
3
2
c
Tmc


 with
D
mm

respectively.
If neutrinos are Majorana particles, lepton number L is
not conserved and this opens the door to generate an ex-
cess of leptons over antileptons in the early universe
which can subsequently generate an excess of baryons
over antibaryons, thus explaining how after annihilation
of most of the particles with antiparticles, a finite but
small residue of particles was left, to make up the present
Universe.
Equations (24) and (25) support the see-saw mecha-
nism to explain why the neutrino masses, although not
zero, are so tiny.The seesaw mechanism is a generic
model used to understand the relative sizes of observed
neutrino masses, of the order of eV. See‐saw mechanism
maybe the reason for the smallness of the masses.
*Provides an explanation for the smallness of the neu-
trino masses;
*0
L
m


is natural, since a
L

mass term is forbid-
den by the SM symmetries;
*
D
m, generated by the Higgs mechanism can be taken
the order of the charged lepton masses;
*
R
m is not “protected” by the SM symmetries, and
can be taken large.
With our theory, using Equations (24) and (25) it is
possible to obtain a matrix mass
LD
D
R
mm
mm







. (31)
If with 1eVm


R
D we obtain two Majo-
rana particles, an electron neutrino light and a
sterile heavy one
mm

1eV



1TeV
R. In addition to the non-
zero neutrino masses and mixing angles, the nonzero
magnetic moment
m


is another property of neutrinos
beyond the standard model of particle physics. The im-

Physical Interpretation of the Dirac Neutrino with Electromagnetic Mass 300
portance of


was first mentioned by Pauli [18]. Sys-
tematic theoretical studies of neutrino electromagnetic
properties started after it was shown that in the extended
Standard Model with right-handed neutrinos the mag-
netic moment of a massive neutrino is, in general, non-
vanishing and that its value is determined by the neutrino
mass [26].
If neutrinos have a nonzero magnetic moment, it leads
to precession between left and right-handed neutrinos in
sufficiently strong magnetic fields [27]. In general,
nondiagonal elements of the magnetic moment matrix are
possible and neutrinos can be changed into different fla-
vours and chiralities, see Equations (24) and (25). Fur-
thermore, with the additional effect of coherent forward
scattering by matter, neutrinos can be resonantly con-
verted into those with different chiralities.
For a neutrino mass smaller than 1 eV, a Dirac neu-
trino has a non-zero magnetic moment proportional to
the neutrino mass, that yields a very small value for the
magnetic moment, 19 310




. As 2em



.
From our theory, the Bohr magneton is proportional to
c so in this case we have T8
10
c 
 Tecm

). From
data obtained of astrophysics (considering the cooling of
red giant stars), we obtain
12 11
3 103 100.1
c
Tm



 
corresponding to neutrino


. There is a gap of some
orders of magnitude between the present experimental
limits 11 12 10 10




15
10

 [28], on neutrino magnetic
moments and the predictions of different extensions of
the Standard Model which hint at a range
14
10




 [29]. The main problem in distin-
guishing Dirac from Majorana neutrino is the lack of
neutrino with positive helicity. One way is to reverse the
spin of the neutrino in an external magnetic field. The
problem is that we need large neutrino magnetic mo-
ments and large magnetic field to obtain visible effects.
However with our theory it is possible to reverse the spin
using laser technology to have sufficient energy density
to generate Dirac neutrino [30].




2
22291
41.310
ei
HEE m 


 GE
ei
.
Here ei is the critical field for electron positron
production
E18 1
1.3 10EVm


T
. We think that by mea-
suring the chirality c of the processes, we may have an
improvement in the study of electromagnetic properties
of neutrinos.
An example is the modeling of neutrinos propagation
during core-collapse supernovae where very strong mag-
netic fields are believed to exist and in which the influ-
ence of neutrino electromagnetic properties has not yet
been taken into account. Equation (24) is well suited to
study the electromagnetic properties of neutrinos and
Majorana particles such as charge conjugation and time
reversal, allowing for an experimental study of our Equa-
tions (24)-(26).
5. Conclusions
The two-component Dirac neutrino equation, coming in
two related forms (24) and (25) that are connected by a
spin flip, represents the simplest possible covariant rela-
tivistic wave equation for a massive fermion. These two
forms represent the two irreducible representations of the
Lorentz group in terms of Pauli spinors and matrices.
Also the Dirac neutrino equation can directly be derived
by linearization of Equation (8), a procedure which leads
to (24) and (25) without explicit recourse to the Dirac
theory. An important characteristic of neutrino electro-
magnetic properties is that they are different from Dirac
and Majorana neutrinos. In particular, Majorana neutri-
nos cannot have diagonal magnetic or electric moments.
Thus, studies of neutrino electromagnetic interactions
from Equations (24) and (25) can be used as a procedure
to distinguish whether a neutrino is a Dirac or Majorana
particle.
Moreover, CP invariance in the lepton sector puts ad-
ditional constraints on the neutrino form factors and can
be tested with experimental probes of neutrino electro-
magnetic interactions.
REFERENCES
[1] G. Drexlin, et al., “Current Direct Neutrino Mass Ex-
periments,” Advances in High Energy Physics Vol. 2013,
2013, Article ID: 293986. doi:10.1155/2013/293986
[2] J. Lesgourgues and S. Pastor, “Massive Neutrinos and
Cosmology,” Physics Reports, Vol. 429, No. 6, 2006, pp.
307-379. doi:10.1016/j.physrep.2006.04.001
[3] A. Cho, “The Sterile Neutrino: Fertile Concept or Dead
End?” Science, Vol. 334, No. 6054, 2011, pp. 304-306.
doi:10.1126/science.334.6054.304
[4] D. V. Forero, M. Tortola and J. W. F. Valle, “Global
Status of Neutrino Oscillation Parameters after Neutrino-
2012,” Physical Review D, Vol. 86, No. 7, 2012, Article
ID: 073012.. doi:10.1103/PhysRevD.86.073012
[5] G. L. Fogli, E. Lisi, A. Marrone, D. Montanino, A. Palaz-
zo and A. M. Rotunno, “Global Analysis of Neutrino
Masses, Mixings, and Phases: Entering the Era of Lep-
tonic CP Violation Searches,” Physical Review D, Vol. 86,
No. 1, 2012, Article ID: 013012.
[6] M. C. Gonzalez-Garcia and M. Maltoni, “Phenomenology
with Massive Neutrinos,” Physics Reports, Vol. 460, No.
1-3, 2008, pp. 1-129. doi:10.1016/j.physrep.2007.12.004
[7] A. G. Cohen, S. L. Glashow and Z. Ligeti, “Disentangling
Neutrino Oscillations,” Physics Letters B, Vol. 678, No. 2,
2009, pp. 191-196. doi:10.1016/j.physletb.2009.06.020
[8] Z. Maki, M. Nakagawa and S. Sakata, “Remarks on the
Unified Model of Elementary Particles,” Progress of

Physical Interpretation of the Dirac Neutrino with Electromagnetic Mass 301
Theoretical Physics, Vol. 28, No. 5, 1962, pp. 870-880.
doi:10.1143/PTP.28.870
[9] J. W. F. Valle, “Neutrino Physics Overview,” Journal of
Physics: Conference Series, Vol. 53, No. 1, 2006, p. 473.
doi:10.1088/1742-6596/53/1/031
[10] S. M. Neamtan, “On the Physical Interpretation of Solu-
tions of the Dirac Equation for a Free Particle,” American
Journal of Physics, Vol. 20, No. 7, 1952, pp. 450-451.
doi:10.1119/1.1933275
[11] P. A. M. Dirac, “A Theory of Electrons and Protons,”
Proceedings of the Royal Society A, Vol. 126, No. 801,
1930, pp. 360-365. doi:10.1098/rspa.1930.0013
[12] P. A. M. Dirac, “Theory of Electrons and Positrons,”
Nobel Lecture, December 12, 1933.
[13] W. Pauli, “The Connection between Spin and Statistics,”
Physical Review, Vol. 58, No. 8, 1940, pp. 716-730.
doi:10.1103/PhysRev.58.716
[14] C. D. Anderson, “The Apparent Existence of Easily Def-
lectable Positives,” Science, Vol. 76, No. 1967, 1932, pp.
238-239. doi:10.1126/science.76.1967.238
[15] C. D. Anderson, “The Positive Electron,” Physical Re-
view, Vol. 43, 1933, pp. 491-494.
doi:10.1103/PhysRev.43.491
[16] C. D. Anderson, “The Discovery of Antimatter,” World
Scientific, Singapore, 1999.
[17] C. Chu and T. Ohkawa, “Transverse Electromagnetic
Waves with E B” Physical Review Letters, Vol. 48, 1982,
pp. 837-838. doi:10.1103/PhysRevLett.48.837
[18] H. Zaghloul, H. A. Buckmaster and K. Volk, “Comment
on ‘Invariants of the Electromagnetic Field and Electro-
magnetic Waves’,” American Journal of Physics, Vol. 56,
No. 3, 1988, p. 274. doi:10.1119/1.15664
[19] H. Torres-Silva, “Chiral Transverse Electromagnetic
Standing Waves with E II H in the Dirac Equation and the
Spectra of the Hydrogen Atom,” In: A. Akdagli, Ed., Be-
havior of Electromagnetic Waves in Different Media and
Structures, Book Intech, 2011, pp. 301-324.
[20] H. Torres-Silva and D. Torres, “Chiral Current in a Gra-
phene Battery,” Journal of Electromagnetic Analysis and
Applications, Vol. 4, No. 10, 2012, pp 426-431.
doi:10.4236/jemaa.2012.410059
[21] H. Torres-Silva, “Chiral Dirac Equation Derived from
Quaternionic Maxwell’s Systems,” Journal of Electro-
magnetic Analysis and Applications, Vol. 5, No. 3, 2013.
doi:10.4236/jemaa.2013.53017
[22] C. Itzykson and J.-B. Zuber, “Quantum Field Theory,”
McGraw-Hill, New York, 1980.
[23] P. M. A. Dirac, “The Quantum Theory of the Elec tron,”
Proceedings of the Royal Society of London. Series A,
Containing Papers of a Mathematical and Physical Cha-
racter, Vol. 117, No. 778, 1928, pp. 610-617.
[24] E. Majorana, “Teoria Simmetrica Dell’ Elettrone E Del
Positrone,” Il Nuovo Cimento, Vol. 14, No. 4, 1937, pp.
171-184. doi:10.1007/BF02961314
[25] W. Pauli, “Zur Quantenmechanik des Magnetischen Ele-
ktrons,” Zeitschrift für Physik A Hadrons and Nuclei, Vol.
43, No. 9-10, 1927, pp. 601-623.
doi:10.1007/BF01397326
[26] C. Giunti and C. W. Kim, “Fundamentals of Neutrino
Physics and Astrophysics,” Oxford University Press, Ox-
ford, 2007.
[27] S. Bilenky, “Introduction to the Physics of Massive and
mixed Neutrinos,” Lecture Notes in Physics, Vol. 817,
2010. doi:10.1007/978-3-642-14043-3
[28] N. F. Bell, et al., “How Magnetic Is the Dirac Neutrino?”
Physical Review Letters, Vol. 95, No. 15, 2005, Article
ID: 151802. doi:10.1103/PhysRevLett.95.151802
[29] A. Studenikin, “Neutrino Magnetic Moment,” Nuclear
Physics B, Vol. 188, 2009, pp. 220-222.
doi:10.1016/j.nuclphysbps.2009.02.053
[30] E. Fermi and C. N. Yang, “Are Mesons Elementary Parti-
cles?” Physical Review, Vol. 76, No. 12, 1949, pp. 1739-
1743. doi:10.1103/PhysRev.76.1739