Journal of Electromagnetic Analysis and Applications, 2013, 5, 271-280
http://dx.doi.org/10.4236/jemaa.2013.57043 Published Online July 2013 (http://www.scirp.org/journal/jemaa)
271
Analysis of Conservative and Magnetically Induced
Electric Fields in a Low-Frequency Birdcage Coil*
Bu S. Park1#, Sunder S. Rajan1, Christopher M. Collins2, Leonardo M. Angelone1
1Division of Physics, Center for Devices and Radiological Health, Office of Medical Products and Tobacco, Food and Drug Admini-
stration, Silver Spring, USA; 2Department of Radiology, New York University, New York, USA.
Received May 16th, 2013; revised June 17th, 2013; accepted June 25th, 2013
Copyright © 2013 Bu S. Park et al. This is an open access article distributed under the Creative Commons Attribution License, which
permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
Numerical methods are used to evaluate variations of the electromagnetic fields generated by a head-sized birdcage coil
as a function of load (“loading effect”). The loading effect was analyzed for the cases of a coil loaded with a conductive
cylindrical sample, a dielectric cylindrical sample, and an anatomically precise head model. Maxwell equations were
solved by means of finite difference time domain (FDTD) method conducted at 12.8, 64, and 128 MHz. Simulation
results indicate that at 12.8 MHz the conservative electric field


c
E
caused by the scalar electric potentials between
the coil and the load or within the load was significantly higher than the magnetically-induced electric field


i
E
and
was the major component of the total electric field


total
E. The amplitudes of c
E
and are seen to be lower
within a sample than at a corresponding location in an empty coil, but approximately 65% higher in the space between
coil and sample than at a corresponding location in an empty coil. This is due to polarization effects generating an addi-
tional scalar potential parallel to the original field. The increased electric field between coil and sample may cause in-
creased power deposition at the surface of the sample and may affect the RF-induced currents in external leads used for
physiological recording, i.e. ECG, during MRI scanning.
total
E
Keywords: MRI; FDTD; Loading Effect; Conservative Electric Field; Birdcage Coil
1. Introduction
In magnetic resonance imaging (MRI), the signal to noise
ratio (SNR) and the specific energy absorption rate
(SAR), the dosimetric parameter used to establish safety
limits for human subjects by the International Electro-
technical Commission (IEC) [1] and the US Food and
Drug Administration [2], depend upon the total electric
field


total
E. The total can be decomposed into a con-
servative and magnetically-induced electric fields (E-
fields) [3] and a distinction is often needed between the
two components. Conservative E-fields
E


c
E
caused by
the scalar electrical potential on conductors give rise to a
portion of sample loss also referred to as “dielectric loss”
[4]. Magnetically-induced E-fields i

E
are created by
the time-varying magnetic fields [5], and give rise to a
portion of sample loss also referred to as “inductive loss”
[4]. In some cases it is possible to reduce the losses due
to c
E
without changing the current distribution or
magnetic field distribution using a so called “Ec-shield”
[6], and thus maintaining the desired sensitivity and field
of view (FOV) while reducing SAR in the sample and/or
the noise received from the sample [6-9]. A previous
study [6] showed that this method could be applied to a
solenoid coil. This study evaluated whether the method
of “Ec-shield” could be also extended to a birdcage coil,
the most common type of coil used in human MRI. One
of the motivations of this study to understand the mecha-
nism of thermal injury to skin is currently the most
common type of adverse event reported for MRI scans
[10]. Another reason for this study is to find the effect of
a conductive or a dielectric sample related to the safety
assurance in a region of interest (ROI), particularly be-
tween the RF coil and the sample. Previous research
[9,11] showed that the total electric field inside a coil
would be decreased with addition of a loading sample.
*Disclaimer: The mention of commercial products, their sources, or
their use in connection with material reported herein is not to be con-
strued as either an actual or implied endorsement of such products by
the Department of Health and Human Services.
#Corresponding author.

Analysis of Conservative and Magnetically Induced Electric Fields in a Low-Frequency Birdcage Coil 272
Conversely, the hypothesis driving the proposed study
was that the electric field decreases only within the load-
ing sample, but it is the same or higher in the space be-
tween coil and sample. Changes in electric field between
coil and sample may cause increased power deposition in
the subject skin, with possible related thermal injury [10].
Moreover, changes in electric field may also affect the
RF-induced currents in external leads used for physio-
logical recording during MRI (e.g., ECG or EEG leads).
Additionally, there have been some suggestions that c
E
may play a significant role in the total sample loss, al-
though it is generally believed that almost all of the sample
loss is magnetically-induced [12].
The study was conducted by means of numerical simu-
lations conducting a systematic analysis of the electro-
magnetic field, including c
E
and i
E
generated by the
birdcage coil within and surrounding the load. The study
took advantage of a recently developed method based on
quasi-static approximation that allows separating nu-
merically-calculated E-field distributions into conserva-
tive and magnetically-induced portions [3]. We performed
numerical electromagnetic field simulations within and
surrounding a high pass (HP) birdcage coil combined with
a cylindrical conductive phantom and a human head
model at different frequencies. Additionally, the volume
charge density (ρυ) distribution generating the scalar elec-
tric potential and c
E
was calculated to support the ex-
planation of electromagnetic field variations. Results were
analyzed to evaluate the contribution of c
E
, i
E
and RF
magnetic field to the total electromagnetic field
distribution.

1
B
Conservative and Magnetically-Induced
Electric Field
The power loss (P) can be calculated as [8]:
2
1d
2total
vol
PE  v
(1)
where σ is the conductivity (S/m) and total total EE is
the amplitude of the total electric field


total
E (V/m),
which can be separated as two components:
totali c
t




A
E
EE
(2)
where
A
is the vector magnetic potential (Wb/m) and

is the scalar electric potential (V), respectively. In
order to reduce the total power absorbed by the sample,
the Etotal should be minimized, which means minimizing
the components c
E
and/or i
E
.
2. Materials and Methods
2.1. Birdcage Head Coil
A high-pass (HP) birdcage head coil was modeled using
12 rods of 300 mm of length, disposed circularly with an
inner diameter (ID) of 290 mm. To accurately simulate
the field distribution generated by an ideal high-pass
birdcage coil, 12 sinusoidal voltage sources of 1 V am-
plitude in series with a 50 Ω resistor were placed in both
the top and bottom rings, in the middle of each of the
segments between the rods of the coil (Figure 1). Each
source was assigned a phase-shift equal to the azimuthal
position of the segment (i.e., 30˚C) between voltages in
adjacent end ring segments, and with sources in opposite
end rings having opposite orientation. The following
frequencies were modeled: 12.8, 64, and 128 MHz, cor-
responding to 0.3, 1.5 and 3.0 T for water proton MRI.
2.2. Load: Phantom and Head Model
The birdcage head coil was loaded with a cylindrical
sample having ID of 200 mm and length of 300 mm with
a 5 mm resolution. Three different electrical properties
for the phantom were simulated, namely: a) conductive
sample (σ = 0.2 S/m, εr = 1), b) dielectric sample (σ = 0
S/m, εr = 78), and weak saline (σ = 0.2 S/m, εr = 78) [6].
Simulations were also performed with an anatomi-
cally-precise human head model (Figure 1). The human
head model was created by segmenting the digital photo-
graphic data of the National Library of Medicine’s Visi-
ble Human Project [13, 14], and then transforming these
segmented images into a 3D grid of Yee cell cubes [15].
The human head model had a 5 × 5 × 5 mm3 isotropic
resolution and contained 20 tissue types [16,17] having
different conductivity (σ) and relative permittivity (εr)
values.
2.3. Numerical Simulations and Data Processing
All simulations were performed using commercially
available software (xFDTD, Remcom, Inc, State College,
PA) and analysis of results was performed in Matlab
(The MathWorks, Inc., Natick, MA). Simulation results
of electromagnetic fields were normalized so that
14T


B at the coil center corresponding to a 1.5 ms
(a) (b)
Figure 1. Geometry of high pass (HP) birdcage coil (yellow),
sample (green, (a)) and head model (b) used for numerical
simulations.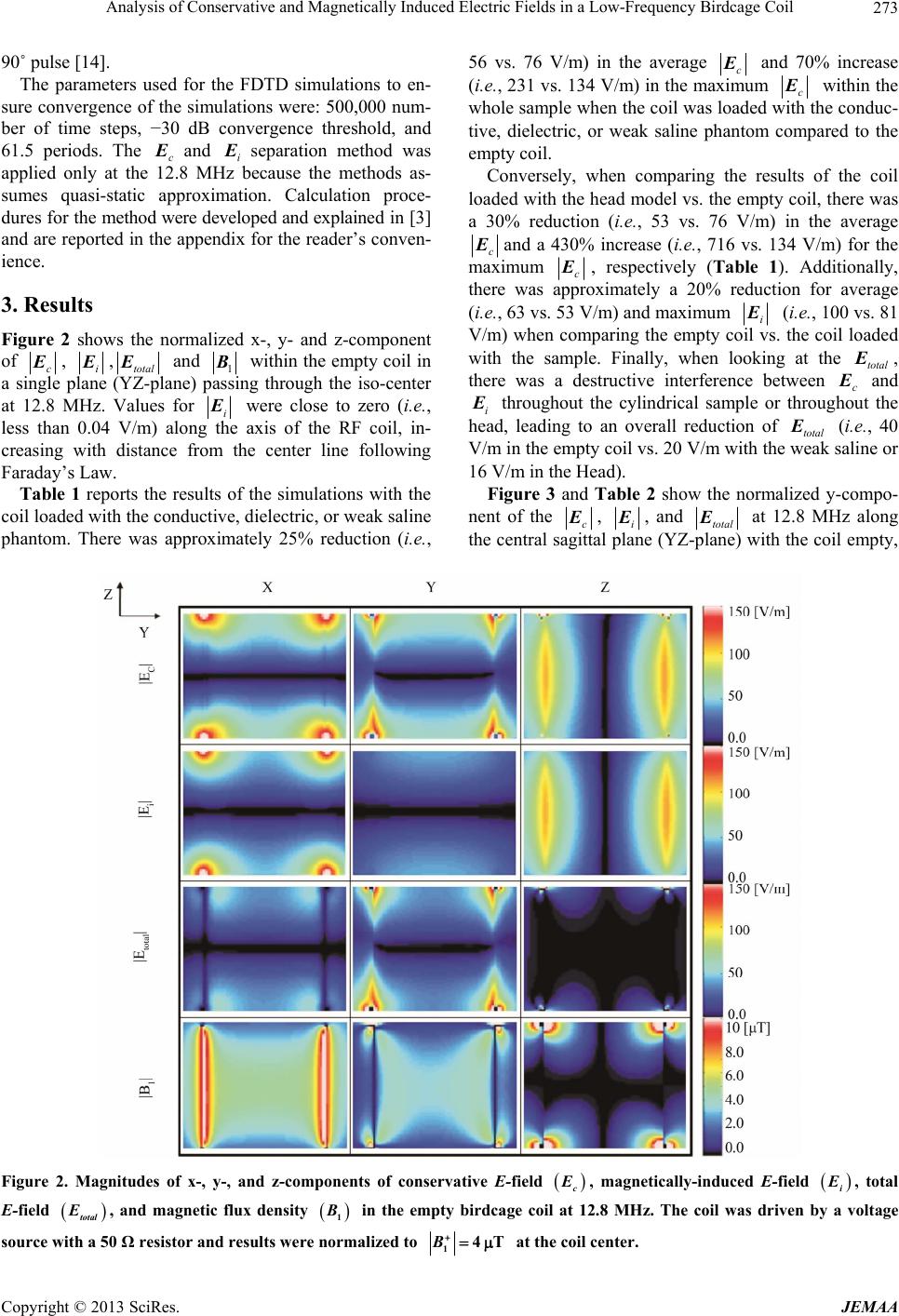

Analysis of Conservative and Magnetically Induced Electric Fields in a Low-Frequency Birdcage Coil 273
90˚ pulse [14]. 56 vs. 76 V/m) in the average c
E
and 70% increase
(i.e., 231 vs. 134 V/m) in the maximum c
E
within the
whole sample when the coil was loaded with the conduc-
tive, dielectric, or weak saline phantom compared to the
empty coil.
The parameters used for the FDTD simulations to en-
sure convergence of the simulations were: 500,000 num-
ber of time steps, −30 dB convergence threshold, and
61.5 periods. The c
E
and i
E
separation method was
applied only at the 12.8 MHz because the methods as-
sumes quasi-static approximation. Calculation proce-
dures for the method were developed and explained in [3]
and are reported in the appendix for the reader’s conven-
ience.
Conversely, when comparing the results of the coil
loaded with the head model vs. the empty coil, there was
a 30% reduction (i.e., 53 vs. 76 V/m) in the average
c
E
and a 430% increase (i.e., 716 vs. 134 V/m) for the
maximum c
E
, respectively (Table 1). Additionally,
there was approximately a 20% reduction for average
(i.e., 63 vs. 53 V/m) and maximum i
E
(i.e., 100 vs. 81
V/m) when comparing the empty coil vs. the coil loaded
with the sample. Finally, when looking at the total ,
there was a destructive interference between c
E
E
and
i
E
throughout the cylindrical sample or throughout the
head, leading to an overall reduction of total (i.e., 40
V/m in the empty coil vs. 20 V/m with the weak saline or
16 V/m in the Head).
E
3. Results
Figure 2 shows the normalized x-, y- and z-component
of c
E
, i
E
,total
E and 1 B within the empty coil in
a single plane (YZ-plane) passing through the iso-center
at 12.8 MHz. Values for i
E
were close to zero (i.e. ,
less than 0.04 V/m) along the axis of the RF coil, in-
creasing with distance from the center line following
Faraday’s Law.
Figure 3 and Table 2 show the normalized y-compo-
nent of the c
E
, i
E
, and total
E at 12.8 MHz along
the central sagittal plane (YZ-plane) with the coil empty,
Table 1 reports the results of the simulations with the
coil loaded with the conductive, dielectric, or weak saline
phantom. There was approximately 25% reduction (i.e.,
Figure 2. Magnitudes of x-, y-, and z-components of conservative E-field


c
E
, magnetically-induced E-field


i
E
, total
E-field , and magnetic flux density in the empty birdcage coil at 12.8 MHz. The coil was driven by a voltage
source with a 50 Ω resistor and results were normalized to

total
E

B1
B14T


 at the coil center.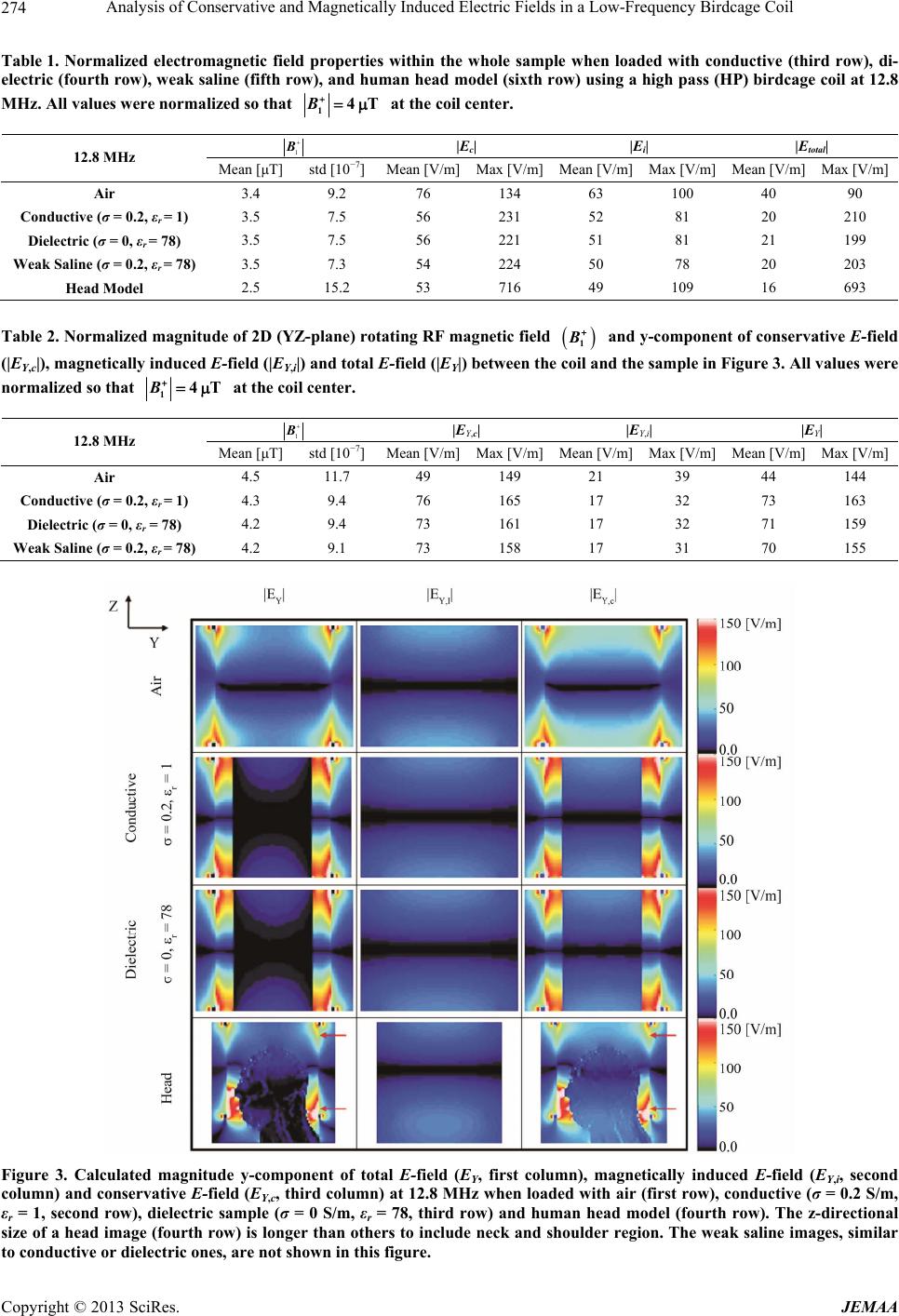

Analysis of Conservative and Magnetically Induced Electric Fields in a Low-Frequency Birdcage Coil 274
Table 1. Normalized electromagnetic field properties within the whole sample when loaded with conductive (third row), di-
electric (fourth row), weak saline (fifth row), and human head model (sixth row) using a high pass (HP) birdcage coil at 12.8
MHz. All values were normalized so that B14T
 at the coil center.
1

B
|Ec| |Ei| |Etotal|
12.8 MHz Mean [μT] std [10−7]Mean [V/m]Max [V/m]Mean [V/m]Max [V/m] Mean [V/m] Max [V/m]
Air 3.4 9.2 76 134 63 100 40 90
Conductive (σ = 0.2, εr = 1) 3.5 7.5 56 231 52 81 20 210
Dielectric (σ = 0, εr = 78) 3.5 7.5 56 221 51 81 21 199
Weak Saline (σ = 0.2, εr = 78) 3.5 7.3 54 224 50 78 20 203
Head Model 2.5 15.2 53 716 49 109 16 693
Table 2. Normalized magnitude of 2D (YZ-plane) rotating RF magnetic field


B1

and y-component of conservative E-field
(|EY,c|), magnetically induced E-field (|EY,i|) and total E-field (|EY|) between the coil and the sample in Figure 3. All values were
normalized so that B14T
 at the coil center.
1

B
|EY,c| |EY,i| |EY|
12.8 MHz Mean [μT] std [10−7]Mean [V/m]Max [V/m]Mean [V/m]Max [V/m] Mean [V/m] Max [V/m]
Air 4.5 11.7 49 149 21 39 44 144
Conductive (σ = 0.2, εr = 1) 4.3 9.4 76 165 17 32 73 163
Dielectric (σ = 0, εr = 78) 4.2 9.4 73 161 17 32 71 159
Weak Saline (σ = 0.2, εr = 78) 4.2 9.1 73 158 17 31 70 155
Figure 3. Calculated magnitude y-component of total E-field (EY, first column), magnetically induced E-field (EY,i, second
column) and conservative E-field (EY,c, third column) at 12.8 MHz when loaded with air (first row), conductive (σ = 0.2 S/m,
εr = 1, second row), dielectric sample (σ = 0 S/m, εr = 78, third row) and human head model (fourth row). The z-directional
size of a head image (fourth row) is longer than others to include neck and shoulder region. The weak saline images, similar
o conductive or dielectric ones, are not shown in this figure. t

Analysis of Conservative and Magnetically Induced Electric Fields in a Low-Frequency Birdcage Coil 275
loaded with the conductive, the dielectric phantom, and
the head model. The change of electric field near the end-
ring with and without the head model can be observed
(red arrows in the fourth row). The electric field distribu-
tion for the conductive sample, the dielectric sample, and
the weak saline (not shown) was very similar (see also
Table 3).
Figure 4 and Table 3 show the normalized z-compo-
Figure 4. Calculated magnitude of E-field z-component at 12.8 MHz. Other parameters are same as Figure 3. Note that the
magnitude of conservative E-field (EZ,c, third column) is increased when loaded with a conductive or a dielectric sample
whereas no difference in magnetically-induced E-field (EZ,i , second column). White rectangular dotted lines in a first column
indicate the region of a sample. The electric field distribution for the conductive sample, the dielectric sample, and the weak
saline (not shown) was almost the same.

Analysis of Conservative and Magnetically Induced Electric Fields in a Low-Frequency Birdcage Coil 276
Table 3. Normalized magnitude of 2D (YZ-plane) rotating RF magnetic field


B1

and z-component of conservative E-field
(EZ,c), magnetically induced E-field (EZ,i) and total E-field (EZ) within the sample in Figure 4. Other parameters are same as
Table 2.
1

B
|EZ,c| |EZ,i| |EZ|
12.8 MHz
Mean [μT] std [10−7]Mean [V/m]Max [V/m]Mean [V/m]Max [V/m] Mean [V/m] Max [V/m]
Air 3.3 9.0 29 67 29 67 4 31
Conductive (σ = 0.2, εr = 1) 3.4 7.3 32 105 29 67 10 83
Dielectric (σ = 0, εr = 78) 3.4 7.3 31 100 29 67 10 77
Weak Saline (σ = 0.2, εr = 78) 3.4 7.1 31 105 29 67 10 83
nent of c
E
, i
E
, and total E at 12.8 MHz along the
central sagittal plane (YZ-plane). The z-component of
c
E
within the sample was increased of about 10% in
average and 55% in maximum (Table 3) with addition of
a conductive sample, a dielectric sample or a weak saline
(not shown), whereas no changes were observed in the
z-component of i
E
.
Figure 5 shows the total magnitude of c
E
, i
E
, and
total and rotating RF magnetic field (1, fourth row)
after normalization for the coil empty (first column),
loaded with conductive cylinder (second column), di-
electric cylinder (third column) and human head model
(fourth column). For the coil loaded with conductive
sample, dielectric sample, and weak saline (not shown),
the
EB
c
E
and total Edecreased within the sample, but
increased in the space between sample and coil.
Figure 6 and Table 4 show the electromagnetic field
as a function of frequency (12.8 MHz, 64 MHz, and 128
MHz) for the empty coil (first row), and the coil loaded
with a weak-saline cylindrical sample (second row) and a
head model (third row). As frequency increased from
12.8 MHz to 128 MHz, the average magnitude of total
electric field within the weak saline sample (i.e., mean
||E||sample) increased of about 390% (i.e., 20 vs. 98 V/m ).
The fields for the coil loaded with a conductive or di-
electric sample (not shown) were similar to the ones of
the coil loaded with weak saline.
Figure 7 shows the calculated volume charge density
(



D
,where is the electric flux density) at the
frequencies of 12.8 (first column), 64 (second column),
and 128 MHz (third column) with different loading con-
ditions. The charge density was highly concentrated on
the surface of the sample or the head model regardless of
the operating frequencies.
D
4. Discussion
For the empty coil, the z-component of the i
E
—mainly
caused by the currents flowing along the rungs-is domi-
nant because i
E
is perpendicular to the magnetic flux
density following Faraday’s Law (Figure 2). On

B
the sagittal plane (YZ-plane) the x-component of i
E
mainly caused by the end-ring currents-was higher than
the y-component; the comparison was reversed on the
coronal planes.
The value of i
E
at the center was zero (Figures 2-5),
as expected given the specific electrical configuration of
the coil and can be explained by means of the magnetic
vector potential


A
, proportional to the current density


J
(Equation (3)). Because opposite sides of a bird-
cage coil in ideal mode 1 resonance have equal
J
flowing in the opposite direction and generating an op-
posing
A
, the two
A
having same amplitude and op-
posite direction cancel each other out at the center. In
these results, the value of electric field in the iso-center
of the coil was very close to zero but not exactly zero
(i.e., 0.04 V/m, less than 0.2% of average total electric
field within the whole sample). The c
E
was signifi-
cantly different when the coil was loaded with a conduc-
tive, a dielectric, a weak-saline sample, or a human head
model, with approximately a 25% - 30% change in the
average c
E
and up to 430% change in maximum
c
E
within the whole sample (Table 1). This was due
to the additional scalar potential (ϕ) within and sur-
rounding the sample, as shown in Figure 3. When a
conductive, dielectric, or weak-saline sample is located
within the electric field generated by the RF coil, charged
particles within the sample are moved to the boundaries
of the sample, resulting in a polarization field which ei-
ther has same or opposite direction of the original field
depending on the specific region considered and on the
components of the coil. Because of such polarization
effects, the z-component of c
E
(|EZ,c|) within the sample
increased (Figure 4 and Table 3); however, because the
additional scalar electric potential had opposite direction
of the original one, the y-component of c
E
(|EY,c|) de-
creased within the sample. Moreover, because |EY,c| was
the dominant component of the total , this resulted in an
overall reduction in the total and an increase of mag-
netic field homogeneity within the sample (Figure 3,
Tables 1 and 2). These results are in line with published
literature [8,9,11]. However, the |EY,c| between a coil and
E
E

Analysis of Conservative and Magnetically Induced Electric Fields in a Low-Frequency Birdcage Coil 277
Figure 5. Total magnitude of conservative E-field (Ec , first row), magnetically-induced E-field (Ei , second row), total E-field
(Etotal , third row) and rotating RF magnetic field (B1

, fourth row) after normalization when loaded with air (first column),
conductive sample (second column), dielectric sample (third column) and human head model (fourth column). The
z-directional size of a head image (fourth column) is longer than others to include neck and shoulder region. The electric field
distribution for the conductive sample, the dielectric sample, and the weak saline (not shown) was almost the same.
Table 4. Results of the 3D electromagnetic simulations within the sample at the different frequencies evaluated in this study.
Mean and standard deviation (std) of circularly polarized RF magnetic field


B1
 and total electric field (|E|) when loaded
with air, weak saline and human head model at three different frequencies of 12.8, 64, and 128 MHz.
1Sample

B
Mean [μT] std [10−7]
Mean |E|Sample [V/m]
Air (12.8 MHz) 3.4 9.2 40
Weak Saline (12.8 MHz) 3.5 7.3 20
Head (12.8 MHz) 2.5 15.2 16
Air (64 MHz) 3.6 6.9 159
Weak Saline (64 MHz) 2.9 7.1 85
Head (64 MHz) 2.3 14.4 75
Air (128 MHz) 3.6 6.4 315
Weak Saline (128 MHz) 1.5 8.4 98
Head (128 MHz) 1.9 12.7 119
a sample was increased because the additional scalar
electric potential-due to the presence of the sample-had
the same direction of the original one. This result extends
previous published literature showing that the total elec-
tric field would decrease within the sample when the coil
is loaded with a conductive or a dielectric sample (as
shown in (9,11)) (Table 1) and additionally demonstrate-
ing that the electric field increases between coil and the
sample (Table 2). This result may have consequences on
subject safety. For example, the accumulation of charge

Analysis of Conservative and Magnetically Induced Electric Fields in a Low-Frequency Birdcage Coil 278
Figure 6. Calculated total magnitude of E-field (|Etotal|) at three different frequencies of 12.8 (first column), 64 (second col-
umn), and 128 MHz (third column) for the empty coil (air—first row), and the coil loaded with a weak saline phantom (sec-
ond row) and a human head model (third row). The z-directional size of a head image (third row) is longer than others to
include neck and shoulder region.
on the boundary region of the sample may increase local
and 10 g-average SAR. Moreover, when external con-
ductive leads for physiological monitoring (e.g., ECG,
EEG) are present, the increase in electric field between
coil and sample may result in increasing induced currents
along the monitoring leads, with possible increase of
local SAR at the interface between leads and patient skin.
Because of difficulties of SAR and temperature calcula-
tion in free space, direct comparisons of losses and heat-
ing in the objects were not studied.
The electric field variation of the x-component with
addition of the samples was not shown in the figures be-
cause of the small absolute amplitude (less than 15%
compared to the y- and z-component for the sagittal view)
and because no difference was noticed among all the
loading samples considered. Additionally, the results
with a weak saline sample were similar to the results
obtained with a conductive or a dielectric sample (Tables
2 and 3).
The change for the magnetically induced E-field


i
E
with addition of the sample was much less when com-
pared to c
E
(i.e., about 13% - 18% change in the aver-
age i
E
and up to 22% change in the maximum i
E
)
(Table 1 and Figures 3-5). The reason that the value of
i
E
within and surrounding the sample appears to be
relatively independent of sample properties at 12.8 MHz
can be explained using Faraday’s law. i
E
is induced by
a time varying vector magnetic potential (Equation (2))
which is mainly caused by the conduction current flow-
ing in the RF coil. Because the RF coil used in this case
is very small (300 mm in length and 290 mm ID) com-
pared to the electrical wavelength (free space wavelength
at12.8 MHz equal to 23.4 m), the presence of the sample
does not significantly affect the distribution of coil cur-
rents (no wavelength effect) and specifically i
E
(Fig-
ure 5). However, as the frequency increased from 12.8
MHz to 128 MHz (free space wavelength equal to
2.34m), c
E
and i
E
both proportional to the frequency
(Equation (2)) also increased and the total was much
higher, (i.e., about 644% increase in average
E
total
E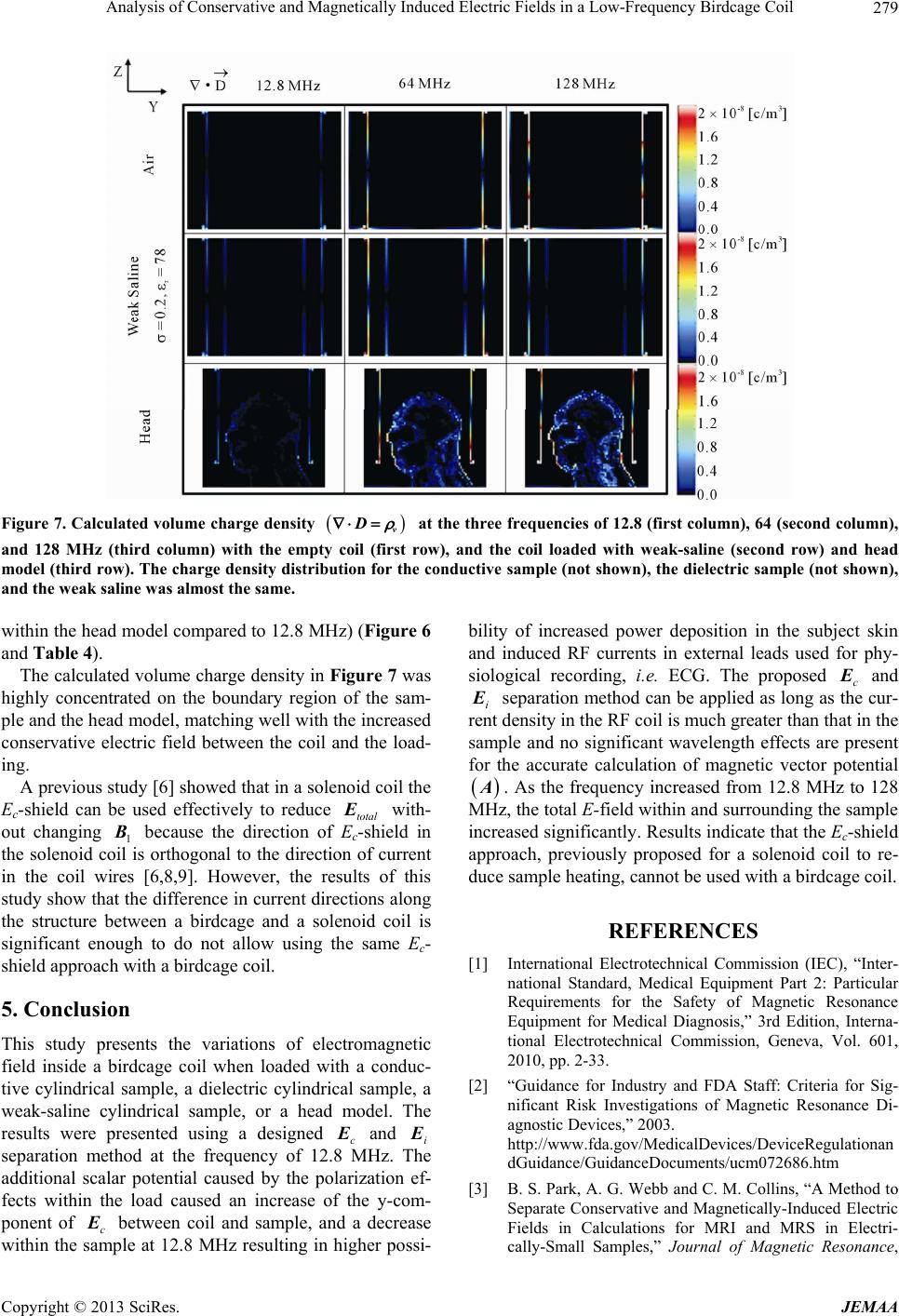

Analysis of Conservative and Magnetically Induced Electric Fields in a Low-Frequency Birdcage Coil 279
Figure 7. Calculated volume charge density

v
D


  at the three frequencies of 12.8 (first column), 64 (second column),
and 128 MHz (third column) with the empty coil (first row), and the coil loaded with weak-saline (second row) and head
model (third row). The charge density distribution for the conductive sample (not shown), the dielectric sample (not shown),
and the weak saline was almost the same.
within the head model compared to 12.8 MHz) (Figure 6
and Table 4).
The calculated volume charge density in Figure 7 was
highly concentrated on the boundary region of the sam-
ple and the head model, matching well with the increased
conservative electric field between the coil and the load-
ing.
A previous study [6] showed that in a solenoid coil the
Ec-shield can be used effectively to reduce total with-
out changing 1
E
B
because the direction of Ec-shield in
the solenoid coil is orthogonal to the direction of current
in the coil wires [6,8,9]. However, the results of this
study show that the difference in current directions along
the structure between a birdcage and a solenoid coil is
significant enough to do not allow using the same Ec-
shield approach with a birdcage coil.
5. Conclusion
This study presents the variations of electromagnetic
field inside a birdcage coil when loaded with a conduc-
tive cylindrical sample, a dielectric cylindrical sample, a
weak-saline cylindrical sample, or a head model. The
results were presented using a designed c
E
and i
E
separation method at the frequency of 12.8 MHz. The
additional scalar potential caused by the polarization ef-
fects within the load caused an increase of the y-com-
ponent of c
E
between coil and sample, and a decrease
within the sample at 12.8 MHz resulting in higher possi-
bility of increased power deposition in the subject skin
and induced RF currents in external leads used for phy-
siological recording, i.e. ECG. The proposed c
E
and
i
E
separation method can be applied as long as the cur-
rent density in the RF coil is much greater than that in the
sample and no significant wavelength effects are present
for the accurate calculation of magnetic vector potential


A
. As the frequency increased from 12.8 MHz to 128
MHz, the total E-field within and surrounding the sample
increased significantly. Results indicate that the Ec-shield
approach, previously proposed for a solenoid coil to re-
duce sample heating, cannot be used with a birdcage coil.
REFERENCES
[1] International Electrotechnical Commission (IEC), “Inter-
national Standard, Medical Equipment Part 2: Particular
Requirements for the Safety of Magnetic Resonance
Equipment for Medical Diagnosis,” 3rd Edition, Interna-
tional Electrotechnical Commission, Geneva, Vol. 601,
2010, pp. 2-33.
[2] “Guidance for Industry and FDA Staff: Criteria for Sig-
nificant Risk Investigations of Magnetic Resonance Di-
agnostic Devices,” 2003.
http://www.fda.gov/MedicalDevices/DeviceRegulationan
dGuidance/GuidanceDocuments/ucm072686.htm
[3] B. S. Park, A. G. Webb and C. M. Collins, “A Method to
Separate Conservative and Magnetically-Induced Electric
Fields in Calculations for MRI and MRS in Electri-
cally-Small Samples,” Journal of Magnetic Resonance,

Analysis of Conservative and Magnetically Induced Electric Fields in a Low-Frequency Birdcage Coil 280
Vol. 199, No. 2, 2009, pp. 233-237.
doi:10.1016/j.jmr.2009.05.007
[4] D. I. Hoult and P. C. Lauterbur, “The Sensitivity of the
Zeugmatographic Experiment Involving Human Sam-
ples,” Journal of Magnetic Resonance, Vol. 34, No. 2,
1979, pp. 425-433.
[5] W. Mao, B. A. Chronik, R. E. Feldman, M. B. Smith and
C. M. Collins, “Consideration of Magnetically-Induced
and Conservative Electric Fields within a Loaded Gradi-
ent Coil,” Magnetic Resonance in Medicine, Vol. 55, No.
6, 2006, pp. 1424-1432. doi:10.1002/mrm.20897
[6] B. S. Park, T. Neuberger, A. G. Webb, D. C. Bigler and C.
M. Collins, “Faraday Shields within a Solenoidal Coil to
Reduce Sample Heating: Numerical Comparison of De-
signs and Experimental Verification,” Journal of Mag-
netic Resonance, Vol. 202, No. 1, 2010, pp. 72-77.
doi:10.1016/j.jmr.2009.09.023
[7] D. G. Gadian and F. N. H. Robinson, “Radiofrequency
Losses on NMR Experiments on Electrically Conducting
Samples,” Journal of Magnetic Resonance, Vol. 34, No. 2,
1979, pp. 449-455.
[8] A. Krahn, U. Priller, L. Emsley and F. Engelke, “Reso-
nator with Reduced Sample Heating and Increased Ho-
mogeneity for Solid-State NMR,” Journal of Magnetic
Resonance, Vol. 191 No. 1, 2008, pp. 78-92.
doi:10.1016/j.jmr.2007.12.004
[9] F. D. Doty, J. Kulkarni, C. Turner, G. Entzminger and A.
Bielecki, “Using a Cross-Coil to Reduce RF Heating by
an Order of Magnitude in Triple-Resonance Multinuclear
MAS at High Fields,” Journal of Magnetic Resonance,
Vol. 128 No. 2, 2006, pp. 239-253.
doi:10.1016/j.jmr.2006.06.031
[10] P. T. Hardy Jr. and K. M. Weil, “A Review of Thermal
MR Injuries,” Radiologic Technology, Vol. 81, No. 6,
2010, pp. 606-609.
[11] Q. X. Yang, “A Method of Utilization of High Dielectric
Constant (HDC) Materials for Reducing SAR and En-
hancing SNR in MRI,” US Patent No. 20,110,152,670,
2011.
[12] K. R. Minard and R. A. Wind, “Solenoidal Microcoil
design-Part II: Optimizing Winding Parameters for
Maximum Signal-to-Noise Performance,” Nuclear Mag-
netic Resonance, Vol. 13 No. 3, 2001, pp. 190-210.
doi:10.1002/cmr.1008
[13] C. M. Collins and M. B. Smith, “Calculations of B1 Dis-
tribution, SNR and SAR for a Surface Coil Adjacent to an
Anatomically-Accurate Human Body Model,” Magnetic
Resonance in Medicine, Vol. 45, No. 4, 2001, pp. 692-
699. doi:10.1002/mrm.1092
[14] C. M. Collins and M. B. Smith, “Signal-to-Noise Ratio
and Absorbed Power as Functions of Main Magnetic
Field Strength, and Definition of ‘90˚’ RF Pulse for the
Head in the Birdcage Coil,” Magnetic Resonance in
Medicine, Vol. 45, No. 4, 2001, pp. 684-691.
doi:10.1002/mrm.1091
[15] K. Yee, “Numerical Solution of Initial Boundary Value
Problems Involving Maxwell’s Equations in Isotropic
media,” IEEE Transactions on Antennas and Propagation,
Vol. 14, No. 3, 1966, pp. 302-307.
doi:10.1109/TAP.1966.1138693
[16] C. Gabriel, T. Y. A. Chan and E. H. Grant, “Admittance
Models for Open Ended Coaxial Probes and Their Place
in Dielectric Spectroscopy,” Physics in Medicine and Bi-
ology, Vol. 39, No. 12, 1994, pp. 2183-2200.
doi:10.1088/0031-9155/39/12/004
[17] Federal Communication Commission (FCC), “Body Tis-
sue Dielectric Parameters,” 2010.
http://transition.fcc.gov/oet/rfsafety/dielectric.html