 Journal of Modern Physics, 2013, 4, 911-922 http://dx.doi.org/10.4236/jmp.2013.47123 Published Online July 2013 (http://www.scirp.org/journal/jmp) Macroscopic Violation of Duality Generated on a Laser Beam Daniel Mirell1, Stuart Mirell2 1Department of Chemistry, University of California at Irvine, Irvine, USA 2Department of Radiological Sciences, University of California at Los Angeles, Los Angeles, USA Email: smirell@ucla.edu Received April 20, 2013; revised May 25, 2013; accepted June 23, 2013 Copyright © 2013 Daniel Mirell, Stuart Mirell. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT It is shown theoretically and experimentally that passage of a laser beam through particular conventional Ronchi grat- ings prepares the beam in an altered state that violates quantum duality. The violation is characterized by a readily measured net transfer of energy between the prepared beam and an unmodified beam from a similar, independent laser. Notably, the experiment is conducted with the beams at macroscopic power levels where measurability of the dual- ity-violating transfer is vastly improved over that of the discrete photon regime. These results are consistent with other recently reported experiments that have challenged the validity of the duality-related principle of complementarity. Keywords: Quantum Duality; Local Realism; Probabilistic Interpretation 1. Introduction Wave-particle duality is a central principle of the standard probabilistic interpretation of quantum mechanics. We report the results of an experiment violating that principle. The experiment demonstrates a net power transfer be- tween a specially prepared state of a continuous-wave (cw) laser beam ΦG and an ordinary beam ΦR at the same wavelength but generated by an independent laser where both beams are at macroscopic power levels. The net transfer is established by first intersecting ΦG and ΦR over a common coupling path and measuring beam power on a sample region of the ΦG beam spot separated from ΦR at the terminus of that path. ΦR is then blocked from the coupling path and beam power of ΦG in the same sample region is re-measured to provide a baseline power for the calculation of the net power transfer. ΦG is prepared in three different states, “depleted”, “enriched”, and “ordinary”, in order to provide for three distinct experimental trials. The total beam power of ΦG is substantially identical for these states. The results of these trials show that when ΦG is prepared in a depleted state, coupling to ΦR results in a net transfer of power to ΦG. Alternatively, when ΦG is prepared in an enriched state, a net transfer of power out of ΦG occurs when coupled to ΦR. Lastly, ΦG is prepared in an ordinary state which is shown to yield no net transfer upon coupling with ΦR. From the perspective of the probabilistic interpretation, independently generated ΦG and ΦR will still demonstrate interference along an intersection region of those beams, despite Dirac’s dictum that a photon can interfere only with itself [1], based upon a theoretical analysis by Mandel [2]. However, the probabilistic interpretation provides no mechanism by which the observed net trans- fer would occur when ΦG is in a presumptive altered state of depletion or enrichment. Specifically, we show here that the source of the duality violation originates with the preparation of ΦG in these presumptive altered states. As an alternative, a theoretical construct derived di- rectly from principles consistent with local realism phy- sically represents these altered states and quantitatively predicts the respective transfers reported here. 2. Background The probabilistic interpretation of quantum mechanics is distinguishable from local realism by the self-interaction of discrete photons incident on mechanisms such as a beam splitter or a double slit. For local realism, the pro- babilistic property of duality in the discrete photon re- gime is violated by the wave packet that emerges from one of the two outputs of such mechanisms as an “empty” wave. That empty wave is forbidden by duality which requires an inseparability of a photon’s wave-like prop- erty, probability, and its particle-like property, the energy quantum. Duality effectively imposes a fixed proportion- C opyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL 912 ality between those two properties. In local realism, the treatment of wave-like and particle-like properties as manifestations of two separate and real entities has its origins in de Broglie’s initial reality-based pilot wave re- presentation of quanta phenomena [3]. Empty waves, if they exist, should in principle yield testable consequences for a variety of phenomena com- monly associated with the wave-like properties of pho- tons. Important advances in the study of these phenom- ena have been made by a number of investigators in- cluding Croca, Garuccio, Lepore, Moreira, Selleri, and others e.g. [4-7]. Popper, in seeking a rational hypothesis for empty waves, has raised compelling philosophical arguments that question the validity of the prevailing probabilistic interpretation [8]. Testability for empty waves in the context of double slit experiments is related to determining which slit is traversed by an energy-bearing photon without destroy- ing accompanying interference arising from both slits, a result consistent with an empty wave traversing the other slit but in conflict with Bohr’s duality-related principle of complementarity [9]. Recently, two notable investiga- tions [10] and [11] employing different methodologies have experimentally realized slit traversal determination with verified accompanying interference. The methodology of one investigation has its origins in an analysis by Aharonov et al. [12] showing that a “weak” measurement of a system can provide some de- gree of information about the system without signifi- cantly altering its subsequent interactions thereby pro- viding an effective investigative tool [13-16]. Wiseman’s assessment that such weak measurements could be used to establish average trajectories [17] is experimentally demonstrated in the recent investigation by Kocsis et al. where averaged slit-specific trajectories are measured from a double slit accompanied by interference in the far field of the slits [10]. In a different approach, Rabinowitz proposes a novel double slit experiment using correlated photon pairs in which the passage of discrete photons through a particu- lar slit can be definitively established together with an observation of interference in the far field beyond the slits [18,19]. A recent investigation by Menzel et al. re- ports the results of an analogous correlated photon pair experiment in which the slit traversed by a discrete pho- ton is determined and far-field interference arising from both slits is verified [11]. The investigations referenced above in this section are inherently associated with the microscopic regime of discrete quantum entities. In this regard it is significant that local realism imposes no constraints on duality vio- lation in the discrete quantum regime as well as in the cw regime where a parameter such as beam power can be at a macroscopic level. Probability in local realism is a relative entity associ- ated with a real wave structure and retains its original restricted interpretation in Born’s rule [20] as the likeli- hood or “propensity” [8] of a particle-like energy quan- tum progressing onto a particular probability channel in a complete set of out-going probability channels. A re- scaling of the total probability distributed to the complete set does not alter the likelihood of the particle-like entity entering onto that particular channel. We continue to use the term “probability” here bearing in mind that its usage is potentially misleading since that term suggests equi- valence to a mathematical absolute probability. That equi- valence is manifested in the probabilistic interpretation as the principle of duality. In the macroscopic cw regime the treatment of prob- ability as a relative quantity implies that for any number of resident energy quanta on some arbitrary beam seg- ment there is not an imposed, fixed proportionate value of inclusive probability. Consequently, a mechanism predicted by local realism to generate even a modest (du- ality-violating) disproportion on a cw beam of macro- scopic power contributes to conclusive experimental test- ability. This advantage arises because the net “excess” or “deficit” of particle-like energy quanta residing on the probability’s wave-like structure would provide a readily measurable macroscopic power increment. Clearly, a beam splitter does not provide local realism with the requisite mechanism to achieve duality violation in the macroscopic cw regime. In the transition from the discrete to the macroscopic regimes as beam power is increased, statistical distribution of the numerous inci- dent energy quanta onto the beam splitter’s two output channels restores a proportionality of probability and energy quanta on both of those channels that is not dis- tinguishable from that of duality. However, there are a number of mechanisms consistent with local realism, e.g. [21], that generate duality violation at macroscopic pow- er levels. We report here on one of those mechanisms, its theoretical basis, and on the experimental demonstration of duality violation using that mechanism. 3. Mechanism for Duality Violation The basic mechanism for duality violation presented here can most readily be appreciated by first considering a simple gedanken experiment before proceeding to the particular realization of that experiment reported here. In the gedanken experiment we use a Ronchi transmission grating (ruling) and a laser beam at normal incidence. A Ronchi grating consists of a linear array of equal-width opaque and transmissive bands resulting in a grating pe- riod 2pw where w is the “slit” width represented by the transmissive bands. In the gedanken experiment, we hold the laser beam wavelength constant at some λ and consider the consequences of progressively decreasing w Copyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL 913 from large values of w 2pw down to small values of w ~ λ while maintaining . The irradiated slits produce the Figure 1 “output” set of wavelets that do not intersect in the grating’s near field. The total output probability emerging on these wavelets is a constant Po independent of w since the transmissive factor for a Ronchi is 0.5 wp. In arbi- trary units, we can set Po = 1. As the individual wavelets expand in the grating’s far field, they generate smoothly- varying single-slit envelopes that intersect and interfere thereby producing the “resultant” set of highly direc- tional diffraction orders j shown in Figure 2 for the Fraunhofer approximation. The envelope intensity is proportional to 22 2 sin csin where πsinw and θ is the physical azimuthal angle. The depicted envelope in Figure 2 is equivalent to an individual slit envelope scaled up by the total number of irradiated slits to correctly show the essential equivalence of the output integral and the integral over the resultant peaks. For Ronchi gratings, the side lobes are bisected by the symmetrically disposed odd ±j orders for |j| and the integral over a particular side lobe is equal to the integral of the odd jth resultant peak bisecting that side lobe. Fig- ure 2 is parameterized in terms of the continuous vari- Figure 1. Emergent output diffraction wavelets from irra- diated individual slits fully determine collective output pro- bability (and energy) prior to the formation of resultant orders by interference as those wavelets intersect. Figure 2. Single slit output diffraction intensity envelope and associated resultant diffraction intensity peaks for a Ronchi grating of those slits. The single slit envelope is scaled up by number of irradiated slits N = 20 to correctly depict total envelope output intensity relative to that of the resultant peaks. The depicted total envelope output and the resultant peaks are both scaled up by ×15 in the detail graph of the j = 2 to 6 range. able 2πj as well as α since j conveniently as- sumes integer values at the side lobe bisector points and null points. Before proceeding further, we introduce a convention useful in the present theoretical analysis. Beam probabil- ity P is evaluated by volumetric integration of intensity over a beam segment of some arbitrary selected length. Correspondingly, this defines an inclusive energy E on that beam segment. We use the convention of considering beam segments purely as a convenience in order to pro- ceed with the theoretical analysis using the parameters of probability and energy rather than the associated flux densities of those parameters. Nevertheless, the results of the analysis are fully applicable to the experimentally relevant parameter of the integrated energy flux density, i.e. power, which is proportionate to that inclusive energy E. From a straight-forward classical calculation [22], the resultant probability of the diffraction orders 2 π2 2 π2 πsin 2 sin d tt tt n j jn rt j F j c Pj c (1) is given by the integral over the resultant order intensities, expressed here as a Riemann sum, divided by the integral of the output envelope intensity. The output envelope truncates at πw t 90 where the azimuthal . Truncation on the j continuum is given by F ttrt is shown as a function of the con- venient parameter jt, but that functional dependence is fundamentally the linearly related parameter 2π.jPj .Pj F trt is subscripted by F to indicate that the quantity is valid in the Fraunhofer approximation. Because of symmetry, dependence on jt is equivalent to that for –jt. From these expressions, we have a useful relationship for the Ronchi slit width in terms of jt, 2. t wj (2) The Riemann sum truncates at the ±nth final resultant orders inclusive within ±αt. Those ±nth orders are respec- tively in the neighborhood of and are said to be near the grating “threshold”. 90 In particular, the total output probability Po was shown The basis for the derivation of Equation (1) [22] can be succinctly summarized here. An integral over resul- tant order intensities (or its Riemann sum equivalent) would normally by itself constitute the requisite resultant probability unlike the form of Equation (1). However, in the present case the integral over resultant orders as well as the output envelope integral are both computed over α and not the physical azimuthal angle θ causing both inte- grals to exhibit an artifactual decrease as the variables αt, jt, and w in our gedanken experiment mutually decrease. Copyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL 914 above to physically remain constant independent of w. Accordingly, the divergence from constancy of the out- put integral evaluated over α yields the requisite nor- malization factor for the corresponding resultant order integral over α to provide a probability Pr for which the α-related artifactual decrease is selectively eliminated. Turning now to the beginning of our gedanken ex- pe some riment in the limit of large w, which corresponds to “coarse” gratings, the significant central region of the output envelope and all of the correspondingly signifi- cant resultant diffraction orders are tightly clustered in the forward direction about 0˚ and, equivalently, about α = 0 consistent with the Fraunhofer approximation. The more distal envelope and higher orders extending out to 90 are vanishingly small where both “truncate” at large |j|. In this limit the Equation (1) F rt Pj is very nearly a constant value of unity. This con for large w merely expresses the high degree to which prob- ability is conserved for a coarse grating in the transition that occurs as the expanding wavelets interfere and gen- erate in their place the highly directional resultant orders. However, as w stancy for “fine” gratings, only the en- v maxim F he resu elope’s central um and significant proximal side lobes are included over the –90˚ to +90˚ full azimuthal span as truncation occurs at some small |j|. Correspond- ingly, that same truncation also leaves only a very few orders, including those with the most significant intensi- ties, widely dispersed over –90˚ to +90˚. This departure from the Fraunhofer approximation necessitates that we amend the Equation (1) rt Pj to properly represent the relative intensities of tltant orders as a func- tion of inclination from 0˚ by incorporating the classi- cally well-known “obliquity” correction appropriate for the presently considered Ronchi grating diffraction sys- tem. The relative actual intensities of orders nearer threshold are reduced below that predicted by the 2 sin c function. A physically accurate obliquity cor- n the present experiment is readily available em- pirically from a direct measurement of the beam powers of the resultant jth orders emerging from an appropriate fine grating and comparing those powers to the 2 sin rection i c function. Our primary interest in this investig confined to gratings for which jt ranges from ±4 down to ±2 respectively over the first side lobes. For a Ronchi grating the probabilities (integrated intensities) of those output side lobes are expressed in turn by the probabili- ties associated with the bifurcating resultant ±3rd orders. Accordingly, we measure the powers of the resultant orders with a Ronchi grating that places the ±3rd orders near threshold. From these measurements, we obtain an obliquity correction of f = 0.56 for those ±3rd orders near threshold and a correction negligibly differing from unity for the lower orders within the diffraction envelope’s central maximum. Similarly, that obliquity correction f is also applicable to the output integral over the first side lobe. The ation is obliquity-amended expression for the Equation (1) resultant probability rt Pj 22 01 π2 π 22 0π 2 33 π2 π 22 0π 3 π2 2 π 0.5π0.5sin sin sin dsin d 0.5πsin sin dsin d 2.539 0.071 2.532sin d t t t jj j j j j cc cf c fS c cfc S c (3) is valid when the truncation j resides in the first side lobe t 24 t j . Because of symmetry about 0 on the jt con- ative j terms have been excluded in the Rie- mann sum. Since the negative αt limits in the envelope integration have also been excluded, Equation (3) still represents the total resultant probability for all positive and negative orders within . t j tinuum, neg S3 is a step function, zero when the j = 3 order is excl and unity when the j = 3 order is included in the integrated output envelope. uded rt Pj exhibits a discontinuous perturbation about unity t. This perturbation is also present for the other odd 3 t j, but these perturbations rapidly diminish with sing jt as depicted in Figure 3. In this figure, the obliquity correction is applied to the second side lobes as well as the first side lobes in order to depict the diminution of the perturbation at jt = 5 relative to that at jt = 3. The perturbations are not true mathematical discontinuities but approach that status as the number of irradiated slits be- comes large. The origin of t at j = 3 increa hese perturbations is understood from Equation (3). Interference of the Figure 1 wavelets con- verts the output probability into resultant probabilities represented by the highly directional diffraction orders. As w → λ, truncation leaves only a very few orders prop- agating over −90˚ to +90˚. Consider for example the be- Figure 3. Total resultant probability Pr(jt) inclusive of all valid. diffraction order probabilities within the truncation limits ±jt. For large jt, the total resultant probability Pr(jt)F = 1 is Copyright © 2013 SciRes. JMP 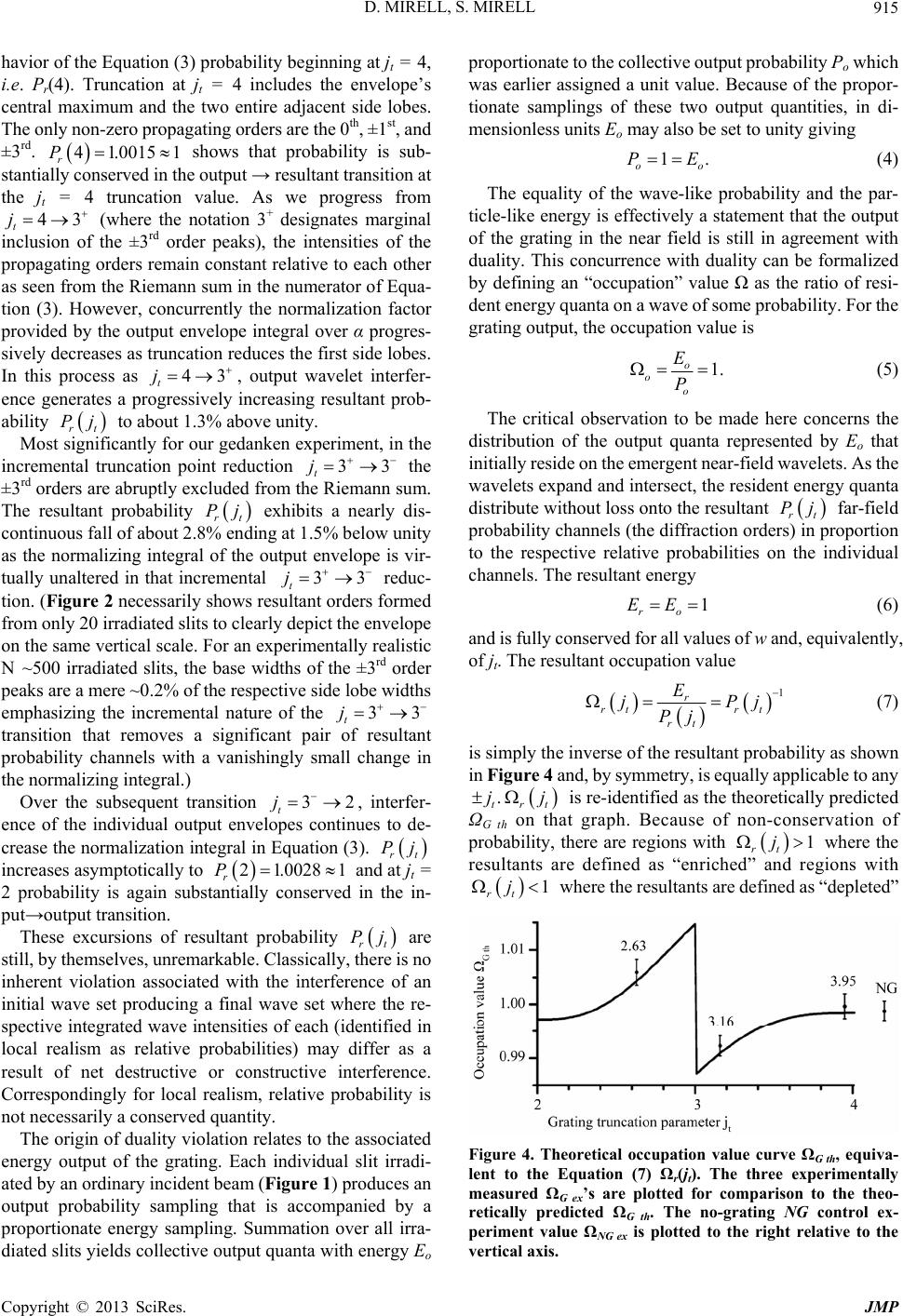 D. MIRELL, S. MIRELL 915 havior of the Equation (3) probability beginning at jt = 4, i.e. P(4 r). Truncation at jt = 4 includes the envelope’s central maximum and the two entire adjacent side lobes. The only non-zero propagating orders are the 0th, ±1st, and ±3rd. 41.0015 1 r P shows that probability is sub- stantially conserved in the output → resultant transition at the jt = 4 truncation value. As we progress from 43 t j (where the notation 3+ designates marginal inclusion of the ±3rd order peaks), the intensities of the propagating orders remain constant relative to each other as seen from the Riemann sum in the numerator of Equa- tion (3). However, concurrently the normalization factor provided by the output envelope integral over α progres- sively decreases as truncation reduces the first side lobes. In this process as 43 t j , output wavelet interfer- ence generates a progressively increasing resultant prob- ability rt Pj to about 1.3% above unity. Most significantly for our gedanken experiment, in the incremenuncation point reduction j tal tr33 t the ±3rd orders are abruptly excluded from the Riemann sum. The resultant probability rt Pj exhibits a nearly dis- continuous fall of about 2.8% ending at 1.5% below unity as the normalizing integral of the output envelope is vir- tually unaltered in that incremental 33 t j reduc- tion. (Figure 2 necessarily shows resultant orders formed from only 20 irradiated slits to clearly depict the envelope on the same vertical scale. For an experimentally realistic N ~500 irradiated slits, the base widths of the ±3rd order peaks are a mere ~0.2% of the respective side lobe widths emphasizing the incremental nature of the 33 t j transition that removes a significant pair of resultant probability channels with a vanishingly small change in the normalizing integral.) Over the subsequent transition 32 t j , interfer- ence of the individual output envelopes continues to de- crease the normalization integral in Equation (3). rt Pj increases asymptotically to 21.00281 r P and at jt = 2 probability is again substantially conserved in the in- put→output transition. These excursions of resultant probability rt Pj are still, by themselves, unremarkable. Classically, th inherent violation associated with the interference of an initial wave set producing a final wave set where the re- spective integrated wave intensities of each (identified in local realism as relative probabilities) may differ as a result of net destructive or constructive interference. Correspondingly for local realism, relative probability is not necessarily a conserved quantity. The origin of duality violation relates to the associated energy output of the grating. Each in ere is no dividual slit irradi- ated by an ordinary incident beam (Figure 1) produces an output probability sampling that is accompanied by a proportionate energy sampling. Summation over all irra- diated slits yields collective output quanta with energy Eo proportionate to the collective output probability Po which was earlier assigned a unit value. Because of the propor- tionate samplings of these two output quantities, in di- mensionless units Eo may also be set to unity giving 1. oo PE (4) The equality of the wave-like ticle-like energy is effectively a of probability and the par- statement that the output the grating in the near field is still in agreement with duality. This concurrence with duality can be formalized by defining an “occupation” value Ω as the ratio of resi- dent energy quanta on a wave of some probability. For the grating output, the occupation value is 1. o o E P o (5) The critical observation to be m distribution of the output quanta represented by Eo that in n the ade here concerns the itially reside on the emergent near-field wavelets. As the wavelets expand and intersect, the resident energy quanta distribute without loss onto the resultant rt Pj far-field probability channels (the diffraction orders) in proportion to the respective relative probabilities oindividual channels. The resultant energy 1 ro EE (6) and is fully conserved for all val of jt. The resultant occupation va ues of w and, equivalently, lue 1 r rt r E jP Pj t rt j (7) is simply the inverse of the resultant proba in Figure 4 and, by symmetry, is equally applicable to any bility as shown . trt jj is re-identified as the theoretically predicted ΩG th on that graph. Because of non-conservation of there are regions with 1 rt j where the resultants are defined as “enriched” and regions with probability, 1 rt j where the resultants are “depleted” defined as Figure 4. Theoretical occupation value curve ΩG th, equiva- lent to the Equation (7) Ωr(jt). The three experimentally is. measured ΩG ex’s are plotted for comparison to the theo- retically predicted ΩG th. The no-grating NG control ex- periment value ΩNG ex is plotted to the right relative to the vertical ax Copyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL 916 in reference to the respective disproportionalities of resi- dent energy quanta relative to probability. Resultant beams with Ω = 1 are defined as “ordinary”, a designation that also applies to the incident beam and the grating output. In the realization of our gedanken ex- periment, we use particular Ronchi gratings with w values that are predicted to respectively generate enriched and depleted resultant beams. Any individual jth order of the resultant orders has the same occupation value as that of the entire set, i.e. rj r , because occupation values are intrinsic variables formed from quotients of the ex- trinsic variables of energy and probability. A particular jth order beam with a probability Prj acquires a rjr PP share of the total energy or EE as it leaves the near-field of the grating. Before proceeding with the performed experiment, we note that the discontinncountered in a transition such as uity e t presumptively duality- vi probabilistic interpretation. H ular grating where a prepared beam ΦG may spe- ci - that from the depleted region to the enriched region when 33 t j is characterized by the energy quanta that had been on the ±3rd orders being redistributed onto the remaining propagating orders. This abrupt redistribu- tion of energy onto remaining orders as an order passes threshold is superficially analogous to a “Rayleigh grating anomaly”. Historically, the incident beam used to study grating anomalies is multi-wavelength where the beam energy (or power) is at most a slowly varying function of wavelength. Rayleigh anomalies relate to those photons at some particular wavelength λt that have an order “at threshold” i.e. at the grating plane. In Rayleigh’s analysis [23], the photons on that threshold order are coherently scattered off of deep grating grooves (relative to λt) and are redistributed onto the remaining propagating orders of the λt photons. As a result, those remaining orders of the λt photons exhibit an abrupt increase in energy relative to the energy on the corresponding orders of marginally shorter wavelength λnt photons that have an unscattered order near threshold (denoted by “nt”) but not at threshold. Significantly, the scattered λt photons carry not only the energy quanta but also the associated wave packet onto the remaining propagating orders. Consequently, the Rayleigh anomaly is consistent with probabilistic duality (as well as with local realism). In this context, we note that the Ronchi gratings used in this experiment have thin opaque bands relative to wavelength (see Figure 1 where “t” refers to thickness), and would not be expected to provide the photon scattering mechanism associated with gratings actually demonstrating the Rayleigh anomaly. Clearly, a methodology to directly measure the duality state of the Ronchi grating propagating orders must be utilized in order to establish whether those orders are ordinary, as would be expected for Rayleigh anomalies, or are in fact “duality-modulated” (Ω deviations from unity) as predicted by local realism. The experiment presented in the next section to provide that direct test for duality modulation utilizes a transient coupling between a resultan olating beam from the grating (a propagating order) and an independent ordinary beam [22]. The coupling setup is analogous to the intersection of two independent beams used in numerous investigations to experimentally assess duality violation by determining the presence or absence of interference between the intersected beams as a test of the probabilistic interpretation. An excellent review of these investigations is given by Paul [24]. An observa- tion of interference would seemingly violate Dirac’s dic- tum that a photon in the probabilistic interpretation can interfere only with itself [1]. The outcomes of these numerous investigations are conclusive demonstrations that interference does occur in apparent contradiction to the owever, in a theoretical analysis of this phenomenon, Mandel makes the critical argument that for any given photon measured in the interference we do not know on which beam that photon had initially resided [2]. Because of that lack of knowledge, each photon is treated in Mandel’s analysis as interfering with itself. Consequently, interference in the intersection of independent beams is widely regarded as consistent with the probabilistic in- terpretation and as not providing a test of that interpreta- tion. In a variant of those independent beam investigations, we prepare one of the beams by transmission through a partic fically violate probabilistic duality, i.e. the beam is in a depleted or enriched state from the perspective of local realism. Spatially transient coupling of that prepared beam with an independent ordinary “restoration” beam ΦR by mutual interference over a coupling path should then yield a net equilibrating transfer of energy quanta for local realism but not for the probabilistic interpretation. That net energy transfer relative to ΦG is experimentally readily measurable in the cw regime at macroscopic powers by detecting the beam power on a sampling of ΦG that is substantially separate from ΦR at the end of the coupling path with and without ΦR present on the coupling path. 4. Experimental Configuration and Methods We begin with a description of the experimental con figuration shown in Figure 5. A HeNe laser generates a horizontally linearly polarized beam Φ of several milli- watts at 633 nm. Beam Φ traverses a variable attenuator AttG and an optical beam chopper wheel Ch with a 0.5 duty cycle generating square wave pulses at 40 Hz. Φ is at normal incidence on a grating G. The grating is one of three Ronchi gratings (rulings) with respective slit widths w = 833 nm, 1000 nm, and 1250 nm formed from opaque bands of 150 nm-thick reflective chromium deposited on a Copyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL 917 Figure 6. Detail of Figure 5 coupling path, not to scale, showing the substantial separation of ΦR from ΦG at the detector det by convergence of the former onto a disk mas t of duality violation with this Figure 5 onfiguration imposes some essential general criteria on us parameters in the region de At BS the diameter of aque disk mask beam st general identifiers of the respective beams, but w Figure 5. Experimental apparatus configuration showing a potentially duality-modulated beam ΦG after passage through a particular grating G. ΦG is equilibrated with an ordinary are 600, 500, and 400. The slit widths uniquely haracterize each grating through Equation (2) which it widths. Accordingly, the in- dividual gratings are also uniquely chara Equation (8) j-continuum truncation point beam ΦR along a coupling path extending from beam splitter BS. Coupling occurs with beam blocker BR shifted to trans- mit ΦR. glass substrate. The respective grating frequencies in lines/mm c gives the w-dependent j-continuum truncation points in terms of the slits’ widths where λ = 633 nm in this invest- tigation. These points are 2.63,3.16,and 3.95 t jw (8) for the three respective sl cterized by the s. In our nota- tion a Ronchi grating of some arbitrary slit width w is denoted as t Gj or simply G. Conversely, a grating identified with a numerical t jw -equivalent truncation point identifies a particular grating with an implicitly expressed slih as in G(2.63), G(3.16), and G(3.95) for the three selected gratings use of jt continues our convention in which variables are most instructively identified by the critical j-continuum truncation value. The motivations for selecting these three gratings are their duality properties based on Equation (7). G(2.63), G(3.16), and G(3.95) are respectively predicted to pr t widt . This o- du ic) TM (S) polari- za ce enriched, depleted, and ordinary resultants. Data are also acquired with no grating present. These trials, which are designated by NG, should produce ordinary resultants and serve as control experiments. The particular grating under study is mounted with the grating bands on the exit face and vertically oriented thereby providing (transverse magnet tion with respect to G in the usual classical configura- tion for observing grating anomalies. The 0th order dif- fraction beam identified as ΦG is incident on a 50:50 me- tallic plate beam splitter BS with a 3 mm thick glass sub- strate and the metallic deposition on the exit face. An independent HeNe laser generates a horizontally linearly polarized beam ΦR initially several milliwatts in power. ΦR traverses a variable attenuator AttR, a retractable beam blocker BR and enters a beam expander, L1 (f = +100 mm) and L2 (f = +200 mm), before forming a beam spot con- centric with that of ΦG on the beam splitter BS as shown in the Figure 6 detail view. This concentricity is a critical k beam stop Bm. alignment for the apparatus. Measuremen c the set of beam and apparat signated as the “coupling path” that extends from BS to the final optical components. We include those general criteria below, augmented by specific examples of pa- rameter values given in parentheses that are taken from an experimentally utilized parameter set. In that set, specified beam widths are Gaussian diameters. The equivalency of the ΦG and ΦR polarization angles should be verified on the coupling path itself and cor- rected by rotation of ΦR if necessary. ΦR (1.8 mm) is expanded slightly beyond that of ΦG (1.7 mm) as a result of the L1 and L2 relative spacing. The beam components exiting BS utilized here are the trans- mitted component of ΦG and the reflected component of ΦR. The orientation of BS is adjusted to concentrically align the ΦR beam spot to the ΦG beam spot at the terminus of the coupling path. This critical, second beam spot alignment coaxially aligns the ΦR and ΦG beams over the coupling path length (~2000 mm). An assembly of a beam blocker Bm, an iris diaphragm Ir, and a photodiode detector Det is located at the coupling path terminus. Bm consists of an op op (diameter 1.7 mm) mounted on a glass substrate as detailed in Figure 6. At Bm, natural divergence from the source laser has further increased the diameter of ΦG (3.8 mm) to a value significantly larger than that of the Bm disk mask. Conversely, the relative spacing of L1 and L2 is critically adjusted to converge the ΦR diameter (1.0 mm) to a value significantly less than that of the Bm beam mask. The iris (3.3 mm dia.) is set to exclude the peripheral portion of ΦG from the detector Det. Beam directors on the coupling path (not shown in Figures 5 and 6) are used to provide concentric alignment of ΦG and ΦR with Bm, Ir, and Det. Data are acquired with one of the three Ronchi gratings in the Figure 5 position of G. We continue the use of ΦG and ΦR as e are reminded that these wave functions in local realism are exclusive of the energy quanta residing on those beams. Copyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL 918 Consistent with our prior notation, the complete ex- pression for occupancy of that ΦG beam would formally be identified as j since jt designates the unique tr ifies its G g is tha the wave struc- tu e end of the coupling path. We use the added ables such as Ω to denote values a is criterion is satisfactorily ap- pr 0rt ncation point on the j-continuum for any Ronchi grat- ing t GGj, r denotes that ΦG is a resultant diffraction beam and 0 specorder. These identifiers are al- ready understood in the present context and the compact expr is used here in place of 0rt j. Similarly, an ΩR = 1 designates the occupation value of the initially ordinary restoration beam ΦR. The basic premise of beam couplint a duality modulated beam equilibrates with an ordinary beam by a net transfer of energy quanta that leaves u ession Ω res of both beams unchanged and ideally converges the occupation values toward a common value. For the ob- jective of achieving complete equilibration, Gc Rc (9) as the two beams ΦG and ΦR approach th subscript “c” on vari- t the end of the coupling path where equilibration of ΦG and ΦR has potentially altered those values (in contrast to the respective values of those variables without ΦG and ΦR simultaneously present on the coupling path). ΦR should ideally serve as an infinite source for a de- pleted ΦG or an infinite sink for an enriched ΦG in the equilibration process. Th oximated when the inequality G PP (10) is satisfied by a ratio of ~100:1 leaving the final equili- brated ΦG and ΦR both as or Equation (9) Ω equality to a un - ing G, a net transfer of energy ΔE w and ΦR that changes the initial grat EG ng path terminus is approached. A positive- signed ΔE corresponds to an energy transfer from ΦR where ΦG had ini ling path terminus for our choice of arbitrary units. A sampling of this EGc is acquired by the detector. Ideally, the wave-like prob dinary and extending the it-valued ordinary value, 1. Gc Rc (11) If ΦG is depleted or enriched as it emerges from a grat ill occur between ΦG ing-emergent energy of ΦG to Gc G EE E (12) as the coupli gained by ΦG in a tially been depleted. Similarly, if ΦG had initially been enriched, ΔE is nega- tively signed. Alternatively, if ΦG emerging from G is initially ordinary, no net transfer occurs and ΔE is zero. The coupling equilibration of ΦG to an ordinary state (if it is not already in an ordinary state) provides the impor- tant result GGc PE (13) at the coup ability PR is entirely con- fined to the mask of Bm as PRm = PR and the residual probability of PR in the detector’s annular sampling region PRa = 0, but this extreme criterion is impractical for the Figure 5 apparatus. However, this criterion can be satis- factorily approximated by . mRa PP (14) The criteria given by the inequalities of Equations (10) and (14) are expressed in terms of probabilities which are not directly amenable to measu th rement. Nevertheless, for e modest deviations of Ω from unity on the order of one percent realized in the present experiment, the two ine- qualities are equivalently representable in terms of the corresponding energies ER, EG, ERm, and ERa. These ener- gies, in turn, are proportional to the experimentally measurable corresponding beam powers PWRR (~600 μW), PWRG (~6 μW), PWRRm (~600 μW), and PWRRa (~2.5 μW) which can be substituted for the probabilities in the two inequalities for the purposes of setting up the apparatus. Correspondingly, the ΦG pulse height is measured from the power PWRGa (~2.5 μW) incident on the detector. (With the chopper wheel in rotation, the detector amplifier registers an average power of PWRGa/2 for the pulsed ΦG). The beam power objectives on the coupling path are achieved by adjustment of the variable attenuators AttG and AttR. For data acquisition in the experiment with a particular t GGj in place, the output voltage of the detector amplifier provides a proportionate instantaneous measure of the energy incident on the detector in the annular sam- g rgin. With the chopper wheel in rotation, the de- tector amplifier signal received by a digital oscilloscope produces a square wave of a height proportional to the pulsed ΦG energy. A trapezoidal-like deviation from a true square wave is caused by partial eclipsing of the ΦG beam by the vanes of the chopper wheel. That deviation, which represents in- co pline o mplete detection sampling of ΦG, is reduced to an in- significant level relative to the complete sampling when the ratio of the Gaussian diameter of ΦG to the arc span between adjacent vanes is very small (~1:100 in the pre- sent apparatus). This reduction is most readily achieved when using a chopper wheel with a minimal number of vanes. With the oscilloscope set to dc coupling of the signal input, the ΦG square wave rides on the baseline bias level produced by any steady state flux of photons in the an- nular sampling region. When ΦR is blocked from the coupling path, that flux consists only of background pho- tons. When ΦR is unblocked, that steady state flux addi- tionally includes ΦR photons residually in the annular sampling region and accordingly significantly elevates the baseline bias level. Conversely, with the oscilloscope set Copyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL 919 to ac coupling of the signal input, the ΦG square wave appears as alternating positive and negative half-height square pulses symmetrically distributed about the hori- zontal zero voltage midline independent of a blocked or unblocked ΦR. For either mode of signal coupling, in- cremental changes in the full pulse height are readily measured as ΦR is blocked and unblocked. With ΦR unblocked, i.e. coupled to ΦG, the pulse height of the square wave, measured as a differential voltage between the upper and lower levels, GvGc G VEP (15) gives the ΦG post-coupled energy EGc and, very impor- tantly, the probability PG as well to within a multiplicative constant κ. After ΔVGc is acquired, ΦR is blocked ative constant κ. The measurement precisionGc G improved by using ac coupling rather than dc co Consequently, dc coupling ne from the coupling path by BR. The detector then samples the same annular region of ΦG but now the pulse height measurement GG VE (16) provides the beam’s grating-emergent energy EG, un- modified by coupling, to within the same multiplic of ΔV and of ΔV is op- timized by using real-time waveform averaging. More- over, the measurement precision of ΔVGc relative to ΔVG is significantly upling of the input signal. With ac coupling, as ΦR is alternately blocked and unblocked, the respective upper and lower levels of the square wave each shift by only ~1% or less relative to the full pulse height of the square wave. The confinement of the respective upper and lower levels to these narrow ranges of the vertical measurement scale effectively eliminates any artifactual effects of range-related non-linearity. Conversely, for dc coupling as ΦR is unblocked the square wave shifts upward on the vertical measurement scale by the bias voltage produced when a power PWRRa is deposited on the detector. cessitates an extremely linear response by the oscillo- scope in order to distinguish an actual transfer-related incremental change of ΔVGc relative to ΔVG from an arti- factual change arising from a non-linear response over the full range being used. (For example, with PWRRa ~ PWRGa, unblocking ΦR shifts the waveform on the vertical measurement scale by a bias that is ~100% of the square wave pulse height and the full utilized range in assessing ΔVGc relative to ΔVG is about two orders of magnitude greater for dc coupling than for ac coupling.) The vital significance of the ΔVGc and ΔVG pulse height measurements is that their ratio GG x VE Ge i Gc G VP which is the experimentally dete (17) rmined occupation value from a sequential pair of measurements ΔVGc and ΔVG, each of which is derived from an ave cycles. The subscript “ex” has been added to clearly raging over 128 pulse identify this quantity as experimentally determined. The subscript “i” denotes ΩG ex i as a single trial value for the particular installed grating G. A typical incremental change in ΔVGc relative to ΔVG for two sets of these averaged pulses may be on the order of ±1% (for G(3.16) or G(2.63), respectively). For beams of macroscopic power, these incremental changes are representative of enormous numbers of photons (~1011) added to or subtracted from ΦG in the annular sampling region as ΦR is coupled to ΦG. These changes are directly observable on the oscilloscope waveform as ΦR is blocked and unblocked. The oscilloscope also generates digital values for ΔVGc and for ΔVG from which each single trial value ΩG ex i is calculated for the particular installed grat- ing G. Ten single trial values ΩG ex i with that particular G are acquired and averaged to give a final reported value ΩG ex for that set of individual trials. The process is re- peated for the other two gratings to give the three tri- al-averaged values 2.63 3.16 ,, GexGex and 3.94Gex . An additional set of ten trials is acquired with no grating (NG) present which provides a control experiment value ΩNG ex. The resultant beam ΦNG is ordinary and should on coup trials, exhibit no net transfer hese NG a upling. In t G th should be observable in real time from a fixed-value attenuation filter is substituted for the gratings at position G in the apparatus. For any given setting of the variable attenuator AttG, that fixed-value filter transmits approximately the same power to the coupling path as do the gratings. The four sets of trials comprise a complete set. All of the single trials in the complete set, including the NG trials, are acquired with the same beam power PWRG on the coupling path. This is facilitated by minor adjust- ment of attenuator Att prior to acquiring each of the four sets to maintain some selected beam power PWRGa at the detector. The objective of this procedure is to exclude any artifactual power-related influences on the measurements contributing to the determinations of the three ΩG ex and the ΩNG ex. As a practical matter, the apparatus is most readily ini- tially aligned with either grating G(2.63) or G(3.16) in- stalled. Optimum coaxial alignment of ΦG and ΦR on the coupling pa ~1% change in pulse height as ΦR is alternately blocked and unblocked. It is important to note that deficiencies in fully achieving the various beam parameter criteria and accurate concentric alignment of ΦG and ΦR on the cou- pling path result in an incomplete equilibration transfer and a resultant experimental underestimate of the actual magnitude of the duality modulation [22]. Copyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL 920 5. Experimental Results The experimentally determined ΩGex values specific to the three gratings, 2.63 3.16 ,, GexGex and 3.95Gex , are plotted on the Figure 4 theoretically predicted ΩG th uation (7) a(equivalent to rt j from Eq an empirical obliquity correction nd inclusive of e no-grating control ine/mm grating G(installed 005 with a du 1 and the t th ). Th experiment value ΩNG ex is also depicted for comparison. With the 600 l2.63) in the apparatus, the experimentally determined occupation value 2.63 9 0.0024 Gex which, alternatively expressed as a “duality modulation” (deviation of Ω from unity), is +0.59% ± 0.24%. This result and the results 1. be 2.63 1. 0043 Gth low are given with ±SE standard error for n = 10 trials. The corresponding calculated theoretical value at jt = 2.63 is ality modulation of +0.43%. The significance of the experimentally deter- mined 2.63Gex is most appropriately assessed relative to the no-grating control experiment value 0.9988 0.0018 NGex . Since the theoretical prediction heoretical prediction of the no-grating control experiment 1 NGth , the operant hypothesis is at the true mean of 2.63Gex exceeds unity i.e. the true mean of 2.63Gth Gex . Accordingly, the trials fo ep acquired to the ind r 2.63Gex re statistically evaluated relative endent control experiment trials for a Gex in o e calcul a one-tailed t test to determine nfidence level. With the given experimental results, thated con- fidence level p = 0.015 isy supportive of the hy- pothesis that tean of 2.63 1 Gex th ighl e p c h ue mhe tr . Similarly, with the 500 line/mm G(3.16) grin- stalled, the value 3.16 0.9923 0.0019 Gex and the ex- perimentally measured duality modulation is 3.16 0.77 0.19%.0.9912 Gth giving a predicted dua- lity modulation of −0.88%. As ating sessing this result relative ean of ation used 3.95) re to beatistically distinguishable h this hypothesis is strongly rejected and we conclude that to s th for the previous ΩNGex, the theoretical prediction 3.16 1 Gth yields an operant hypothesi 3.16Gex is less than unity. Applying the same statistical evalu at the true m grating, the calculated confidence level p = 0.011 is highly supportive of the present hypothesis that the true mean of 3.16 1 Gex . Finally, the 400 line/mm grating G(sults in 3.95 0.99970.0023 Gex with a duality modulation of −0.03% ± 0.23%. Since jt = 3.95 is in the neighborhood of the jt = 4 diffraction null, there is no basis a priori for the true mean of G st 3.95 ex m unity. This contention is supported by the theoreti- 3.95 0.9985 Gth which closely ap- proximates ΩNG th = 1. Accordingly, a two-tailed t test is appropriate for comparing the set of 3.95Gex trials and the set of ΩNG The operant hypothesis then states that the true mean of 3.95Gex is significantly different from that of ΩNG exa calculated p = 0.76, the true means of 3.95Gex fro cally predicted ex trials. . However, wit and ΩNG ex are not statistically distinguishable. One additional statistical evaluation of interest can be performed with the abolts. We have a theoretical basis for 2.63 3.16GthGth ve resu . Consequently, we can pro- pose a hypothesis that the true mean of 2.63Gex exceeds that of 3.16 Gex y a one-tailed t test to find the relevant p confid and appl ence level. With a resultant p = 0.00016, the present hypothesis is supported at an even higher confidence level than that for either 2.63Gex or 3.16Gex relativlthough this hypothesis does not provide a conclusion with respect tolute, i.e. that the n of 2.63 1 Gex e to ΩNG ex. A o an abs true mea or that the true mean of 3.16 1 Gex , the confirmation of this hypothesis neces- sitates that at least one of the true means of 2.63Gex and 3.16Gex is not unity in violation of duality. The a of ΩG th F gratings G(2 uce enri and depl.95) is pre- di rrent experiment is to test for statisti- ca bove reported experimental results of ΩGex pro- vide for the determination of the three points plotted on the theoretical graphigure 4. The particular .63) and G(3.16) are used because they are theoretically predicted to respectively prodched eted beams at λ = 633 nm while G(3 cted to produce an ordinary beam at that wavelength. Moreover, in the interests of facilitating replication of the present experiment, all three gratings are commercially readily available. A detailed verification of the Figure 4 theoretical curve by the acquisition of a large number of experimental data points is certainly of interest. However, that detailed verification is clearly not possible with three data points nor is that the present intent of the authors. The primary objective of the cu lly significant violations of duality when particular resultant beams ΦG are coupled with a beam ΦR. Spe- cifically, G(2.63) and G(3.16) are predicted to prepare the resultant outgoing beams in a state not representable by duality. In the interest of eliminating potential systematic sources of experimental error, the respective resultant beams for all three gratings and for the NG control are maintained at the same power level for the complete set of trials. With this constraint of equivalent power, duality necessarily imposes a fundamental physical equivalence of the four resultant beams. Duality also forbids a net transfer for these or any other beams upon coupling with an independently generated beam. Nevertheless, when the four resultant beams are respectively coupled with ΦR, statistically significant net transfers consistently occur for 2.63G and 3.16G with positive and negative net transfers, respectively. In addition to the trials reported here, many hundreds of preliminary trials have been conducted. Various beam powers for ΦG and ΦR have been employed for these trials while maintaining the general coupling criteria. Several different gratings of each of the three types were used. Copyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL 921 Throughse prel ed here. An independent apparatus ha ly through rough entanglement of correlated quan- e duality violation presented here is tates of those en provides fo en pendent laser beam, the sfers either +0.59% or −0.77% of its endent beam for two of the gratings, er phenomenon is shown to be theoretically re out theiminary trials the results were con- sistent with those report s also been assembled that similarly demonstrates ΩG ex comparable to those of the present apparatus. 6. Discussion From a theoretical perspective there remains an important consideration relating to the demonstration of duality violation as a validation of local realism. The probabilistic interpretation is distinguished from local realism as a consequence of non-locality manifested not on duality but also th tum entities [25]. Th consistent with local realism. However, that leaves the dilemma of entanglement, seemingly conclusively con- firmed through Bell’s theorem [26] by reported experi- mental results [27,28], in support of the probabilistic interpretation despite compelling arguments to the con- trary [29,30]. Any viable physical representation must necessarily demonstrate a self-consistent basis supporting or refuting both duality and entanglement. In this regard, one of the present authors derived a lo- cally real representation of quantum mechanical states from fundamental principles that gives agreement with performed experiments for correlated photons and for correlated particles [31]. That representation, demon- strating locality for correlated entities, is based on non- conservation of probability for individual s tities in accord with the present locally real representa- tion demonstrating duality violation through non-conser- vation of probability in the diffraction process. Non- conservation of probability is of particular relevance in the present context. Clauser and Horne deduce that the locally real representations that can be excluded by Bell’s theo- rem are constrained by an implicit supplementary as- sumption of “no-enhancement” (for which insertion of a polarizer does not increase detection) [32]. That exclusion does not apply to the locally real representation in [31] where non-conservation of probability inherently pro- vides for enhancement. The resultant locally real repre- sentation is fully consistent with the underlying mathe- matical formalism of quantum mechanics. That formalism is “completed” [25] in the sense of maintaining local realism for quantum phenomena by admitting the degree of freedom to treat the relevant wave functions as relative entities of the field separable from resident particle-like entities. With this degree of freedom, specific examples of probability non-conservation emerge naturally. Experimentally, the configuration reported here, con- sisting of a single beam incident on a conventional Ronchi grating, provides for a modest duality modulation. Nev- ertheless, even this modest duality modulation translates to a readily measurable increment of beam power in the macroscopic cw regime. Moreover, the associated un- derlying locally real basis for this configuration r a particularly straightforward and compelling under- standing of a duality-violating phenomenon. There are, however, other configurations, e.g. [21], that exceed the present modest duality modulation. Ultimately, there is no inherent limitation on duality modulation in local realism. The utility of a duality modulation with very high en- richment or depletion at macroscopic powers can be ap- preciated from the transient coupling used in the present configuration. Transient coupling shows that interaction of a duality-modulated beam with an ordinary beam re- sults in a significant net transfer of energy from one of the beams to the other in the process. For example, a highly riched beam can be used to directly amplify a weak ordinary “signal” beam. Transient coupling equilibrates the two beams causing an enrichment of the signal beam that enhances conventional detectability of the signal’s wave modulations. Similarly, empty wave beams (or at least highly depleted beams) of macroscopic wave inten- sity would also be of utility in various applications such as probes of material samples where energy deposition into those samples by a probe beam must be minimized or eliminated. The interaction of an essentially empty probe beam with a sample would be made observable by equi- librating the post-interaction probe beam with an ordinary beam. That equilibration renders the wave of the post- interaction probe beam measurable by conventional de- tectors as a macroscopic power. 7. Conclusions The experiment reported here demonstrates violations of quantum duality with an apparatus reduced to the simplest of elements. A laser beam is prepared by passage through one of three particular Ronchi gratings. When the pre- pared beam is coupled to an inde prepared beam tran power to the indep respectively, whereas the power transfer associated with the prepared beam from the third grating is ≈0%. Quan- tum duality requires that the power transfer must be 0% for all three. Notably, the experiment is conducted with beams of macroscopic power. The resultant duality-violating power transfers, representing extraordinarily large numbers of ~1011 photons, are readily measurable by a conventional detector. The transfer phenomenon is robust and highly reproducible. That transf presentable from basic principles and the phenomenon is consistent with recent reports [10] and [11] of other performed experiments that also demonstrate violations of duality. Copyright © 2013 SciRes. JMP  D. MIRELL, S. MIRELL Copyright © 2013 SciRes. JMP 922 REFERENCES [1] P. A. M. Dirac, “The Principles of Quantum Mechanics,” Oxford University Press, Oxford, 1930. [2] L. Mandel, Physical Review, Vol. 134, 1964, pp. A10- A15. doi:10.1103/PhysRev.134.A10 [3] L. de Broglie, “Electrons et Photons,” Gauthier-Villars, Paris, 1928. [4] F. Selleri, Physics Letters A, Vol. 120, 1987, pp. 371-376. doi:10.1016/03 75-9601(87)90680-3 [5] A. Garuccio, K. A. Popper and J.-P. Vigier, Physics Let- ters A, Vol. 86A, 1981, pp. 397-400. doi:10.1016/0375-9601(81)90346-7 [6] J. R. Croca, A. Garuccio, V. L. Lepore and R. N. Moreira, Foundations of Physics Letters, Vol. 3, 1990, pp. 557-564. doi:10.1007/BF00666024 [7] M. Lai and J.-C. Diels, Journal of the Optical Society of America B, Vol. 9, 1992, pp. 2290-2294. doi:10.1364/JOSAB.9.002290 [8] K. R. Popper, “Quantum Theory and the Schism in Phys- ics,” Rowman and Littlefield, Totowa, [9] N. Bohr, Nature, Vol. 121, 1928, pp. 1982. 580-590. doi:10.1038/121580a0 [10] S. Kocsis, B. Braverman, S. Ravets, M. J. Stevens, R. P. Mirin, L. K. Shalm and A. M. Steinberg, Science, Vol. 332, 2011, pp. 1170-1173. doi:10.1126/science.1202218 [11] R. Menzel, D. Puhlmann, A. Heuer and W Proceedings of the National A . P. Schleic cademy of Sciences, Vol h, . 109, 2012, pp. 9314-9319. doi:10.1073/pnas.1201271109 [12] Y. Aharonov, D. Z. Albert and L. Vaidman, Ph tt.60.1351 ysical Review Letters, Vol. 60, 1988, pp. 1351-1354. doi:10.1103/PhysRevLe [13] G. J. Pryde, J. L. O’Brien, A. G. White, T. C. Ralph and H. M. Wiseman, Physical Review Letters, Vol. 94, 2005, Article ID: 220405. doi:10.1103/PhysRevLett.94.220405 [14] R. Mir, J. S. Lundeen, M. W. Mitchell, A. M. Steinberg, J. L. Garretson and H. M. Wiseman, New Journal of Physics, Vol. 9, 2007, Article ID: 287. doi:10.1088/1367-2630/9/8/287 [15] J. S. Lundeen and A. M. Steinberg, Physical Re ters, Vol. 102, 2009, Article ID: 020 view Let- 404. doi:10.1103/PhysRevLett.102.020404 [16] K. Yokota, T. Yamamoto, M. Ko Journal of Physics, Vol. 11, 2011, Article ID: 03 ashi and N. Imoto, New 3011. [17] H. M. Wiseman, New Journal of Physics, Vol. 9, 2007, Article ID: 165. [18] M. Rabinowitz, Modern Physics Letters B, Vol. 9, 1995, pp. 763-789. doi:10.1142/S0217984995000711 [19] M. Rabinowitz, International Journal of Theoretical Phy- sics, Vol. 52, 2013, pp. 668-678. doi:10.1007/s10773-012-1374-5 [20] M. Born, Zeitschrift für Physik, Vol. 37, 1926, pp. 863- 867. doi:10.1007/BF01397477 [21] D. J. Mirell and S. G. Mirell, Quantum Physics, Vol. 1, 2005. arXiv: quant-ph/0509028. [22] D. J. Mirell and S. G. Mirell, Quantum Physics, 2011. arXiv: 1107.1306v1. [23] J. W. S. Rayleigh, Philosophical Magazine, Vol. 14, 1907, pp. 60-65. [24] H. Paul, Reviews of Modern Physics, Vol. 58, 1986, pp 209-231. . doi:10.1103/RevModPhys.58.209 [25] A. Einstein, B. Podolsky and N. Rosen, Physical Review, Vol. 47, 1935, pp. 777-780. doi:10.1103/PhysRev.47.777 [26] J. S. Bell, Physics, Vol. 1, 1964, pp. 195-200. [27] J. F. Clauser and A. Shimony, Reports on Progress in Physics, Vol. 41, 1978, pp. 1881-1927. doi:10.1088/0034-4885/41/12/002 ical Review[28] A. Aspect, J. Dalibard and G. Roger, Phys Letters, Vol. 49, 1982, pp. 1804-1807. doi:10.1103/PhysRevLett.49.1804 [29] M. Ferrero, T. W. Marshall and E. Sa Journal of Physics, Vol. 58, 1990, p ntos, American p. 683-687. doi:10.1119/1.16400 [30] V. L. Lepore and F. Selleri, Foundation ters, Vol. 3, 1990, pp. 203-220. s of Physics Let- 10.1007/BF00666012doi: [31] S. G. Mirell, Physical Review A, Vol. 65, 2002, Article ID: 032102. doi:10.1103/PhysRevA.65.032102 [32] J. F. Clauser and M. A. Horne, Physical Review D, Vol. 10, 1974, pp. 526-535. doi:10.1103/PhysRevD.10.526
|