 Energy and Power Engineering, 2013, 5, 363-371 http://dx.doi.org/10.4236/epe.2013.55037 Published Online July 2013 (http://www.scirp.org/journal/epe) DSP Based Simulator for Speed Control of the Synchronous Reluctance Motor Using Hysteresis Current Controller Abdel-Karim Daud1, Basim Alsayid2 1Electrical and Computer Engineering Department, Palestine Polytechnic University (PPU), Hebron, Palestine 2Electrical Engineering Department, Palestine Technical University (PTU), Tulkarm, Palestine Email: daud@ppu.edu, b.alsayid@ptuk.edu.ps Received May 12, 2013; revised June 13, 2013; accepted June 20, 2013 Copyright © 2013 Abdel-Karim Daud, Basim Alsayid. This is an open access article distributed under the Creative Commons Attri- bution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT This paper presents the field oriented vector control scheme for synchronous reluctance motor (SRM) drives, where current controller followed by hysteresis comparator is used. The test motor has a star-connected wound stator and a segmental rotor of the multiple barrier type with an external incremental encoder to sense rotor position. The magnetic characteristics of this motor are described using 2D finite element method, which is used firstly for rotor design of SRM. The field oriented vector control, that regulates the speed of the SRM, is provided by a quadrature axis current com- mand developed by the speed controller. The simulation includes all realistic components of the system. This enables the calculation of currents and voltages in different parts of the voltage source inverter (VSI) and motor under transient and steady state conditions. Implementation has been done in MATLAB/Simulink. A study of hysteresis control scheme associated with current controllers has been made. Experimental results of the SRM control using TMS320F24X DSP board are presented. The speed of the SRM is successfully controlled in the constant torque region. Experimental results of closed loop speed control of the SRM are given to verify the proposed scheme. Keywords: Field Oriented Control; 2D Finite Element Method; SRM; Hysteresis Current Controller; DSP; MATLAB/Simulink 1. Introduction Synchronous reluctance motor (SRM) has recently at- tracted the efforts of a number of researchers and is gaining favor as a possible alternative for ac drives [1-4]. Since the converter fed SRM does not need a starting cage, an optimized rotor for synchronous performance can be designed. The simple and rugged structure allows high speed drives to be readily attained while the copper and iron losses confined into the stator allow the motor to be operated with high electric and magnetic loads with advantage on the torque/weight ratio. A drawback of these drives resides in the need of synchronization with the rotor position [5-7]. The complicated coupled nonlin- ear dynamic performance of SRM can be significantly improved using vector control theory [4,8-16] where torque and flux can be controlled separately. Simulations have helped the process of developing new systems in- cluding motor drives, by reducing cost and time. Simulation tools have the capabilities of performing dynamic simulations of motor drives in a visual envi- ronment so as to facilitate the development of new sys- tems [14,17,18]. In this work, the simulation of a field oriented con- trolled SRM drive system is developed using MAT- LAB/Simulink. The motor has a segmental rotor of the multiple barrier type with an external incremental encoder to sense rotor position. The simulation circuit will include all realistic components of the drive system. This enables the calcu- lation of currents and voltages in different parts of the inverter and motor under transient and steady state con- ditions. A closed loop control system with a PI controller in the speed loop has been designed to operate in con- stant torque region. A study of hysteresis control scheme associated with current controller has been made. Simu- lation results are given for the speed range in constant torque region of motor operation. Finally, the experi- mental verification obtained by using the DSP based C opyright © 2013 SciRes. EPE 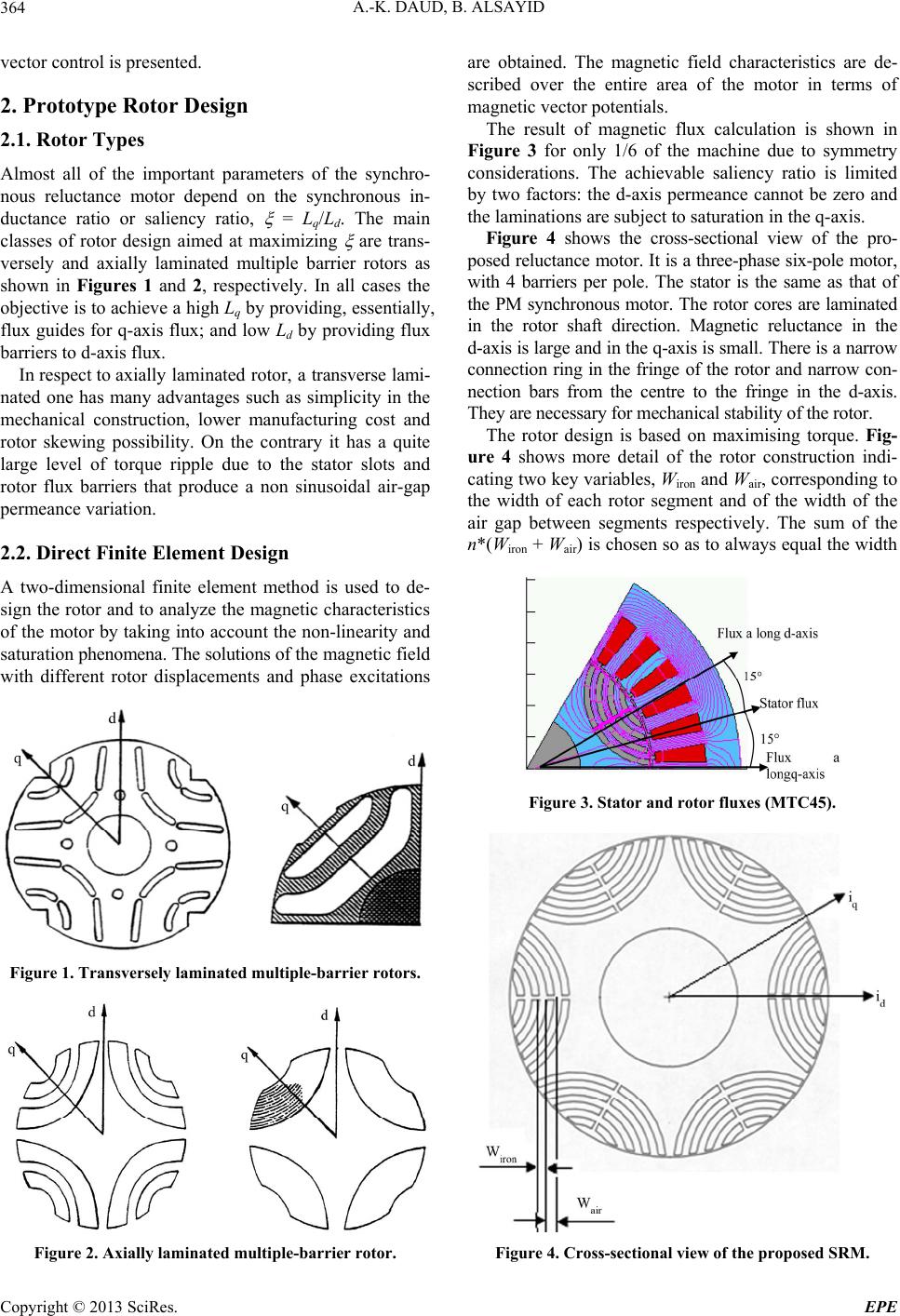 A.-K. DAUD, B. ALSAYID 364 vector control is presented. 2. Prototype Rotor Design 2.1. Rotor Types Almost all of the important parameters of the synchro- nous reluctance motor depend on the synchronous in- ductance ratio or saliency ratio, = Lq/Ld. The main classes of rotor design aimed at maximizing are trans- versely and axially laminated multiple barrier rotors as shown in Figures 1 and 2, respectively. In all cases the objective is to achieve a high Lq by providing, essentially, flux guides for q-axis flux; and low Ld by providing flux barriers to d-axis flux. In respect to axially laminated rotor, a transverse lami- nated one has many advantages such as simplicity in the mechanical construction, lower manufacturing cost and rotor skewing possibility. On the contrary it has a quite large level of torque ripple due to the stator slots and rotor flux barriers that produce a non sinusoidal air-gap permeance variation. 2.2. Direct Finite Element Design A two-dimensional finite element method is used to de- sign the rotor and to analyze the magnetic characteristics of the motor by taking into account the non-linearity and saturation phenomena. The solutions of the magnetic field with different rotor displacements and phase excitations Figure 1. Transversely laminated multiple-barrier rotors. Figure 2. Axially laminated multiple-barrier rotor. are obtained. The magnetic field characteristics are de- scribed over the entire area of the motor in terms of magnetic vector potentials. The result of magnetic flux calculation is shown in Figure 3 for only 1/6 of the machine due to symmetry considerations. The achievable saliency ratio is limited by two factors: the d-axis permeance cannot be zero and the laminations are subject to saturation in the q-axis. Figure 4 shows the cross-sectional view of the pro- posed reluctance motor. It is a three-phase six-pole motor, with 4 barriers per pole. The stator is the same as that of the PM synchronous motor. The rotor cores are laminated in the rotor shaft direction. Magnetic reluctance in the d-axis is large and in the q-axis is small. There is a narrow connection ring in the fringe of the rotor and narrow con- nection bars from the centre to the fringe in the d-axis. They are necessary for mechanical stability of the rotor. The rotor design is based on maximising torque. Fig- ure 4 shows more detail of the rotor construction indi- cating two key variables, Wiron and Wair, corresponding to the width of each rotor segment and of the width of the air gap between segments respectively. The sum of the n*(Wiron + Wair) is chosen so as to always equal the width Figure 3. Stator and rotor fluxes (MTC45). Figure 4. Cross-sectional view of the proposed SRM. Copyright © 2013 SciRes. EPE  A.-K. DAUD, B. ALSAYID 365 of one stator tooth (Wt) in order to limit, as much as pos- sible, pulsating fluxes (torque ripple)in the stator teeth. In practice, values of n = 1, 2 and 3 were investigated. For purposes of comparison between different geome- tries it is useful to define the ratio Kw = Wair/Wiron. Clearly, when Kw = 0, the rotor is assumed to be completely made of iron (no saliency). When Kw = 1 the rotor is con- structed of lamination segments in which the air space and lamination segments are equal. FEA for n = 1, 2 and 3 gave maximum torque for Kw = 1 and n = 3, in which Wair = Wiron = 1.86 mm. 2.3. Torque and Torque Ripple Three-phase motor currents have been considered to supply the stator expressed by Equation(1) and the re- sulting stator flux forms an electrical angle of 45° (15° mechanical) with q-axis, which gives a maximum torque curve (MTC45) (see Figure 3). 122sin 122sin 12 122sin 240 a b c I I I 106 A 00 A 106 A (1) where = 120˚ is the electrical angle corresponding to stator flux at 45° electric degrees from rotor flux, 122 A is maximum current for half stator slot. The same normal B-H characteristic is computed for stator and rotor mag- netic material. With FEA a value of 4.2 Nm of Torque has been calculated, it was the best value for different values of electrical angle between stator and rotor fluxes, which was verified experimentally. The torque ripple results from the non-sinusoidal air-gap permeance func- tion for the stator slots and rotor flux barriers; its estima- tion requires an accurate FEA with different stator-rotor relative positions. A few significant rotor positions, among infinite ones, have been considered in order to predict the torque ripple with a good accuracy. Five rotations have been considered, each rotation of 1 mechanical degree or 3 electrical degrees, which corre- spond to a half stator tooth pitch. The results of calculated torque for each position are obtained in Figure 5. It shows the torque ripple for a rotation of an electrical angle of 15° (equal to a me- chanical angle of 5°, six-pole motor). This is the angle of skewing of the rotor adopted to reduce torque ripple. The main dimensions of the test motor are shown in Table 1. It is a 6-pole sinusoidal synchronous reluctance motor (SRM). It has a star-connected wound stator, a segmental rotor of the multiple barrier type (see Figure 6) and external incremental encoder to sense rotor position. 3. SRM Drive System The well-known d-q model of AC machines is widely Figure 5. Torque ripple. Figure 6. Cross section of the synchronous reluctance ma- chine. Table 1. SRM parameters. Name Symbol Value Rated voltage Vn 220 V Rated torque Tn 5 Nm Rated current In 14.9 A Rated speed nn 1000 RPM Maximum speed nmax 6000 RPM Number of pole pairs P 3 Stator resistance Rs 0.3 Ω q-axis Inductance Lq 0.009 H d-axis Inductance Ld 0.004 H Motor Inertia J 0.0755 kgm2 Copyright © 2013 SciRes. EPE  A.-K. DAUD, B. ALSAYID Copyright © 2013 SciRes. EPE 366 used for simulation purposes. Based on the assumption that the stator windings are sinusoidally distributed, the d-q model is a powerful tool for dynamic simulation of most AC machines including the reluctance synchronous machine. The d-q reference frame equations describing the mo- tor are: 10 1 0 q q q d d v v L d d d r qq q dd q rdd L R LL L ii ii L tR LL (2) where id and iq are the d and q axis stator currents, Ld and Lq are the stator phase d-axis and q-axis winding self in- ductance respectively; R is the stator winding resistance; r is the rotor electrical speed; vd and vq are the stator voltages expressed in the dqreference frame. The inverter frequency is related as follows r P (3) where P is the number of pole pairs. The electromagnetic torque equation is given by edqdq LLii 3 2 TP (4) For maximum torque per ampere id = iq, therefore the currents id and iq can be obtained from Equation (5) as follows: 3 2 e dq T PL L d i (5) The equation of the motor dynamics is dd eLr r TT tBJw (6) TL stands for external load torque. B represents the damping coefficient and J is the moment of inertia of the rotor. The Equations (2), (4) and (6) constitute the whole control model of the SRM. A system configuration of a vector-controlled SRM drive system is shown in Figure 7. The dynamic d q modeling is used for the study of motor during transient and steady state. It is done by converting the dqo variables to three phase currents by using inverse Parks transformation [16-18]. SRM is fed form a voltage source inverter (VSI) with current control. The control is performed by regulating the flow of current through the stator of the motor. Cur- rent controllers are used to generate gate signals for the inverter. Proper selection of the inverter devices and se- lection of the control technique will guarantee the effi- ciency of the drive. In the vector control scheme, torque control can be carried out by suitable regulation of the stator current vector; this implies that accurate speed control depends on how well the current vector is regulated. In high-per- formance vector drives, a current-control loop, with a considerably high bandwidth, is necessary to ensure ac- curate current tracking, to shorten the transient period as much as possible and to force the voltage source inverter (VSI) to equivalently act as a current source amplifier within the current loop bandwidth. In this work, a hys- teresis-band current controlled VSI is used. This control- ler will generate the reference currents with the inverter within a range which is fixed by the width of the band gap. In this controller the desired current of a given phase Figure 7. SRM vector-controlled drive system.  A.-K. DAUD, B. ALSAYID 367 (a,b and c) is summed with the negative of the measured current (ia, ib and ic). When the current error exceeds a predefined hysteresis band, the upper switch in the half-bridge is turned off and the lower switch is turned on. As the current error goes below the hysteresis band, the opposite switching takes place. The principle of hysteresis band current control is illustrated in Figure 8 [4,16]. iii Speed controller calculates the difference between the reference speed ( *) and the actual speed ( ) producing an error, which is fed to the PI controller. PI controllers are used widely for motion control systems. Speed con- trol of motors mainly consist of two loops the inner loop for current (band hysteresis current controller) and the outer loop for speed (speed controller) as shown in Fig- ure 7. The order of the loops is due to their response, how fast they can be changed. This requires a current loop at least 10 times faster than the speed loop. An in- cremental encoder is used as a position sensor. Control loops in the actual drive system, shown in Fig- ure 7, are implemented in software on Texas Instruments (TMS320F24X) processor and executed with a cycle period of 70s. The flow chart of this program is shown in Figure 9. At switching on, the program initializes the hardware registers, I/O ports are then pre-set to their initial states, the inverter, ADC converters, position sensor (optical encoder) and software variables. Then it initializes the speed calculation and hysteresis regulators. The system now completes all initializations and starts the main pro- gram which requires a computational time of 70s of period cycle. The main program will first calculate actual speed of the motor ( ), read reference speed ( *) and actual cur- rents (ia, ib and ic) from ADCs. Errors are then saved and new errors are calculated. Speed regulator is realized by a discrete PI. Figure 8. Hysteresis current controller. Figure 9. System flow diagram. Calculation of q i and d in the rotating reference frame is done. Then it will read position from the en- coder. Based on rotor position, three-phase reference currents (a i i , b i and c i ) in the stationary reference frame are calculated. This is followed by the execution of cur- rents loop and resulting controlled signals are sent to the inverter. Write DAC and wait end cycle are finally exe- cuted. 4. Simulation in Simulink The SRM drive simulation was built in several steps like dqo variables transformation to abc phase, calculation torque and speed, control circuit, inverter and SRM. The dqo variables transformation to abc phase is built using the reverse Parks transformation. For simulation purpose the voltages are the inputs and the current are output. Using all the drive system blocks, the complete system block has been developed as shown in Figure 10. The system built in Simulink for a SRM drive system has been tested with the Hysteresis current control method at Copyright © 2013 SciRes. EPE  A.-K. DAUD, B. ALSAYID 368 we (rad/s) vb c (V ) v + - vb c theta idqsr i*abc stationary dq to ab c ISP Beta iq id rotating idq 45 i*q i*d the idqsr rotatin g dq to stationary dq Discrete, s = 1e-005 s pow ergui pi output 1.3 load torque PI iqr iqdsr1 pi/4 idr ia bc real i*abc reference iabc iref va vb vc hysteresi s current controll er e rro r in x X-Y Signal Scope iabcreal To Workspace2 speed To Workspace Te Workspace3To iabcreferenc To Workspace1 T e (N.m) m A B C Tm Synchronous Reluctance Ma chin e wi th zero magnetic flux Step1 Step 0 Speed Ref1 157 Speed Ref 3 3 ? Doubl e cli ck here for more in fo <Elect romagnet ic t orque Te (N* m )> <Rot or speed wm (rad/ s)> <Rot or angle thet am (rad)> Figure 10. Synchronous reluctance motor drive system in Simulink. 30 the constant torque region of operation. The motor parameters used for simulation are given in Table 1. Figure11 shows the real three phase currents drawn by the motor as a result of the hysteresis current control. The currents are obtained using Park’s reverse transformation. It is clear that the current is non-sinu- soidal at the starting and becomes sinusoidal when the motor reaches the controller command speed at steady state. Figure 12 shows a variation of the speed with time. The steady state speed is the same as that of the com- manded reference speed. Figure 13 shows the developed torque of the motor. The starting torque is the rated torque. The steady state torque is about 1.3 Nm. Figure 14 shows the real three phase currents drawn by the motor as a result of the hysteresis current control, when the motor changes its speed from 1000 rpm to −1000 rpm with a load torque of 1.3 Nm. It is clear that the currents are inversed due to the speed variation from 1000 to −1000 rpm. The speed performance is shown in Figure 15 for this case. The steady state speed is the same as that of the commanded reference speed. Figure 16 shows the developed torque of the motor for the speed variation from 1000 to −1000 rpm. The starting torque is the rated torque (5 Nm). The steady state torque is about 1.3 Nm in positive and negative opera- tion of the motor. 5. Experimental Results A DSP based PC board integrated system (TMS320F24X DSP board), is used for vector control of SRM drive [14]. The schematic diagram of the hardware implementation is shown in Figure 17. Feedback signals to the controller board are the actual motor currents and the rotor position angle. The currents are measured by the Hall-effect transducers. The currents are then buffered and fed to the A/D ports of the controller board. The motor shaft posi- 00.5 1.0 1.5 2 -30 -20 -10 0 10 20 time (s) iabc (A) Figure 11. Actual phase currents with hysteresis control at 1000 rpm with 1.3 N·m. 120 00.5 1.01.52 0 20 40 60 80 100 time (s) speed (rad/s) Figure 12. Dynamic performance for a step variation of the reference speed from 0 to 1000 rpm ( = 105 rad/s) with a torque load of 1.3 N·m. 6 00.5 1.0 1.52 0 1 2 3 4 5 torque (Nm) time s Figure 13. Developed torque for a step variation of the ref- erence speed from 0 to 1000 rpm (1.3 N·m load torque). Copyright © 2013 SciRes. EPE  A.-K. DAUD, B. ALSAYID 369 00.5 1.01.5 2.0 2.53 -30 -20 -10 0 10 20 30 time s iabc (A) ia ib ic Figure 14. Inversion of actual phase currents due to a step variation of a speed from 1000 rpm to −1000 rpm with a torque load of 1.3 N·m. 00.5 1.0 1.5 2.0 2.53 -150 -100 -50 0 50 100 150 time (s) speed (rad/s) Figure 15. Dynamic performance for a step variation of the speed from 1000 rpm to −1000 rpm ( = −105 rad/s) with a torque load of 1 N·m. 00.5 1.0 1.5 2.0 2.5 3.0 -6 -4 -2 0 2 4 6 time (s) torque (Nm) Figure 16. Developed torque with hysteresis control for a step variation of the speed from 1000 rpm to −1000 rpm (1 N·m load torque). tion is measured by an optical incremental encoder in- stalled at the motor shaft. The commutating signals for the drive pulses have also been generated by the hystere- sis controller. The control algorithm has been imple- mented via the controller board using assembly language programming. A series of experiments has been carried out to evalu- ate the performances of the proposed vector controlled SRM drive system. Different sample results are pre- sented in the following figures. Figure 18 demonstrates the actual phase current ia wave form at speed 1500 rpm for a load of 2 Nm. The experimental evaluation of speed with load as pa- rameter of DSP based SRM drive is shown in Figure 19. It shows the step speed response of 1000 rpm of the pro- posed system for a load of 1.3 Nm. In Figure 20, the behaviour of the current of phase A is shown during the inversion of speed from 1000 RPM to −1000 rpm with load torque of 2 Nm. Figure 21 shows the response of the drive to a step variation of the reference speed from 1000 to −1000 rpm with a load Figure 17. The hardware schematic of experimental system. Figure 18. Actual phase current ia wave form at 1500 rpm for a load of 2 N·m. Copyright © 2013 SciRes. EPE  A.-K. DAUD, B. ALSAYID 370 Figure 19. Experimental speed responses of SRM drive for step variation from 0 to 1000 rpm with load torque of 1.3 N·m. Figure 20. Inversion of actual speed and actual phase cur- rent ia wave forms due to a step variation of the reference speed from 1000 rpm to −1000 rpm (load Torque of 2 N·m). Figure 21. Dynamic performance for a step variation of the reference speed from 1000 rpm to −1000 rpm (load torque of 1 N·m). torque of 1 Nm. 6. Conclusions A rotor for a reluctance motor has been designed using 2D finite element method. The maximum torque has been found to be 4.2 Nm. The results obtained by FEA seem to be valid because, after the construction of the rotor, experimental results show that the maximum torque is about 4.2 Nm and the torque ripple with posi- tion is very closed to the results obtained by FEA. A MATLAB/SIMULINK simulation model has been proposed for closed loop speed control with internal cur- rent loop using hysteresis controllers. The experimental results show that the proposed field oriented vector con- trolled SRM drive can handle the effects of step change in reference speed and parameter variations. The overall system performances are quite good in terms of dynamic, transient and steady-state responses. Simulation and experimental results show that the pro- posed control scheme guarantees stable and robust re- sponse of the SRM drive, under a wide range of operat- ing conditions. Subsequently, it can be utilized in high performance motion control applications. REFERENCES [1] H. Kiriyama, S. Kawano, Y. Honda, T. Higaki, S. Mori- moto and Y. Takeda, “High Performance Synchronous Reluctance Motor with Multi-Flux Barrier for the Appli- ance Industry,” The 1998 IEEE Industry Applications Conference, Thirty-Third IAS Annual Meeting, St. Louis, 12-15 October 1998, pp. 111-117. [2] Malan, M. J. Kamper and P. N. T. Williams, “Reluctance Synchronous Machine Drive for Hybrid Electric Vehi- cle,” IEEE International Symposium on Industrial Elec- tronics, Pretoria, 7-10 July 1998, pp. 367-372. [3] J. Malan and M. J. Kamper, “Performance of a Hybrid Electric Vehicle Using Reluctance Synchronous Machine Technology,” IEEE Transactions on Industry Applica- tions, Vol. 37, No. 5, 2001, pp. 1319-1324. [4] G. K. Dubey, “Fundamentals of Electrical Drives,” Alpha Science, Temple City, 2001. [5] J.-M. Park, S.-J. Park, M.-M. Lee, J.-S. Chun and J.-H. Lee, “Rotor Design on Torque Ripple Reduction for a Synchronous Reluctance Motor with Concentrated Wind- ing Using Response Surface Methodology,” IEEE Tran- sactions on Magnetics, Vol. 42, No. 10, pp. 3479-3481. [6] S. B. Kwon, S. J. Park and J. H. Lee, “Optimum Design Criteria Based on the Rated Watt of a Synchronous Re- luctance Motor Using a Coupled FEM and SUMT” IEEE Transactions on Magnetics, Vol. 41, No. 10, 2005, pp. 3970-3972. doi:10.1109/TMAG.2005.855180 [7] J. Rizk, M. H. Nagrial and A. Hellany, “Optimum Design Parameters for Synchronous Reluctance Motors,” Pro- ceedings of the 14th International Middle East Power Systems Conference (MEPCON’10), Egypt, 19-21 De- Copyright © 2013 SciRes. EPE  A.-K. DAUD, B. ALSAYID Copyright © 2013 SciRes. EPE 371 cember 2010, Article ID: 290. [8] N. Bianchi, S. Bolognani, D. Bon and M. D. Pre, “Torque Harmonic Compensation in a Synchronous Reluctance Motor,” IEEE Transactions on Energy Conversion, Vol. 23, No. 2, 2008, pp. 466-473. [9] F. Fernandez-Bernal, A. Garcia-Cerrada and R. Faure, “Efficient Control of Reluctance Synchronous Machines,” Industrial Electronics Society, 1998. IECON ’98. Pro- ceedings of the 24th Annual Conference of the IEEE, Aachen, 31 August-4 September 1998, pp. 923-928. [10] R. E. Betz, R. Lagerquis M. Jovanovic, T. J. E. Miller and R. H. Middleton, “Control of Synchronous Reluctance Machines,” IEEE Transactions on Industry Applications, Vol. 29, No. 6, 1993, pp. 1110-1121. doi:10.1109/28.259721 [11] L. Xu and J. Yao, “ACompensated Vector Control Scheme of a Synchronous Reluctance Motor Including Saturation and Iron Loss,” IEEE Transactions on Industry Applications, Vol. 28, No. 6, 1992, pp. 1330-1338. doi:10.1109/28.175285 [12] J. C. Kim, J. H. Lee, I. S. Jung and D. S. Hyun, “Vector Control Scheme of Synchronous Reluctance Motor Con- sidering Iron Core Loss,” IEEE Transactions on Magne- tics, Vol. 34, No. 5, 1998, pp. 3522-3525. doi:10.1109/20.717831 [13] R. E. Betz, M. Jovanovic, R. Lagerquist and T. J. E. Miller, “Aspects of the Control of Synchronous Reluc- tance Machines including Saturation and Iron Losses,” Industry Applications Society Annual Meeting, 1992. Con- ference Record of the 1992 IEEE, Houston, 4-9 October 1995, pp. 456-463. [14] A.-K. Daud, B. Alsayid and A. Zaidan, “DSP Based Simulator for Field Oriented Control of the Surface Per- manent Magnet Synchronous Motor Drive,” International Journal of Circuits, Systems and Signal Processing, Vol. 6, No. 1, 2012, pp. 29-37. [15] M. H. Rashid, “Power Electronics, Circuits, Devices and Applications,” Pearson Prentice Hall, Upper Saddle River, 2004. [16] B. K. Bose, “Modern Power Electronics and AC Drives,” Prentice Hall, Upper Saddle River, 2002. [17] C.-M. Ong, “Dynamic Simulation of Electric Machinery Using Matlab/Simulink,” Prentice Hall, Upper Saddle River 1998. [18] M. A. Fellani and D. E. Abai, “Matlab/Simulink-Based Transient Stability Analysis of a Sensorless Synchronous Reluctance Motor,” World Academy of Science, Engi- neering and Technology, Vol. 68, 2010, pp. 1472-1476.
|