Int. J. Communications, Network and System Sciences, 2010, 3, 945-953
doi:10.4236/ijcns.2010.312129 Published Online December 2010 (http://www.SciRP.org/journal/ijcns)
Performance Evaluation and Analysis of Switching
Algorithms in MIMO-OFDM System with Ideal and
Non-Ideal CSI
Yosra Mlayeh, Fethi Tlili, Fatma Rouissi, Ilham Ouachani, Adel Ghazel
CITRA’COM Research Laboratory, Engineering School of Communications (SUP’COM), Tunis, Tunisia
Received September 12, 2010; revised October 15, 2010; accepted November 17, 2010
Abstract
In this paper we analyzed the bit error rate performance of a switching algorithm between spatial multiplex-
ing and diversity for an OFDM MIMO system with ideal channel state information. The effect of channel
estimation error was studied and we verified by simulations that the spatial multiplexing outperforms the
switching algorithm. Given that the switching algorithm is based on the comparison of the channel matrix
Demmel condition number to a threshold, its accuracy is compromised when channel estimation error in-
creases. As a first intuitive solution, we proceeded to the adaptation of the threshold, but this didn’t lead to a
pertinent improvement for the main reason that channel estimation errors did affect the MIMO techniques
which use different constellation. Based on that, we proposed a new estimation technique that improved the
bit error rate performance significantly.
Keywords: MIMO Diversity, Spatial Multiplexing, OFDM, Demmel Condition Number, Switching Algorithm,
Channel Estimation
1. Introduction
MIMO systems, with the integration of the spatial di-
mension, represent a good solution to improve the rate
and the robustness of transmission systems without in-
creasing the bandwidth of the system [1]. In addition,
using OFDM with MIMO allows simplifying the equali-
zation at the receiver [2]. MIMO-OFDM techniques
were introduced by the IEEE 802.16e-2005 specifica-
tions as a solution to improve the quality of service [3].
MIMO diversity (MD) and Spatial Multiplexing (SM)
are the two most known techniques used in MIMO
channels. Diversity techniques use two or more antennas
in the transmitter and the receiver side to improve the
wireless link quality and are not designed to increase the
peak data rate of the system [4]. An effective and simple
transmit diversity scheme namely Space Time Block
Coding (STBC) is proposed by Alamouti [5]. It encodes
the signal through two transmit antennas and in time to
enhance significantly the BER while preserving a unit
code rate. STBC has been generalized for more than two
antennas in [6].
In addition, spatial multiplexing techniques offer
higher peak throughput by transmitting independently
and separately encoded data signals from each of the
multiple transmit antennas [7,8].
Furthermore, when the MIMO technique is selected
based on feedback information about the channel state,
this can lead to higher link robustness. This aspect in-
volves studying appropriate adaptation algorithms al-
lowing the selection of the most appropriate MIMO
technique for given channel conditions. The transmitter
blocs’ specifications such as the MIMO technique and
the modulation scheme are adjusted according to the
current state of the wireless mobile channel instead of
being designed based on the worst case scenario. This
approach provides a much more efficient use of the
available resources and gives a practical cognitive radio
strategy.
This is especially true for the case of a MIMO-OFDM
system since it is very flexible and there are a great
number of parameters which can be adapted as the usual
modulation, the coding scheme and the MIMO scheme.
Several Adaptation Algorithms are proposed to en-
hance system performances in terms of Bit Error Rate
(BER) [9-12]. Other algorithms are proposed to maxi-

946 Y. MLAYEH ET AL.
mize capacity gains [13-17].
To enhance system performances, the MIMO switch-
ing technique was discussed for a fixed data rate in case
of narrowband MIMO channels [9-11]. Either multi-
plexing or diversity was chosen based on the instantane-
ous channel state and the decision is conveyed back to
the transmitter via a low-rate feedback channel. The
Demmel condition number of the instantaneous channel
matrix was proposed as a parameter based on the mini-
mum Euclidean distance of constellations in order to
characterize the suitability of a given instantaneous
channel matrix for SM compared to MIMO Diversity. In
[12], the authors have studied the suitability of a com-
plex 2 × 2 MIMO-OFDM channel matrix for SM using
instantaneous measurements of its channel Demmel con-
dition number in several indoor environments.
Other works are interested to enhance the capacity
gains using adaptation algorithms, where the selection
criterion is based on the knowledge of the Signal to
Noise Ratio (SNR) and the determinant of MIMO chan-
nel matrix [13,14]. These works focus primarily on the
case of delay insensitive applications for which throughput
maximization is the criterion for adaptation, and examine
performances of the adaptive MIMO-OFDM system in a
realistic outdoor environment, modeled using ray tracing
software.
In [15], it was shown that at the same spectral effi-
ciency, Alamouti’s STC combined with maximum-ratio
combining at the receiver significantly outperforms the
2 × 2 spatial multiplexing scheme at high values of the
signal-to noise ratio (SNR). In this work, the selection of
the MIMO option is included in link adaptation to maxi-
mize network capacity, and operating SNR regions are
determined for different modulation, coding and MIMO
combinations.
Moreover, the impact of mutual antenna coupling on
the ergodic capacities of statistical beamforming and
spatial multiplexing transmission strategies is analyzed
[16,17]. Adaptive switching between combinations of
transmission strategies and antenna array configurations
(using reconfigurable antenna arrays) is shown to pro-
duce maximum capacity gains.
Hence, we deduce that the approach of physical layer
adaptation is becoming more and more an interesting
subject in the telecommunication area. Nevertheless,
previous works assumes ideal Channel State Information
(CSI) and no feedback delay.
So, to evaluate the performances of theses algorithms
while considering practical contexts, this paper considers
the effect of channel estimation errors on a 2 × 2 MIMO
OFDM switching algorithm.
To summarize, using the Demmel condition number as
a selection metric, we:
1) Evaluate performances of OFDM switching algo-
rithm in ideal CSI.
2) Study the effect of channel estimation on switching
algorithm performances.
3) Propose three methods to improve performances of
this switching algorithm in practical contexts with non
ideal CSI.
This paper is organized as follows: the second section
describes the OFDM-MIMO based system following
with switching algorithm. The third section deals with
MIMO-OFDM channel estimation effect on the switch-
ing technique. After a brief review of estimation methods,
performances of the switching algorithm with non ideal
CSI are showed and analyzed. Then, two solutions are
proposed to improve these performances. The first one,
although its additional complexity, reaches the perform-
ances of ideal CSI case. The second one enhances con-
siderably performances of switching algorithm without
any change in the receiver design. In Section 4, Conclu-
sion and perspectives of the work are outlined.
2. MIMO-OFDM System with Switching
Algorithm
2.1. System Model
In this work, we consider The MIMO-OFDM transceiver
following WiMAX standard as depicted in Figure 1.
Different blocs are defined following 802.16e -2005 spe-
cifications [3].
In the transmitter side, data are encoded using convo-
lutional codes. After bitwise interleaving, bits are
mapped to M-QAM symbols. Then, the MIMO encoder
is fed and OFDM samples are computed via the IFFT.
Finally, the cyclic prefix is added.
The MIMO module can be used to spatial Multiplex-
ing, Spatial Diversity or beamforming. In this paper, a
switching algorithm is used to select between Spatial
Multiplexing and MIMO Diversity in order to enhance
performances of the MIMO system in terms of BER. To
compare performances offered by proposed algorithms to
that proposed in the literature, we adopt 2x2 MIMO ar-
chitecture, which means that we use two antennas in the
transmitter side


2
t
N

and two antennas


2
r
N

in the receiver one.
SM Techniques are known to increase the throughput
at a given SNR. The base station transmits independent
data streams from each transmit antenna to the subscriber’s
stations. It could be implemented using Zero-forcing
(ZF), Maximum likelihood or MMSE (Minimum Mean
Square Error) detectors [8]. The ZF detector inverts the
channel matrix to detect the transmitted symbols. Even
though it suffers from poor performances at low SNR, it

Y. MLAYEH ET AL.
947
b
k


k
s
Tx1
Bloc
interleaving
Mapping
MIMO
module:
SM or MDIFFT
Randomization
and
Convolutional
coding
IFFT P/S
converter
P/S
converter
Tx2
Rx1
Bloc
desinterleav-
ing
DeMapping
FFT
FFT S/P
converter
S/P
converter
Rx2
CP
insertion
CP
insertion
CP
removal
CP
removal
Convolutional
decoding and
de-randomization
MIMO
module :
SM or MD

k
b
Figure 1. Block diagram of the MIMO- OFDM transceiver.
is employed in this work as the detection scheme because
it has a very small complexity and does not depend on
the modulation type.
MD uses two or more antennas in the transmitter and
the receiver side to improve the wireless link quality.
The main idea behind antenna diversity techniques is to
produce different replicas of the transmitted signal to the
receiver [5,6]. These replicas are sent over the propaga-
tion channel. Due to this redundancy, the receiver can
decode the transmitted signal even in fading conditions,
as long as they all do not fade simultaneously. In this
work, we use the Alamouti code as a Space Time Block
Code (STBC).
2.2. Switching Between SM and MD
Link adaptation plays a central role in regulating the use
of radio resources. The idea behind switching algorithm
is to dynamically adapt the MIMO technique and the
modulation scheme to channel conditions in order to
achieve the highest Bit Error Rate (BER) performances.
Several channel metrics were proposed as selection crite-
ria. The well-known metrics are Signal to Noise ratio,
channel matrix determinant [13,14], the minimum Eucli-
dean Distance [9,10] and the Demmel condition number
[11,12]. In this work, the OFDM switching between the
SM and the DM techniques is based on the Demmel
condition number

d

K
criterion. It can provide infor-
mation about the invertibility of the channel which pro-
vides knowledge about its suitability for use in either SM
or MD operational modes [18]. The Demmel condition
number for a random real or complex matrix H is de-
fined in [19] as:
 
min
nF
dn n
K

H H
H
(1)
where Hn denotes the MIMO channel matrix of the nth
subcarrier,

min n


H
refers to the minimum singular
value of Hn and refers to the Frobinüs norm.
F
The Demmel condition number measures how ill
posed a given matrix is. Physically, in [7] it was shown
that this metric provides a comparison between the
minimum signal constellation distance needed to support
SM and MD modes of operation for a given channel.
Considering the expression of the Demmel condition
number given by Equation (1), one sufficient condition
that multiplexing will be better than diversity for a given
channel matrix is given in [9] by:

min,
min,
SMt
dn
M
Dt
d
d
KH, (2)
where dmin,SMt and dmin,MDt are minimum Euclidean dis-
tances at the transmitter side in case of SM and MD, re-
spectively.
The switching algorithm adds an extra processing in
either the transmitter or the receiver. The decision is first
computed by the receiver, for every subcarrier, then, it is
sent back to the transmitter via a low rate feedback
channel. Depending on the received decision vector, the
transmitter will switch between the two MIMO tech-
niques.
To ensure that an overall rate of R bits per codeword is
maintained, symbols are derived from a constellation
with R bits per symbol when MD technique is chosen
and with RNT bits per symbol when SM is chosen.
Given that every subcarrier has its appropriate channel
matrix and consequently its Demmel condition number,
the decision is taken for every subcarrier. The switching
algorithm will select the adequate MIMO technique in
every subcarrier.
2.3. Performance Evaluation with Ideal CSI
Performances in terms of BER of Demmel condition
number was evaluated in case of narrowband channels in
[9]. In order to evaluate these performances of switching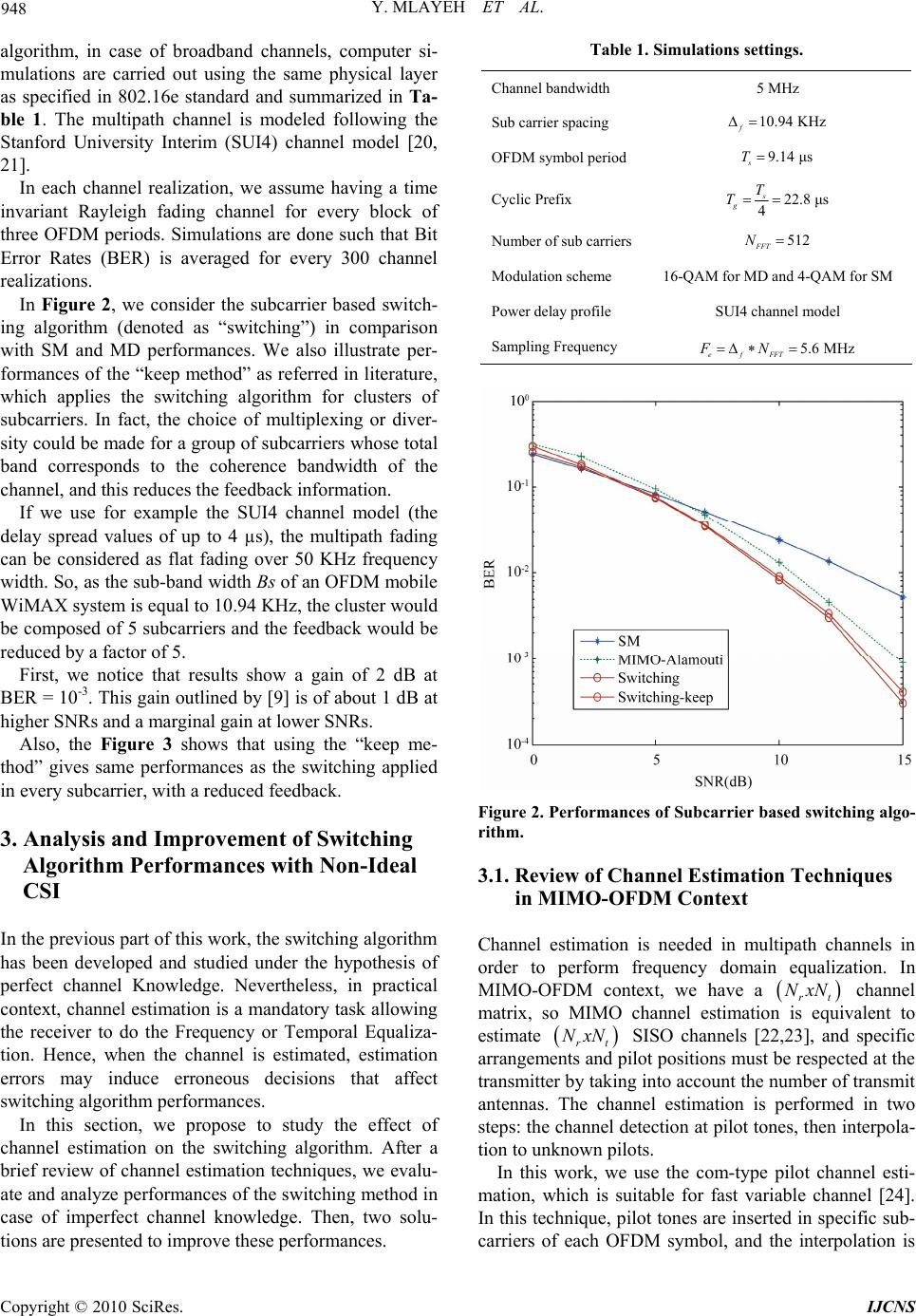

948 Y. MLAYEH ET AL.
algorithm, in case of broadband channels, computer si-
mulations are carried out using the same physical layer
as specified in 802.16e standard and summarized in Ta-
ble 1. The multipath channel is modeled following the
Stanford University Interim (SUI4) channel model [20,
21].
In each channel realization, we assume having a time
invariant Rayleigh fading channel for every block of
three OFDM periods. Simulations are done such that Bit
Error Rates (BER) is averaged for every 300 channel
realizations.
In Figure 2, we consider the subcarrier based switch-
ing algorithm (denoted as “switching”) in comparison
with SM and MD performances. We also illustrate per-
formances of the “keep method” as referred in literature,
which applies the switching algorithm for clusters of
subcarriers. In fact, the choice of multiplexing or diver-
sity could be made for a group of subcarriers whose total
band corresponds to the coherence bandwidth of the
channel, and this reduces the feedback information.
If we use for example the SUI4 channel model (the
delay spread values of up to 4 µs), the multipath fading
can be considered as flat fading over 50 KHz frequency
width. So, as the sub-band width Bs of an OFDM mobile
WiMAX system is equal to 10.94 KHz, the cluster would
be composed of 5 subcarriers and the feedback would be
reduced by a factor of 5.
First, we notice that results show a gain of 2 dB at
BER = 10-3. This gain outlined by [9] is of about 1 dB at
higher SNRs and a marginal gain at lower SNRs.
Also, the Figure 3 shows that using the “keep me-
thod” gives same performances as the switching applied
in every subcarrier, with a reduced feedback.
3. Analysis and Improvement of Switching
Algorithm Performances with Non-Ideal
CSI
In the previous part of this work, the switching algorithm
has been developed and studied under the hypothesis of
perfect channel Knowledge. Nevertheless, in practical
context, channel estimation is a mandatory task allowing
the receiver to do the Frequency or Temporal Equaliza-
tion. Hence, when the channel is estimated, estimation
errors may induce erroneous decisions that affect
switching algorithm performances.
In this section, we propose to study the effect of
channel estimation on the switching algorithm. After a
brief review of channel estimation techniques, we evalu-
ate and analyze performances of the switching method in
case of imperfect channel knowledge. Then, two solu-
tions are presented to improve these performances.
Table 1. Simulations settings.
Channel bandwidth 5 MHz
Sub carrier spacing 10.94 KHz
f

OFDM symbol period 9.14 μs
s
T
Cyclic Prefix 22.8 μs
4
s
g
T
T
Number of sub carriers512
FFT
N
Modulation scheme 16-QAM for MD and 4-QAM for SM
Power delay profile SUI4 channel model
Sampling Frequency 5.6 MHz
efFFT
FN 
Figure 2. Performances of Subcarrier based switching algo-
rithm.
3.1. Review of Channel Estimation Techniques
in MIMO-OFDM Context
Channel estimation is needed in multipath channels in
order to perform frequency domain equalization. In
MIMO-OFDM context, we have a channel
matrix, so MIMO channel estimation is equivalent to
estimate

rt
NxN



rt
NxN SISO channels [22,23], and specific
arrangements and pilot positions must be respected at the
transmitter by taking into account the number of transmit
antennas. The channel estimation is performed in two
steps: the channel detection at pilot tones, then interpola-
tion to unknown pilots.
In this work, we use the com-type pilot channel esti-
mation, which is suitable for fast variable channel [24].
In this technique, pilot tones are inserted in specific sub-
carriers of each OFDM symbl, and the interpolation is o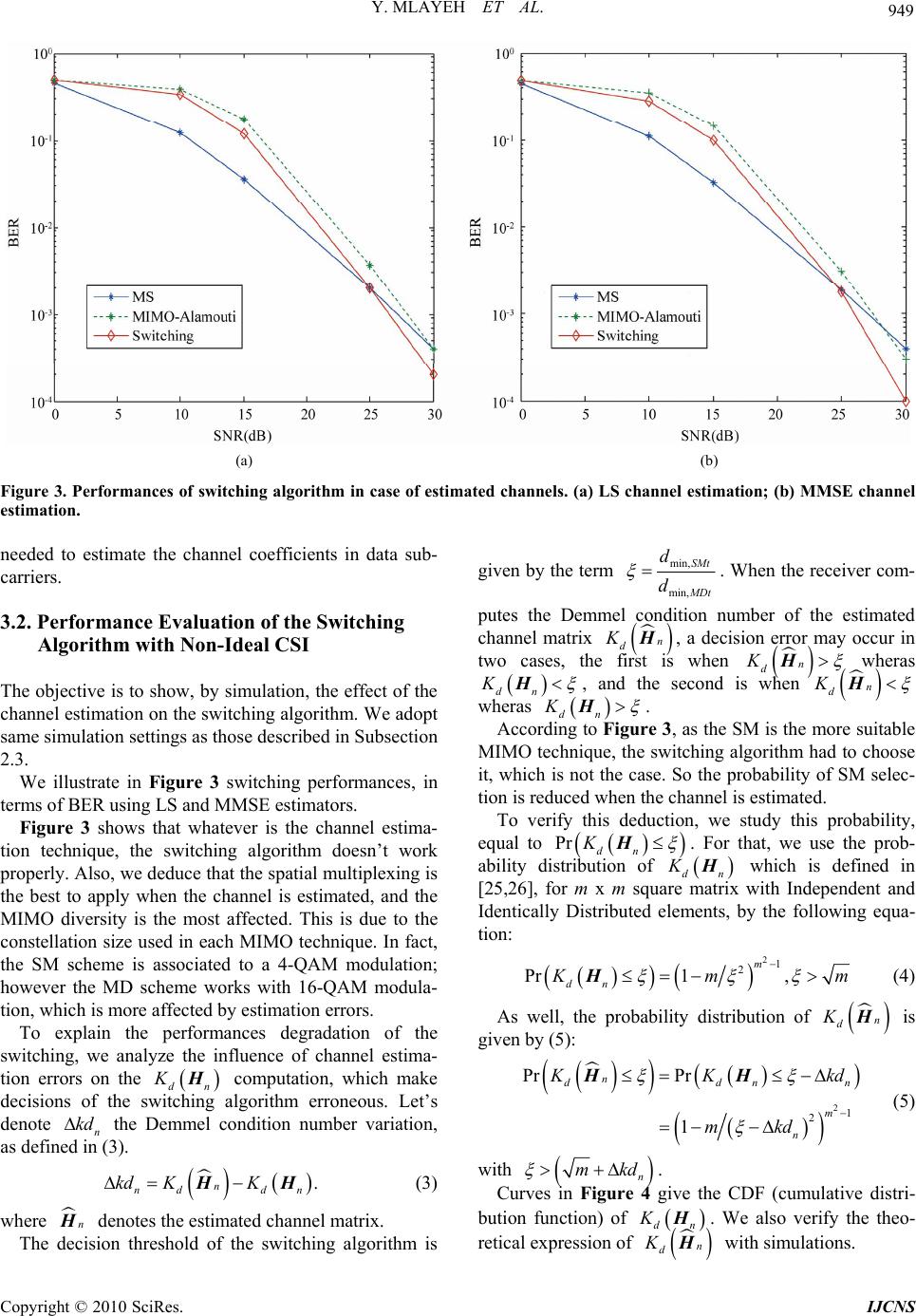

Y. MLAYEH ET AL.
949
(a) (b)
Figure 3. Performances of switching algorithm in case of estimated channels. (a) LS channel estimation; (b) MMSE channel
estimation.
needed to estimate the channel coefficients in data sub-
carriers. given by the term min,
min,
SMt
M
Dt
d
d
 . When the receiver com-
putes the Demmel condition number of the estimated
channel matrix



n
d
K
H
, a decision error may occur in
two cases, the first is when


n
d
K

H wheras


dn
K


H, and the second is when



n
d
K


H
wheras


3.2. Performance Evaluation of the Switching
Algorithm with Non-Ideal CSI
The objective is to show, by simulation, the effect of the
channel estimation on the switching algorithm. We adopt
same simulation settings as those described in Subsection
2.3.
dn
K

H.
According to Figure 3, as the SM is the more suitable
MIMO technique, the switching algorithm had to choose
it, which is not the case. So the probability of SM selec-
tion is reduced when the channel is estimated.
We illustrate in Figure 3 switching performances, in
terms of BER using LS and MMSE estimators. To verify this deduction, we study this probability,
equal to




Pr dn K


HK. For that, we use the prob-
ability distribution of

dn
Figure 3 shows that whatever is the channel estima-
tion technique, the switching algorithm doesn’t work
properly. Also, we deduce that the spatial multiplexing is
the best to apply when the channel is estimated, and the
MIMO diversity is the most affected. This is due to the
constellation size used in each MIMO technique. In fact,
the SM scheme is associated to a 4-QAM modulation;
however the MD scheme works with 16-QAM modula-
tion, which is more affected by estimation errors.

H
which is defined in
[25,26], for m x m square matrix with Independent and
Identically Distributed elements, by the following equa-
tion:
 

21
2
Pr1 ,
m
dn
K
mm 

H (4)
As well, the probability distribution of



n
d
K
H
is
given by (5):
To explain the performances degradation of the
switching, we analyze the influence of channel estima-
tion errors on the dn

K

H
computation, which make
decisions of the switching algorithm erroneous. Let’s
denote n the Demmel condition number variation,
as defined in (3).
kd





 


21
2
Pr Pr
1
n
ddn
m
n
n
K
Kk
mkd



 
 
HHd
(5)
with


n
mkd  .



.
n
nd dn
kd KK HH (3) Curves in Figure 4 give the CDF (cumulative distri-
bution function) of


dn
K
H
. We also verify the theo-
retical expression of



n
d
K
H
with simulations.
where

n
H
denotes the estimated channel matrix.
The decision threshold of the switching algorithm is

950 Y. MLAYEH ET AL.
Figure 4. CDF of in cases of ideal and non ideal CSI.
d
K
As mentioned above, the probability of choosing the
SM technique decreases, and makes decision errors oc-
curs when applying the switching algorithm.
Also, when analyzing the Expression (5), we deduce
that the Demmel condition number variation


n
kd
could be expressed by a shift in the decision threshold
. Hence, one idea consists of using an “opti-
mal threshold” to offset the effect of channel estimation
on the decision metric. This is the topic of the next sub-
section.

n
kd  

3.3. Analysis of Erroneous Switching
Decision-Optimal Threshold Technique
Description
The objective is to settle, for each estimator NMSE
(Normalized Mean Square Error) value, an optimal
threshold opt

that minimizes the switching decision
errors by compensating n. The MSE is defined in
(6), for
kd
s
N channel realizations.

2
2
1
1sk
k
N
k
sk
NMSE N

HH
H (6)
for that, we apply the switching algorithm to estimate
channels with different NMSE values, and we determine,
for each of them, the optimal threshold value that allows
the same switching decision as the one deduced in the
case of a perfect channel knowledge. The
s
N value is
chosen equal to 800, for which a further increase holds
negligible impact on opt

. We illustrate in Figure 5 re-
sulted optimal thresholds as functions of NMSE.
The curve of Figure 5 shows that opt

increases with
NMSE, which means that probability of SM selection
should increase as much as the estimation error is im-
portant. This agrees with results in Figure 4 where we
show that the variation n kd

take positive values and
according to (5), the SM selection probability decrease as
the n
kd

increase.
Basing on several previous works that are interested to
study the relation between SNR and MSE in estimated
channels [27], the optimal threshold technique is sum-
marized according to the following steps:
1) Fix the SNR value which is considered as a metric
of Channel State Information.
2) Determine, from the SNR value and its correspon-
ding MSE, opt

value that will be used in the switching
algorithm.
3) Apply the switching algorithm, using opt

, to choose
the appropriate MIMO technique.
To validate this extra-processing, percentages of
switching decision errors, when using

are compared
to those when using opt

. As shown in curves of Figure 6,
Figure 5. Optimal threshold fixing for different values of
NMSE.
Figure 6. Percentage of erroneous decisions—Comparison
between using

and opt

.

Y. MLAYEH ET AL.
951
using optimal threshold improve considerably the switch-
ing decision.
To study the impact of the decision on performances
of switching module in terms of BER, we evaluate per-
formances of switching algorithm with threshold adapta-
tion compared to those using fixed threshold.
The curves of Figure 7 show that the amelioration
added by adaptation process is poor and the switching
technique performances are no longer degraded com-
pared to Spatial Multiplexing. So, we conclude that
channel estimation errors will not create decision errors
only and that the switching algorithm degradation is also
due to the effect of these estimation errors on two MIMO
modes at the time of equalization. This is due to the de-
pendence of channel estimation error on M-QAM con-
stellation in Rayleigh fading channels [28,29]. In fact,
estimation errors are as more important as the constella-
tion is greater. The modulation order used for every
technique (4-QAM and 16-QAM) exhibits an error floor
for low values of SNR (< 25 dB) and this has an impact
on performances of switching algorithm. The blue curves
show that in SNR range [0-25], the SM technique gives
better performances than switching algorithm. Neverthe-
less, for high values of SNR, The switching algorithm
works properly. Hence, developing a robust channel es-
timation method is essential to exploit performances of-
fered by the advanced MIMO algorithms as the switch-
ing algorithm.
3.4. Proposal Solutions to Improve the Switching
Algorithm with Non-Ideal CSI
In this subsection, we describe two solutions to reduce
Figure 7. Performances of the switching algorithm using
opt

in case of estimated channels.
estimation errors in order to improve the switching algo-
rithm performances even in low SNR. The first technique
is to develop a robust method of channel estimation; the
second is to use a reduced constellation in the estimation
by describing a novel channel estimation process.
3.4.1. Robus t Channel Estimati on
In [30], we have developed an IFFT/FFT LS estimation
channel method based only on the knowledge of the
power delay profile of the channel. It consists of adding
an extra IFFT/FFT processing to better estimate channel
coefficients. This method is summarized according to the
following steps [30]:
 Apply the conventional LS estimator to determine
a first approximation of channel frequency re-
sponse coefficients.
 Convert LS estimated coefficients into the time
domain, using the IFFT transform. The result of
this step is impulse response coefficients ˆn h for n =
0,, (N – 1) where N is the subcarrier number.
 Exploit the information providing by the path delay
which is the number L and positions of taps. So,
corresponding impulse response coefficients are
kept, the remaining (N – L) non considered coeffi-
cients will be set to zero. This is conveyed by (6).

01 1
ˆif in,,,
0else
nL
nhnlll
h








(7)
where


01 1
,, ,
L
ll l

 is the set of taps index.
 Apply the FFT transform to the new impulse re-
sponse h
 to obtain frequency response coeffi-
cients n
H
 for 0,1, ,1nN

.
3.4.2. New Switching Process
In Subsection 3.3, we’ve shown that the switching algo-
rithm performances degrade because of different con-
stellation size used by the two MIMO modes. So, the
idea of this part of the work consists of using a small
constellation size to improve the channel estimation and
so the switching algorithm.
For that, we propose to apply a training process based
on the transmission of two OFDM symbols, during one
OFDM symbol period, using the 4-QAM modulation
with SM as a MIMO scheme. By assuming that the
channel is constant over three OFDM symbol periods,
the information provided after this training period is ex-
ploited to:
 Compute the Demmel condition number to have
knowledge about the “goodness” of every subcar-
rier for use in SM or MD. The decision vector will
be applied to do the switching in the next two
OFDM symbol periods.
 Apply the estimated channel coefficients in equa-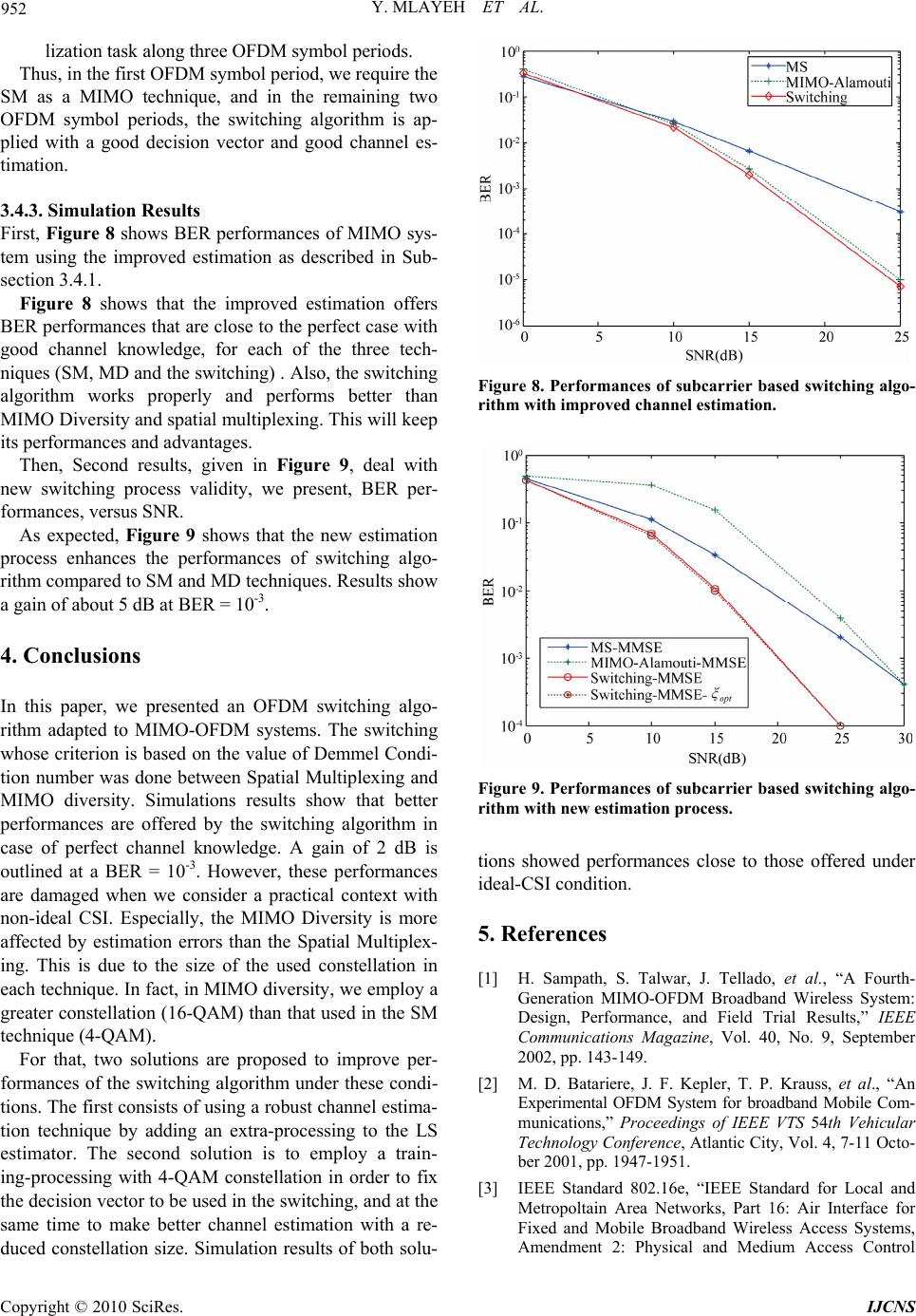

952 Y. MLAYEH ET AL.
lization task along three OFDM symbol periods.
Thus, in the first OFDM symbol period, we require the
SM as a MIMO technique, and in the remaining two
OFDM symbol periods, the switching algorithm is ap-
plied with a good decision vector and good channel es-
timation.
3.4.3. Simulation Results
First, Figure 8 shows BER performances of MIMO sys-
tem using the improved estimation as described in Sub-
section 3.4.1.
Figure 8 shows that the improved estimation offers
BER performances that are close to the perfect case with
good channel knowledge, for each of the three tech-
niques (SM, MD and the switching) . Also, the switching
algorithm works properly and performs better than
MIMO Diversity and spatial multiplexing. This will keep
its performances and advantages.
Then, Second results, given in Figure 9, deal with
new switching process validity, we present, BER per-
formances, versus SNR.
As expected, Figure 9 shows that the new estimation
process enhances the performances of switching algo-
rithm compared to SM and MD techniques. Results show
a gain of about 5 dB at BER = 10-3.
4. Conclusions
In this paper, we presented an OFDM switching algo-
rithm adapted to MIMO-OFDM systems. The switching
whose criterion is based on the value of Demmel Condi-
tion number was done between Spatial Multiplexing and
MIMO diversity. Simulations results show that better
performances are offered by the switching algorithm in
case of perfect channel knowledge. A gain of 2 dB is
outlined at a BER = 10-3. However, these performances
are damaged when we consider a practical context with
non-ideal CSI. Especially, the MIMO Diversity is more
affected by estimation errors than the Spatial Multiplex-
ing. This is due to the size of the used constellation in
each technique. In fact, in MIMO diversity, we employ a
greater constellation (16-QAM) than that used in the SM
technique (4-QAM).
For that, two solutions are proposed to improve per-
formances of the switching algorithm under these condi-
tions. The first consists of using a robust channel estima-
tion technique by adding an extra-processing to the LS
estimator. The second solution is to employ a train-
ing-processing with 4-QAM constellation in order to fix
the decision vector to be used in the switching, and at the
same time to make better channel estimation with a re-
duced constellation size. Simulation results of both solu-
Figure 8. Performances of subcarrier based switching algo-
rithm with improved channel estimation.
Figure 9. Performances of subcarrier based switching algo-
rithm with new estimation process.
tions showed performances close to those offered under
ideal-CSI condition.
5. References
[1] H. Sampath, S. Talwar, J. Tellado, et al., “A Fourth-
Generation MIMO-OFDM Broadband Wireless System:
Design, Performance, and Field Trial Results,” IEEE
Communications Magazine, Vol. 40, No. 9, September
2002, pp. 143-149.
[2] M. D. Batariere, J. F. Kepler, T. P. Krauss, et al., “An
Experimental OFDM System for broadband Mobile Com-
munications,” Proceedings of IEEE VTS 54th Vehicular
Technology Conference, Atlantic City, Vol. 4, 7-11 Octo-
ber 2001, pp. 1947-1951.
[3] IEEE Standard 802.16e, “IEEE Standard for Local and
Metropoltain Area Networks, Part 16: Air Interface for
Fixed and Mobile Broadband Wireless Access Systems,
Amendment 2: Physical and Medium Access Control

Y. MLAYEH ET AL.
953
Layers for Combined Fixed and Mobile Operation in
Licensed Bands and Corrigendum 1,” February 2006.
[4] D. Gesbert, M. Shafi, D. Shiu, P. J. Smith and A. Naguib,
“From Theory to Practice: An Overview of MIMO Space
Time Coded Wireless Systems,” IEEE Journal on Se-
lected Areas in Communications, Vol. 21, No. 3, April
2003, pp. 281-302.
[5] S. M. Alamouti, “A Simple Transmit Diversity Technique
for Wireless Communications,” IEEE Journal on Selec-
ted Areas in Communications, Vol. 16, No. 8, October
1998, pp. 1451-1458.
[6] V. Tarokh, H. Jafarkhani and A. R. Calderbank, “Space
Time Block Codes from Orthogonal Designs,” IEEE
Transactions on Information Theory, Vol. 45, No. 5, July
1999, pp. 1456-1467.
[7] A. J. Paulraj and T. Kailath, “Increasing Capacity in Wire-
less Broadcast Systems Using Distributed Transmission/
Directional Reception (DTDR),” U. S. Patent 5,345,599,
September 1994.
[8] J. Adeane, W. Q. Malik and I. J. Wassell, “Error Perfor-
mance of Ultrawideband Spatial Multiplexing Systems,”
IET Microwaves, Antennas & Propagation, Vol. 3, No. 3,
March 2009, pp. 363-371.
[9] R. W. Heath Jr. and A. J. Paulraj, “Switching between
Diversity and Multiplexing in MIMO Systems,” IEEE
Transactions on Communications, Vol. 53, No. 6, June
2005, pp. 962-968.
[10] R. W. Heath Jr. and A. J. Paulraj, “Diversity versus
Multiplexing in Narrowband MIMO Channels: A Tradeoff
Based on Euclidean Distance,” IEEE Transactions on
Communications, December 2002, pp. 1-26.
[11] R. W. Heath Jr. and A. J. Paulraj, “Characterization of
MIMO channels for Spatial Multiplexing Systems,” Pro-
ceedings of IEEE International Conference on Communi-
cations, Helsinki, Vol. 2, 11-14 June 2001, pp. 591-595.
[12] N. Kita, W. Yamada, A. Sato, D. Mori and S. Uwano,
“Measurement of Demmel Condition Number for 2 × 2
MIMO-OFDM Broadband Channels,” Proceedings of IEEE
59th Vehicular Technology Conference, Milan, Vol. 1,
17-19 May 2004, pp. 294-298.
[13] C. Han, A. Doufexi, S. Armour, K. H. Ng and J. McGeehan,
“Adaptive MIMO OFDMA for Future Generation Cellular
Systems in Realistic Outdoor Environment,” Proceedings
of IEEE 63rd Vehicular Technology Conference, Mel-
bourne, 7-10 May 2006, pp. 142-146.
[14] C. Han, S. Armour, A. Doufexi, K. H. Ng and J. McGeehan,
“Link Adaptation Performance Evaluation for a MIMO-
OFDM Physical Layer in a Realistic Outdoor Environment,”
Proceedings of IEEE 64th Vehicular Technology Confer-
ence, Montreal, Vol. 74, 25-28 September 2006, pp. 1-5.
[15] B. Muquet, E. Biglieri and H. Sari, “MIMO Link Adap-
tation in Mobile WiMAX Systems,” Proceedings of IEEE
Wireless Communications and Networking Conference,
Kowloon, 11-15 March 2007, pp. 1810-1813.
[16] A. Forenza, M. R. McKay, I. B. Collings and R. W.
Heath Jr., “Switching bewteen OSTBC and Spatial Multi-
plexing with Linear Receivers in Spatially Correlated
MIMO Channels,” Proceedings of IEEE 63rd Vehicular
Technology Conference, Melbourne, Vol. 3, 7-10 May
2006, pp. 1387-1391.
[17] A. Forenza, M. R. McKay, A. Pandharipande, R. W. Heath
Jr. and I. B. Collings, “Adaptive MIMO Transmission for
Exploiting the Capacity of Spatially Correlated Channels,”
IEEE Transactions on Vehicular Technology, Vol. 56, No.
2, March 2007, pp. 619-630.
[18] C. Wood and W. S. Hodgkiss, “MIMO Channel Models
and Performance Metrics,” Proceedings of IEEE Global
Telecommunications Conference, Washington DC, 26-30
November 2007, pp. 3740-3744.
[19] J. W. Demmel, “The Probability that a Numerical Analysis
Problem is Difficult,” Mathematics of Computation, Vol.
50, No. 182, 1988, pp. 449-480.
[20] D. Chen, I.-K. Fu, M. Hart and W. C. Wong, “Project
IEEE 802.16j Relay Task Group; Channel Models and
Performance Metrics for IEEE 802.16j Relay Task
Group,” IEEE 802.16j MMR Contribution, May 2006.
[21] W. C. Wong, I.-K. Fu, D. Chen, M. Hart and P. Wang,
“Comparison of Multipath Channel Models for IEEE
802.16j Relay Task Group,” 01-07-2006.
[22] Y. S. Shen and E. Martinez, “WiMAX Channel Estimation:
Algorithms and Implementations,” Freescale Semiconductor,
Application Note, Revision 0, Draft A, July 2007.
[23] M. Hsieh and C. Wei, “Channel Estimation for OFDM
Systems Based on Comb-Type Pilot Arrangement in
Frequency Selective Fading Channels,” IEEE Transactions
on Consumer Electron ics, Vol. 44, No. 1, 1998, pp. 217-225.
[24] Y. S. Shen and E. Martinez, “Channel Estimation in OFDM
Systems,” Freescale Semiconductor, Applic ation Note, Re-
vision 0, January 2006.
[25] A. Edelman, “On the Distribution of a Scaled Condition
Number,” Mathematics of Computation, Vol. 58, No. 197,
1992, pp. 185-190.
[26] T. Tao and Van Vu, “The Condition Number of a Ran-
domly Perturbed Matrix,” Proceedings of the 39th Annual
ACM Symposium on Theory of Computing, San Diego,
11-13 June 2007, pp. 248-255.
[27] E. K. Hlel, F. Tlili, S. Cherif and M. Siala, “Channel
Parameters Estimation for OFDM Systems,” International
Symposium on Communications, Control and Signal Pro-
cessing, Marrakech, 13-15 March 2006, pp. 1-4.
[28] X. Y. Tang, M.-S. Alouini and A. J. Goldsmith, “Effect
of Channel Estimation Error on M-QAM BER Perfor-
mance in Rayleigh Fading,” IEEE Transactions on Com-
munications, Vol. 47, No. 12, 1999, pp. 1856-1864.
[29] L. Z. Cao and N. C. Beaulieu, “Exact Error-Rate Analysis
of Diversity 16-QAM with Channel Estimation Error,”
IEEE Transactions on Communications, Vol. 52, No. 6,
June 2004, pp. 1019-1029.
[30] Y. Mlayeh, F. Rouissi, F. Tlili and A. Ghazel, “Improve-
ment Technique of Channel Estimation in OFDM-MIMO
Systems,” Proceedings of 16th IEEE International Con-
ference on Electronics, Circuits and Systems, Hammamet,
13-16 December 2009, pp. 467-470.