Circuits and Systems, 2013, 4, 276-279
http://dx.doi.org/10.4236/cs.2013.43037 Published Online July 2013 (http://www.scirp.org/journal/cs)
Logic Picture-Based Dynamic Power Estimation for Unit
Gate-Delay Model CMOS Circuits
Omnia S. Ahmed1, Mohamed F. Abu-Elyazeed1, Mohamed B. Abdelhalim2,
Hassanein H. Amer3*, Ahmed H. Madian4
1Faculty of Engineering, Cairo University, Giza, Egypt
2College of Computing and Information Technology, Arab Academy for Science, Technolog y & Maritime Transport, Cairo, Egypt
3Electronics Engineering Department, American University in Cairo, Cairo, Egypt
4Radiation Engineering Department, Egyptian Atomic Energy Authority, Cairo, Egypt
Received February 1, 2013; revised March 1, 2013; accepted March 9, 2013
Copyright © 2013 Omnia S. Ahmed et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
In this research, a fast methodology to calculate the exact value of the average dynamic power consumption for CMOS
combinational logic circuits is developed. The delay model used is the unit-delay model where all gates have the same
propagation delay. The main advantages of this method over other techniques are its accuracy, as it is deterministic and
it requires less computational effort compared to exhaustive simulation approaches. The methodology uses the Logic
Pictures concept for obtaining the nodes’ toggle rates. The proposed method is applied to well-known circuits and the
results are compared to exhaustive simulation and Monte Carlo simulation methods.
Keywords: Dynamic Power Estimation; Logic Pictures; CMOS Digital Logic Circuits; Toggle Rate; Unit-Delay Model
1. Introduction
Power dissipation is an important parameter for digital
VLSI circuits as the excessive power consumption may
lead to runtime errors or permanent damages due to
overheating. Hence, along with low power design tech-
niques at different levels of the design, accurate power
estimation tools are highly needed. Currently, there are
many methods for estimating the power consumption;
they are mainly categorized as non simulative-based [1-5]
and simulative-based methods [6-9]. Non simulative-
based methods can either be probabilistic or statistical.
They rely on probabilistic measures for the inputs and the
switching activities to estimate the power. While being
efficient for large circuits with acceptable margins of
errors, the power produced is not accurate but only an
estimate. For simulative-based methods, the circuit is
simulated with different inputs to obtain the power con-
sumption. The main problems in simulative-based meth-
ods are the large memory requirements, time consump-
tion and how to find the representative input vector set
needed to exercise the circuit. Exhaustive simulations
(where all pairs of input vectors are applied to the circuit)
are very accurate but, obviously, time consuming, espe-
cially for large circuits.
In [10], an accurate method was introduced for calcu-
lating the average and the maximum dynamic power at
the gate level. The paper developed the concept of Logic
Pictures (LPs) in calculating the average power. As the
LP is the status of gates outputs, it was found that the
number of LPs was much smaller than the number of
inputs patterns; hence, LPs were used instead of input
patterns to obtain all the possible transitions for circuit
nodes then obtaining the power consumption. The main
advantage of this method is that it is deterministic and
the simulations required are much less time-consuming
than exhaustive simulations. The logic picture concept
was modified in [11] to calculate the average power con-
sumption for sequential circuits. In [12], the method was
generalized and extended to calculate the maximum
power consumption for sequential circuits including all
types of Flip-Flops and their internal nodes power con-
sumption; it was also shown how the tool could be used
for design space exploration to select the appropriate
Flip-Flop that consumed less power. While the method in
[10-12] is accurate, it assumed that no propagation delay
was associated with logic gates, i.e., zero-delay model.
In this research, a method to calculate an accurate tog-
gle rate assuming unit-delay model, is presented using
*Corresponding a uthor.
C
opyright © 2013 SciRes. CS

O. S. AHMED ET AL. 277
the LP concept. Th e toggle rate can be directly related to
the dynamic power consumption. The proposed method
is backward-compatible as it can be easily modified to ob-
tain the power consumption for the zero-delay gate model.
The rest of this paper is organized as follows. Section
2 introduces the methodology to calculate the switching
activity of the circuit nodes under unit-delay model as-
sumption for all the gates. Section 3 contains the experi-
mental results while Section 4 has the conclusions.
2. Methodology
For CMOS logic circuits, the average dynamic power can
be calculated as follo ws [13]:
2
ddclki i
N
f c
1
2
avg
PV


V
(1)
where dd is the supply voltage, clk
f
is the clock fre-
quency, N is the number of gates ou tputs (circuit nodes),
αi is the toggle rate of the output of gate i and ci is the
output capacitance of gate i. From this equation, it can be
seen that dd
V and clk
f
depend on the fabrication
technology while ci is linearly proportional to the gate
fan-out; the only parameter that depends on the circuit
operation is αi. Therefore , th e tog g le rate of the nodes is a
good indicator of power dissipation [14].
Consider the circuit in Figure 1 and assume that all
inputs have equal probabilities to be 0 or 1.
The circuit has 2 gate outputs (nodes): d and e. As
shown in the truth table in Table 1, column 3 indicates
that the circuit has 3 LPs for the output nodes: 00, 01 and
11. Each LP is associated with a Logic Group (LG)
composed of the input vectors that leads to this picture.
For LP1, LG1 contains 3 input vectors that lead to LP1:
000, 010 and 100. Hence, 1 LG 3. Similarly,
2
LG 3 and 3 LG 2.
Now, if the unit-delay model is assumed, a propaga-
tion delay δ is assigned for each gate and Table 2 can be
easily constructed.
Starting from an initial LP at time t = 0, if the input
vector is from the LG that leads to the same initial LP,
then it is not considered as there is no transition and
hence no power consumption, while all the input vectors
that belong to other LGs must be applied to get different
LPs. The status of the nodes temporarily changes into
other transient LPs at t = δ and finally change into a third,
and final, LP at t = 2δ since there are 2 gates in the criti-
cal path. The transient LPs and the final LP are merged
into one LP in the rightmost column of Table 2.
Figure 1. A simple 3-input circuit.
Table 1. Circuit logic pictures with zero-delay model.
Inputs Outputs
a b c d e
Logic
pictures Logic groups
0 0 0 0 0 LP1 = “00” LG1
0 0 1 0 1 LP2 = “01” LG2
0 1 0 0 0 LP1 LG1
0 1 1 0 1 LP2 LG2
1 0 0 0 0 LP1 LG1
1 0 1 0 1 LP2 LG2
1 1 0 1 1 LP3 = “11” LG3
1 1 1 1 1 LP3 LG3
The number of transitions between the initial LPs and
the merged LPs is calculated in Table 3. As an example,
the transition between LP1,0 and LP1 can be obtained as
follows: from Table 1, th e numb er of inpu ts th at lead s to
LP1,0 is 3 (remember that 1) while from Table
2, LP1 appeared after LP1,0 for 3 different inputs; hence,
the number of different combinations of inputs that could
lead from LP1,0 to LP1 is 3 × 3 = 9. LP2 and LP3 appeared
only once in Table 2 after LP1,0; hence, the number of
different input combinations that leads to LP2 and LP3 is
1 × 3 = 3. Finally, there is no input that leads from LP1,0
to LP4 or LP5 which means zero direct transition between
them.
LG 3


To obtain the node transitions, if a node in the logic
picture toggles from 1 to 0 or 0 to 1, then it is considered
as a toggle. Then, this togg le is multiplied by the nu mber
of all possible input vectors that lead to this toggle. The
same is done for all LPs through time. The possible
number for transition for each node is then accumulated
and divided by 22n to obtain the toggle rate. Fo r example,
LP3,0 is “11”; the logic picture changes to LP1,δ which is
“01”. This means that node d toggles from 1 to 0. All
possible input transitions from LP3,0 to LP1,δ can be ob-
tained from Table 3 as LP1,δ is a part of LP1 and LP5,
then the input transitions are 6 + 6 = 12. In addition,
there are toggles at node d from LP1,0 to LP2,δ, LP1,0 to
LP3,δ, LP2,0 to LP2,δ and LP2,0 to LP3,δ with 3 possible
input transitions for all 4 transitions cases. This leads to
12 other possible transitions. Hence, for node d, the
number of transitions is 24. The same can be done with
node e resulting into 36 transitions.
To conclude, the following equation can be used to
obtain the toggle rate αi with the unit-delay model:
12
,
11 12
,
2
ktk t
s
lm tlm
tl m
in
RtrPP



 
  (2)
where s is the number of stages in the critical path, K1
and K2 are the LPs in each state where the two states
ust be consecutive with respect to gates delay, i.e., a m

O. S. AHMED ET AL. 278
Table 2. All possible logic pictures for the unit-delay model.
Applied InLP t = 2δ puts Initial LP t = 0 Transient LP t = δFinal
Logic Group Merged LP
a b c d e d e d e
LG2 “LP1,0” P1,δ” “LP1,2δ” 0 1 0 1 “LP1”0 0 1 0 0 0 1 “L0 1
LG2 0 1 1 0 0 “LP1,0” 0 1 “LP1,δ” 0 1 “LP1,2δ” 0 1 0 1 “LP1”
LG2 1 0 1 0 0 “LP1,0” 0 1 “LP1,δ” 0 1 “LP1,2δ” 0 1 0 1 “LP1”
LG3 1 1 0 0 0 “LP1,0” 1 0 “LP2,δ”
1 1 “LP2,2δ” 1 0 1 1 “LP2”
LG3 1 1 1 0 0 ’LP1,0’ 1 1 “LP3,δ” 1 1 “LP2,2δ” 1 1 1 1 “LP3”
LG1 0 0 0 0 1 “LP2,0” 0 0 “LP4,δ” 0 0 “LP3,2δ” 0 0 0 0 “LP4”
LG1 0 1 0 0 1 “LP2,0” 0 0 “LP4,δ” 0 0 “LP3,2δ” 0 0 0 0 “LP4”
LG1 1 0 0 0 1 “LP2,0” 0 0 “LP4,δ” 0 0 “LP3,2δ” 0 0 0 0 “LP4”
LG3 1 1 0 0 1 “LP2,0” 1 0 “LP2,δ” 1 1 “LP2,2δ” 1 0 1 1 “LP2”
LG3 1 1 1 0 1 “LP2,0” 1 1 “LP3,δ” 1 1 ’LP2,2δ” 1 1 1 1 “LP3”
LG1 0 0 0 1 1 “LP3,0” 0 1 “LP1,δ” 0 0 “LP3,2δ” 0 1 0 0 “LP5”
LG1 0 1 0 1 1 “LP3,0” 0 1 “LP1,δ” 0 0 “LP3,2δ” 0 1 0 0 “LP5”
LG1 1 0 0 1 1 “LP3,0” 0 1 “LP1,δ” 0 0 “LP3,2δ” 0 1 0 0 “LP5”
LG2 0 0 1 1 1 “LP3,0” 0 1 “LP1,δ” 0 1 “LP1,2δ” 0 1 0 1 “LP1”
LG2 0 1 1 1 1 “LP3,0” 0 1 “LP1,δ” 0 1 “LP1,2δ” 0 1 0 1 “LP1”
LG2 1 0 1 1 1 “LP3,0” 0 1 “LP1,δ” 0 1 “LP1,2δ” 0 1 0 1 “LP1”
ate at δ and the other state at 2δ. Rl,m are the repetition st
of the LPs pl and pm within a state and

,1

lm
tr pp if
there is a node transition between pl and s 0
otherwise.
3. Experimental Results
pm and equal
Figure 2. It was
(with size of 2n), the tool running time is less than the
lation approach.
The circuit used in [10] is shown in
studied with the unit-delay mo del and it was noticed that
the number of nodes transitions increased (compared to
the zero-delay model) du e to the glitch es arising from the
gates delays as shown in Table 4 .
To validate the results of the proposed method, ex-
haustive and Monte Carlo simulations (as in [8]) are ap-
plied to the ISCAS-85 C17 benchmark circuit, the 7483
4-bit binary adder and the 74157 Quad 2-input multi-
plexer. The characteristics of these circuits are shown in
Table 5. The resulting power is compared to that ob-
tained using the proposed method. It is found that the
difference between the obtained results from the pro-
posed method and the Monte Carlo approach is negligi-
ble. Moreover, the results obtained are identical to those
obtained usi ng exhaustive simulat i ons.
Since the simulation requires building the truth table
time required for the exhaustive simu
The memory saving ratio can be calculated as the ratio
between the memory space required to store the LPs and
the memory space needed for the exhaustive simulations
[10]. For exhaustive simulations,


2212



nn vec-
tors must be stored; each vector represents a circuit input
transition and consists of all the possible values for all
circuit nodes; hence its size, in bit num-
ber of circuit nodes times the number of LPs. In the
methodology proposed in this research, only 2
s, is equal to the

n


1

K vectors are required where k is the number of
LGs. The size of each vector is identical to that men-
tioned in the exhaustive simulation method.
ly the proposed method could be used to obtain
the power consumption for the zero-delay model consid-
ering only the initial and final states; the power con-
su
Final
d accurate method
to calculate the node toggle rate, hence dynamic power
mption obtained is found to be identical to the one
calculated using the techn ique in [10].
4. Conclusion
This paper discussed a deterministic an

O. S. AHMED ET AL. 279
Table 3. All transitions between initial LPs and merged
LPs.
LP1,0 LP2,0 LP3,0
LP1 9 0 6
LP2 3 3 0
L3 P3 3 0
LP4 0 9 0
LP5 0 0 6
Ta. Node trans with dit delay m
Nonsitions E
G H
ble 4sitionfferenodels.
de tra
F
Zero-delay model 96 120 110 126
Unit-delay model 96 144 152 144
Tesit chterist
Circuit Inputs
Nodes L
count
Crit
path Me
saving
Table 5.t circuaracics.
Ps ical
gates
mory
ISCAS85-C17 5 6 10 1.7 3
7483 9 36 162 4 1.6
74157 10 15 34 4 15.5
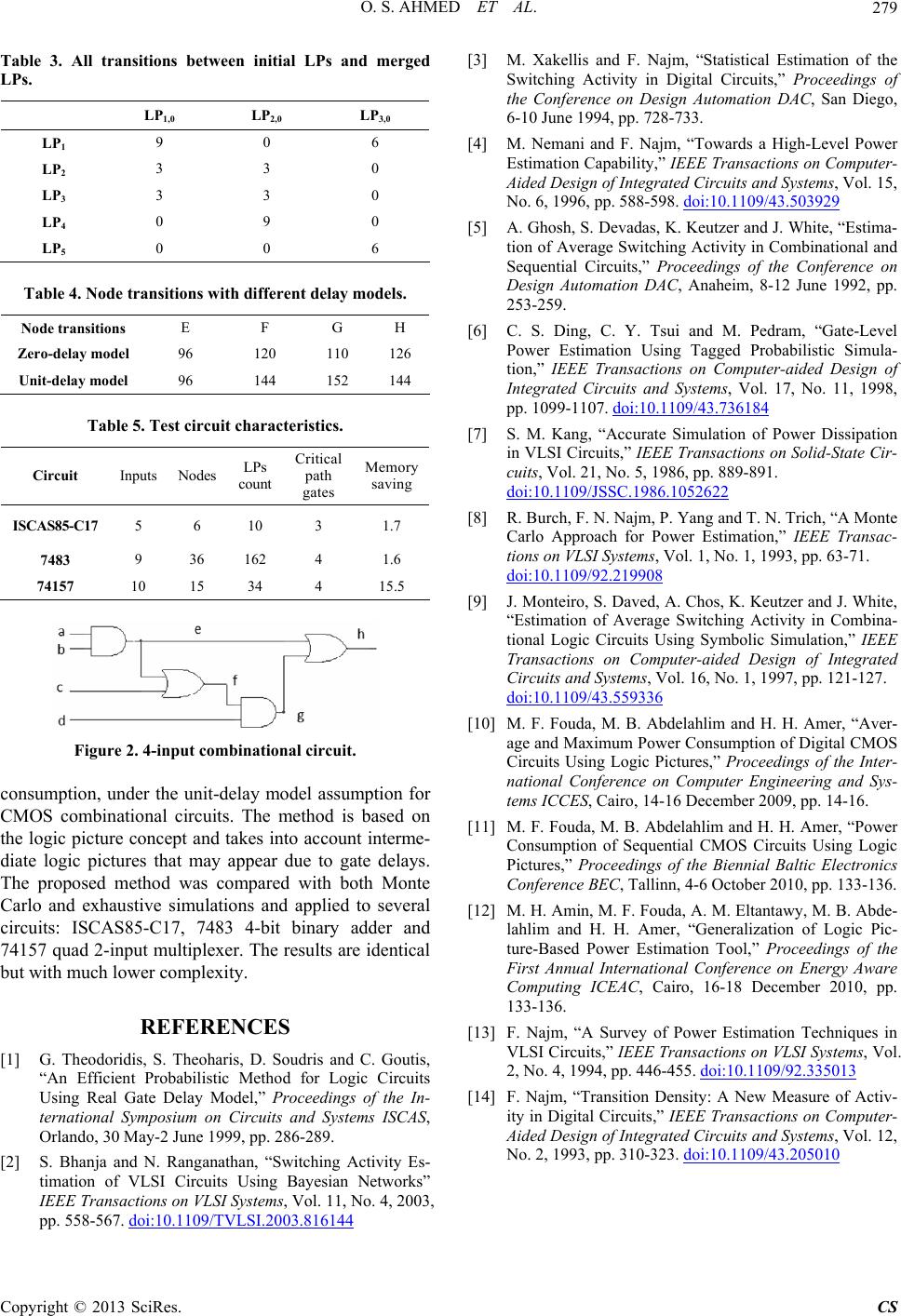
Figure 2. 4-input combinational circuit.
consumption, under the unit-delay model assump
CMOS coba
e logic interme-
. Soudris and C. Goutis,
“An Efficient Probabilistic Method for Logic Circuits
Using Real Geedings of the In-
ternational Syd Systems ISCAS
4
tion f
sed on
or
mbinational circuits. The method is
picture concept and takes into account th
diate logic pictures that may appear due to gate delays.
The proposed method was compared with both Monte
Carlo and exhaustive simulations and applied to several
circuits: ISCAS85-C17, 7483 4-bit binary adder and
74157 quad 2-inpu t multiplexer. Th e results are identical
but with much lower complexity.
REFERENCES
[1] G. Theodoridis, S. Theoharis, D
ate Delay Model,” Proc
mposium on Circuits an,
Orlando, 30 May-2 June 1999, pp. 286-289.
[2] S. Bhanja and N. Ranganathan, “Switching Activity Es-
timation of VLSI Circuits Using Bayesian Networks”
IEEE Transactions on VLSI Systems, Vol. 11, No. 4, 2003,
pp. 558-567. doi:10.1109/TVLSI.2003.81614
an Diego,
cuits and Systems, Vol. 15,
[3] M. Xakellis and F. Najm, “Statistical Estimation of the
Switching Activity in Digital Circuits,” Proceedings of
the Conference on Design Automation DAC, S
6-10 June 1994, pp. 728-733.
[4] M. Nemani and F. Najm, “Towards a High-Level Power
Estimation Capability,” IEEE Transactions on Computer-
Aided Design of Integrated Cir
No. 6, 1996, pp. 588-598. doi:10.1109/43.503929
[5] A. Ghosh, S. Devadas, K. Keutzer and J. White, “Esti ma-
tion of Average Switching Activity in Combinational and
Sequential Circuits,” Proceedings of the Conference on
E Transactions on Computer-aided Design of
Design Automation DAC, Anaheim, 8-12 June 1992, pp.
253-259.
[6] C. S. Ding, C. Y. Tsui and M. Pedram, “Gate-Level
Power Estimation Using Tagged Probabilistic Simula-
tion,” IEE
Integrated Circuits and Systems, Vol. 17, No. 11, 1998,
pp. 1099-1107. doi:10.1109/43.736184
[7] S. M. Kang, “Accurate Simulation of Power Dissipation
in VLSI Circuits,” IEEE Transactions on Solid-State Cir-
cuits, Vol. 21, No. 5, 1986, pp. 889-891.
doi:10.1109/JSSC.1986.1052622
[8] R. Burch, F. N. Najm, P. Yang and T. N. Trich, “A Monte
Carlo Approach for Power Estimation,”
tions on VLSI Systems, Vol. 1, No. IEEE Transac- 1, 1993, pp. 63-71.
doi:10.1109/92.219908
[9] J. Monteiro, S. Daved, A. Chos, K. Keutzer and J. White,
“Estimation of Average Switching Activity in Combin
tional Logic Circuits Usa- ing Symbolic Simulation,” IEEE
Transactions on Computer-aided Design of Integrated
Circuits and Systems, Vol. 16, No. 1, 1997, pp. 121-127.
doi:10.1109/43.559336
[10] M. F. Fouda, M. B. Abdelahlim and H. H. Amer, “Aver-
age and Maximum Power Consumption of Digital CMOS
Circuits Using Logic Pic tures,” Proceedings of the Inter-
ics
994, pp. 446-455. doi:10.1109/92.335013
national Conference on Computer Engineering and Sys-
tems ICCES, Cairo, 14-16 December 2009, pp. 14-16.
[11] M. F. Fouda, M. B. Abdelahlim and H. H. Amer, “Power
Consumption of Sequential CMOS Circuits Using Logic
Pictures,” Proceedings of the Biennial Baltic Electron
Conference BEC, Tallinn, 4-6 October 2010, pp. 133-136.
[12] M. H. Amin, M. F. Fouda, A. M. Eltantawy, M. B. Abde-
lahlim and H. H. Amer, “Generalization of Logic Pic-
ture-Based Power Estimation Tool,” Proceedings of the
First Annual International Conference on Energy Aware
Computing ICEAC, Cairo, 16-18 December 2010, pp.
133-136.
[13] F. Najm, “A Survey of Power Estimation Techniques in
VLSI Circuits,” IEEE Transactions on VLSI Systems, Vol.
2, No. 4, 1
l. 12,
[14] F. Najm, “Transition Density: A New Measure of Activ-
ity in Digital Circuits,” IEEE Transactions on Computer-
Aided Design of Integrated Circuits and Systems, Vo
No. 2, 1993, pp. 310-323. doi:10.1109/43.205010