Int. J. Communications, Network and System Sciences, 2010, 3, 934-942
doi:10.4236/ijcns.2010.312127 Published Online December 2010 (http://www.SciRP.org/journal/ijcns)
Design of NPR-Type Cosine Modulated Filterbank Using
Combinational Window Functions
Ram Kumar Soni1, Alok Jain2, Rajiv Saxena3
1Department of Electronics & Communication Engineering, Samrat Ashok Technological Institute (Polytechnic),
Vidisha, India
2Department of Electronics & Instrumentation Engineering, Samrat Ashok Technological Institute,
Vidisha, India
3Department of Electronics & Communication Engineering, Jaypee University of Engineering & Technology,
Raghogarh, Guna, India
Received September 8, 2010; revised October 10, 2010; accepted November 18, 2010
Abstract
This paper presents the design of near perfect reconstruction (NPR) cosine modulated filterbank (CMFB).
The prototype filter is designed by the combinational window functions. These window functions provide
high side-lobe-fall-off-rate (SLFOR) with better far-end attenuation which suppresses the undesired inter-
ferences occur in the filterbank. A linear optimization is used to minimize the error parameters. Design ex-
amples have been included to illustrate the effectiveness of the proposed technique over the earlier reported
work.
Keywords: Combinational Window Functions, SLFOR, Far-End Attenuation, Stopband Energy
1. Introduction
Cosine modulated filterbank are used in a wide range of
applications, from data compression of speech, audio and
video signals to data transmission [1-6]. They are special
subclass of the general M-channel filterbank, which has
some very attractive features, first, it is a highly selective
and discrimination system. Second, all of the analysis
Hz(z) and synthesis Fz(z) filters of filterbank can be si-
multaneously generated by the cosine modulation of sin-
gle linear phase FIR prototype filter as shown in Fig-
ure 1. Thirdly, the error occurs at the reconstructed out-
put in NPR types system can easily optimized by using
suitable optimization technique [2,7]. The CMFB has
been studied by many prominent authors in PR and NPR
conditions and finds that the NPR type is simple, more
realizable and computationally efficient [3-9]. Also the
performance of the system can be further improved with
high stopband attenuation and narrow transition band-
width of the prototype filter [8].
In speech and audio communication the stopband at-
tenuation (s) of 40-60dB provides the signals of ade-
quate quality if the crosstalk suppression is efficient
[10,11]. It mainly depends on the different parameters of
prototype filter, i.e., stopband energy (Es), far-end at-
tenuation (f) and SLFOR [2,10]. A window function
with minimum stopband energy, better far-end attenua-
tion and high SLFOR is the most suitable in such appli-
cations. Combinational window functions provide all
these characteristics. These are designed by combining a
data window and a lag window function in a linear man-
ner [2,10].
Figure 1. M-band cosine modulated filterbank.

R. K. SONI ET AL.
935
In this proposed work 8-, 16-, 32-band NPR CMFB is
designed. The prototype FIR filter is formulated using
Parzen-Cos6 (PC6) and Papoulis-Cos4 (PC4) combina-
tional window functions [10,12]. The main contribution
of this paper is summarized below:
1) The prototype filter is designed using high SLFOR
combinational window functions.
2) The NPR CMFB is designed using cosine modula-
tion.
3) The reconstructed output is not exact replica of the
input. A linear optimization is applied in order to ap-
proximate the power complementary property.
4) Examples are included to evaluate the performance
of the proposed technique in terms of error parameters,
far-end attenuation and stopband energy.
2. Design of Prototype Filter
The impulse response coefficients of a causal Nth-order
linear phase FIR filter p[n] using window technique is
given by [2]:






pn wnhn (1)
where, h[n] is the impulse response of the ideal lowpass
filter and is expressed as:

 

c
sin 0.5
0.5
nN
hn nN



 (2)
where,


c

is the cutoff frequency of the ideal low-
pass filter.


wn is the used window function. PC6 and
PC4 combinational window functions are used to design
prototype filter. These window functions are character-
ized for high SLFOR and far-end attenuation [10]. The
value of SLFOR for PC4 and PC6 window functions are
–24 dB/octave to –30 dB/octave, –24 dB/octave to –42 dB/
octave, respectively [10,12]. Whereas this figure for
Kaiser window is only –6 dB/octave [2]. The expressions
for these window functions in time domain are given
below [10,12].
2.1. Parzen-Cos6(n
 /N) (PC6) Combinational
Window
The expression for Parzen (lag window, l(n)) and
Cos6(n  /N) (data window, d(n)) combinational window
with 
6 as window shape parameter is given as [10,12]
 
 
666 6
6
6
1,
2
0, 2
where 03.7 and
PC
N
lndn n
wn N
n


  
  







2
63
12412 ,4
21 2,42
nn N
n
NN
ln
nN
n
N

 

 

N






6
6cos, 2
n
dn n
N

 N



 (3)
FIR filter design relationships are given by the fol-
lowing equations [10]:
1) Relationship between window shape parameter (

6)
and desired stopband attenuation (s):



2
6

s
s
ab c 

 (4)
where,
8.15414,0.236709, 0.00218617
for 30.3251.25
s
ab c
 
21.3669,0.605789, 0.00434808
for 51.2568
s
ab c 
 
2) Relationship between normalized window width
parameter (D) and (s):




2
s
s
Da bc

 (5)
where,
1.82892,0.0275481, 0.00157699
for 30.3243.60
s
ab c 
 
1.67702,0.0450205,0
for 43.6049.44
s
ab c

 
 
85.4738,3.41969,0.035784
for 49.4457.48
s
ab c
 
8.60006, 0.477004,0.00355655
for 57.4868.69
s
abc 
 
2.2. Papoulis-Cos4 (n  /N) (PC4) Combinational
Window
The combinational window of Papoulis (lag window, l(n))
and Cos4(n  /N) (data window, d(n)) with 
4 as combina-
tional factor is given by [12]:
  
444 4
4
4
1,
2
0, 2
where 08.235
PC
N
lndn n
wn N
n




 
 







(6)

936 R. K. SONI ET AL.

4
12 2
sin1 2cos,2
nnn
ln n
NNN



 


 
 

N


4
4cos, 2
nN
dn n
N





FIR filter design relationships for PC4 window are
given by the following equation [12].
1) Relationship between window shape parameter (

4)
and desired stopband attenuation (s):








23
4
for 26.1961.08
4
s
ss
s
ab cde   

s
4
(7)
where, a = –69.058755, b = 8.409918, c = –0.321364, d
= 0.005044; e = –0.000028.
2) Relationship between normalized window width
parameter (D) and (s):


23 ,
for 26.1961.08
ss ss
s
Da bcde 
  (8)
where, a = 8.728537, b = –0.412899, c = –0.000713, d =
0.000355; e = –0.000004.
The order (N) of the filter designed by using above
mentioned window functions can be estimated by the
following formula:
1
D
N







(9)
where, D is the window width parameter and



is the
normalized transition width =

2
sp

  with
s

and p

are the stopband and passband frequencies,
respectively.
x


represents the smallest integer greater
than or equal to x.
3. Cosine Modulation
Cosine modulation is one of the efficient techniques
which provide minimum computational cost in the de-
sign of filterbank. All filters of synthesis and analysis
sections are obtained by cosine modulation of a linear
phase lowpass prototype filter [2,13].
 
 
2cos 211
22 4
2cos 211
224
for0 1,and0
k
k
k
k
N
hn pnkn
M
N
fn pnkn
M
kMnN










 









 



 

(10)
where, M is the number of bands and and

k
hn


k
f
n
are the impulse responses of the analysis and synthesis
sections, respectively.
4. Optimization Technique
In NPR system, the PR condition is relaxed by allowing
small amount of errors. There are three types of errors
occur at the reconstructed output, as follows amplitude
(Epp), phase and aliasing (Ea) [2,10]. The measures of
these error parameters are given by the following equa-
tions:


0for
j
Pe M

  (11)





21 2
0
1,
where
j
o
MjkM
j
o
k
Te
Te Pe






 (12)
is the overall distortion transfer function. The accuracy
of first approximation gives aliasing and the accuracy of
the second one gives the reconstruction error. The phase
error is eliminated by linear phase prototype filter.
However, other two distortion parameters can be mini-
mized by applying suitable optimization technique.
Much of work have been done in this field [10,11,14,15].
Initially, Johnston [15] developed a nonlinear optimiza-
tion technique, later on many prominent authors such as
Creusere et al. [11] and Lin et al. [14] and Jain et al. [10]
have simplified it and developed single variable linear
optimization techniques with different objective func-
tions. In the proposed work, a linear gradient optimiza-
tion technique is used with objective function given in
Equation (13). The cutoff frequency of prototype filter is
varied to obtain the minimum value of the objective
function.



2
2
max 1
for 0/
jM
j
Pe Pe
M








(13)
Initially, input parameters, i.e., sampling rate, number
of band, passband and stopband frequencies, passband
ripple and stopband attenuation of prototype filter are
specified and determine the cutoff frequency, transition
band and filter length. Initialize, different optimization
pointers like step size, search direction, flag and initial
(p_err) as well as expected minimum possible values
(e_err) of objective function. Inside the optimization
loop, design the prototype lowpass filter and determine
the bandpass filters for analysis and synthesis sections
using cosine modulation. In optimization routine cutoff
frequency is gradually changed as per the search direc-
tion and calculates the corresponding value of the objec-
tive function. Algorithm halts when it attains the mini-
mum value of the objective function. The flowchart of
optimization is given in appendix section and simulated
on MATLAB 7.0.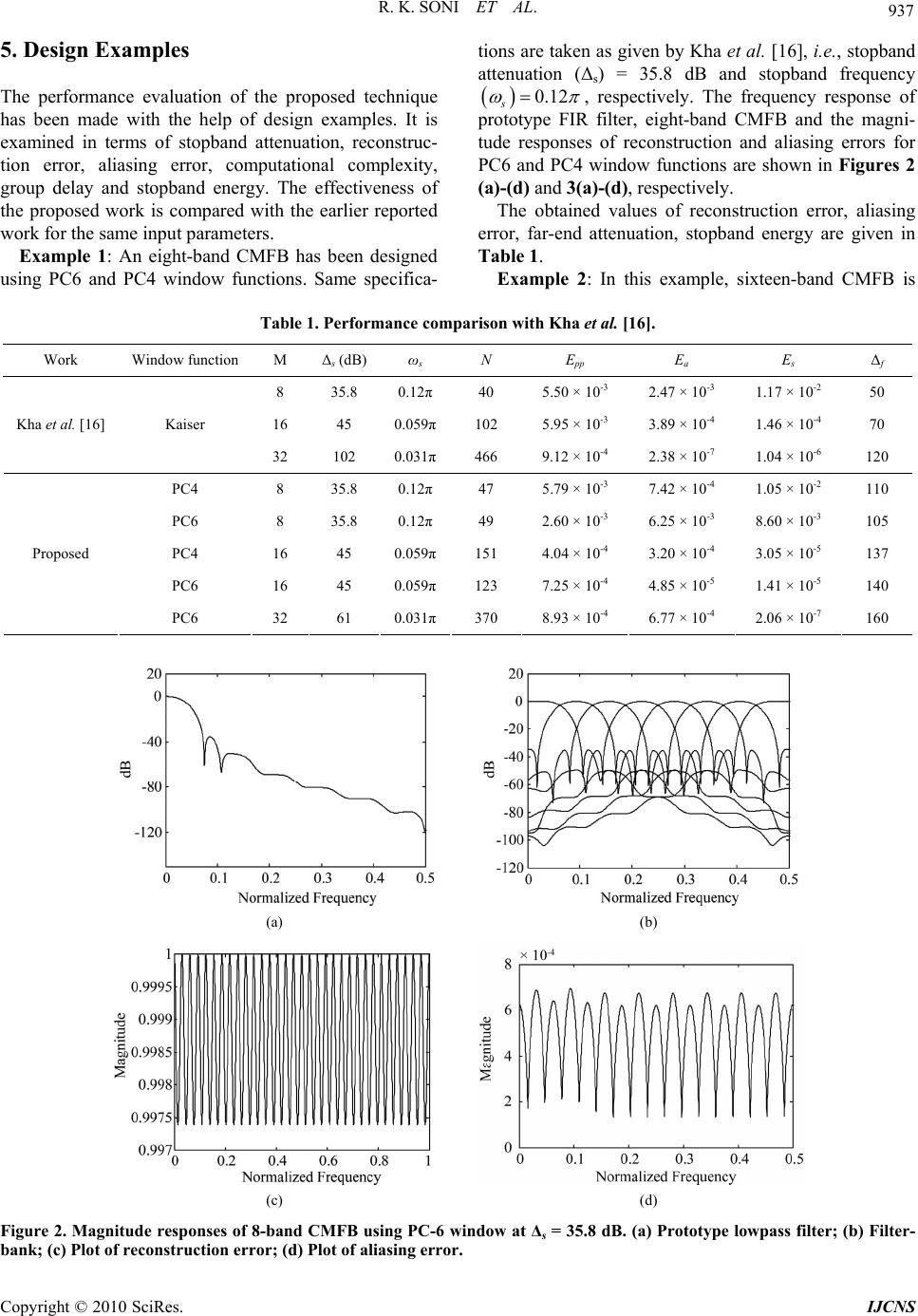

R. K. SONI ET AL.
937
5. Design Examples
The performance evaluation of the proposed technique
has been made with the help of design examples. It is
examined in terms of stopband attenuation, reconstruc-
tion error, aliasing error, computational complexity,
group delay and stopband energy. The effectiveness of
the proposed work is compared with the earlier reported
work for the same input parameters.
Example 1: An eight-band CMFB has been designed
using PC6 and PC4 window functions. Same specifica-
tions are taken as given by Kha et al. [16], i.e., stopband
attenuation (Δs) = 35.8 dB and stopband frequency


0.12
s

 , respectively. The frequency response of
prototype FIR filter, eight-band CMFB and the magni-
tude responses of reconstruction and aliasing errors for
PC6 and PC4 window functions are shown in Figures 2
(a)-(d) and 3(a)-(d), respectively.
The obtained values of reconstruction error, aliasing
error, far-end attenuation, stopband energy are given in
Table 1.
Example 2: In this example, sixteen-band CMFB is
Table 1. Performance comparison with Kha et al. [16].
Work Window functionM Δs (dB)ωs N Epp E
a E s Δf
8 35.8 0.12π 40 5.50 × 10-3 2.47 × 10-3 1.17 × 10-2 50
16 45 0.059π102 5.95 × 10-3 3.89 × 10-4 1.46 × 10-4 70 Kha et al. [16] Kaiser
32 102 0.031π466 9.12 × 10-4 2.38 × 10-7 1.04 × 10-6 120
PC4 8 35.8 0.12π 47 5.79 × 10-3 7.42 × 10-4 1.05 × 10-2 110
PC6 8 35.8 0.12π 49 2.60 × 10-3 6.25 × 10-3 8.60 × 10-3 105
PC4 16 45 0.059π151 4.04 × 10-4 3.20 × 10-4 3.05 × 10-5 137
PC6 16 45 0.059π123 7.25 × 10-4 4.85 × 10-5 1.41 × 10-5 140
Proposed
PC6 32 61 0.031π370 8.93 × 10-4 6.77 × 10-4 2.06 × 10-7 160
(a) (b)
(c) (d)
Figure 2. Magnitude responses of 8-band CMFB using PC-6 window at Δs = 35.8 dB. (a) Prototype lowpass filter; (b) Filter-
bank; (c) Plot of reconstruction error; (d) Plot of aliasing error.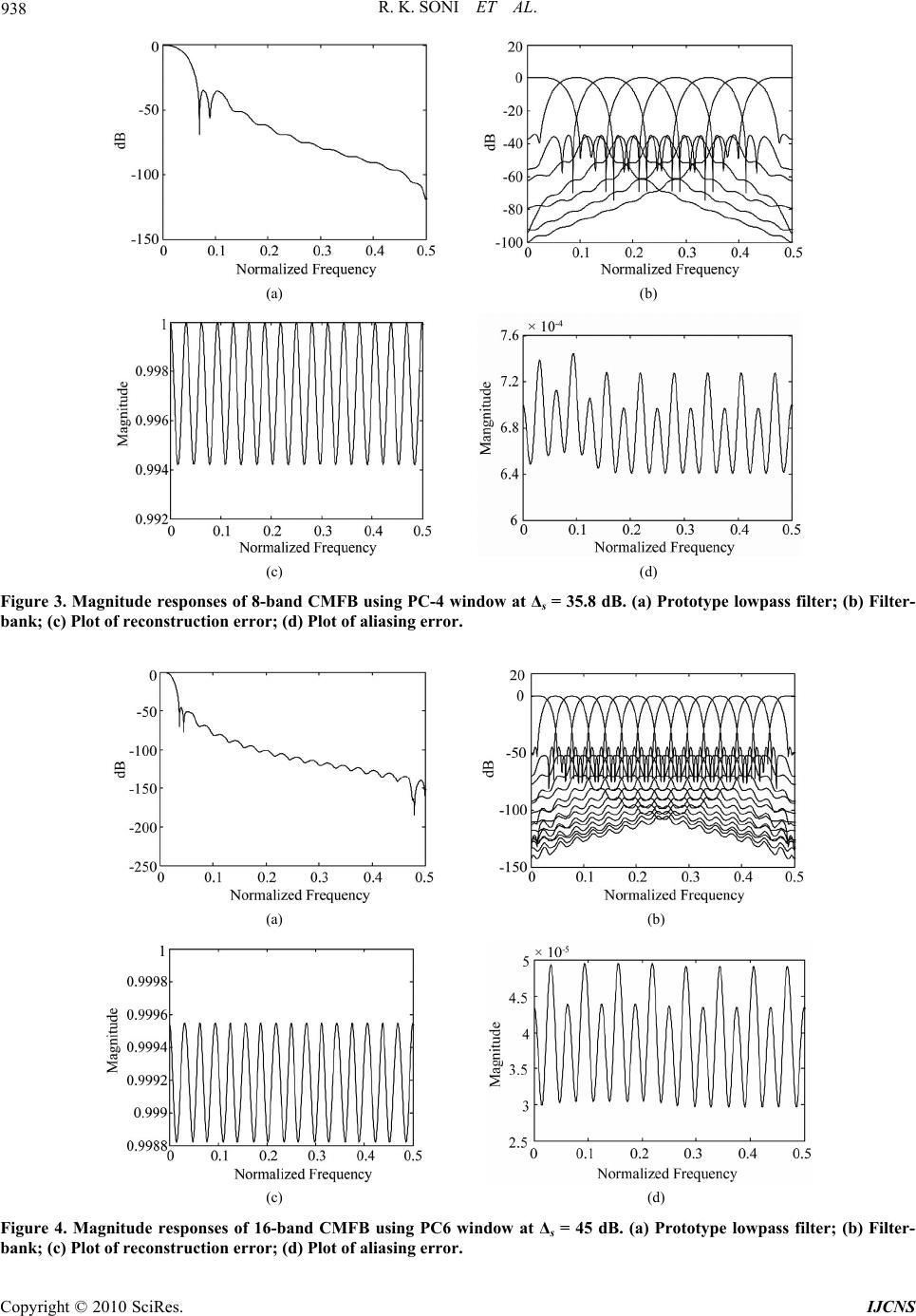

938 R. K. SONI ET AL.
(a) (b)
(c) (d)
Figure 3. Magnitude responses of 8-band CMFB using PC-4 window at Δs = 35.8 dB. (a) Prototype lowpass filter; (b) Filter-
bank; (c) Plot of reconstruction error; (d) Plot of aliasing error.
(a) (b)
(c) (d)
Figure 4. Magnitude responses of 16-band CMFB using PC6 window at Δs = 45 dB. (a) Prototype lowpass filter; (b) Filter-
ank; (c) Plot of reconstruction error; (d) Plot of aliasing error. b

R. K. SONI ET AL.
939
designed using same specifications as given in [16]. The
stopband attenuation and stopband frequency are taken
as (Δs) = 45dB, (
s

) = 0.0590

, respectively. The mag-
nitude responses of prototype FIR filter, 16-band CMFB,
reconstruction error and aliasing error for both window
functions are shown in Figure 4 and Figure 5, respec-
tively. The optimized value of performance parameters
are given in Table 1.
Example 3: A thirty two-band CMFB has been de-
signed using PC6 window function with the same stop-
band frequency as taken by Kha et al. [16]. Since, the
stopband attenuation for PC6 window functions is re-
stricted up to 68.69 dB, therefore, 61 dB stopband attenua-
tion is taken for the design. The frequency responses are
shown in Figures 6(a)-(d), respectively. The obtained
values of different parameters are given in Table 1.
6. Discussion
The comparative performance of proposed work with the
reported publication is given in Table 1. In case of
8-band CMFB the obtained values of reconstruction error
for PC4 and PC6 window functions is 5.79 × 10-3; 2.60 ×
10-4, respectively, which is smaller than the reported
value of Kha et al. [16]. Similarly, the aliasing error in
reported and proposed work is 2.47 × 10-3 and 7.42 ×
10-4, 6.25 × 10-3, respectively. Apart from lower values
of error parameters the proposed prototype filter using
combinational window functions are providing reduction
in stopband energy and better far-end attenuation in con-
trast to Kha et al.
Similarly, in case of 16-band CMFB the value of error
parameters are much smaller than the Kha et al. [16]
with smaller value of stopband energy and more far-end
attenuation. In 32-band CMFB the proposed technique
provides smaller value of reconstruction error than the
existing journal with less stopband energy and better
far-end attenuation.
7. Conclusions
An efficient design for M-band NPR CMFBs has been
proposed using combinational window functions. Simu-
lation studies shows that the developed algorithm provides
smaller values of error parameters than the previous pub-
lication. High values of SLFOR and far-end attenuation
(a) (b)
(c) (d)
Figure 5. Magnitude responses of 16-band CMFB using PC4 window at Δs = 45 dB. (a) Prototype lowpass filter; (b) Filter-
bank; (c) Plot of reconstruction error; (d) Plot of aliasing error.

940 R. K. SONI ET AL.
(a) (b)
(c) (d)
Figure 6. Magnitude responses of 32-band CMFB using PC-6 window at Δs = 61 dB. (a) Prototype lowpass filter; (b) Filter-
bank; (c) Plot of reconstruction error; (d) Plot of aliasing error.
provide significant reduction in stopband energy. These
filterbank can be used in real time applications such as
echo cancellation and cross-talk suppression.
8. References
[1] L. Lin and B. Farhang-Boroujeny, “Cosine-Modulated
Multitone for very High Speed Digital Subscribe Lines,”
EURASIP Journal on Applied Signal Processing, Vol.
2006, 2006, p. (19329)79.
[2] P. P. Vaidyanathan, “Multirate Systems and Filter Banks,”
Prentice-Hall, Englewood Cliffs, 1993.
[3] W. S. Lu, T. Saramäki and R. Bregovic, “Design of Prac-
tically Perfect-Reconstruction Cosine-Modulated Filter
Banks: A Second-Order Cone Programming Approach,”
IEEE Transactions on Circuits and System-I, Vol. 51, No.
3, May 2004, pp. 552-563.
[4] M. B. Furtado, P. S. R. Diniz and S. L. Netto, “Numeri-
cally Efficient Optimal Design of Cosine Modulated Fil-
ter Banks with Peak-Constrained Least-Squares Behav-
ior,” IEEE Transactions on Circuits and System-I, Vol.
52, No. 3, May 2005, pp. 597-608.
[5] M. B. Furtado, P. S. R. Diniz, S. L. Netto, and T. Saramäki,
“On the Design of High-Complexity Cosine-Modulated
Transmultiplexers Based on the Frequency-Response
Masking Approach,” IEEE Transactions on Circuits and
System-I, Vol. 52, No. 11, November 2005, pp. 2413-
2426.
[6] M. Blanco-Velasco, F. Cruz-Roldán, E. Moreno-Martínez,
J. I. Godino and K. E. Barner, “Embedded Filter Bank-
Based Algorithm for ECG Compression,” Signal Proc-
essing, Vol. 88, No. 6, June 2008, pp. 1402-1412.
[7] F. Cruz-Roldán and M. Monteagudo, “Efficient Imple-
mentation of Nearly-Perfect Reconstruction Cosine-Mo-
dulated Filterbanks,” IEEE Transactions on Signal Proc-
essing, Vol. 52, No. 9, September 2004, pp. 2661-2664.
[8] T. Q. Nguyen, “Near-Perfect-Reconstruction Pseudo QMF
Banks,” IEEE Transactions on Signal Processing, Vol.
42, No. 1, January 1994, pp. 65-76.
[9] C. K. Goh and Y. C. Lim, “Design of Two Channel Per-
fect Reconstruction Linear Phase FIR Filterbanks,” IEEE
Transactions on Circuits and System-II: Analog and
Digital Signal Processing, Vol. 45, August 1998.
[10] A. Jain, R. Saxena and S. C. Saxena, “An Improved and
Simplified Design of Cosine Modulated Pseudo-QMF
Filterbanks,” Digital Signal Processing, Vol. 16, No. 3,
May 2006, pp. 225-232.
[11] C. D. Creusere and S. K. Mitra, “A Simple Method for
Designing High-Quality Prototype Filters for M-Band

R. K. SONI ET AL.
941
Pseudo QMF Banks,” IEEE Transactions on Signal Pro-
cessing, Vol. 43, No. 4, April 1995, pp. 1005-1007.
[12] S. N. Sharma, R. Saxena and S. C. Saxena, “Design of
FIR Filters Using Variable Window Families: A Com-
parative Study,” Journal of Indian Institute of Science,
Vol. 84, October 2005, pp. 155-161.
[13] S. K. Mitra, “Digital Signal Processing—A Computer Based
Approach,” Tata McGraw-Hill Publishing Co. Ltd., New
Delhi, 1998.
[14] Y. Lin and P. P. Vaidyanathan, “A Kaiser Window Ap-
proach for the Design of Prototype Filters of Cosine
Modulated Filterbanks,” IEEE Signal Processing Letters,
Vol. 5, No. 6, June 1998, pp. 132-134.
[15] J. D. Johnston, “A Filter Family Designed for Use in
Quadrature Mirror Filter Banks,” Proceedings of IEEE
International Conference on Acoustics, Speech and Sig-
nal Processing, Denver, 9-11 April 1980, pp. 291-294.
[16] H. H. Kha, H. D. Tuan and T. Q. Nguyen, “Efficient De-
sign of Cosine-Modulated Filterbanks via Convex Opti-
mization,” IEEE Transactions on Signal Processing, Vol.
57, No. 3, 2009, pp. 966-976.

942 R. K. SONI ET AL.
Appendix
Specify sampling frequency, num-
ber of bands, stopband attenuation,
and passband ripple
Initialize passband and stopband
frequency. Calculate the cutoff fre-
quency, transition band, filter length
and window coefficients of selected
window function.
Initialize step size (step), search
direction (dir), flag, minimum value
of reconstruction error (e_err) and
initial value of reconstruction error
(p_err)
Design prototype filter and obtain
filters for synthesis and analysis
sections using Cosine modulation
scheme.
Calculated reconstruction error and
absolute value of objective function
(obj)
(

= + dir × step)
c c

p_err = obj
Display optimized value of reconstruc-
tion error
No
No
No
Is obj ≤ e_err
Is obj = p_err
Is obj > p_err
End
No
Yes
step = step/2
dir = –dir
Yes
Flag = 1
(comes
out from
loop)
Yes