 Creative Education 2010. Vol.1, No.3, 138-148 Copyright © 2010 SciRes. DOI:10.4236/ce.2010.13022 Language and Mathematics: Bridging between Natural Language and Mathematical Language in Solving Problems in Mathematics Bat-Sheva Ilany1, Bruria Margolin2 1Beit-Berl College, Israel; 2Levinsky College of Education, Israel. Email: bat77@013net, b ruria.margolin@gmail.com Received June 21st, 2010; revised August 25th, 2010; accepted September 18th, 2010. In the solution of mathematical word problems, problems that are accompanied by text, there is a need to bridge between mathematical language that requires an awareness of the mathematical components, and natural lan- guage that requires a literacy approach to the whole text. In this paper we present examples of mathematical word problems whose solutions depend on a transition between a linguistic situation on one side and abstract mathematical structure on the other. These examples demonstrate the need of treating word problems in a litera- cy approach. For this purpose, a model for teaching and learning is suggested. The model, which was tested successfully, presents an interactive multi-level process that enables deciphering of the mathematical text by means of decoding symbols and graphs. This leads to understanding of the revealed content and the linguistic situation, transfer to a mathematical model, and correspondence between the linguistic situation and the appro- priate mathematical model. This model was tested as a case study. The participants were 3 students: a student in the sixth grade, a student in the ninth grade and a college student. All the students demonstrated an impressive improvement in their mathematical comprehension using this model. Keywords: Mathematical Language, Word Problems Natural Language and Mathematical Language In the solution of word problems, that is to say in the solution of mathematical problems that are accompanied by text, the student is faced with two languages mixed together (Kane, 1970): natural language and mathematical language. One of the limitations of natural language is the fact that it works in a dia- chronic manner; the meanings it represents are interpreted ac- cording to a time frame. The perception of the world, and in fact the meaning of the world, depends on field synchronicity, the reciprocal relations with the environment. Furthermore, the field as a whole gives meaning to its parts, and each part of the field contributes meaning to the whole. In other words, to read a word problem in mathematics and to give it meaning, it is necessary to perceive the problem as a textual unit and not as a collection of data. A textual unit is a linguistic unit larger than a sentence. It’s semantic structure “consists of those elements and relations that are directly derived from the text itself [...] without adding an- ything that is not explicitly specified in the text” (Kintsch, 1998, p. 103). The linguistic unit is coherent from a content and lin- guistic point of view (Brown & Yule, 1983; Halliday & Hassan, 1976; Van Dijk, 1980; Widdowson, 1979), and is used for communication (Sarel, 1991, Margolin, 2002). Identification of the constituent parts of a text depends on meta-a w areness of the function of the form, the function of the word, and the function of the sentence in a text, especially awareness of symbols and syntactic awareness (Herriman, 1991 in MacGregor, & Price, 1999). Indeed, exercises like addition and subtraction or mul- tiplication and division are important for the understanding of the mathematical language, but the perception of the textual structure is a process by which you can identify textual com- ponents and carry out different logical operations. Mathematical language is a language of symbols, concepts, definitions, and theorems. Mathematical language needs to be learned and does not develop naturally like a child’s natural language. In mathematical language the child learns to recog- nize, for example, numbers as objects, one to one of their simi- lar and different properties. The child perceives the numbers as signs by means of which it is possible to calculate calculations and to do various manipulations. Syntax, generally, deals with configuration rules according to which sentences and words are constructed. The syntax of ma- thematical language includes lists of symbols, configuration rules for constructing language patterns, axioms, a deductive system, and theorems. Mathematical terms and symbols must be defined unambiguously. Likewise, every assertion in mathe- matical language is also unambiguous—every mathematical pattern has one deep structure that is determined by operational r ule s. We will not expand on definitions and theorems in mathe- matics, but each definition of a mathematical concept is the result of a complex process. Each definition contains additional concepts that also need to be defined. All mathematical theo- rems in all branches of mathematics are characterized by the fact that they are derived logically, deductively, and consis- tently from a system of elementary theorems – a xioms. Our central argument is that there is a bridge between ma- thematical language that necessitates seeing the mathe ma ti c- cal components, and natural language that demands textual literacy for the text as a whole. In other words, there is a bridge between the mathematical components and the literal compo- nents. When knowledge gaps in the mathematical language are  B.-S. ILANY & B. MARGOLIN large, natural language must supply what is missing, and be clear and explicit. However, when knowledge gaps in the ma- thematical language are small, natural language does not need to supply what is missing. Differences between Natural Language and Mathematical Language The fundamental differences between natural language and mathematical language derive first and foremost from the fact that mathematical language is more precise and less flexible than the structure of natural language. In natural language there are differences between surface structure and deep structure of the utterance, there are ambiguous statements that derive from ambiguous words, and there is a wealth of language. This wealth of language derives from the diversity of nouns, and from the diversity of words expressing relation - all the verbs and adjectives. On the other hand, in mathematical language for each surface structure there is one deep structure, all statements are unambiguous, and there is a paucity of language that ex- presses itself in the fact that there is only one type of noun – numbers, functions, etc., and that there are two relational signs – equality and inequality (Bloedy-Vinner, 1998). Different concepts are interpreted in the different languages – natural language and mathematical language – in different ways. The structure of mathematical language is more precise and less flexible than the structure of natural language, thus great tension is created in the use of natural language in mathematical problems. Let us take for example the concept diagonal. Diagonal in mathematical language is a straight-line segment that joins two non-adjacent vertices in a polygon. The diagonal can also pass through points outside the polygon, and can be at different angles. On the other hand, in natural language no mathematical rules apply to the diagonal and as evidence we can give as an example the following advert. According to the advert, it is forbidden to cross the road on a diagonal that is at an angle different from 90 degrees between the crossing and the sidewalk. The diagonal in the advert is not a mathematical diagonal, since it does not join two vertices of a polygon. Like the diagonal, the straight line is also different in mathe- matical language than in natural language. Whereas in natural language a straight line is a segment with a beginning and an end, in mathematical language it is a fundamental undefined concept, with no beginning and no end. Translating from Natural Language to Math ematical Language in Mathematical Word Proble ms A mathematical problem is a situation in which an individual or a group of people are asked to perform a task for which there is no immediately available algorithm that completely defines a solution method. Solving mathematical problems requires the imp lementation of a sequence of operations by means of which some final target is attained (Lester, 1978). A word problem in mathematics is an independent unit of text that comprises a question sentence and a speech event (Nesher, 1988; Nesher & Katriel, 1977). Sometimes the unit of text describes an event from daily life. The aim of the descrip- tion is to give expression to the logical structure that dictates a particular arithmetic operation. The difficulty with the solution of mathematical word problems is the need to translate the event described in natural language to arithmetic operations ex- pressed in mathematical language. The transition from natural language includes syntactic, semantic, and pragmatic under- standing of the discourse. Word problems in mathematics are divided into two types according to the topics they relate to. One type is mathematical word problems that deal with mathematical relationships between objective sizes, like: What is the number that is twice as big as the sum of 25 and 17? The other type is mathematical word problems that deal with real life situations, like: It takes 3 workers 5 hours to plough a field. How many hours would it take 2 workers to plough the same field? In this paper we will relate to every mathematical problem accompanied by text as a word problem in mathematics. There is a tendency in the professional literature to relate to a word problem as a textual unit that describes an everyday event, and the majority of papers and researches relate to problems not accompanied by an authentic background story as mathematical problems and not as word problems. Thus, this problem: “Find the equation of the straight line that is parallel to the straight line 3x – 7y = 4 and passes through the point (0, 10)” is not considered to be a word problem, rather a mathematical problem, since it is not accompanied by an authentic background story. An example for this could be Polya’s treatment in his book How to Solve It (1945) of mathematical problems accompanied by text as problems, although at the same time he suggested that for the problem to be understood it is first of all necessary for the verbal version to be understood. In our opinion, those problems must be defined as word problems since such problems include text that the solver needs to understand. We attempted to implement the teaching and learning model proposed in this paper with two kinds of mathematical problems: one, accompanied by an authentic background story that is considered to be a word problem in the professional literature; and another, not accompanied by an authentic background story, that is not considered to be a word problem in the professional literature. We argue that a mathematical problem with the follow ing properties is a word problem even when it is not accompanied by an authentic background story: it constitutes a coherent textual unit in terms of content and language; it has clear boundaries; it is used for communication; it contains two different languages mixed together: natural language and mathematical language (see the case of Shiri later). Following are examples of mathematical word problems, in which the solution of the problem depends on converting a linguistic situation into a mathematical model. These examples differ from each other in many varied aspects. The Soldiers and the Bus Problem Translation from natural language to mathematical language in mathematical word problems is problematic also because of the difference between solving an authentic realistic problem and solving a word problem in mathematics. An example of this is “The soldiers and the bus problem”: An army bus can transport 36 soldiers. 1128 soldiers need to be bused to training camp. How many buses are needed?  B.-S. ILANY & B. MARGOLIN The appropriate calculation is: 1128:36 = 31(12). The answer to the problem is 32 buses. 12 soldiers will go in the 32nd bus (or less than 36 soldiers will travel in some of the buses bus). In a research that was conducted among 13-year-old students only 23% answered this correctly, 19% answered 31 buses, and 29% gave as the answer 31 buses remainder 12 (Silver, Shapiro, & Deutsch, 1993). Contrary to the previous problem, where there was an attempt to connect the answer to the real situation, in this problem there is no such attempt. Apparently this is be- cause of the fact that the arithmetical solution is easily arrived at, and thus there is no need to connect the problem to the real situation.1 The Sheep and the Dogs Problem Students make the transition from natural language to mathe- matical language automatically even in problems that do not have a mathematical solution, because the norm in school is that if a problem is given, then it must have a solution. For example: Five dogs guard 125 sheep. How old is the shepherd? (Baruk, 1989) Students try to find a calculation, and they try to solve the problem through trial and error. They try to check different possible solutions by using the given numbers and ignoring the situation. They try solutions according to arithmetic operations, from the easy to the difficult, as follows: 1. By adding: 5 + 125 = 130 2. When the number seems to them to be too big to be a person’s age, the students try to solve the problem by subtracting: 125 – 5 = 120 3. When this number is also seems to be too big, they try to solve the problem by dividing: 125: 5 = 25. This solution seems to them to be reasonable. The Students and the Professor Problem An example of a mathematical problem and of the difficulty of translating from natural language is The Students and the Professor Problem (Kaput & Clement, 1979). This problem, which exposed the reversal in translation mistake, has been investigated in various researches (e.g., Clement, 1982; Ros- nick, 1981), and has been explained in different ways (Bloedy- Vinner, 1998). Write an algebraic expression using the variables S and P that will represent the following assertion: “In this university the number of students is 6 times greater than the number of professors”. Use S for the number of students, and P for the number of professors. When this problem was given to 150 first year engineering students and 47 social science students, 37% of the engineering students and 57% of the social science students got it wrong. Two thirds of the wrong answers contained reversed equations of the type 6S = P instead of 6P = S. The mistake derived from the fact that in natural language the order of the words deter- mines the meaning. The quantifier 6 appears beside the noun (students) and equality in the mathematical equation is not con- sidered. According to natural language, the students were represented by S, the arithmetic operation was represented by multiplication, and finally the professors were represented by P, and thus 6S = P. The problem of the students and the professor was given to eight fourth-year students specializing in mathematics for ele- mentary school at a teachers’ training college in Israel. Apart from one student who solved it correctly, all the other students erred, writing 6S = P instead of 6P = S. Here also, as in the a bove-mentioned cases, the mistake arose from the fact that in natural language the order of the words determines the meaning. The quantifier 6 appears beside the noun (students) and equality in the mathematical equation is not considered. The Reduced Number Problem Another example of a mathematical problem for which there is a need for transition from natural language to mathematical language is “The number that was reduced”: Write an equation, using the variable X, which represents the following assertion: “In this college a quarter of the number of students, which was reduced by 5, are mathematics students”. When this problem was given to students of mathematics education in a teachers’ training college, the following expr es- sions were given: 1. 2. The two above expressions are correct. The difference be- tween them derives from the fact that the surface structure ex- pressed in the assertion represents two deep structures. For each deep structure there is a different mathematical expression. In the first expression, the quarter was of the number of students in the college reduced by 5. Whereas in the second expression, the quarter was of all the students in the college, and only then was the number reduced by 5. Both answers are correct. The Combinations Problem Another example of a word problem for which misunder- standing the literal meaning caused a misunderstanding of the mathematical problem is Com binations (Woolf, 2005). The problem was presented during a fourth grade mathematics les- s on: In a parking lot there are 66 wheels, some of them belonging to cars, and some of them belonging to tricycles. What combi- nations of cars and tricycles can you find that have 66 wheels altogether? How could you know whether you have found all possible combinations? The combinations problem documented in Woolf’ s paper describes students’ inability to cope with the problem due to the fact that they did not understand the word combinations. Solu- tion of the mathematical problem described above focused on understanding the word combinations and understanding the logical structure of the whole text. To understand the problem, students are required more than command of the language. They need to learn to construct a meaningful body of knowl- edge from the information in the question, including data and a 1This problem was given in different countries (e.g., Norway, Japan, and Ireland) and in different populations, and the results were similar (Greer, 1997).  B.-S. ILANY & B. MARGOLIN solution scheme. In other words: they need to make a connec- tion between natural language and mathematical language. Towards Bridging between Natural Language and Mathematical Language As we saw above, the knowledge gaps between mathematical language and natural language emerge especially in the solution of word problems. Problem solving is an all-encompassing concept that includes many cognitive processes like, among others, literal and syntactic processing, changes of represe nta- tion, and algorithmic processing. Representation is an important area for problem solving and little is known about the relation- ship between inner comprehension and its external representa- tion. To bridge between natural language and mathematical language it is necessary to educate towards mathematical-linguistic literacy2, at the level of the addressor (speaker or writer) and at the level of the addressee (listener or reader). From the point of view of the addressor, he/she must ensure that the references in the text are related to suitable referents, that the expressions are not ambiguous, and that all the problematic terms are made clear. In other words, the addressor must display consideration for the recipient by supplying easily accessible and acceptable information. The addressor must take into account that the meaning of the text is a product of the interactions between the addressor’s schema and deductions, and the addressee’s schema and conclusions. Thus the addressor must first determine precise assumptions about the addressee’s knowledge and deductive abi l ity, to produce text as explicit as possible by means of linguistic implementation of his/her ideas. The addressor must predict detractors and obstacles that are liable to disturb understanding, and take steps to prevent them (Folman, 2000). As for the addressee, to extract the full meaning from the text he must fill in the missing information that is not found in the text. In other words, he/she must identify the information in the text in three circles of connection. The adjacent and literary connection (co-text) is the connection formed inside adjacent linguistic units. The circumstantial pragmatic connection (context) includes different components like the identity of the addressor and the addressee, the time and place of the discourse, the addressor’s intentions, and the communication medium (Nir, 1989). The connection with the universe of discourse that is in fact the connection formed between the text and the world (Sarel, 1991), is based on our previous knowledge of the particular subject area. The knowledge gaps in problem solving are between the textual unit and the hidden mathematical structure. The linguistic units in the text not only function as signs that have their signified object or idea in the world external to linguistics but also are connected to other fundamentals in the text, so that their meanings arise from the way the linguistic components are organized in the text. Moreover, not all the information is given explicitly in the text. There is information that can be derived by mathematical means on the basis of the explicit information. To bridge the gaps between natural language and mathe- matical language it is necessary to develop an awareness of these gaps by means of meaningful interactions between the student and his/her environment in the context of authentic activities. These authentic activities are activities that represent situations that describe a reality that is connected to the world of students and teachers in school and in the community (Ben- Chaim, Keret, & Ilany, 2006). A language develops by means of meaningful interactions between the individual and his/her environment in the context of authentic activities (Gee, 1996). The context of authentic activities enables education towards linguistic-mathematical literacy, because the interpr e ttation of the discourse is based to a great extent on analogy to our past experience, meaning that it is based on our socio-cultural knowledge (Brown & Yule, 1983). According to Greer (1997), the concepts addition, subtraction, multiplication, and division forcefully create models for situations, and students have to differentiate between the model and the situation and to assess whether the model is appropriate to the situation. The process of creating meaning for the context is multi-layered and is carried out at every layer of the text: at the syntactical, the semantic, and the pragmatic layers, at different levels of focusing. The interaction between the reader’s schemas and the schemas of the text necessitates communicative-cognitive effort. The communicative effort is expressed by the identification of the situation described, and the cognitive effort is expressed by the composition of the problem from new while combining within it the mathematical model. Bridging between natural language and mathematical language necessitates connecting the two faces of the word problem: the linguistic situation on one side and the abstract structures on the other (Greer, 1997). According to the professional literature, the bridging can be carried out in two different ways: by translation of the linguistic situation into abstract structures (Polya cited in Reusser & Stebler, 1997), and by organization of the unit of mathematical content (Freudental, 1991). In this paper we suggest making an interaction between the two methods in a processive approach by a model for the Instruction and Learning of the Solution of Mathematical Word Problems. Many researches that deal with varied subjects in the learn- ing of mathematics like, for example, real mathematics (De Lange, 1987), dilemmas in mathematics instruction based on different representations of concepts (Ball, 1993), solution of verbal questions (Nathan, Kintch, & Young, 1992), and learn- ing concepts like the concept of function (Kaput, 1993), main- tain that development of modeling skills is one of the important aims of a mathematics curriculum, and serves as a central pe- dagogical tool. Instruction Model for the Solution of Mathematical Word Prob le ms To bridge the gaps between natural language and mathe- matical language in solving word problems in Mathematics the researchers of this study developed an instruction model for the solution of mathematical word problems. The two researchers are teachers in two colleges in Israel. 2 There are many definitions of literacy. The abundance of definitions derives from the extension of the concept from the wr itten language connection and from language altogether. Today literacy represents also orientation and competence in any area, and thus there are those who prefer to relate to it in the plural, and to differentiate between different literacies: linguistic literacy, computer literacy, mathematical literacy,  B.-S. ILANY & B. MARGOLIN One of them is a teacher of Mathematics and the other is a teacher in Linguistics. The teacher of Mathematics has encoun- tered many difficulties of students in solving word problems. She realized that the difficulties emerged from understanding the text literally and mathematically. She decided to build a tool with a teacher in Linguistics to bridge the gaps between Ma- thematics and Linguistics. The two researchers began inter - viewing children asking what where the difficulties in solving word problems. A nine - stages instruction model was built after the interviews. In several cases, a third party, a colleague who teaches Mathematics was involved, and took part in the deliberation process until agreement was reached. After the model was built it was validated by six experts in Mathematics and Mathematics education. The nine–stage model was vali- da te d by 34 student-teachers specializing in mathematics teaching at a teachers’ seminary in a college in Israel. Only then it was used on three students: a student from elementary school, a student from Junior high school and a college student. The data were taken from word problems in Mathematics, in which these students were asked to answer in two stages: first they were asked to answer them without any instruction and then they were asked to answer them with this instructional model. Following is our nine-stage instruction model for the solution of mathematical word problems (schemas appear in the diagram that follows): Reading the Problem The first stage involves reading the problem from the bottom up, as a way of collecting the details. The action of reading at this stage is an exposure to the meaning, where the location of the meaning is in the text. The process of reading is an accu- mulative process from the smallest units (the words) to the largest units (the whole text). Understanding the Linguistic Situation The next stage involves reading the problem for a second time. The action of reading at this stage will be called in this paper the warming up stage: a multi- directional search as a way of brainstorming. At this stage the reader will ask himself the following questions: 1. Are all the words clear? 2. Are all the sentences clear? 3. What are the keywords? 4. Do I understand the keywords? 5. What is the question? 6. Do I understand the question? 7. How can I describe the problem in my own words? Understanding the Mathematical Situation We define the mathematical situation as the mathematical context of the problem, which relates to two types of information: the data and the question. The data relate to all the expressions that we assume to exist in the problem. They can appear in explicit form or in implicit form. The explicit data are those that are mentioned in the text, and the implicit data are axioms, theorems, and implicit facts that can be used in the solution of the problem. The question points in the direction of the expression we want to find. To understand the mathematical situation there is a need to examine the data and the question and to have a good grasp of the subject at hand. It is possible to be assisted, when necessary, by taking apart, demonstration, exercise, and illustration. In the first stage it is possible to break up the given problem into explicit data, implicit data, and a question, and in the second stage it is possible to demonstrate the problem with specific instances and to interpret the problem by means of a picture, a table, a diagram, or a graph, that can help to simplify the problem. A problem solver needs to identify the known facts and the logical-mathematical conditions of the problem—the connec- tions and relationships between the mathematical data and the logical analysis of the problem. In other words, the connections between the classical elements—nouns connected to numerical quantifiers in different sentences of the text and time-space relationships between objects or events that appear in the te xt—and the semantic relationship between the classical elements that are the verbs that appear in different sentences of the text (Nesher & Katriel, 1977; Hershkovitz & Nesher, 1996). At this stage the reader will ask himself the following ques- tions: 1. What is my relationship with the mathematical subject of the problem? 2. Is there a difficulty in the problem? 3. Are all the data clear? 4. Are there implicit data in the problem? (For example: in a problem that describes a working week, is the intention 7, 6, or 5 working days, as is usual nowadays?) 5. Are there superfluous data? (For example: in a problem accompanied there superfluous by a background story, are there superfluous data about the heroes?) 6. Do I understand the connection between the data in the question? 7. Is it possible to demonstrate the problem in particular i nstanc es? Matching the Mathematical Situation to the Linguistic Situation This stage involves reading the problem once more, from the top down. The action In the course of acquiring schemas the learner meets new cases and acts on them according to his/her previous schemas connected to the same matter. The learner expects a particular outcome. If the result marches his/her expectations, then an expansion of his/her existing schema takes place. If not, then there occurs a violation that could cause changes in the schema and the acquisition of a new schema. At this stage the solver needs to process the literal infor- mation for the of reading at this stage is the application of schemas on the text, where the location of the meaning is in the reader’s knowledge schemas. The process of reading at this stage is an accumulative process from the combining of mathe- matical knowledge schemas with the schemas in the text. A schema is a mental representation characterized by a fixed internal network of relationships that is created at a high level of abstraction or generalization and serves as a template that is used to clarify specific events (Brown & Yule, 1983; Hiebart & Carpenter, 1992). The schema is an activity pattern (Piaget,  B.-S. ILANY & B. MARGOLIN 1980) that enables its owner to act under the same conditions in a consistent manner by habit, and in addition it has a dynamic characteristic that allows it to expand in new conditions. Different definitions of schemas by different researchers appear in Hershkovitz and Nesher (2003). purpose of changing it into a mathematical exercise or an algebraic equation while focusing on the syntactic structure and the semantic structure of the problem. The problem with pro- cessing the information necessary for solving the word problem is one of the main difficulties in the solution of mathematical word problems. Processing the literal information for the purpose of changing it into a mathematical exercise or an algebraic equation is done by understanding the literal clues, that is the words that support (helpful clues) or the words that deceive (misleading clues) as clues for choosing the arithmetic operations needed to solve the problem. For example: the use of the words more or less (Nesher, Greeno & Reilly, 1982). At this stage the reader will ask himself the following ques- tions: 1. Do the nouns in the question appear again in a more general unit? (For example: given apples and later fruits. It is important that the problem solver understands that apple is a fruit.) 2. Do the connectives that appear in the question relate to different mathematical sizes? (For example: if some number is 7 and the product is x what is the multiplying number?) 3. Are there literal clues in the problem that is certain words that help as a clue for choosing the arithmetic operation required for solving the problem? 4. Is it possible to demonstrate the problem by means of a picture, a table, a diagram, or a graph? Bringing up Ideas for a Solution The meaning of solving a problem is to find an arrangement of steps starting from the given situation (in the problem) until the desired goal is reached, such that each step is derived from its predecessor by logical operations (acceptable in the context of the given problem). The process leading to a solution of the problem is connected to a suitable choice that is a search for a method, idea, or steps. It may be necessary to analyze the problem in different ways, to identify the problem before attempting its solution (Schoenfeld, 1980). To change the search to systematic, it is necessary to know problem-solving strategies. There exist general strategies, and strategies specific to different types of problems. Usua lly, students are given problems similar to those they solved in the past. Therefore, according to Polya (1945), there raises the question: Do you know a problem close to this one? In most cases there is no difficulty, according to Polya in bringing up problems that are already solved and are close in some way to the present problem. As far as using Polya’s theory, indeed we have not explained it in as much detail as Polya did, and the significance of his theory is much greater than presented here, yet from our experience and from case studies presented in this paper it is possible to see that for practical purposes the questions appearing in this section are likely to help the problem solver. At this stage the learner will ask the following ques- tions: 1. Is the problem unique 2. Have I encountered similar problems? 3. Is it possible to construct a schema for solving the problem on the basis of past experience? Screening the Ideas After raising different ideas for a solution of the problem, it is necessary to check each one of them, whether it truly helps to solve the problem. It is necessary to screen them, and to retain only relevant ideas. At this stage the learner will ask the following questions: 1. Does the idea help to solve the question? 2. How does the idea help to solve the question? Building a Mathematical Model Researchers who are concerned with the process of building a mathematical model for a phenomenon agree that the mean- ing of the process is mathematization of a phenomenon (Yeru- shalmi, 1997) or, according to Ormell’s (1991) version, a ma- thematical description of the whole phenomenon instead of checking isolated parameters in the phenomenon. Consequently, we define mathematical model building as constructing repre- sentations in mathematical language like an exercise or an equ- a t ion. At this stage the learner will ask the following questions: 1. What will I do as a first stage to solving the problem? 2. Do I know how to solve the problem and to build an ap- propriate mathematical model? 3. What mathematical model should I use to solve the prob- le m? The learner will construct a schema that represents the net- work of connections between his/her previous knowledge and the schemas in the mathematical text by means of an interaction with the following operations: defining the problem and com- prehending the situation it describes; building a mathematical model of the mathematical principles relevant to the problem; understanding the relationships and the conditions pertaining to the problem; and using of the mathematical model. Finding the Solution After finding the mathematical model, it is necessary to solve it to reach the expected solution. It is important to check if this is a unique solution or if there is another possible solution; all possible solutions must be found. At this stage the learner will ask the following questions: 1. Is the solution unique? 2. What are all the possible solutions to the problem? Control It is necessary to check that the solution to the problem is suitable to the problem itself. That is to say, it is necessary to return to the original problem, to read it again, and to check: 1. Does the solution make sense? 2. Is the solution appropriate to the linguistic situation? 3. Is the solution appropriate to the mathematical situation? 4. Does the mathematical model that I used fit the problem? This stage is the most important, because many times it seems as if we have found the solution, but the solution does not make sense (for example, we got 2.2 people), and so we 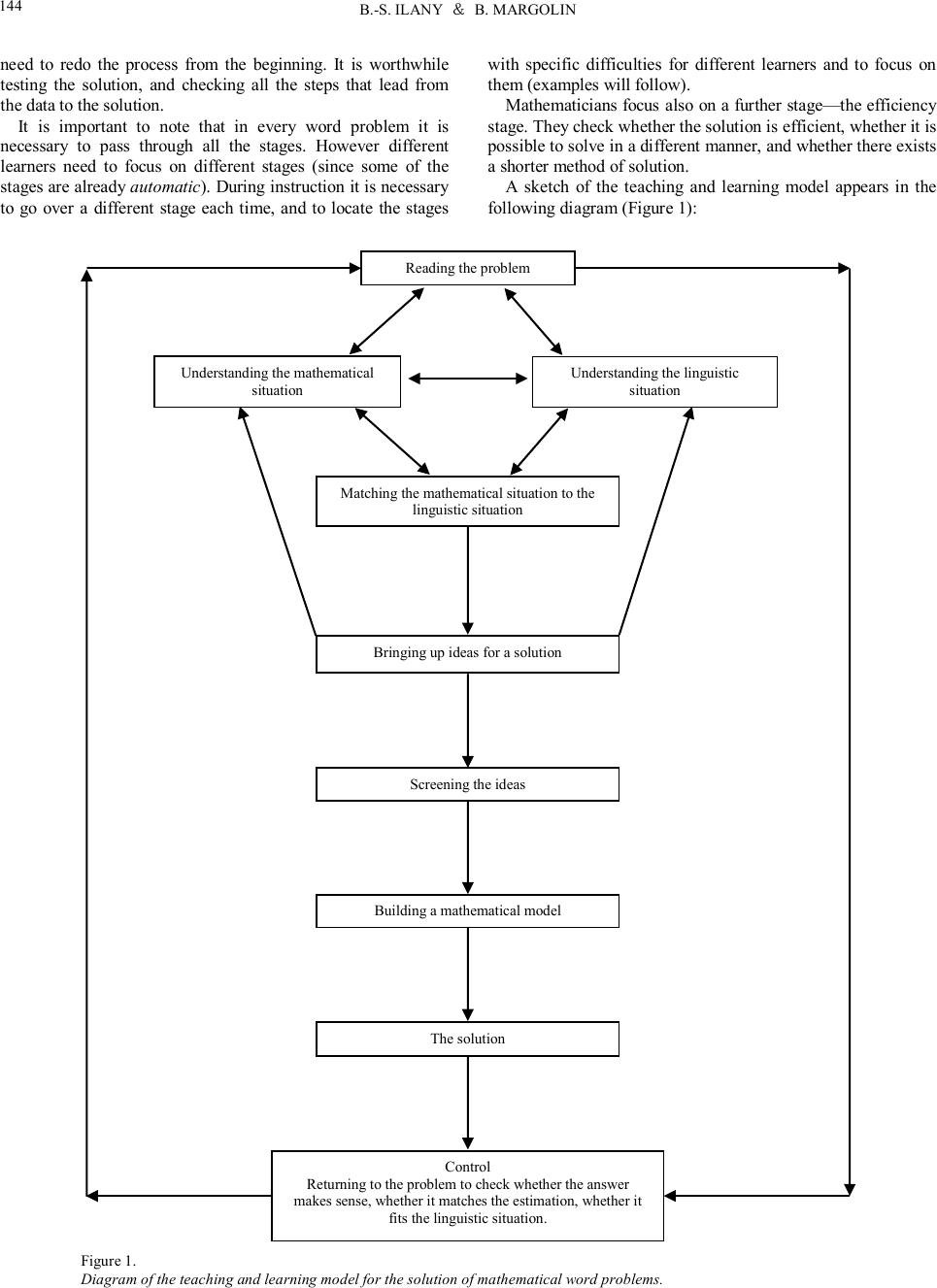 B.-S. ILANY & B. MARGOLIN need to redo the process from the beginning. It is worthwhile testing the solution, and checking all the steps that lead from the data to the solution. It is important to note that in every word problem it is necessary to pass through all the stages. However different learners need to focus on different stages (since some of the stages are already automatic). During instruction it is necessary to go over a different stage each time, and to locate the stages with specific difficulties for different learners and to focus on them (examples will follow). Mathematicians focus also on a further stage—the efficiency stage. They check whether the solution is efficient, whether it is possible to solve in a different manner, and whether there exists a shorter method of solution. A sketch of the teaching and learning model appears in the following diagram (Figure 1): Understanding the linguistic situation Understanding the mathematical situation Matching the mathematical situation to the linguistic situation Building a mathematical model Bringing up ideas for a solution Control Returning to the problem to check whether the answer makes sense, whether it matches the estimation, whether it fits the linguistic situation. Figure 1. Diagram of the teaching and learning model for the solution of mathematical word problems.  B.-S. ILANY & B. MARGOLIN Application of the Teaching and Learning Model To illustrate the model we bring 3 case studies: a student in the fifth grade, a student in the ninth grade and a college stu- dent. We attempted to apply the model both to mathematical word problems accompanied by an authentic background story, and to mathematical word problems not accompanied by a back- ground story. The Case of Yael Yael is a college student specializing in mathematics teach- ing at a teachers’ college in the center of the country. She was given the Students and Professors Problem described above, and she made the typical mistake, as found in the literature: 6S = P. After being taught the model, she solved the problem and got the correct solution: 6P = S. The student wrote down her working-process according to the instructional model as fol- lows: 1. Reading the problem –First of all I read the problem. 2. Understanding the linguistic situation – Next, I read the problem again. I asked myself if it is all clear (words and sentences), if I understand the question, and how I could describe the problem in my own words. Once it was clear to me that I understood all the words in the problem, I marked the key words: “times greater than”, “the students”, and “the professors”. I asked myself, what do they want me to do? What is the P and what is the S? And here is my description of the problem: The number of students is 6 times greater than the number of professors. 3. Understanding the mathematical situation – I checked whether I needed to describe the problem with an equation with letters. I think that it is not a problem that I need to find an actual result for, but that I have to give an equation. Then I realized that I have trouble with this sort of problem. The given information seems to be clear, but in fact you need to pay attention the concept “6 times”. It is important to analyze and understand which given is 6 times the other one. Under - standing the relationship between the two givens is important for the solution. 4. Matching the mathematical situation to the linguistic situation – I looked for verbal clues that might help me solve the prob- lem. In our case, the concept “times greater than” tells us to multiply by some amount and so that is the arithmetic operation we need to perform. Here, I started to draw a diagram to bring the given information into focus: Students Professors S P Their number is 6 times greater 5. Bringing up ideas for a solution – To solve the problem at this stage I have to build a schema. I’ve met problems like this in the past, and that will help me build the schema. I met problems with the concept “greater than”; to see links between a particular number and another. My ideas for the solution are: 6P = S; 6S = P; 6S > P; 6P > S 6. Screening the ideas – To solve the problem I check whether the ideas I came up with are relevant to the problem, and whether they help me to solve it. I think that the inequality 6P > S does not make sense because the number of students is 6 times bigger than the num- ber of professors. The inequality 6S > P makes sense, but does not solve the problem, because I multiplied the number of stu- dents by 6, and then made it even bigger. From the information given in the problem I know that S > P. That is, I did not add anything that helps me to solve the problem. For that reason I also discard the solution 6S = P. 7. Building a mathematical model – As I said in the previous stage while screening the ideas, I need to understand the situation - the correct representation of the problem - and to see whether I understood correctly the connections between the given pieces of information. In the previous stage I ruled out all the possibilities: 6S = P; 6S > P; 6P > S. Therefore the only solution that remained is 8. Finding the solution – In this case there is no numerical result, so the solution is 6P = S or in another form it could be written S: 6 = P. 9. Control – I chose to read the problem again, and again I noticed the fact that the number of students is 6 times bigger than the number of professors. It seems to me that my solution makes sense. In addition, I substituted numbers and checked myself, since I know that I have trouble with this type of problem and sometimes I do the opposite. The Case of Shiri Shiri is a good student in the ninth grade. She, however, had some difficulties in understanding and solving the following word problem that did not describe every day event and was not accompanied by an authentic background story. Shiri, was giv- en the following problem in a school te st: Find the equation of the straight line, parallel to the line 3x – 7y = 4, passing through the point (0, 10). In the school test Shiri answer incorrect to this problem. We interviewed Shiri and in the interview she claimed that she did not know how to solve this problem: “I do not understand what is written in the problem, so …either I do something or I do not do anything. Therefore, in the test I wrote y = 3x + 10 and that was not the correct answer”. Shiri explained that she took the 3x from the original equation and added 10 because the line passes through the point (0, 10)). To enable Shiri to solve the problem we used all the steps of the above model. 1. Reading the problem – At the first stage Shiri was asked to read the problem aloud. 2. Unde rstanding the linguistic situation – At this stage, once it was clear that Shiri understood all the words in the problem, we asked her to mark the keywords. Shiri marked them as follows: “equation of the straight line”, “parallel”, and “passing through the point” . 3. Understanding the mathematical situation – Despite the fact that Shiri understood all the words linguistically and marked the keywords, she did not yet understand the mathe- matical context. Shiri was asked to express what she thought the problem was about. She said, “To find a new line”. Shiri was asked whether the given information was clear and whether she understood the connections between the pieces of informa-  B.-S. ILANY & B. MARGOLIN tion and the problem. Shiri did not understand the connection between the given information and the problem, despite the fact that the general conceptual frame of the problem was clear to her – she knew what a straight line and a parallel line are. 4. Matching the mathematical situation to the linguistic situation – At this stage Shiri needed to process the verbal information to turn it into a mathematical exercise (equation). Shiri was asked a general question about straight lines, “What is the equation of a straight line?” Shiri answered and wrote down y = mx + n, but she claimed that in the question there was no equation of a straight line. Shiri was asked what she though “parallel” meant, and she answered, “A line that has the same (slope) m”. At this stage integration took place between Shiri’s schemas concerning the equation of a straight line and her schemas concerning the text. Shiri was asked to look at the equation written in the problem and to think how it might be possible to convert it into the equation of a straight line like the one she just wrote. Then Shiri said, “ I need to convert the equ- ation into the equation of a straight line. Oy! In the test I made a mistake. In the test I took the coefficient of x, the 3, and I related to it as if it were the slope and that is wrong. It is for- bidden to relate to the coefficient of x as if it were the slope, like I did in the test”. 5. Bringing up ideas for a solution – Shiri suggested mov- ing the 3x to the right-hand side and wrote –7y = 4 - 3x. Shiri did not know what to do, and said, “This is still not the familiar equation of a straight line. I do not know what to do with the minus”. Then Shiri was asked, “On the basis of your past ex- perience, can you convert this equation to the equation of a straight line?” Shiri said, “In fact I can move the –7y to the other side’ and then I would not have the problem of the minus”. 6. Screening the ideas – Shiri was asked, “Which idea would you chose to solve the problem?” Shiri showed the equa- tion 7y = 3x - 4 and claimed that it reminds her of the equation y = mx + n because there is no minus before the y. 7. Building a mathematical model – Shiri was asked, “What can you do now to bring the equation to the same form as the equation y = mx + n?” Shiri looked again at the equation and said that in her opinion she needs to “get rid of” the 7. 8. Finding the solution – After Shiri’s insight concerning the equation of a straight line and the meaning of a line parallel to the given line, Shiri solved the problem correctly. Shiri was asked whether this was the only solution. She answered, “Since this is a line parallel to a given line and passing through a cer- tain point there is only one solution.” 9. Control – Shiri was asked whether the solution made sense and met the conditions of the problem. She answered, “I think so.” When asked how she could check it, she substituted the point (0, 10) into the equation of the line and said, “I got a true statement, and the line is parallel to the given line, so my s olution is correct.” The Case of Sivan Sivan is a 6th grade student, who had some difficulties in un- derstanding and solving word problems. She said: “I cannot understand word problems. They have too many words in them and I do not understand what I have to do”. Sivan was given the following problem and was asked to solve it: Tom has a bottle containing three quarters liter of milk. He drank one third of the milk. How much did he drink? Sivan did not understand the problem and she said: “I do not know what to do”. To enable Sivan to solve the problem we used all the steps of the above model. 1. Reading the problem – First of all Sivan read the prob- le m. 2. Understanding the linguistic situation – Next, she read the problem again, and she found the key words: “drank” “con- taining” “three quarters liter of milk” “one third of the milk”. 3. Understanding the mathematical situation – Sivan pointed out that she needed to pay attention to the two givens: “three quarters of” and “one third of”. Sivan said that she does- n’t like fractions. 4. Matching the mathematical situation to the linguistic situation – Sivan was asked if there are clues that might help her to solve the problem. She said: “I think that one third of the milk tells me to multiply or maybe to subtract but I don't know what to do”. 5. Bringing up ideas for a solution – To solve the problem at this stage Sivan was asked if she met similar problems. She said that she had met problems like this in the past but only with integer numbers. We asked her to create a problem with integer numbers. She created a problem, as follows: “Tom has a bottle containing six liters of milk. He drank one third of the milk. How much did he drink?” Sivan's ideas for the solution of this problem were: 6 X1/3 or 6-1/3. 6. Screening the ideas – To solve the problem Sivan checked whether the ideas she came up to the problem that she created were relevant to the problem, and whether they helped her to solve it. She decided to implement her ideas for her problem to our problem and she said: “my ideas for the prob- lem are: 3/4 X1/3 or 3/4 -1/3”. 7. Building a mathematical model –Sivan did not know which idea is right and therefore she decided to draw a picture of the problem. Sivan decided that the subtraction did not make sense because of the picture that she drew. She said: “I can see in the picture what it means 1/3 of 3 /4”. Sivan built the ma- thematical model: 3/4 × 1/3 (Figure 2). 8. Finding the solution – Sivan found the solution: Tom drank ¼ liter of milk. She said that she is certain that this is the only solution because of her drawing. 9. Control – Sivan read the problem again and said: “The solution is logical, because of the drawing. In the drawing it is very clear that if you divide 3/4 to 3 you get 1/4”. C oncl usi on In this paper we have tried to show how it is possible to Figure 2. The mathematical model 3/4 × 1/3.  B.-S. ILANY & B. MARGOLIN bridge gaps between natural language and mathematical lan- guage in solving mathematical problems by means of an in- structional model, whereby the addressee processes the text cognitively. The process of dealing with the verbal text of the mathematical problem is multi-staged, and necessitates the implementation of a number of cognitive actions: interpreting symbols and graphs, understanding the substance, understand- ing the linguistic situation, finding a mathematical model, and matching between the linguistic situation and the appropriate mathematical model. This nine-stage instruction and learning model transforms into a complex thought process when fully understood and in- ternalized. It is a meta-cognitive process that contributes to students’ conceptualization (Natstasi & Clements, 1990). Know- ledge of meta-cognitive processes assists in problem solving and improves the ability to achieve goals. We recommend teachers to “hitch” mathematical language to natural language: to avoid problems that have no connection with reality, to avoid ambiguous problems, to explain to the students the differences between natural and mathematical languages and the possibility of combining them. We recommend teachers to make intelligent use of the in- struction and learning model suggested above, that is, to adapt the model and its various stages both to different populations of students and to the nature of the problems and their complexity. The instruction and learning model suggested here is suitable for students in the upper grades of elementary school, in middle and high schools, and in teacher training colleges. In elemen - tary school, the majority of problems available to students have a numerical solution with real –life meaning, and so it is im- portant to understand the situation described in them. In their continued studies in middle and high school students will have to cope with problems that do not necessarily have a numerical solution, and will have to use algebra to solve them. Graduated work on solution methods of word problems using schemas built in previous work on simply word –problem solving will enable students to cope with more complex prob- lems. Moreover, adapting the model for different students will enable teachers to help every student according to his/her needs and to pinpoint the focus of difficulty for each student. Intelligent use of the suggested model of instruction and learning will also help student teachers, both in their training and in their teaching practice. Understanding the model will allow the starting teacher to understand that meta-linguistic awareness, syntactic and semantic awareness, and awareness of mathematical schemas are necessary for solving problems in mathematics. Furthermore, the way the problem is worded and its correspondence to reality can significantly affect students’ ability to solve the problem. Re ferences Ball, D. H. (1993). With an eye on the mathematical horizon: Dilem- mas of teaching elementary school mathematics. The Elementary School Journal, 93, 373-397. doi:10.1086/461730 Ben-Chaim, D., Keret, Y., & Ilany, B. (2006). Yahas veproporzia – Mehkar vehoraha behachsharat morim lematematica (Ratio and proportion- research and teaching in mathematics teacher training). Tel-Aviv: Mofet Inst. Press. Bloedy-Vinner, H. (1998). The understanding of algebraic language in university preacademic students. Ph. D. dissertation, Jerusalem: Hebrew University. Brown, G., & Yule, G. (1983). Discourse analysis. Cambridge: Cambridge University Pres s. Clement, J. (1982). Algebra word problem solution: Thought processes under- lying a common misconception. Journal for Research in Ma- themat ics Education, 13, 16-30. doi:10.2307/748434 De Lange, J. 1987 (1987). Mathematics insight and meaning. Utrect, Holland: Rijksuniversiteit. Fischbein, E. (1987). Intuition in science and mathematics: An educa- tional approach. Dordrecht, Holland: Reidel Pub. Folman, S. (2000). Hafakat Mashmaut mitext: Hebetim Hakara- tiim-tiksortiim shel Heker Hasiah (Decoding meaning from a text: Cognitive and communicational aspects of discourse analysis). Tel-Aviv: Tel- Aviv University. Freudenthal, H. (1991). Revising mathematics education. Dordrecht, South Holland: Kluwer. Gee, J. P. (1996). Social Linguistics and Literacy, Ideology in Dis- course. Bristol, PA: Taylor & Francis. Gravermeijer, K. (1997). Commentary on solving word problems: A case study of modeling?. Learning and Instruction, 7, 389-397. doi:10.1016/S0959-4752(97)00011-X Greer, B. (1997). Modeling reality in the mathematics classroom: The case of word problems. Learning and Instruction, 7, 293-307. doi:10.1016/S0959-4752(97)00006-6 Halliday, M. A. K., & Hassan, R. (1976). Cohesion in English. London: Longman. Hershkovitz, S., & Nesher, P. (1996). The role of schemes in designing computerized environments. Educational Studies in Mathematics, 30, 339-366. doi:10.1007/BF00570829 Hershkovitz, S., & Nesher, P. (2003). The role of schemes in solving word problems. The Mathematics Educator, 7, 1-24. Hiebert, J., & Carpenter, T.P. (1992). Learning and teaching with un- der- standi ng. In: D. A. Grouns (Ed.), Handbook of research on ma- thematics teaching and learning (pp. 65-92). New York: Macmilla n. Kan e, R. B. (1970). The readability of mathematics textbooks revisited. The Mathematics Teacher, 63, 579-581. Kap ut, J. J. (1993). The urgent need for proleptic research in represen- tation of quantitative relationships. In: T. A., Romberg, E. Fennema and T. R. Carpenter (Eds.), Integrating research on graphical repre- sentation of functions (pp. 273- 311). London: Lawrence Earlbaum Associates. Kap ut, J. J., & Clement, J. (1979). Letter to the editor of JCMB. Jour- nal of Children’s Mathematical Behavior, 2, pp. 208. Kintsch, W. (1998). Comprehension: A Paradigm for Cognition. Cambridge, England: Cambridge University Press. Lester, F. K. (1978). Mathematical problem solving in the elementary school: Some educational and psychological considerations. In: L. L Hatfield and D. A. Bradbard (Eds.), Mathematical problem solving: Papers from a research workshop (ERIC/S MET) . Columbus, Ohio: Columbus. MacGregor, M., & Price, E. (1999). An exploration of aspects of lan- guage proficiency and algebra learning. Journal for Research in Ma- thematics Education, 30, 449-467. doi:10.2307/749709 Margolin, B. (2002). Al defusey lechidut bein tarbutiim [On inter- cultural coherence patterns]. Script – Journal of the Israel Associa- tion for Literacy, 5-6, 81-89. Nastasi, B. K., & Clements, D. H. (1990). Metacomponential function- ing in young children. Intelligence, 14, 109-125. Nathan, M. J., Kintsch, W., & Young, E. (1992). A theory of alge- bra-word- problem comprehension and its implications for the design of learning environments. Cognition and Instruction, 9, 329-389. doi:10.1207/s1532690xci0904_2 Nesher, P. (1988). Multiplicative school word problems: Theoretical approaches and empirical findings. In: J. Hiebert and M. Behr (Eds.), Number concepts and operations in the middle grades (pp. 19-41). Mahwah, NJ: L. Erlbaum Associates. Nesher, P., Greene, J. G., & Riley, M. S. (1982). The development of semantic categories for addition and subtraction. Educational Studies in Mathematics, 13, 373-394. doi:10.1007/BF00366618  B.-S. ILANY & B. MARGOLIN Nesher, P., & Katr iel, T. (1977). A semantic analysis of addition and subtraction word problem in arithmetic. Educational Studies in Ma- thematics, 8, 251-269. doi:10.1007/BF00385925 Nir, R. (1989). Semantika hivrit mashmaut vetikshoret (Hebrew seman- tics meaning and communication. Tel-Aviv: Open University. Ormell, C. (1991). How ordinary meaning underpins the meaning of mathe- matics. Learning of Mathematics, 11, 25-30. Piaget, J. (1980). Experiments in contradiction. Chicago and London: University of Chicago Press. Polya, G. (19 45). How to Solve it?. Princeton, NJ: Princeton University Pre ss. Reusser, K., & Stebler, R. (1997). Every word problem has a solution - the social rationality of mathematical modeling in school. Learning and Instruction, 7, 309-327. doi:10.1016/S0959-4752(97)00014-5 Rosnick, P. (1981). Some misconceptions concerning the concept of variable. Are you careful about defining your variables?. Mathemat- ics Teacher, 74, 418-420, 450. Sarel, Z. (1991). Mavo Lenituah Hsiah (Introduction to discourse analysis). Tel-Aviv : Or-Am. Schoennfeld, A. H. (1980). Teaching problem-solving skills. American mathematical monthly, 87, 794-805. doi:10.2307/2320787 Silver, E. A., Shapiro, L. J., & Deutsch, A. (1993). Sense making and the solution of division problems involving remainders: An examina- tion of middle school student's solution processes and their interpre- tation of solution. Journal for Research in Mathematics Education, 24, 117-135. doi:10.2307/749216 Van Dijk, T. A. (1980). Macrostructures: An interdisciplinary study of global structures in discourse. Ma hwah, N.J.: L. Erlbaum Associ- ates. Widdowson, H. G. (1979). Explorations in Applied Linguistics. Oxford, England: Oxford University. Woolf, N. (2005). Lilmod lelamed Mathematica leshem Havana beezrat mentorim (Teaching how to teach Mathematics for understanding with mentors). In: R. Lidor, et al (Eds.), Zematim Bamehkar Hahinuhi (Cross-Roads in Educational Research) (pp.223-248), Tel-Aviv: Mofet Inst. Press. Yerushalmi, M. (1997). Mathematizing qualitative verbal descriptions of situations: A language to support modeling. Cognition and In- struction, 15, 207-264. doi:10.1207/s1532690xci1502_3
|