Paper Menu >>
Journal Menu >>
 Applied Mathematics, 2010, 3, 542-554 doi:10.4236/am.2010.16072 Published Online December 2010 (http://www.SciRP.org/journal/am) Copyright © 2010 SciRes. AM A Series Solution for the Ginzburg-Landau Equation with a Time-Periodic Coefficient Pradeep G. Siddheshwar Department of Mathematics, Bangalore University, Central College Campus, Bangalore, India E-mail: pgsmath@gmail.com Received May 4, 2010; revised November 7, 2010; accepted November 12, 2010 Abstract The solution of the real Ginzburg-Landau (GL) equation with a time-periodic coefficient is obtained in the form of a series, with assured convergence, using the computer-assisted ‘Homotopy Analysis Method’ (HAM) propounded by Liao [1]. The formulation has been kept quite general to keep open the possibility of obtaining the solution of the GL equation for different continua as limiting cases of the present study. New ideas have been added and clear explanations are provided in the paper to the existing concepts in HAM. The method can easily be extended to solve complex GL equation, system of GL equations or even the GL equa- tions with a diffusion term, each having a time-periodic coefficient. The necessary code in Mathematica that implements the HAM for the current problem is appended to the paper for use by the readers. Keywords: Ginzburg-Landau Equation, Modulation, Nonlinear Convection 1. Introduction GL equations arise as a solvability condition in a wide variety of problems in continuum mechanics while deal- ing with a weakly nonlinear stability of systems, e.g., one comes across the GL equation with constant and real coefficients in the case of Rayleigh-Bénard convection in fluids wherein instability sets in as a direct mode (also called stationary mode). When the Hopf mode (also called oscillatory mode) is the preferred one, like in viscoelastic liquids or as in constrained systems, the GL equation has complex yet constant coefficients. In certain other prob- lems one may also come across a system of GL equa- tions with constant coefficients. There are inhomogene- ous GL equations also. When one considers problems in which gravity expe- rienced in a fluid-based system is perturbed by a time-periodic vibration of the system, then the GL equa- tion turns out to be an equation like the one considered in the paper and the same has been solved here using the HAM, as propounded by Liao[1-5]. One may extend the solution procedure to other types of GL equations men- tioned earlier. The great advantage in using the method is that it gives the solution of non-linear equations in the form of a series whose convergence is assured. The me- thod is illustrated here in unabridged form using the ex- ample of the GL equation with a time-periodic coeffi- cient. The readers may refer to Liao [1-5] and others [6-13] for many other versatile applications of the method. 2. The GL Equation with a Time-Periodic Coefficient and its Solution by the HAM The GL equation with a time-periodic coefficient in the most general form is (see the appendix of the paper for the derivation of the equation in the context of a physical situation): 3 12 1sin , A QAQA (2.1) where A is the amplitude of convection, and are the frequency and small amplitude of the gravitational vibration (also called gravity modulation), 1 Q and 2 Q are constant coefficients (real) that are functions of the parameters of a given problem. We have used just in place of 2 used in the appendix. The initial condition to solve Equation (2.1) is: 0 0, A a (2.2) where 0 a is a prescribed initial value of the amplitude. The quantities 1 Q, 2 Q, and 0 a in Equations (2.1) and (2.2) have deliberately been left unspecified to keep open the possibility of obtaining a general result from the study that is applicable to different continua. This is one of the salient features of the study.  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 543 It must be noted here that in the absence of gravity modulation, i.e., =0, Equation (2.1) is the exactly sol- vable Bernoulli equation, viz., 3 12 A QAQ A and the unsteady solution of this GL equation, subject to condi- tion (2.2), is given by: 1 1 2 2 11 2 220 ()1 1. Q QQ Ae QQa (2.3) When the amplitude () A is small, however, the Bernoulli equation reduces to 1, A QA (2.4) Whose solution, subject to Equation (2.2), is 1 0. Q A ae (2.5) Thus we see that the amplitude grows exponentially to begin with (see solution (2.5)) but the growth is damped by the 3 A term as shown by the solution (2.3). One can easily see that for the case =0, Equation (2.1) has one steady solution () 0,A for all values of 1 Qand 2 Q, and a second steady solution 1 2 () , Q AQ for 1 2 0. Q Q The second steady state solution for =0 and the initial condition (2.2) are vital information for our writ- ing down an initial solution 0()A of the GL equation. The initial solution may be taken in the form: 0101 ,Aaaae (2.6) where 1 1 2 Q aQ and is as yet unspecified. The de- termination of can and will be dealt with at the time of seeking a series solution of the GL equation with a time-periodic coefficient. Quite obviously 0 A has been so chosen that it satisfies the conditions A 1 a and 0A0 a. The choice of the form of 0()A is most im- portant in obtaining a convergent series solution by the HAM and this aspect will be discussed much later in the paper. Now we discuss the problem in the presence of mod- ulation. One cannot in this case arrive at a useful analyt- ical solution as above, independent of numerical integra- tion, and resorting to numerical methods seems the only option. As a better option, alternately, we propose the HAM to obtain the series solution. To that end we define the following two notations: ,LAA A (2.7) 3 12 1sin ,NAA QAQA (2.8) where is the same as that used in Equation (2.6) and as said earlier it will be dealt with at the time of obtaining a series solution of the GL equation with a time-periodic coefficient. The particular choice of L in Equation (2.7) is suggested by the fact that the initial solution 0()A go-es as e . We throw more light on this in the next sec- tion. The proceeding of the paper thus far does give a feel- ing that many things are open ended but the reader we reassure that at the end of it all the inevitable postpone- ment of certain discussions to the end of the paper be- comes clear. Now we move on to the remaining part of the method involving construction of the solution of the given nonlinear equation by means of concepts borrowed from topology. In the HAM we obtain the solution of the equation NA0 (2.9) By constructing a homotopy from 0()A to the re- quired solution () NL A of Equation (2.9) using the ser- vices of what is called as an embedding parameter [0,1]p .As we see later p=0 and p=1 correspond to 0()A and () NL A respectively, where the subscript NL indicates that the solution is of the nonlinear problem. Henceforth, we use a suggestive notation ;p in place of A which indicates that the embedding pa- rameter has been brought into picture. Now we use the Maclaurin series for ;p around p=0 and this gives us: 1 ;;0 , m m m pAp (2.10) where 0 1;1,2,3,. ! m mm p Apm mp (2.11) Observing Equation (2.10), together with Equation (2.11), we find that () NL A can be determined provided various p-derivatives of ;p can be found at p=0. To obtain these derivatives we need a differential equa- tion for ;p . The required equation for ;p can be constructed using LA and NA , and we also remind ourselves at this point that (; )p varies from 0 A to NL A as p varies from 0 to 1. The required equation that fits this bill is: 0 1; ;,pLpApNp (2.12) where is an auxiliary parameter whose role in the control of convergence of the HAM-series solution will become apparent further on. In view of the above obser- vation, may also be called as the convergence-control parameter.  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 544 We are interested in ;1 NL A which is the solution of the given nonlinear Equation (2.1), now writ- ten in the form (2.7). Substituting p=1 in Equation (2.10) and noting that 0 ;0 A , we get 0 1 . NL m m AA A (2.13) From Equation (2.13) it is clear that the solution NL A of the given nonlinear Equation (2.1), subject to the condition (2.2), will be obtained as a series. Liao [4] proved a convergence theorem that is applicable to the series (2.13). The convergence is certain by the HAM as a consequence of the convergence theorem (see p. 18 of Liao [4]) but how to have the best possible convergence, or rather fast convergence, is the question. This is a mat- ter of discussion later on in the paper in the context of discussing the role of a certain to-be-introduced parame- ter controlling convergence. The initial condition to solve Equation (2.12) can be obtained from Equation (2.2) as: 0 (0; ).pa (2.14) Equations (2.12) and (2.14) are called the zeroth-order deformation equations as per the notion of deformation, as used in topology. Deformation has been made possible to be used in the method due to the parameter p that al- lows the varying of ;p from 0 A to NL A as it varies from 0 to 1. Now, in order to obtain the p-derivatives of ;p , we differentiate m-times the zeroth-order deformation equations with respect to p. To make use of the notation m A defined in Equation (2.11) we set p=0 in the re- sulting equations and also divide by m!. The above pro- cedure results in the following infinite system of linear equations: 11 ,1,2,3, mmm mm LAAR Am (2.15) subject to the initial condition 00, 1,2,3,. m Am (2.16) In the Equation (2.15) we have used the following no- tation: 0when1, 1when 1, m m m (2.17) 1012 1 ,,,, ,1 mm AAAAAm (2.18) and 1 11 0 1;,1. 1! m mm m p RAN pm mp (2.19) On using the definition of ;Np , from Equa- tion (2.8), we see that Equation (2.19) results in the fol- lowing equation: 111 1 1 21 00 1sin ,1,2,3,. mm mm mk mkkj j kj RAA QA QAA Am (2.20) We now make an analysis of both the equation and the possible nature of its solution. Firstly, the to-be-obtained series solution must encompass the solution of Equation (2.1) for the limiting case 0, as well as a periodic solution of the Equation (2.1) for small amplitudes, viz., 11sin . A QA . Let the solution of the above li- miting cases be denoted respectively by E A and A . These have the form: 1 2 0 mQ Em m Abe (2.21) 0 sincos , nn n Ann (2.22) where the coefficients m b, n and n are constants that may be functions of the parameters of the problem. The form of the solution (2.21) follows from the fact that E A is essentially the exact solution (2.3) in a bino- mially expanded form. Secondly, after discussing about the solution of the limiting cases, we note that the solu- tion NL A of the full Equation (2.1) must be such that it has an oscillatory and decaying nature as . The solution NL A must, in addition, have the two limiting solutions as part of its series solution. Let us now make a passing remark in regard to the choice of . The solution (2.21) does suggest that 1 =2Q but a dis- cussion in favour of this choice by estimating an error is given just before the section on results and discussion. At this point let us pause a bit and recollect what we have done and what is it that resulted out of it. In seeking the solution of the nonlinear differential equation by HAM we constructed a homotopy using an embedding parameter. The construction of homotopy and the proce- dure thereafter resulted in an infinite system of inhomo- geneous linear equations with the nonlinear term being part of the inhomogeneity. We now move on to solve the system of linear inho- mogeneous equations, as many as are required by a pre- determined convergence criterion. At this juncture while getting ready to solve the system of equations, we notice that waits to be defined. We will deal with the matter of choice of an appropriate value for in what follows. As a prologue to what is to follow we may, however, add here that a good choice of serves the purpose of con-  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 545 centrating a major part of the sum of the series (2.12) in its first few terms and thereby rendering the remaining terms vanishingly small. This, in essence, speaks of the convergence of the series (2.12) and its control through . We now move on to solve the system of linear Equa- tion (2.15), with 1mm RA given by Equation (2.20), and also discuss about the way an appropriate can be chosen. On using the definition (2.7) and denoting 1mmm AA by ()B , Equation (2.15) may now be written as: 1. mm dB BRA d (2.23) Equation (2.23) is an inhomogeneous linear differen- tial equation that has an integrating factor e . Multip- lying Equation (2.23) by e , the equation may be rear- ranged into the following form: 1. mm deeRA dB (2.24) Integrating the exact differential equation (2.24), we get 1 0 0, mm t BB eeRAdt (2.25) where t is a dummy variable of integration. Reverting back from B to the original functions, we get on re- arrangement the solution of the Equations (2.15) and (2.16) in the form: 10. t mmm mm A AeeRAtdt (2.26) By means of Mathematica, or such other packages, one may easily complete the integration in Equation (2.26). In fact, the solution (2.26) may be obtained using Ma- thematica itself and how this is done is demonstrated in the code attached. Thus, we see that it is easy to get the series solution of Equations (2.1) and (2.2) provided we fix the issues relating to and , and also the choice of .L 3. Choice of , and L At various stages in the paper this issue had to be insuffi- ciently addressed and discussions on them had to be post- poned to the point at which one is better equipped to handle the matter. The time now is just about right to dis- cuss these matters and we move in that direction. We first take the issue of . To determine an appropriate , we define a residual error in the form: 02 3 12 0 0 11sin R EAQ AQAd (3.1) where 0 is long enough to capture the error in full. We have to choose an optimum value of , denoted as opt , that yields the solution NL A , for a given accuracy, with minimum possible residual error. In other words, opt is corresponding to an extrema of the curve RR EE. Thus opt has to satisfy the following conditions: 2 2 0and0. RR dEdE dd (3.2) From the above discussion the rationale behind the in- troduction of becomes clear. The most important thing is that is a helpful parameter that influences conver- gence of the HAM series solution (2.13) but the conver- gent solution (the sum of the series 2.13) is independent of the choice of , as proved by Liao [4]. We now move on to the discussion on the choice of . We know from the exact solution (2.3) for the limiting case 0 that the solution decays quicker than e as . By substituting the initial guess (2.6) into Equa- tion (2.1) we can obtain a condition which on being sa- tisfied ensures that the solution decays faster than e as . The initial guess (2.6) cannot obviously sa- tisfy the equation (2.1) exactly and its introduction in the latter equation results in an error that is given by: 2 01 10112 2 23aa QeaaaQe (3.3) The choice 1 2Q clearly allows to decay faster than e . In view of this we set 1 2Q in the paper. The choice of an appropriate L involves issues re- lated to the decision of taking the initial solution in a particular fashion. The initial solution 0 A is chosen in such a way that its nature is akin to the nature of the HAM solution NL A . Thus the choice of Land the choice of 0 A are inter-related. Now we dwell on another important related issue involving the method. The most natural question that comes to the mind of a reader while going through the discussion on the chosen form of the deformation Equation (2.12) is the following: Why not have the following equation in place of the deformation Equation (2.12)? 1; ;,pL ppNp (3.4) where L can be taken to be the linear part of the given nonlinear equation. In the present problem L would in this case be 1.LQ (3.5) The solution of 0LA , subject to condition (2.2), would then be given by equation (2.5). Such a choice of 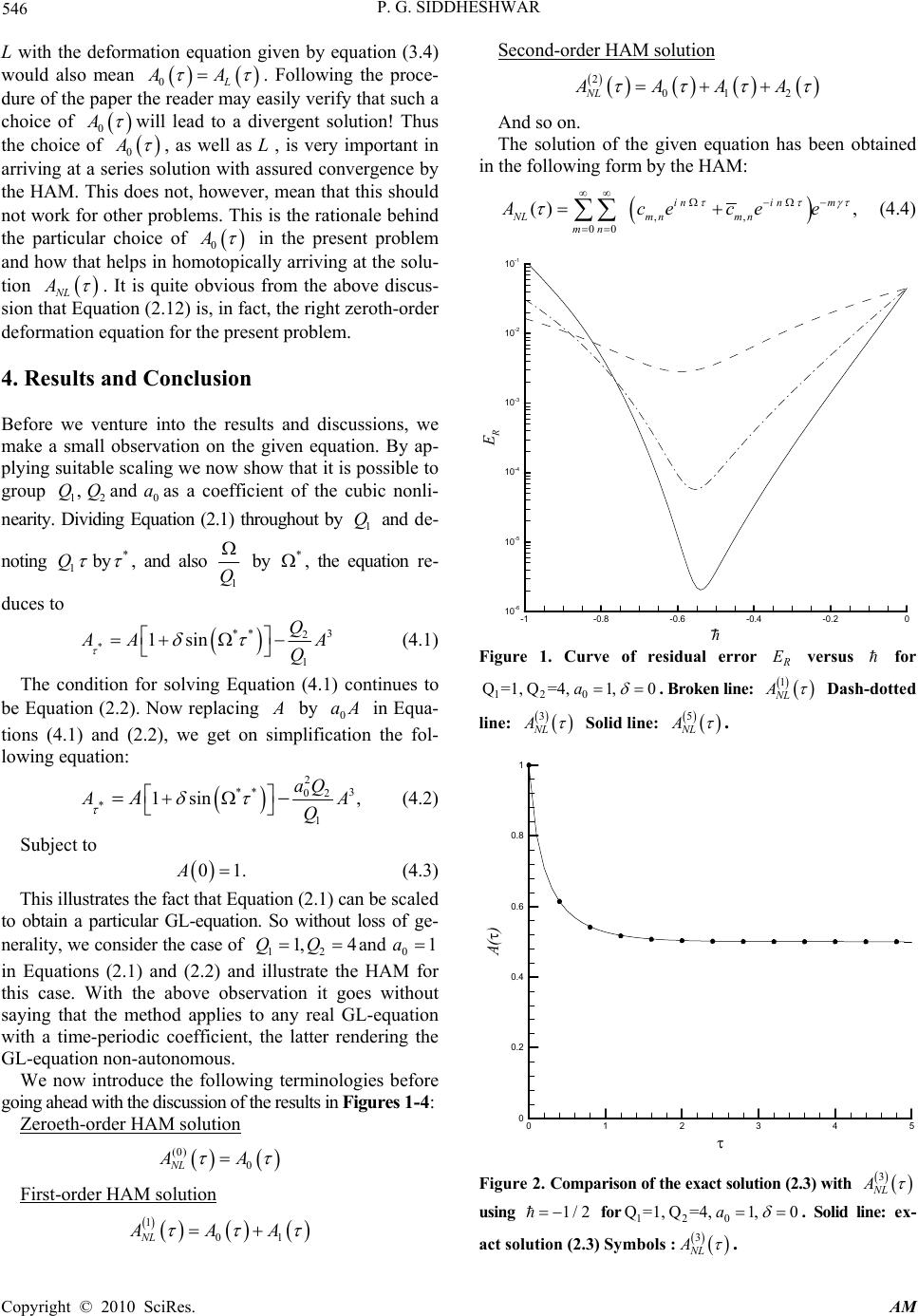 P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 546 L with the deformation equation given by equation (3.4) would also mean 0L AA . Following the proce- dure of the paper the reader may easily verify that such a choice of 0 A will lead to a divergent solution! Thus the choice of 0 A , as well as L , is very important in arriving at a series solution with assured convergence by the HAM. This does not, however, mean that this should not work for other problems. This is the rationale behind the particular choice of 0 A in the present problem and how that helps in homotopically arriving at the solu- tion NL A . It is quite obvious from the above discus- sion that Equation (2.12) is, in fact, the right zeroth-order deformation equation for the present problem. 4. Results and Conclusion Before we venture into the results and discussions, we make a small observation on the given equation. By ap- plying suitable scaling we now show that it is possible to group 120 ,andQQ aas a coefficient of the cubic nonli- nearity. Dividing Equation (2.1) throughout by 1 Q and de- noting 1 Q by * , and also 1 Q by * , the equation re- duces to * ** 3 2 1 1sin Q A AA Q (4.1) The condition for solving Equation (4.1) continues to be Equation (2.2). Now replacing A by 0 aA in Equa- tions (4.1) and (2.2), we get on simplification the fol- lowing equation: 2 ** 3 02 * 1 1sin , aQ A A Q A (4.2) Subject to 01.A (4.3) This illustrates the fact that Equation (2.1) can be scaled to obtain a particular GL-equation. So without loss of ge- nerality, we consider the case of 12 0 1,4 and1QQ a in Equations (2.1) and (2.2) and illustrate the HAM for this case. With the above observation it goes without saying that the method applies to any real GL-equation with a time-periodic coefficient, the latter rendering the GL-equation non-autonomous. We now introduce the following terminologies before going ahead with the discussion of the results in Figures 1-4: Zeroeth-order HAM solution (0) 0 NL AA First-order HAM solution 1 01 NL AAA Second-order HAM solution 2 012 NL AAAA And so on. The solution of the given equation has been obtained in the following form by the HAM: ,, 00 () , inin m NLmn mn mn Acecee (4.4) h E R -1 -0.8 -0.6 -0.4 -0.20 10 -6 10 -5 10 -4 10 -3 10 -2 10 -1 _ Figure 1. Curve of residual error R E versus for 120 Q=1, Q=4,1,0a . Broken line: 1 NL A Dash-dotted line: 3 NL A Solid line: 5 NL A . A() 0 1 2 3 4 5 0 0.2 0.4 0.6 0.8 1 F i g u r e 2 . Compari son of the exac t soluti on (2.3) wit h 3 NL A using 1/2 for120 Q=1, Q=4,1,0a . Solid line: ex- act solution (2.3) Symbols : 3 NL A . 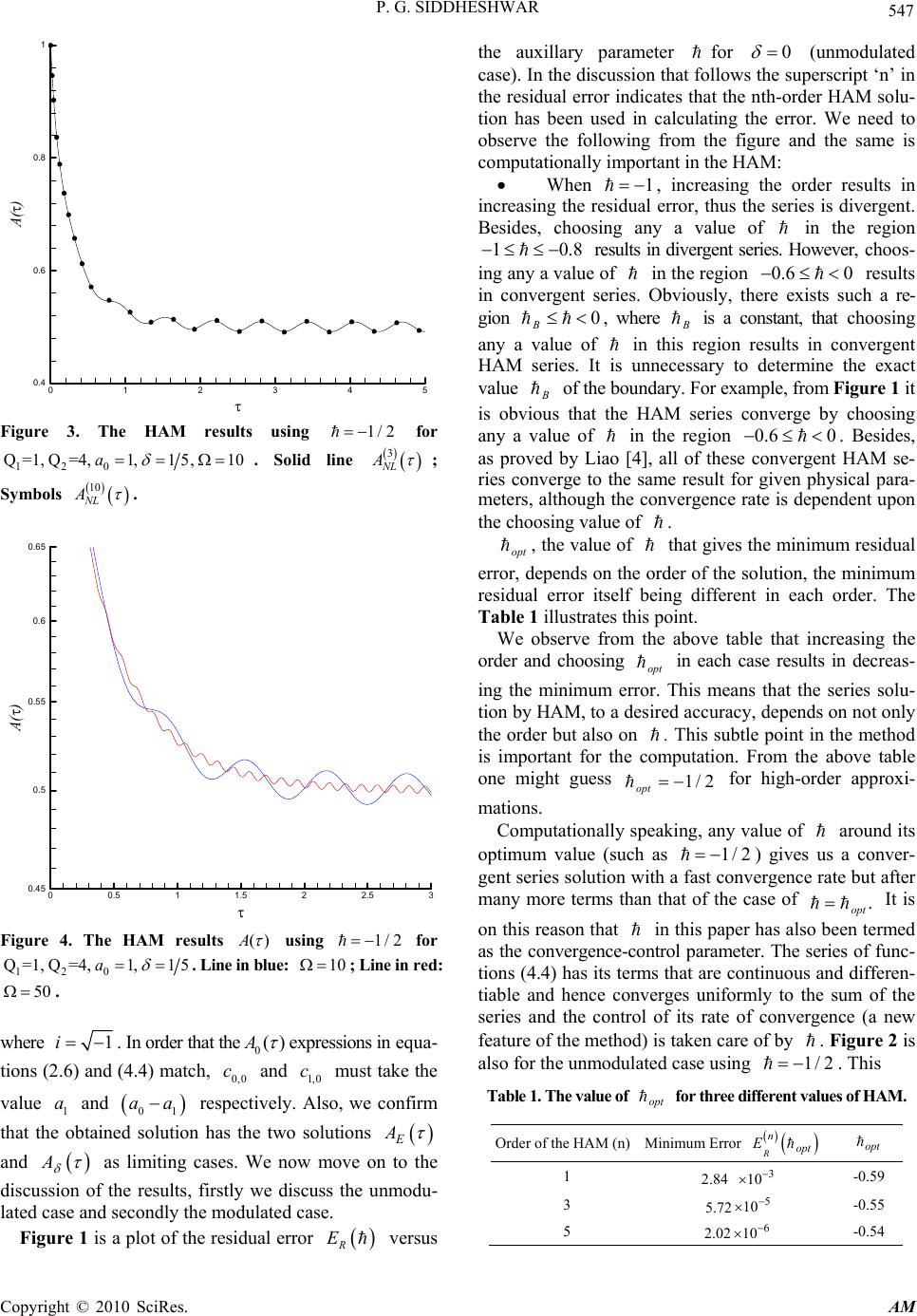 P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 547 A() 0 1 2 3 4 5 0.4 0.6 0.8 1 Figure 3. The HAM results using 1/2 for 120 Q=1, Q=4,1,15,10a . Solid line 3 NL A ; Symbols 10 NL A . A() 00.5 11.5 22.5 3 0.45 0.5 0.55 0.6 0.65 Figure 4. The HAM results ()A using 1/2 for 120 Q=1, Q=4,1,15a . Line in blue: 10 ; L ine i n red: 50 . where 1i. In order that the0()A expressions in equa- tions (2.6) and (4.4) match, 0,0 c and 1,0 c must take the value 1 a and 01 aa respectively. Also, we confirm that the obtained solution has the two solutions E A and A as limiting cases. We now move on to the discussion of the results, firstly we discuss the unmodu- lated case and secondly the modulated case. Figure 1 is a plot of the residual error R E versus the auxillary parameter for 0 (unmodulated case). In the discussion that follows the superscript ‘n’ in the residual error indicates that the nth-order HAM solu- tion has been used in calculating the error. We need to observe the following from the figure and the same is computationally important in the HAM: When 1 , increasing the order results in increasing the residual error, thus the series is divergent. Besides, choosing any a value of in the region 10.8 results in divergent series. However, choos- ing any a value of in the region 0.60 results in convergent series. Obviously, there exists such a re- gion 0 B , where B is a constant, that choosing any a value of in this region results in convergent HAM series. It is unnecessary to determine the exact value B of the boundary. For example, from Figure 1 it is obvious that the HAM series converge by choosing any a value of in the region 0.6 0. Besides, as proved by Liao [4], all of these convergent HAM se- ries converge to the same result for given physical para- meters, although the convergence rate is dependent upon the choosing value of . opt , the value of that gives the minimum residual error, depends on the order of the solution, the minimum residual error itself being different in each order. The Table 1 illustrates this point. We observe from the above table that increasing the order and choosing opt in each case results in decreas- ing the minimum error. This means that the series solu- tion by HAM, to a desired accuracy, depends on not only the order but also on . This subtle point in the method is important for the computation. From the above table one might guess 1/2 opt for high-order approxi- mations. Computationally speaking, any value of around its optimum value (such as 1/2) gives us a conver- gent series solution with a fast convergence rate but after many more terms than that of the case of . opt It is on this reason that in this paper has also been termed as the convergence-control parameter. The series of func- tions (4.4) has its terms that are continuous and differen- tiable and hence converges uniformly to the sum of the series and the control of its rate of convergence (a new feature of the method) is taken care of by . Figure 2 is also for the unmodulated case using 1/2 . This Table 1. The valu e of opt for three different values o f HAM. Order of the HAM (n)Minimum Error R n opt E opt 1 2.84 3 10 -0.59 3 5.725 10 -0.55 5 2.02 6 10 -0.54  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 548 shows the matching of the third-order HAM solution with the exact solution (2.3). In the modulated case (0 ), we use the same pro- cedure for finding opt as that in the unmodulated case. Figure 3 shows the matching of the results of the third-order and tenth-order HAM solutions using 1/ 2 , thereby implying that the third-order solution is good enough for the modulated case also. With an improper choice of (including the value -1) this would not have been the situation. We would, in that case, have slowing down of convergence or even divergence as the case may be. Figure 4 shows the convergent solution (using 1/2 ) of the tenth-order HAM solution for two values of . Clearly the effect of increasing is to decrease the amplitude. We observe in Figures 1-4 that the obtained ampli- tudes () () k NL A are quite small. This can be offered an explanation as given in what follows. For large , one can get the asymptotic expression 0101 11 ()cos sinAaaae From Equation (2.23). Substituting this into Equation (2.1), and neglecting the high-order terms, one gets the error E in the form: 11211 12 3sin3cos.EQ QQ Setting 11211 12 30and30QQ Q , the amplitude of the harmonic terms turns out to be 22 12 22 1 /9Q .Since ranges from 0.01 to 0.2 and 10 , the amplitude is rather small, as shown in the four figures. Figure 5 is a plot of the Nusselt number ()Nu , de- fined in Equation (A25) of the appendix, versus slow time for two different values of . Clearly the ef- fect of increasing frequency is to decrease the magnitude of the Nusselt number, thereby also meaning that heat transfer in a Rayleigh-Bénard convective system can be regulated using vibration of the system in the vertical direction, viz, gravity modulation. A physical problem involving a nonlinear differential equation with a time- periodic coefficient has been solved in series-form using the HAM and it is possible to do the same with other types of GL-equations as discussed in the introduction to the paper. The Mathematica program that implements the HAM in this paper is recorded in appendix B. 5. Conclusions The series solution by HAM is a good alternative to the numerical solution of the Ginzburg-Landau equation Nu() 0 1 2 3 8 9 10 11 12 Figure 5. The HAM results ()Nu using 1/2 for 120 Q=1, Q=4,1,15a . Line in blue: 10 ; Line in red: 50 . with a time-periodic coefficient, as so it is for many other non-linear differential equations—both ordinary and par- tial (see [2-11]). 6. Acknowledgements The author is grateful to the Bangalore University for grant- ing him leave to pursue collaborative research with Prof. Shijun Liao, to the Shanghai Jiao Tong University, China for making available its excellent facilities and to Shijun Liao for financial support, excellent discussions and kind hospitality during his month-long visit. 7. References [1] S. J. Liao, “On the Proposed Homotopy Analysis Tech- niques for Nonlinear Problems and its Application,” Ph. D. Thesis, Shanghai Jiao Tong University, Shanghai, 1992. [2] S. J. Liao, “Homotopy Analysis Method: A New Analyt- ical Technique for Non-Linear Problems,” Communica- tions in Non-linear Science & Numerical Simulation, Vol. 2, No. 2, 1997, pp 95-100. [3] S. J. Liao, “An Explicit, Totally Analytic Approximate Solution for Blasius’ Viscous Flow Problems,” Interna- tional Journal of Non-Linear Mechanics, Vol. 34, No. 4, 1999, pp. 759-778. [4] S. J. Liao, “Beyond Perturbation-Introduction to the Ho- motopy Analysis Method,” CRC Press, London, 2003. [5] S. Liao and Y. Tan, “A General Approach to Obtain Series Solutions of Nonlinear Differential Equations,” Studies in Applied Mathematics, Vol. 119, No. 4, 2007, pp. 297-354.  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 549 [6] S. Abbasbandy, “The Application of the Homotopy Analysis Method to Nonlinear Equations Arising in Heat Transfer,” Physics Letters A, Vol. 360, No. 1, 2006, pp. 109-113. [7] S. Abbasbandy, “The Application of Homotopy Analysis Method to Solve a Generalized Hirota-Satsuma Coupled KdV Equation,” Physics Letters A, Vol. 361, No. 6, 2007 pp. 478-483. [8] T. Hayat and M. Sajid, “On Analytic Solution for Thin Film Flow of a Fourth Grade Fluid Down a Vertical Cy- linder,” Physics Letter A, Vol. 361, No. 4-5, 2007, pp. 316-322. [9] M. Sajid, T. Hayat and S. Asghar, “Comparison Between the HAM and HPM Solutions of Thin Film Flows of Non-Newtonian Fluids on a Moving Belt,” Nonlinear Dynamics, Vol. 50, No. 1-2, 2007, pp. 27-35. [10] K. Yabushita, M. Yamashita and K. Tsuboi, “An Analytic Solution of Projectile Motion with the Quadratic Resis- tance Law Using the Homotopy Analysis Method,” Journal of Physics A: Mathematical and Theoretical, Vol. 40, 2007, pp. 8403-8416. [11] F. M. Allan, “Derivation of the Adomian Decomposition Method Using the Homotopy Analysis Method,” Applied Mathematics and Computation, Vol. 190, No. 1, 2007, pp. 6-14. [12] A. Alizadeh-Pahlavan, V. Aliakbar, F. Vakili-Farahani, and K. Sadeghy, “MHD Flows of UCM Fluids above Porous Stretching Sheets Using Two-Auxiliary-Parameter Homotopy Analysis Method,” Communication in Nonli- near Science and Numerical Simulation, Vol. 14, No. 2, 2009, pp. 473-488. [13] V. Marinca, N. Herisanu, and L. Nemes, “Optimal Ho- motopy Asymptotic Method with Application to Thin Film Flow,” Central European Journal of Physics, Vol. 6, No. 3, 2008, pp. 648-653.  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 550 APPENDIX A Derivation of the Time-Periodic Ginzburg-Landau Equation Consider the classical Rayleigh-Bénard problem with gravity modulation (or g-jitter as it is called). The con- servation of mass, linear momentum and energy in the problem are respectively governed by: .0 q (A1) 02 ˆ . () qqqp ggkq t (A2) 2 . TqT T t (A3) where q is the velocity, 0 is the density at the refer- ence temperature 0 T (temperature of the upper plate), p is the pressure, is the density, g is the acceleration due to gravity, g is the time-dependent gravity mod- ulation due to the vibration of the Rayleigh-Bénard setup, is the dynamic coefficient of viscosity, T is the tem- perature and is the thermal diffusivity of the liquid. The equation of state is given by 00 1TT (A4) where is the coefficient of thermal expansion. Let us consider the two-dimensional convection in the x-y plane with velocity components in the x and y direc- tions denoted by u and v respectively. Now eliminating the pressure p between the x- and y-components of the linear momentum equation, introducing the stream func- tion and using the equation (A4) in the resulting equation, we get 2 24 0 , 10, gt T gg txgxy (A5) Introducing into the equation (A3), we get 2ψTψT -χT+ - =0, τxy yx (A6) The equations (A5) and (A6) are rendered dimension- less using the following scaling: Space coordinates d Time 2 d χ Temperature T where d is the vertical distance between the parallel low- er and upper bounding plates of infinite horizontal extent and T is the temperature difference between the lower hot plate and the upper cold plate. Using the above scal- ing, equations (A5) and (A6) turn out to be: 2 24 , 11 1, T gm R PrtxPrxy (A7) 2ψTψT -T=- +, txyyx (A8) where . g t gm g (A9) The boundary condition to solve equations (A7)-(A8) in dimensionless form is: 2 2 0and1 on 0 0and0on 1 ψ=ψ= T=y=, ψ=ψ= T=y=. (A10) The conduction profile is ψ=0, and T=1-y (A11) Now we impose finite-amplitude perturbations on the basic quiescent state (A11) as ψ=Ψ(x, y,t),T=1-y+Θ(x,y,t). (A12) 222 1 4 1 ΨΨ Ψ+Ψ-Ψ Prtx yyx θ =R +gm+Ψ x ∂∂∂∂∂ ∇∇∇ ∂∂∂∂∂ ∂∇ ∂ (A13) Θ ΨΘΨΘΨ +--=Θ t xyyxx (A14) where Pr and R are respectively the Prandtl and Rayleigh numbers. The boundary condition (A10) for the perturbations reads as: 0and10 0and0 1 2 2 Ψ== Ψ Θ= on y=, Ψ== Ψ Θ= on y=., ∇ ∇ (A15) We now use the following asymptotic expansion in equations (A13) to (A15): 2 02 23 12 3 23 123 RR R (A16) where 0 R is the critical value of the Rayleigh number at which convection sets in when gravity modulation is absent. We use the time variations only at the slow time scale 2 τ=εt and () g m is taken to be: 2 2sin.gm=ε (A17)  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 551 At the lowest order, we have 4 1 0 2 1 0 0 Rx x (A18) The solution of the lowest order system is 1 12 Ψ=Asink xsinπy c kc Θ=Acoskxsinπy c δ (A19) The system (A18) gives us the critical value of the Rayleigh number and the wave number for stationary onset and their expressions are given below: 4 27 . 02 R=, kc 4 (A20) Amplitude Equation (Ginzburg-Landau equa tion) and Heat Transport for Stationary Instability At the second order, we have 4221 0 2 222 Ψ Rx Θ x (A21) where 21 11 11 22 0 , x yyx (A22) The second order solution can be obtained as: 2 22 22 A 8πδ c Ψ=0, . k Θ=- sin2πy, (A23) The horizontally-averaged Nusselt number, Nu , for the stationary mode of convection(the preferred mode in this problem) is given by 2 2/ (1 ) 200 2/ (1 ) 200 C c c c k kydx y xy Nu k kydx y y (A24) Substituting equation (A23) in equation (A24) and completing the integration, we get 2 2 2. δ c kA Nu= 1+4 (A25) At the third order, we have 4331 0 2 332 , Rx x (A26) where 2 1 21 31 02 0 1 sin Pr RΘ RRx (A27) 12 32 ΨΘ - τ x y (A28) Substituting , 1 Ψ and 2 Θ from equations(A19) and (A23) into equations (A27) and (A28), we get 2 2 0 2 0 2 sinsin sin 31 sin sin c c kA R Rkxy R Akxy c Pr (A29) 32 33 22 cossin 3sincossin 4 cc cc kA k kxyyAkxy (A30) The solvability condition for the existence of the third order solution is: 31 032 2 1ˆˆ 0, 00 c k Rdxdy yx (A31) where 2 ˆ()sinsin , ˆ()cossin . c c c ΨAkxy k Θ A kx y (A32) From equation (A31), on substituting equations (A29), (A30) and (A32) into the equation and completing the integration, we get the Ginzburg-Landau equation for stationary instability with a time-periodic coefficient in the form: 3 2 122 0 sin , R dA QAQA dR (A33) where 22 0 12 4 Pr and . 41 Pr 1 cc kPrR k QQ Pr (A34) The main paper deals with the solution of equation (A33) using the HAM, subject to the initial condition 0 0, A awhere 0 a is a chosen initial amplitude of convection. In calculations we may assume 20 RR to keep the parameters to the minimum.  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 552 APPENDIX B Mathematica Program for the Problem (**********************************************************************************) ( *Computer-Assisted HAM Series Solution of *) (* Ginzburg-Landau equation (2.1) (with g-jitter) *) (* subject to initial condition (2.2) *) (**********************************************************************************) (* *) (* A'-Q1*[1+delta*sin(omega*tau)]*A+Q2*A^3 = 0, A(0)=a0 *) (* *) (* November 16, 2009 *) (**********************************************************************************) (**********************************************************************************) (* Define GetR[k] using equation (2.20) *) (**********************************************************************************) GetR[k_]:=Module[{temp,j,n,sint}, sint = (Exp[omega*t*I]-Exp[-omega*t*I])/2/I; temp[1] = Sum[a[n]*aa[k-1-n],{n,0,k-1}]; temp[2] = at[k-1]-Q1*(1+delta*sint)*a[k-1]+Q2*temp[1]; R[k] = Expand[temp[2]]; ]; (**********************************************************************************) (* Set initial guess A[0] using equation (2.6) *) (**********************************************************************************) a1 = Sqrt[Q1/Q2]; a[0] = a1 + (a0-a1)*Exp[-gamma*t]; A[0] = a[0]; At[0] = D[U[0],t]; (**********************************************************************************) (* Define the function chi_{k} using equation (2.17) *) (**********************************************************************************) chi[k_]:=If[k<=1,0,1]; (**********************************************************************************) (* Define derivatives of a(t) and an intermediate sum required in equation (2.20) *) (**********************************************************************************) GetAll[k_]:=Module[{temp}, at[k] = D[a[k],t]//Expand; aa[k] = Sum[a[n]*a[k-n],{n,0,k}]//Expand; ]; (**********************************************************************************) (* Define L *) (**********************************************************************************) L[f_]:= D[f,t] + gamma*f; (**********************************************************************************) (* MOST IMPORTANT!! *) (* The code works best if the solution of equation (2.15) is obtained by Mathematica! It saves on time *)  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 553 (* by doing this way and hence this procedure is adopted in the program in the following three *) (* segments of the code. On a similar reason we have not used the trigonometric sine function directly *) (* in the code *) (**********************************************************************************) (**********************************************************************************) (* Define the inverse of L *) (**********************************************************************************) Linv[f_]:=Block[{temp,g,G,s}, temp = DSolve[L[g[t]] == f,g[t],t]/.C[_]->0; G = g[t]/.temp; s = G[[1]]//Expand; Expand[s] ]; (**********************************************************************************) (* Define the linearity of inverse of L, i.e., Linv[f_+g_] := Linv[f] + Linv[g]; *) (**********************************************************************************) Linv[p_Plus] := Map[Linv,p]; Linv[c_*f_] := c*Linv[f] /; FreeQ[c,t]; (**********************************************************************************) (* Define the residual error using equation (3.1) *) (**********************************************************************************) GetErr[k_,tmax_]:=Module[{temp,sint}, sint = (Exp[omega*t*I]-Exp[-omega*t*I])/2/I; error[k] = At[k] - Q1*(1+delta*sint)*A[k] + Q2*A[k]^3//Expand; err[k] = Integrate[error[k]^2,{t,0,tmax}]/tmax; ]; (**********************************************************************************) (* Main Code *) (**********************************************************************************) ham[m0_,m1_]:=Module[{temp,k,n,C1}, For[k=Max[1,m0],k<=m1,k=k+1, Print[" k = ",k]; GetAll[k-1]; GetR[k]; RHS[k] = hbar*R[k]//Expand; Special = Linv[RHS[k]]; temp = Special + chi[k]*a[k-1]; C1 = -temp/.t->0; a[k] = temp + C1*Exp[-gamma*t]//Expand; A[k] = A[k-1] + a[k]//Expand; At[k] = D[A[k],t]; If[PRN == 1, GetErr[k,tmax]; Print[" error = ", err[k]//N]; ]; ]; Print["Successful !"]; ]; exact = 1/Sqrt[Q2/Q1-(Q2/Q1-1/a0^2)*Exp[-2*Q1*t]]; (* Input parameters *) a0 = 1; Q1 = 1; Q2 = 4;  P. G. SIDDHESHWAR Copyright © 2010 SciRes. AM 554 delta = 1/5; omega = 10; hbar = -1/2; gamma = 2*Q1; PRN = 0; tmax = 10; (* Print out the input parameters *) Print[" a0 = ",a0]; Print[" Q1 = ",Q1]; Print[" Q2 = ",Q2]; Print[" delta = ",delta]; Print[" omega = ",omega]; Print[" hbar = ",hbar]; (* get fifth-order approximation *) ham[1,5]; |

