Applied Mathematics, 2010, 1, 489-498
doi:10.4236/am.2010.16064 Published Online December 2010 (http://www.SciRP.org/journal/am)
Rotating Variable-Thickness Inhomogeneous Cylinders:
Part II—Viscoelastic Solutions and Applications
Ashraf M. Zenkour
Department of Mathematics, Faculty of Science, King AbdulAziz University, Jeddah, Saudi, Saudi Arabia
Department of Mathematics, Faculty of Science, Kafrelsheikh University, Kafr el-Sheikh, Egypt
Received June 2, 2010; revised October 12, 2010; accepted October 16, 2010
Abstract
Analytical solutions for the rotating variable-thickness inhomogeneous, orthotropic, hollow cylinders under
plane strain assumption are developed in Part I of this paper. The extensions of these solutions to the viscoe-
lastic case are discussed here. The method of effective moduli and Illyushin's approximation method are used
for this purpose. The rotating fiber-reinforced viscoelastic homogeneous isotropic hollow cylinders with uni-
form thickness are obtained as special cases of the studied problem. Numerical application examples are
given for the dimensionless displacement of and stresses in the different cylinders. The influences of time,
constitutive parameter and elastic properties on the stresses and displacement are investigated.
Keywords: Rotating, Viscoelastic Cylinder, Orthotropic, Variable Thickness and Density
1. Introduction
In recent years the subject of viscoelasticity has received
considerable attention from analysts and experimentalists.
The stress state of a viscoelastic hollow cylin der with the
help of internal pressure and temperature field is analyzed
in the literature [1,2]. A modified numerical method is
introduced by Ting and Tuan [3] to study the effect of
cyclic internal pressure on the stress and temperature
distributions in a viscoelastic cylinder. Talybly [4] has
investigated the state of stress and strain for a viscoelastic
hollow cylinder fastened to an elastic shell under non-
isothermal dynamic loading. Feng et al. [5] have obtained
the solution for finite d eformations of a viscoelastic solid
cylinder subjected to extension and torsion. The thermo-
mechanical behavior of a viscoelastic finite circular cylin-
der under axial harmonic deformations is presented by
Karnaukhov and Senc henk ov [6].
The determination of stress and displacement fields is
an important problem in design of engineering structures
using fiber-reinforced composite materials. The analyti-
cal solution for the rotating fiber-reinforced viscoelastic
cylinders becomes very complex when the thickness along
the radius of the cylinder is variable, even for simple
cases. Methods for solving quasi-static viscoelastic pro-
blems in composite structures have been developed by a
number of authors [7-9]. Allam and Appleby [10] have
used the realization method of elastic solutions to solve
the problem of bending of a viscoelastic plate reinforced
by unidirectionally elastic fibers. In other work [11], they
have used the method of effective moduli to determine
the stress concentrations around a circular hole or circu-
lar inclusion in a fiber-reinforced viscoelastic plate under
uniform shear. Allam and Zenkour [12] have used the
small parameter method as well as the method of
effective moduli for the bending response of a fiber-
reinforced viscoelastic arched bridg e model with quadra-
tic thickness variation and subjected to uniform loading.
In [13], they have also obtained the stresses around filled
and unfilled circular holes in a fiber-reinforced visco-
elastic plate under bending. The same author [14] have
developed closed form solutions for the rotating fiber-
reinforced viscoelastic solid and annular disks with
variable thickness by applying the generalization of
Illyushin's approximation method. In addition, Allam et
al. [15] have determined the stre ss concentrations aro und
a triangular hole in a fiber-reinforced viscoelastic com-
posite plate under uniform tension or pure bending. Also,
Zenkour et al. [16] have presented the elastic and visco-
elastic solutions to rotating functionally graded hollow
and solid cylinders.
In the present paper, the rotating fiber-reinforced
viscoelastic hollow cylinder is analytically studied. The
thickness of the cylinder and the elastic properties are

A. M. ZENKOUR
490
taken to be functions in the radial coordinate. The gove-
rning second-order differential equation is derived and
solved with the aid of some hypergeometric functions.
The displacement and stresses for rotating fiberrein-
forced viscoelastic inhomogeneous orthotropic hollow
cylinder with variable thickness and density subjected to
various boundary conditions are obtained. Special cases
of the studied problem are established and numerical
results are presented in graphical forms.
2. Rotation of Viscoelastic Cylinders
According to the elastic solution given in part I, we can
use the method of effective moduli and Illyushin's appro-
ximation method to solve the rotation problem of vari-
able thickness and density viscoelastic hollow cylinder
reinforced with unidirectionally elastic fibers.
For an orthotropic cylinder, the compliance parameters
ij

can be expressed in terms of the engineering cha-
racteristics as [17]:
 



11 22
12
13
23
11
=,=,
==,
==,
==,
rzz rz zr
rr zzrr zrz
rzrrzzrzr z
zrzr zzrrz
EE
EE
EE
EE
 
 
 
  
 

 

 











(1)
in which
=12 ,
rrzrrzz zr zrz   

    (2)
where i
E are Young's moduli and ij

are Poisson's
rations which are related by the reciprocal relations:
=, =,=.
rr zz rz zr
rrzz
EEEEEE




 
(3)
Now, consider a hollow cylinder made of a composite
material composed of two components. A viscoelastic
material as a first component, reinforced by unidirec-
tional elastic fibers as a second component. The first of
these components plays the ro le of filler and may posses
the properties of a linear viscoelastic material, and it is
described by the modulus
f
E and Poisson's ratio
f

.
The other component will be serve as the reinforcement
and is an elastic material with modulus of elasticity E
and Poisson's ratio

.
Under the above considerations and using the method
of effective moduli [14,18], Young's moduli and
Poisson's ratios, with 1 ====
rrrzz  

 and
2
==
zr z 

 , are given by [19]:
 

 
12
==, =1,
1
1
=,=1
11
f
rzf
f
ff
f
ff
E
E
EEE EE
EE
EE
EEEE



 

 
 




 

 

(4)
where

is the volume fraction of fiber reinforcement.
Thus, it is obvious that the reciprocal relations given in
Equation (3) are fulfilled.
Note that, the viscoelastic modulus
f
E is given by :
9
=,
2
fK
E


 (5)
where
K
is the coefficient of volume compression (the
bulk modulus) and it is assumed to be not relaxed, i.e.
=
K
const., and

is the dimensionless kernel of relaxa-
tion function which is related to the corresponding Poi-
sson's ratio by the form ula:
12
=.
1
f
f




 (6)
Substituting from Equations (5) and (6) into Equation
(4) yields



 

 
12
91
9
==,= ,
211 92
11 9
22 11
=,=
2 91 91
22
rz
p
p
EEEEE
p
p
pp




 
 
  

  


 



 

 




 
 
 







(7)
or in the simple form









21
2
11
1
11
21
9
==1,=911,
21
3
9111
2
=,
9119 11
3
=11,
2
rz
Ep
EEg EEpg
pgg
pgpg
g
 





 
 







 





 


 


(8)
in which
12
1119
=,=,=1,
1221
ii
p
g











(9)
where =/pKE is the constitutive parameter.
With the help of Equations (1) and (8), one can rewrite
the solutions given in Part I of this paper; see Equations
(20) and (23)-(25); in the form:


 
22
22
ˆ
=,,= ,,
ˆˆ
=,,=,,
rr rr
zz zz
uur r
rr
 
 

 




(10)
where

A. M. ZENKOUR
491
23
2222
00
ˆ
=,=.
bb
E
 

(11)
It is to be noted that, in elastic composites, the radial
displacement and stresses are functions of

and r
while in viscoelastic composites they are operator
functions of the time t and r. According to Illyushin's
approximation method [11,19,20], the function u can
be represented in the form:
 
5
=1
(, )=,
ii
i
urA r

 
 (12)
where ()
i

 are some known kernels, constructed on
the base of the kernel

and may be chosen in the
form:
12 345
12
1
=1, =,==, =,=,
g
g



 
(13)
where ,( =1,2)
i
gi

are given in Equation (9).
The coefficients ()
i
A
r are determined from the
system of algebraic equations

5
=1 =, =1,,5,
ij ji
j
LA Bi
 (14)
where

11
00
=,=,.
iji jii
LdBurd

  

(15)
Now, let us consider the relaxation function in an
exponential form

12
=,
t
tcce



 (16)
where 1 c and 2 c are constants to be experimentally
determined. Laplace-Carson transform can be used
to determine the functions ()t

and ()
i
g
t

. Denoting
the transforms of ()t

and ()
i
g
t

by ()t 
 and ()
i
g
t

,
since the transform of ()t

is
2
1
()= ,
s
c
scs 



(17)
thus, we get



 


/
2112
112
1/1
2112
112
1
=1, =,
1
=1
11
ccc
ccc
iii
iii
c
te t
ccc
c
gt e
ccc

 



















(18)
Equation (12) for a viscoelastic composite may be re-
corded to obtain explicit formula for the radial dis-
placement as function of r and time t in the form:
22
12
0
222
34
1 00
2
52
0
(,)= ()()()()()
()()()()()()
()( )().
t
tt
t
urtArt Artd
ArtdArgt d
Arg td


 

 

 
 




(19)
Taking 22
0
()= ()tHt, where ()
H
t is the Heaviside's
unit step function given by
10,
()= 0<0.
if t
Ht if t



 (20)
Then, Equation (19) takes the form

2
012 3 45
12
(,)=
()() ()()().
urt
A
Ht AtAt AgtAgt




(21)
wher e (), ()tt

 and ()
i
g
t

are given in Equations
(16) and (18). Using the same technique once again to
obtain the radial, circumferential and axial stresses for
the rotating fiber-reinforced viscoelastic hollow cylinder
with variable thickness and density by replacing only
(,)urt
 with (,)rt

 and making the suitable changes
in this case.
3. Applications
In this section, some numerical examples for the rotating
fiber-reinforced viscoelastic inhomogeneous variable-
thickness cylinder will be introduced. The results of the
present problem will be given for three sets of geometric
parameters k and n for the thickness profile. The nu-
merical applications will be carried out for the radial
displacement and stresses that being reported herein are
in the following dimensionless forms:
2222
0000
=,=,=,=.
ˆˆˆ
rr zz
rr z
u
u





 







The effect of the elastic properties of the cylinder,
constitutive and time parameters on the dimensionless
radial displacement and stresses will be shown. The cal-
culations will be carried out for the following values of
parameters: 12 =0.3,==0.1,=0.9cc

 and =0.5

.
In addition, other parameters are taken (except otherwise
stated) as:= 0.2,=2.5,=0.8pknand =1m. Also, the
coefficient

is still unknown and the time parameter
()t



is given in terms of it.
The distributions of the dimensionless stresses and
displacement through the radial direction of the rotating
fiber-reinforced viscoelastic inhomogeneous variable-
thickness cylinder are plotted in Figures 1-3 according
to the FF, CC, FC and CF boundary conditions,
respectively. For all hollow cylinders, the dimensionless
radial displacement r
u is the largest in the same
position for small k, i.e. =0.6k. For FF and CF
hollow cylinders, the dimensionless stresses are the
largest for small n. The minimum values of the dimen-
sionless radial stress r

at the outer surface of the CC
and FC hollow cylinders are larger for =0.6k. Also,

A. M. ZENKOUR 492
Figure 1. Dimensionless stresse s and displac eme nt for a var iable-thickness viscoelastic hollow cylinder subjected to various
boundary conditions (k = 0.6, n = 0.8, m = 0.5).

A. M. ZENKOUR
493
Figure 2. Dimensionless stresse s and displac eme nt for a var iable-thickness viscoelastic hollow cylinder subjected to various
boundary conditions (k = 2.5, n = 0.8, m = 0.5).
Figure 3. Dimensionless stresse s and displac eme nt for a var iable-thickness viscoelastic hollow cylinder subjected to various
boundary conditions (k = 2.5, n = 0.4, m = 0.5).

A. M. ZENKOUR 494
the dimensionless circumferential


and axial
z

stresses are smaller through the radial direction of the CC
hollow cylinders when =0.6k. The maximum value of


at the inner surface for FC hollow cylinder are the
smallest when k = 2.5 and n = 0.8. In addition, the di-
Figure 4. Distribution of dimensionless stresses and dis-
placement through the radial direction of a FF variable-
thickness viscoelastic hollow cylinder.
mensionless axial stresses are monotone decreasing in
r and it is smaller for n = 0.4 than for n = 0.8.
For a profile with geometric parameters =2.5k and
=0.8n, the dimensionless displacement and stresses are
plotted in Figures 4-7 for the rotating fiber-reinforced
Figure 5. Distribution of dimensionless stresses and dis-
placement through the radial direction of a CC variable-
thickness viscoelastic hollow cylinder.

A. M. ZENKOUR
495
Figure 6. Distribution of dimensionless stresses and dis-
placement through the radial direction of a FC variable-
thickness viscoelastic hollow cylinder.
viscoelastic inhomogeneous cylinder subjected to various
boundary conditions with different values of the para-
meter m. The stresses and displacement for =1m are
the smallest when compared to the results for =0m
Figure 7. Distribution of dimensionless stresses and dis-
placement through the radial direction of a CF variable-
thickness viscoelastic hollow cylinder.
and 1

. For FF and FC hollow cylinders, the dimen-
sionless radial displacement r u has changed concavity.
The dimensionless radial stress r

increases firstly to
get its maximum value then it decreases again at the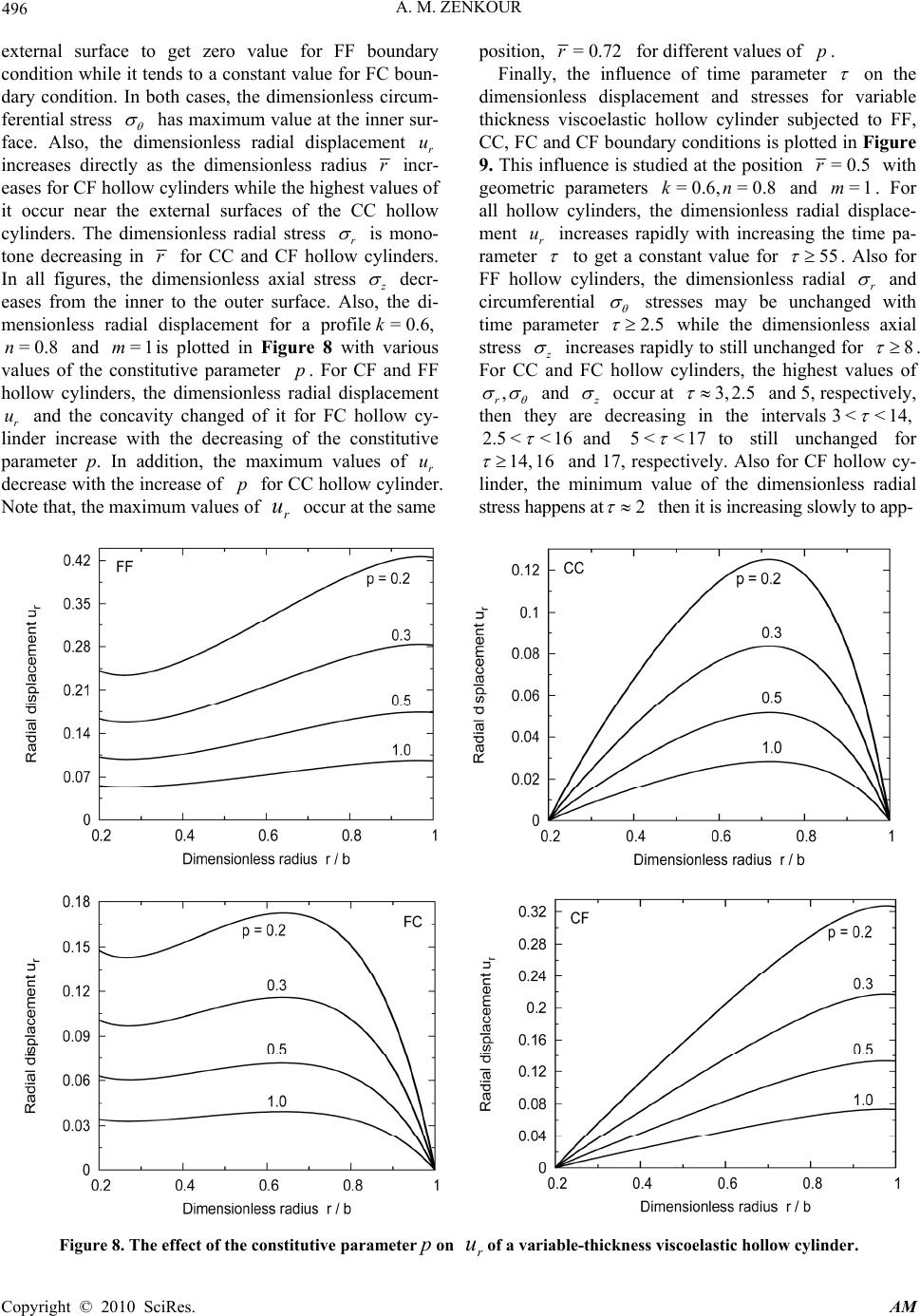

A. M. ZENKOUR
496
external surface to get zero value for FF boundary
condition while it tend s to a constant value for FC boun-
dary condition. In both cases, the dimensionless circum-
ferential stress


has maximum value at the inner sur-
face. Also, the dimensionless radial displacement r
u
increases directly as the dimensionless radius r incr-
eases for CF hollow cylinders while the h ighest values of
it occur near the external surfaces of the CC hollow
cylinders. The dimensionless radial stress r

is mono-
tone decreasing in r for CC and CF hollow cylinders.
In all figures, the dimensionless axial stress
z

decr-
eases from the inner to the outer surface. Also, the di-
mensionless radial displacement for a profile=0.6,k
=0.8n and =1mis plotted in Figure 8 with various
values of the constitutive parameter p. For CF and FF
hollow cylinders, the dimensionless radial displacement
r
u and the concavity changed of it for FC hollow cy-
linder increase with the decreasing of the constitutive
parameter p. In addition, the maximum values of r
u
decrease with the increase of p for CC hollow cylinder.
Note that, the maximum values of r
u occur at the same
position, =0.72r for different values of p.
Finally, the influence of time parameter

on the
dimensionless displacement and stresses for variable
thickness viscoelastic hollow cylinder subjected to FF,
CC, FC and CF boundary condition s is plotted in Figure
9. This influence is studied at the position =0.5r with
geometric parameters =0.6, =0.8kn
and =1m. For
all hollow cylinders, the dimensionless radial displace-
ment r
u increases rapidly with increasing the time pa-
rameter

to get a constant value for 55

. Also for
FF hollow cylinders, the dimensionless radial r

and
circumferential


stresses may be unchanged with
time parameter 2.5

 while the dimensionless axial
stress
z

increases rapidly to still un changed for 8

.
For CC and FC hollow cylinders, the highest values of
,
r


 and
z

occur at 3,2.5

 and 5, respectively,
then they are decreasing in the intervals3 <<14,

2.5 <<16

and 5< <17

to still unchanged for
14,16

 and 17, respectively. Also for CF hollow cy-
linder, the minimum value of the dimensionless radial
stress happens at2


then it is increasing slowly to app-
Figure 8. The effect of the constitutive parameter p on r uof a variable-thickness viscoelastic hollow cylinder.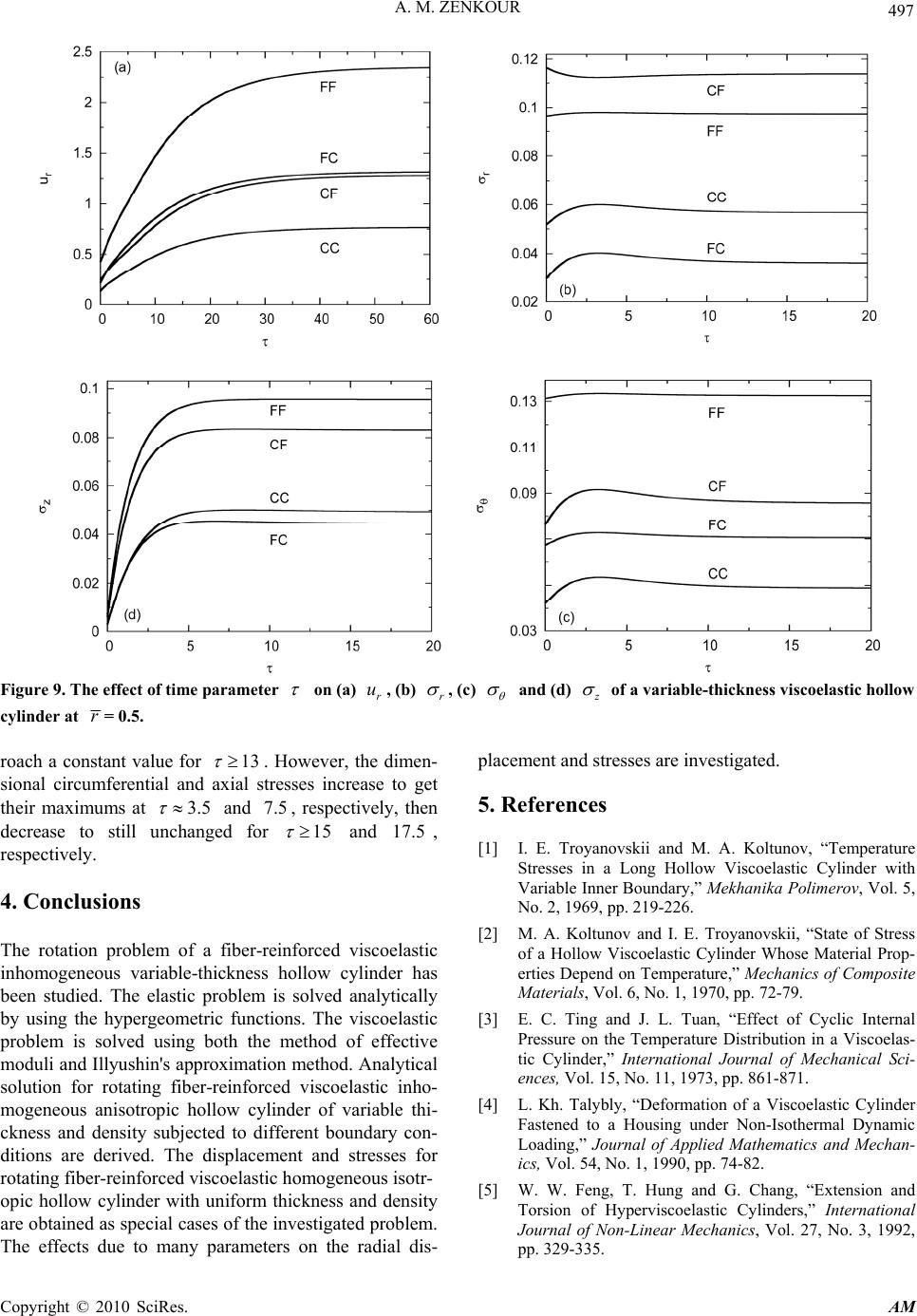

A. M. ZENKOUR
497
Figure 9. The effect of time parameter

on (a) r u, (b) r

, (c)


and (d)
z

of a variable-thickness viscoelastic hollow
cylinder at r= 0.5.
roach a constant value for 13

. However, the dimen-
sional circumferential and axial stresses increase to get
their maximums at 3.5

 and 7.5 , respectively, then
decrease to still unchanged for 15

 and 17.5 ,
respectively.
4. Conclusions
The rotation problem of a fiber-reinforced viscoelastic
inhomogeneous variable-thickness hollow cylinder has
been studied. The elastic problem is solved analytically
by using the hypergeometric functions. The viscoelastic
problem is solved using both the method of effective
moduli and Illyushin's approximation method. Analytical
solution for rotating fiber-reinforced viscoelastic inho-
mogeneous anisotropic hollow cylinder of variable thi-
ckness and density subjected to different boundary con-
ditions are derived. The displacement and stresses for
rotating fiber-reinforced viscoelastic homogeneous isotr-
opic hollow cylinder with uniform thickness and density
are obtained as special cases of the investigated problem.
The effects due to many parameters on the radial dis-
placement and stresses are investigated.
5. References
[1] I. E. Troyanovskii and M. A. Koltunov, “Temperature
Stresses in a Long Hollow Viscoelastic Cylinder with
Variable Inner Boundary,” Mekhanika Polimerov, Vol. 5,
No. 2, 1969, pp. 219-226.
[2] M. A. Koltunov and I. E. Troyanovskii, “State of Stress
of a Hollow Viscoelastic Cylinder Whose Material Prop-
erties Depend on Temperature,” Mechanics of Composite
Materials, Vol. 6, No. 1, 1970, pp. 72-79.
[3] E. C. Ting and J. L. Tuan, “Effect of Cyclic Internal
Pressure on the Temperature Distribution in a Viscoelas-
tic Cylinder,” International Journal of Mechanical Sci-
ences, Vol. 15, No. 11, 1973, pp. 861-871.
[4] L. Kh. Talybly, “Deformation of a Viscoelastic Cylinder
Fastened to a Housing under Non-Isothermal Dynamic
Loading,” Journal of Applied Mathematics and Mechan-
ics, Vol. 54, No. 1, 1990, pp. 74-82.
[5] W. W. Feng, T. Hung and G. Chang, “Extension and
Torsion of Hyperviscoelastic Cylinders,” International
Journal of Non-Linear Mechanics, Vol. 27, No. 3, 1992,
pp. 329-335.

A. M. ZENKOUR
498
[6] V. G. Karnaukhov and I. K. Senchenkov, “Thermome-
Chanical Behavior of a Viscoelastic Finite Circular Cy-
linder under Harmonic Deformations,” Journal of Engi-
neering Mathematics, Vol. 46, No. 3-4, 2003, pp.
299-312.
[7] D. Bland, “The Linear Theory of Viscoelasticity,” Per-
gamon Press, New York, 1960.
[8] D. Abolinsh, “Elasticity Tensor for Unidirectionally
Reinforced Elastic Material,” Polymer Mechanics, Vol. 4,
No. 1, 1965, pp. 25-59.
[9] A. A. Illyushin and B. E. Pobedria, “Foundations of Ma-
thematical Theory of Thermo-Viscoelasticity,” in Russian,
Nauka, Moscow, 1970.
[10] M. N. M. Allam and P. G. Appleby, “On the Plane De-
formation of Fiber-Reinforced Viscoelastic Plates,” Ap-
plied Mathematical Modelling, Vol. 9, No. 5, 1985, pp.
341-346.
[11] M. N. M. Allam and P. G. Appleby, “On the Stress Con-
centrations around a Circular Hole in a Fiber-Reinforced
Viscoelastic Plate,” Res Mechanica, Vol. 19, No. 2, 1986,
pp. 113-126.
[12] M. N. M. Allam and A. M. Zenkour, “Bending Response
of a Fiber-Reinforced Viscoelastic Arched Bridge Mod-
el,” Applied Mathematical Modelling, Vol. 27, No. 3,
2003, pp. 233-248.
[13] A. M. Zenkour and M. N. M. Allam, “Stresses around
Filled and Unfilled Circular Holes in a Fiber-Reinforced
Viscoelastic Plate under Bending,” Mechanics of Ad-
vanced Materials and Structures, Vol. 12, No. 6, 2005,
pp. 379-389.
[14] A. M. Zenkour and M. N. M. Allam, “On the Rotating
Fiber-Reinforced Viscoelastic Composite Solid and An-
nular Disks of Variable Thickness,” International Journal
for Computational Methods in Engineering Science and
Mechanics, Vol. 7, No. 1, 2006, pp. 21-31.
[15] M. N. M. Allam, A. M. Zenkour and H. F. El-Mekawy,
“Stress Concentrations in a Viscoelastic Composite Plate
Weakened by a Triangular Hole,” Composite Structures,
Vol. 79, No. 1, 2007, pp. 1-11.
[16] A. M. Zenkour, K. A. Elsibai and D. S. Mashat, “Elastic
and Viscoelastic Solutions to Rotating Functionally
Graded Hollow and Solid Cylinders,” Applied Mathe-
matics and Mechanics - English Edition, Vol. 29, No. 12,
2008, pp. 1601-1616.
[17] A. E. Bogdanovich and C. M Pastore, “Mechanics of
Textile and Laminated Composites with Applications to
Structural Analysis,” Chapman and Hall, New York,
1996.
[18] B. E. Pobedria, “Structural Anisotropy in Viscoelastici-
ty,” Mechanics of Composite Materials, Vol. 12, No. 4,
1976, pp. 557-561.
[19] A. M. Zenkour, “Thermal Effects on the Bending Re-
sponse of Fiber-Reinforced Viscoelastic Composite Pla-
tes using a Sinusoidal Shear Deformation Theory,” Acta
Mechanica, Vol. 171, No. 3-4, 2004, pp. 171-187.
[20] M. N. M. Allam and B. E. Pobedria, “On the Solution of
Quasi-Statical Problems of Anisotropic Viscoelasticity,”
Izv. Acad. Nauk ArSSR, In Russian, Mechanics, Vol. 31,
No. 1, 1978, pp. 19-27.