Applied Mathematics, 2010, 1, 481-488
doi:10.4236/am.2010.16063 Published Online December 2010 (http://www.SciRP.org/journal/am)
Rotating Variable-Thickness Inhomogeneous
Cylinders: Part I—Analytical Elastic Solutions
Ashraf M. Zenkour
Department of Mathematics, Faculty of Science, King AbdulAziz University, Jeddah, Saudi Arabia
Department of Mathematics, Faculty of Science, Kafrelsheikh University, Egypt
Received June 2, 2010; revised December 12, 2010; accepted December 16, 2010
Abstract
In this paper, an analytical solution for the rotation problem of an inhomogeneous hollow cylinder with
variable thickness under plane strain assumption is developed. The present cylinder is made of a fiber-
reinforced viscoelastic inhomogeneous orthotropic material. The thickness of the cylinder is taken as
parabolic function in the radial direction. The elastic properties varies in the same manner as the thickness of
the cylinder while the density varies according to an exponential law form. The inner and outer surfaces of
the cylinder are considered to have combinations of free and clamped boundary conditions. Analytical
solutions are given according to different types of the hollow cylinders. An extension of the present solutions
to the viscoelastic ones and some applications are investigated in Part II.
Keywords: Rotating, Inhomogeneous Cylinders, Orthotropic, Variable Thickness and Density
1. Introduction
The rotation problem of inhomogeneous cylinder has
been important applications, particularly in mechanical
engineering, aerospace industry, underwater vehicles and
biomechanics. The pertinent literature on the investiga
tion of stresses and displacements in an inhomogeneous
hollow circular cylinder may be reviewed here. The plane
strain problem of a rotating inhomogeneous orthotropic
hollow cylinder is solved by Senitskii [1]. Horgan and
Chan [2] analyzed two-dimensional plane stress/strain
deformations by assuming Youngs modulus to be a power
law function of the radial direction of the cylinder and
constant Poisson's ratio. Vasilenko and Klimenko, [3]
have analyzed the stress state of a rotating cylinder,
inhomogeneous in the radial direction, having one plane
of elastic symmetry and loaded with centrifugal forces.
Rooney and Ferrari [4] have examined the tension, ben-
ding, and flexure of cylinders with functionally graded
(FG) cross-section. The effect of inhomogeneity of elastic
properties and density in the circumferential direction on
the distribution of stress and displacement in orthotropic
cylindrical panels using load in the axial direction is
investigated by Grigorenko and Vasilenko [5]. Oral and
Anlas [6] have analyzed the effect of continuous in-
homogeneity on the stress distribution in an anisotropic
cylinder. Pan and Roy [7] have solved a plane-strain
problem for a FG cylinder by dividing it into several
homogeneous cylinders. Tutuncu [8] has gave the power
series solution for stresses and displacements in FG
cylinders with exponentially-varying elastic modulus
through the radial direction. Theotokoglou and Stam-
pouloglou [9] have studied axisymmetric problems for
radially inhomogeneous circular cylinders. The effect of
varying Poisson's ratio on deformation fields in FG
cylinders has been investigated by Mohammadi and
Dryden [10]. Li and Peng [11] have analyzed axisy-
mmetric deformations of FG hollow cylinders and disks
with arbitrarily varying material properties.
In recent years considerable attention has been given
to solutions for the cylinders with variable thickness.
Variable-thickness hollow cylinder is a common struc-
ture type which can be used in some applications in-
volving aerospace, submarine structures, nuclear reactors
as well as chemical pipes. Grigorenko and Rozhok [12]
have studied the stress problem for non-circular hollow
cylinder with variable thickness under uniform and local
loads. Zenkour [13] has established the stresses in a
rotating variable-thickness orthotropic cylinder cont-
aining a solid core of uniform-thickness. Also, Zenkour
[14] has analytically investigated the behavior of com-
posite circular cylinders subjected to internal and ex-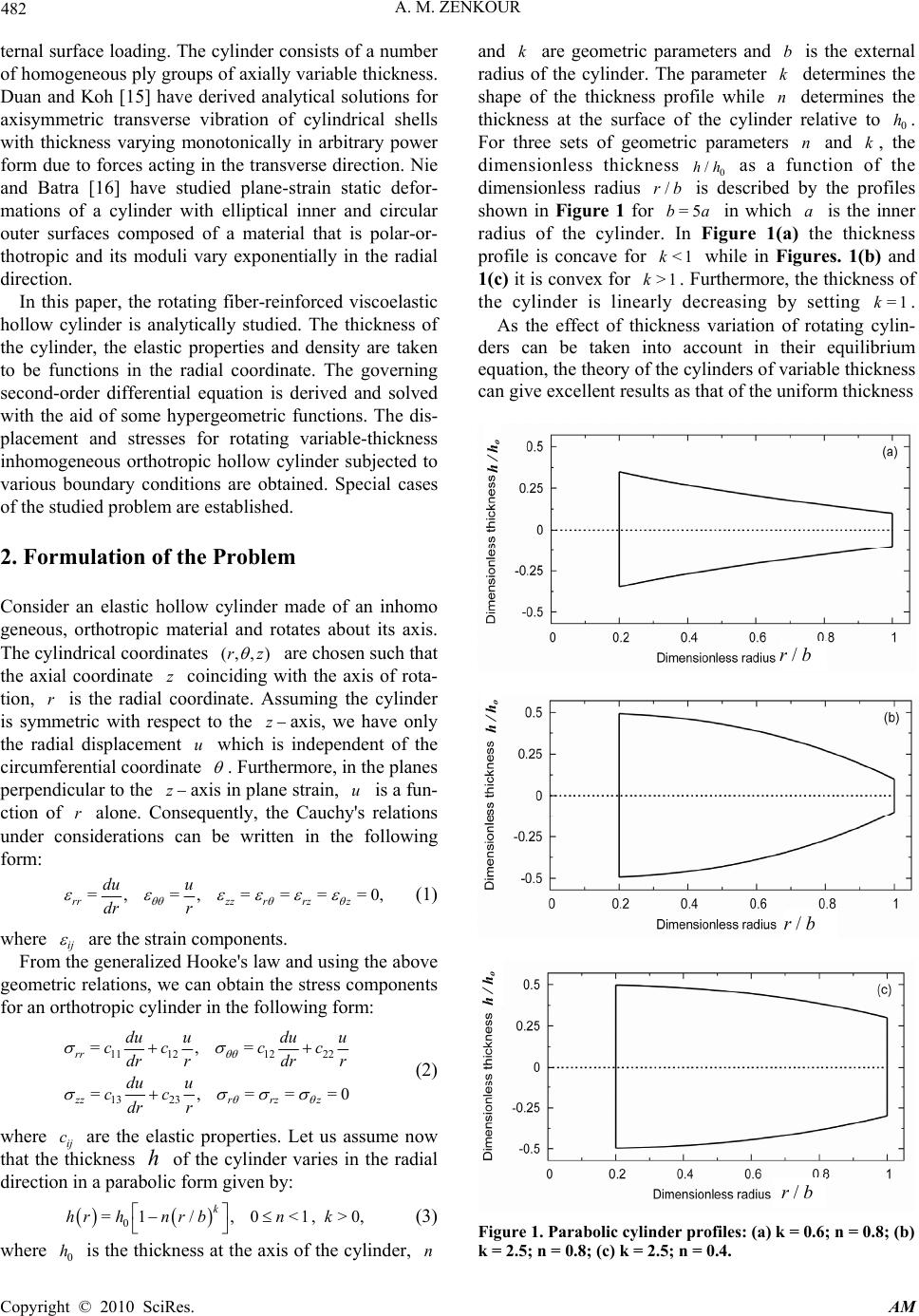

A. M. ZENKOUR
482
ternal surface loading. The cylinder consists of a number
of homogeneous ply groups of axially variable thickness.
Duan and Koh [15] have derived analytical solutions for
axisymmetric transverse vibration of cylindrical shells
with thickness varying monotonically in arbitrary power
form due to forces acting in the transverse direction. Nie
and Batra [16] have studied plane-strain static defor-
mations of a cylinder with elliptical inner and circular
outer surfaces composed of a material that is polar-or-
thotropic and its moduli vary exponentially in the radial
direction.
In this paper, the rotating fiber-reinforced viscoelastic
hollow cylinder is analytically studied. The thickness of
the cylinder, the elastic properties and density are taken
to be functions in the radial coordinate. The governing
second-order differential equation is derived and solved
with the aid of some hypergeometric functions. The dis-
placement and stresses for rotating variable-thickness
inhomogeneous orthotropic hollow cylinder subjected to
various boundary conditions are obtained. Special cases
of the studied problem are established.
2. Formulation of the Problem
Consider an elastic hollow cylinder made of an inhomo
geneous, orthotropic material and rotates about its axis.
The cylindrical coordinates (, ,)rz

are chosen su ch th a t
the axial coordinate z coinciding with the axis of rota-
tion, r is the radial coordinate. Assuming the cylinder
is symmetric with respect to the zaxis, we have only
the radial displacement u which is independent of the
circumferential coordinate

. Furthermore, in the planes
perpendicular to the zaxis in plane strain, u is a fun-
ction of r alone. Consequently, the Cauchy's relations
under considerations can be written in the following
form:
=,=,= == =0,
rrzz rrzz
du u
dr r
 

(1)
where ij

are the strain components.
From the generalized Hooke's law and using the above
geometric relations, we can obtain the stress components
for an orthotropic cylinder in the following form:
11 121222
13 23
=,=
=,===0
rr
zzr rz z
du uduu
cc cc
dr rdrr
du u
cc
dr r






(2)
where ij
c are the elastic properties. Let us assume now
that the thickness h of the cylinder varies in the radial
direction in a parabolic form given by:
 
0
=1/,0 <1,>0,
k
hrhnr bnk


 (3)
where 0 h is the thick ness at the axis of the cylinder, n
and k are geometric parameters and b is the external
radius of the cylinder. The parameter k determines the
shape of the thickness profile while n determines the
thickness at the surface of the cylinder relative to 0
h.
For three sets of geometric parameters n and k, the
dimensionless thickness 0 /hh as a function of the
dimensionless radius /rb is described by the profiles
shown in Figure 1 for =5ba in which a is the inner
radius of the cylinder. In Figure 1(a) the thickness
profile is concave for <1k while in Figures. 1(b) and
1(c) it is conv ex for >1k. Furthermore, the thickness of
the cylinder is linearly decreasing by setting =1k.
As the effect of thickness variation of rotating cylin-
ders can be taken into account in their equilibrium
equation, the theory of the cylin d ers of variable th ickness
can give excellent results as that of the uniform thickness
Figure 1. Parabolic cylinder profiles: (a) k = 0.6; n = 0.8; (b)
k = 2.5; n = 0.8; (c) k = 2.5; n = 0.4.
h / ho
h / ho
h / ho
r / b
r / b
r / b

A. M. ZENKOUR
483
cylinders as long as they meet the assumption of plane
strain. After considering this effect, the equilibrium
equation of rotating cylinder with variable thickness can
be written as:

22
=0,
rr
dhrhh r
dr

  (4)
where  is the constant angular velocity and

is the
density of the cylinder material.
We characterize the elastic properties ij c and the ma-
terial density

of inhomogeneous cylinder by:


/
0
=1/ ,=,
k
kmrb
ij ij
cnrb e 



 (5)
where ij

and 0

are the values of ij c and

in the
homogeneous case, respectively, and m is a rational
number.
3. Elastic Solution
Substituting from Equation (2) into Equation (4) with the
aid of the expressions given in Equation (5) and the
cylinder profile given in Equation (3), we can get the
following confluent hypergeometric differential equation
for the radial displacement ()ur :
23 (/)2
22 0
211
2 (/)2(/)
1=0,
1(/)1(/) 1(/)
k
mr bkk
kk
k
red unk rbdunk rb
rr u
dr
drn rbn rbnr b



 

 
 



 

(6)
where
22 1112 11
=/,=/.

 (7)
Introducing the dimensionless radius =/rrb in
Equation (6), then its general solution can be written as
(1/2/ )(1/2/ )
112 2
ˆˆ
()=()() (),
kk
urnCPrnCP rRr
 
 (8)
where 1
ˆ
C and 2
ˆ
C are arbitrary integration constants and





()
1
()
2
=,,,,
=1,1,2,,
k
k
Prr Mijnr
Pr r Mijnr




   (9)
in which
22
2
=1,=1,=1,=2 .
ij kk
kkk
 




  (10)
Note that, the function (,, ,)
M
z

 is the generalized
hypergeometric function defined by [17]:
=0
(,, ,)=,=,
!
q
qq k
q
q
z
M
zznr
q

 

 (11)
where q

, for example, is the Pochhammer's symbol
given by ()
=(1)(2)(1)=,
()
qq
q

 

   (12)
in which  represents Gamma function. It is to be
noted that, for real values of the upper parameters

and

, and non-zero real value of the lower parameter

the generalized hypergeometric function (,, ,)
M
z


converges for ||<1z.
The particular solution ()
R
rfor Equation (8) is
obtaine d u sing vari ation of parame t e r s as
112 2
()=() ()()(),
R
rU rPrUrPr (13)
where
21
12
00
()() ()()
()=, ()=,
() ()
rr
Pf Pf
UrdUrd
 





(14)
in which

23
0
11
()= ,
1
k
mr
k
bre
fr nr




 (15)
and ()r

is the Wronskian given by
21
12
() ()
()= ()().
dPrdP r
rPrPr
dr dr

(16)
Therefore,


 



 


22
23 21
012
00
11
= ,
11
kk
mm
rr
kk
eM eM
b
RrrM rdrMrd
nF nF
 

 



 
 








(17)
where


 


21
12 12
=2.
dMrdM r
FrrM rMrMrMr
dr dr





(18)
Note that, the first derivative of the general hypergeo-
metric function is given by:
 
, ,,=1,1,1,.
ddz
M
zM z
dr dr

  

 (19)

A. M. ZENKOUR
484
Consequently, the exact general solution for the radial
displacement can be written as


 

 
1112 22
=,urrMrCF rrMrCFr
 
 
 
(20)
where
 
1/2 /1/2 /
112 2
ˆˆ
=,=,
kk
Cn CCn C
 
(21)
and
 


 


2
23 2
0
10
11
2
23 1
0
20
11
=,
1
=.
1
k
m
r
k
k
m
r
k
eM
b
Fr d
nF
eM
b
Fr d
nF


















(22)
Substituting from Equation (20) into Equation (2)
yields the radial, circumferential and axial stresses for
the rotating variable thickness and density inhomogen-
eous orthotropic hollow cylinder in the following form:



   
()
111 222
1111111211 122111112112
=
1
rr
k
r
nrdMM dFdMMdF
rCFMr CFM
bdrr drdrrdr


 

 
  
 
   
 
 
 
 
(23)

 
() () 111222
1112122212122121222122
=
1()( )
k
r
nrdMM dFdMMdF
rCFMr CFM
bdrrdrdrrdr

 

 

 
  
 
   
 
 
 
 
(24)







() 111222
1113132313 122131323132
=
1.
zz
k
r
nrdMM dFdMMdF
rCFMr CFM
bdrrdrdrrdr



 


 
 
 
 

 
 
 


(25)
Note that, if ==0nm then 00
()= ,=, =
ij ij
hrhc


and the radial displacement given in Equation (20) for
the rotating uniform thickness and density homogeneous
orthotropic hollow cylinder is reduced to

 

233
0
12 2
11
=,
9
br
ur CrCr




 (26)
also, the corresponding stresses in this case are given by:
 




 




 




11
222
11 12
111 12211 120
2
11
11 222
12 22
111 22212220
2
11
11 222
13 23
113 23213 230
2
11
13
=,
9
13
=,
9
31
=.
9
rr
zz
rC rCrbr
b
rC rCrbr
b
rC rCrbr
b





 


 


 






 




 




 


(27)
In addition, for isotropic cylinder we have [18]


 
11 2212 1323
1
== ,=== ,
112 112
EE 
 



 
(28)
where E and

are Young's modulus and Poisson's
ratio of the cylinder material. Using Equation (28) we
find that the solution given in Equations (26) and (27) for
the rotating uniform thickness and density homogeneous
isotropic hollow cylinder takes the form:






 


 


 
 

233 2
10
222
12 0
2
222
12 0
2
232
10
112
=,
81
12 32
=,
112 81
12 12
=,
112 81
112
2
=.
112 41
rr
zz
C
ur Crbr
rE
E
rCC br
br
E
rCC br
br
E
rC br
bE









 



 

 




 




 





 


(29)

A. M. ZENKOUR
485
The previous elastic solutions will be completed by
calculating the integration constantsi Cusing various bo-
undary conditions on the surfaces of the hollow cylinder.
4. Rotation of Elastic Hollow Cylinders
In the present section, we will obtain the elastic so lutions
for the rotating hollow cylinder. For the present hollow
cylinder, the solution requires that one boundary con-
dition be satisfied at each surface. The radial stress must
be vanished at the free surface (F) of the cylinder while
the radial displacement must be equal to zero at the
clamped surface (C) of the cylinder.
4.1. Free-Free (FF) Hollow Cylinder
When the inner and outer surfaces (=,=rarb or
=/=,=1)rabar of the cylinder are free of any traction,
the boundary conditions are given by:



=0= ,
=0 =1.
rr
rr
ratra
ratr


(30)
Using the above conditions into Equation (23), the
constants 1 C and 2 C are given by
  
  
12122223 121112121322
111 221221
111 212 1321121 2222311
211 221221
11
=,
11
=,
FS FSSSFaSFaSSS
CSS SS
FaSFaSS SFSFSSS
CSS SS
 
 

 


(31)
where

 


1
111111112
=
M
a
Sa Maa







 


2
1211 21112
=
M
a
Sa Maa







 

 
13 111122
=SaMaFaaMaFa




 

(32)






2111 111121
=1 1SMM 







2211211122
=1 1SM M 









2311 1122
=1111SMFMF 

 

in which the prime ()
 means differentiation with
respect to r.
The radial displacement and stresses for the rotating
variable thickness and density inhomogeneous orthotro-
pic hollow cylinder with free surfaces can be calculated
from Equations (20), (23)-(25) and (32).
The solution given in Equations (26) and (27) for the
rotating uniform thickness and density homogeneous
orthotropic hollow cylinder with free surfaces can be
obtained with the help of the following constants:




 




 
3223
11 120
111
2
111112
3223
11 120
211
2
111112
31
=,
9
31
=9
aab
Caa
aab
Caa




 
 
 









 





 

(33)
Also, the radial displacement and stresses given in
Equation (29) for the rotating uniform thickness and
density homogeneous isotropic hollow cylinder with free
surfaces can be written as
 



2
2223
0
2
112 32
=132
81 12
a
urar br
Er
 



 
 



 
2
2222
0
2
32
=1
81
rr a
rarb
r




 


 
2
2222
0
2
32 12
=1
813 2
a
rarb
r






 



(34)
 



2222
0
=1322
41
zz rarb








A. M. ZENKOUR 486
This is the well-known solution of the rotating uni-
form thickness cylinder [19].
4.2. Clamped-Clamped (CC) Hollow Cylinder
When the inner and outer surfaces


=,=1rar of the
cylinder are clamped, the boundary conditions are given
by:



=0= ,
=0 =1.
urat ra
urat r (35)
From these conditions and Equation (20), the con-
stants 1
C and 2 C are given by
 










 
  
 
112241114241 2
1214141
1142 411112214
2214141
11 111
=,
11
11111
=,
11
MFMF S FaSFaSM
CMSMS
FaSFaS MMFMFS
CMSMS
 


 


(36)
where




141 412
=,= .SaMaSaMa
  (37)
With the h elp of Equation s (2 0), ( 23)-(25) and(36) ,w e
can obtain the radial displacement and stresses for the
rotating variable thickness and density inhomogeneous
orthotropic hollow cylinder with clamped surfaces.
The solution given in Equation (27) for the rotating
uniform thickness and density homogeneous orthotropic
hollow cylinder with clamped surfaces can be calculated
with the aid of the following co nstants:


 


 
33
323 323
00
12
22
11 11
11
=,=.
99
aab aab
CC
aa aa

 

 
 

 
 
 


 


(38)
Finally, the radial displacement and stresses given in
Equation (29) for the rotating uniform thickness and
density homogeneous isotropic hollow cylinder with
clamped surfaces becomes
  

 


 


 
2
2223
0
2
2
22 22
02
2
22 22
02
22 22
0
112
=1 ,
81
12
=1 32,
81
12
=1 12,
81
=12 .
41
rr
zz
a
urar br
Er
a
b
rar
r
a
b
ra r
r
rarb

 













  





 



















 


(39)
4.3. Free-Clamped (FC) Hollow Cylinder
When the inner surface of the cylinder

1=Cr a is
free of any traction and the outer surface


=1r is
clamped, the boundary conditions are given by:



=0= ,
=0 =1.
rr ratra
urat r

(40)
From Equations (40), (20) and (23), the constants 1
C
and 2
C are given by














 
  

112212111212 132
1211112
111 212 13 1112211
2211112
11 111
=,
11
111(1)1
=.
11
MFMF S FaSFaSSM
CMSMS
FaSFaSS MMFMFS
CMSMS
 


 


(41)
Substituting from these constants into Equations (20),
(23)-(25), we can get the radial displacement and stresses
for the rotating variable thickness and density inhomo-
geneous orthotropic hollow cylinder with free inner and
clamped outer surfaces.
In addition, the solution for the rotating uniform
thickness and density homogeneous orthotropic hollow
cylinder with free inner and clamped outer surfaces can
be obtained from Equations (26) and (27) with the help
of the following constants:

A. M. ZENKOUR
487


















3223
11 1211 120
111
2
1111 1211 12
3223
11 1211 120
211
2
1111 121112
3
=9
3
=9
aab
Caa
aab
Caa




  
  
  
  





 


 


 


 

(42)
Also, the radial displacement and stresses given in
Equation (29) for the rotating uniform thickness and
density homogeneous isotropic hollow cylinder with free
inner and clamped outer surfaces can be obtained in the
following form:
  

 
 
 

 
 
42
2223
0
223
42 2
22 2
0222
42 2
22
022
11212321 32
=,
81 12 12
1232132 12
=32,
81 12 12
1232132 12
=811212
rr
aa
a
urr br
Eaar
aa a
b
rr
aar
aa a
b
raa

 

 



 



  


 



  


 


  

 

 

2
2
4222
0
2
12 ,
12 32
=2.
41 12
zz
r
r
a
rrb
a











 




(43)
4.4. Clamped-Free (CF) Hollow Cylinder
When the inner surface of the cylinder


=ra is
clamped and the outer surface


=1r is free of any
traction, the bound ary conditions are given by:



=0= ,
=0 =1.
rr
urat ra
ratr 
(44)
From Equations (20), (23) and (44), the constants 1
C
and 2 C are given by
  
 
1212222341114241 22
1221421 41
114 24121121222 2314
222 1421 41
11
=,
11
=
FS FS SSFaS FaSS
CSSSS
FaSFaS SFSFSS S
CSS SS
 



 

(45)
The radial displacement and stresses for the rotating
variable thickness and density inhomogeneous orthotr-
opic hollow cylinder with clamped inner and free outer
surfaces can be obtained from Equations (20), (23)-(25)
and (45).
Also, the solution given in Equation (27) for the
rotating uniform thickness and density homogeneous
orthotropic hollow cylinder with clamped inner and free
outer surfaces can be calculated with the help of the
following constants:

















3323
11 1211120
12
11111211 12
3323
11 1211 120
22
11111211 12
3
=,
9
3
=.
9
aab
Caa
aab
Caa




 
  
 
 





 














(46)
Finally, one can obtain easily the radial displacement
and stresses given in Equation (29) for the rotating
uniform thickne ss and densit y hom ogeneous is otropic hollow
cylinder with clamped inner and free outer surfaces in the
following form:
  


 


 
 
422 223
0
223
42
22 22
0222
42
22 2
0222
11232 12
32
=,
81 12 12
32 1212
32
=32,
81 12 12
32 1212
32
=8112 12
rr
aaa
urr br
Eaar
aa
ba
rr
aar
aa
ba
raar

 

 



 



 


 



 



 


 


 

 

2
4222
0
2
12 ,
32 12
=2.
41 12
zz
r
a
rrb
a











 




(47)

A. M. ZENKOUR 488
5. Conclusions
The rotation problem of a variable-thickness inhomogen-
eous, orthotropic, hollow cylinder has been studied.
Analytical solution for rotating variable-thickness, in-
homogeneous, orthotropic, hollow cylinder subjected to
different boundary conditions are derived. The displace-
ment and stresses for rotating uniform-thickness, homo-
geneous, isotropic, hollow cylinder are obtained as
special cases of the investigated problem. In the second
part of this paper we will present the corresponding
viscoelastic solutions and some applications concerning
the effects due to many parameters on the radial displace-
ment and stresses.
6. References
[1] Yu. É. Senitskii, “Stress State of a Rotating Inhomoge-
neous Anisotropic Cylinder of Variable Density,” Inter-
national Applied Mechanics, Vol. 28, No. 5, 1992, pp.
28-35.
[2] C. O. Horgan and A. M. Chan, “The Pressurized Hollow
Cylinder or Disk Problem for Functionally Graded Iso-
tropic Linear Elastic Materials,” Journal of Elasticity,
Vol. 55, No. 1, 1999, pp. 43-59.
[3] A. T. Vasilenko and N. I. Klimenko, “Stress State of
Rotating Inhomogeneous Anisotropic Cylinders,” Inter-
national Applied Mechanics, Vol. 35, No. 8, 1999, pp.
778-783.
[4] F. Rooney and M. Ferrari, “Tension, Bending, and Flex-
ure of Functionally Graded Cylinders,” International
Journal of Solids and Structures, Vol. 38, No. 3, 2001, pp.
413-421.
[5] Ya. M. Grigorenko and A. T. Vasilenko, “The Effect of
Inhomogeneity of Elastic Properties on the Stress State in
Composite Cylindrical Panels,” Mechanics of Composite
Materials, Vol. 37, No. 2, 2001, pp. 85-90.
[6] A. Oral and G. Anlas, “Effects of Radially Varying Mod-
uli on Stress Distribution of Nonhomogeneous Aniso-
tropic Cylindrical Bodies,” International Journal of Sol-
ids and Structures, Vol. 42, No. 20, 2005, pp. 5568-5588.
[7] E. Pan and A. K. Roy, “A Simple Plane-strain Solution
for Functionally Graded Multilayered Isotropic Cylind-
ers,” Structural Engineering and Mechanics, Vol. 24, No.
6, 2006, pp. 727-740.
[8] N. Tutuncu, “Stresses in Thick-walled FGM Cylinders
with Exponentially-varying Properties,” Engineering
Structures, Vol. 29, No. 9, 2007, pp. 2032-2035.
[9] E. E. Theotokoglou and I. H. Stampouloglou, “The Ra-
dially Nonhomogeneous Elastic Axisymmentric Prob-
lem,” International Journal of Solids and Structures, Vol.
45, No. 25-26, 2008, pp. 6535-6552.
[10] M. Mohammadi and J. R. Dryden, “Influence of the Spa-
tial Variation of Poisson’s Ratio upon the Elastic Field in
Nonhomogeneous Axisymmetric Bodies,” International
Journal of Solids and Structures, Vol. 46, No. 3-4, 2009,
pp. 788-795.
[11] X. F. Li and X. L. Peng, “A Pressurized Functionally
Graded Hollow Cylinder with Arbitrarily Varying Ma-
terial Properties,” Journal of Elasticity, Vol. 96, No. 1,
2009, pp. 81-95.
[12] Ya. M. Grigorenko and L. S. Rozhok, “Stress Analysis of
Hollow Elliptic Cylinders with Variable Eccentricity and
Thickness,” International Applied Mechanics, Vol. 38,
No. 8, 2002, pp. 954-966.
[13] A. M. Zenkour, “Rotating Variable-thickness Orthotropic
Cylinder Containing a Solid Core of Uniform-thickness,”
Archive of Applied Mechanics, Vol. 76, No. 1-2, 2006, pp.
89-102.
[14] A. M. Zenkour, “Stresses in Cross-ply Laminated Circu-
lar Cylinders of Axially Variable Thickness,” Acta Me-
chanica, Vol. 187, No. 1-4, 2006, pp. 85-102.
[15] W. H. Duan and C. G. Koh, “Axisymmetric Transverse
Vibrations of Circular Cylindrical Shells with Variable
Thickness,” Journal of Sound and Vibration, Vol. 317,
No. 3-5, 2008, pp. 1035-1041.
[16] G. J. Nie and R. C. Batra , “Static Deformations of Func-
tionally Graded Polar-orthotropic Cylinders with Elliptic-
al Inner and Circular Outer Surfaces,” Composites
Science and Technology, Vol. 70, No. 3, 2010, pp.
450-457.
[17] M. Abramowitz and A. I. Stegun, “Handbook of Mathe-
matical Functions,” 5th Edition, US Government Printing
Office, Washington DC, 1966.
[18] H. J. Ding, H. M. Wang and W.Q. Chen, “A Solution of a
Non-homogeneous Orthotropic Cylindrical Shell for
Axisymmetric Plane Strain Dynamic Thermoelastic
Problems,” Journal of Sound and Vibration, Vol. 236, No.
4, 2003, pp. 815-829.
[19] L. S. Srinath, “Advanced Mechanics of Solids,”
McGraw-Hill, India, 1983.