Paper Menu >>
Journal Menu >>
 Applied Mathematics, 2010, 1, 446-455 doi:10.4236/am.2010.16059 Published Online December 2010 (http://www.SciRP.org/journal/am) Copyright © 2010 SciRes. AM Heat and Mass Transfer in MHD Visco-Elastic Fluid Flow through a Porous Medium over a Stretching Sheet with Chemical Reaction Saleh M. Alharbi1, Mohamed A. A. Bazid2, Mahmoud S. El Gendy3* 1Department of Mat hemat i cs, Faculty of Science, Umm AL- Qur a U ni versi ty , Makka h, Sa udi Ara bia 2Department of Mathematics, Faculty of Science, Alkhrj University, Wadi Adawasir, Saudi Arabia 3Department of Mathematics, The University College in Makkah, Makkah, Saudi Arabia E-mail: msmelgendy@yahoo.com Received June 14, 2010; revised August 13, 2010; accepted August 16, 2010 Abstract This paper presents the study of convective heat and mass transfer characteristics of an incompressible MHD vis- co-elastic fluid flow immersed in a porous medium over a stretching sheet with chemical reaction and thermal stratification effects. The resultant governing boundary layer equations are highly non-linear and coupled form of partial differential equations, and they have been solved by using fourth order Runge-Kutta integration scheme with Newton Raphson shooting method. Numerical computations are carried out for the non-dimensional physical parameters. Here a numerical has been carried out to study the effect of different physical parameters such as vis- co-elasticity, permeability of the porous medium, magnetic field, Grashof number, Schmidt number, heat source parameter and chemical reaction parameter on the flow, heat and mass transfer characteristics. Keywords: Heat and Mass Transfer, Incompressible MHD, Visco-Elastic, Porous Medium, Chemical Reaction 1. Introduction In recent years, a great deal of interest has been generat- ed in the area of heat and mass transfer of the boundary layer flow over a stretching sheet, in view of its numer- ous and wide-ranging applications in various fields like polymer processing industry in particular in manufactur- ing process of artificial film and artificial fibers and in some applications of dilute polymer solution. Sakiadis [1,2] was the first study of boundary layer problem as- suming velocity of a boundary sheet as constant. This work is followed by the pioneering work of Tsou et al. [3] studied the flow and heat transfer developed by conti- nuously moving surface both analytically and experi- mentally, in which the flow is caused by an elastic sheet moving in its own plane with a velocity varying linearly with the distance from a fixed point studied by Crane [4]. Chakrabarti and Gupta [5] studied the temperature dis- tribution in this MHD boundary layer flow over a stret- ching sheet in the presence of suction. There are several extensions to this problem, which include consideration of more general stretching velocity and the study of heat transfer [6-14]. In view of increasing importance of non-Newtonian flows, a great deal of work has been carried out to find the similarity solution of viscoelastic fluid flow over im- pervious stretching boundary. Rajagopal et al. [15] ex- amined for a special class of visco-elastic fluids known as second order fluids. Siddappa et al. [16] studied the flow of visoelastic fluids of the type Walter’s liquid B past a stretching sheet. Abel and Veena [17] studied the viscoelasticity on the flow and heat transfer in a porous medium over a stretching sheet. All these studies deals with the studies concerning non-Newtonian flows and heat transfer in the absence of magnetic fields, but pre- sent years we find several industrial applications such as polymer technology and metallurgy [18], where the mag- netic field is applied in the visco-elastic fluid flow. Sar- pakaya [19] was mostly first researcher to investigate MHD flows of non-Newtonian fluids, Andersson [20] investigated the flow problem of electrically conducting viscoelastic fluid past a flat and impermeable elastic *Current Address: Department of Mathematics, The University College in Makkah, Makkah, Saudi Arabia.  S. M. ALHARBI ET AL. Copyright © 2010 SciRes. AM 447 sheet and later his work is extended by many authors [21-25]. Chemical reactions usually accompany a large amount of exothermic and endothermic reactions. These charac- teristics can be easily seen in a lot of industrial processes. Recently, it has been realized that it is not always per- missible to neglect the convection effects in porous con- structed chemical reactors [26]. The reaction produced in a porous medium was extraordinarily in common, such as the topic of PEM fuel cells modules and the polluted underground water because of discharging the toxic sub- stance, etc. Fourier’s law, for instance, described the relation be- tween energy flux and temperature gradient. In other aspects, Fick’s law was determined by the correlation of mass flux and concentration gradient. Moreover, it was found that energy flux can also be generated by compo- sition gradients, pressure gradients, or body forces. The energy flux caused by a composition gradient was dis- covered in 1873 by Dufour and was correspondingly referred to the Dufour effect. It was also called the diffu- sion-thermo effect. On the other hand, mass flux can also be created by a temperature gradient, as was established by Soret. This is the thermal-diffusion effect. In general, the thermal-diffusion and the diffusion-thermo effects were of a smaller order of magnitude than the effects described by Fourier’s or Fick’s law and were often neg- lected in heat and mass transfer processes. There were still some exceptional conditions. The thermal-diffusion effect has been utilized for isotope separation and in mixtures between gases with very light molecular weight (H2, He) and of medium molecular weight (N2, air), the diffusion-thermo effect was found to be of a magnitude such that it may not be neglected in certain conditions [27]. In recent years, Kandasamy et al. studied the heat and mass transfer under a chemical reaction with a heat source [28,29]. Seddeek studied the thermal radiation and buoyancy effect on MHD free convection heat gen- eration flow over an accelerating permeable surface with the influence temperature dependent viscosity [30], and later the chemical reaction, variable viscosity, radiation, variable suction on hydromagnetic convection flow problems were included [31-33]. Although there are numerous widely practical applica- tions in industrial processes, few previous published pa- pers discussed the combined relation. In the present pa- per, we make an attempt to investigate the problem of convective heat and mass transfer of incompressible MHD visco-elastic fluid embedded in a porous medium over a stretching sheet under a chemical reaction. The presence of combined buoyancy effects leads to the mo- mentum, heat and mass transfer equations in the coupled form of highly non-linear partial differential equations. To deal with the coupling and non-linearity, a numerical shooting technique for three unknown initial conditions with Runge-Kutta fourth order integration scheme has been developed. The results are analyzed for various physical parameters such as visco-elasticity, permeability of the porous medium, magnetic field, Grashof number, Schmidt number, Prandtl number, heat source parameter and chemical reaction parameter on the flow, heat and mass transfer characteristics. 2. Mathematical Formulation We consider a free convective, laminar boundary layer flow and heat and mass transfer of viscous incompressi- ble and electrically conducting visco-elastic liquid due to a stretching sheet. The sheet lies in the plane 0y with the flow being confined to 0y. The coordinate x is being taken along the stretching sheet and y is normal to the surfaced, two equal and opposite forces are applied along the x-axis, so that the sheet is stretched, keeping the origin fixed. A uniform transverse magnetic field of strength 0 B is applied parallel to the y-axis and the chemical reaction is taking place in the flow. The viscous dissipation effect and Joule heat are neglected on account of the fluid is finitely conducting. It is assumed that the induced magnetic field, the external electric field and the electric field due to the polarization of charges are negligible. The density variation and the effects of the buoyancy are taken into account in the momentum equa- tion (Boussinesq’s approximation) and the concen- tration of species far from the wall is infinitesimally small and the viscous dissipation term in the energy equ- ation is neglected (as the fluid velocity is very low). Un- der these assumptions, the governing boundary layer equations of momentum, energy and diffusion under Boussinesq approximations could be written as follows: 0 u xy (1) 23322 0 2232 2 *0 uu uuuuuuu uku x yxyxy yxyyy B ug TTgCCu (2) 2 2 pp TTkTQ uTT xyC C y (3) 2 1 2 CC C uDKCC xy y (4) where u, υ are velocity components, T and C are, respectively, the temperature and concentration of che- mical species in the fluid, is the kinematic viscosity, 0 kis the non-Newtonian visco-elastic parameter, εis  S. M. ALHARBI ET AL. Copyright © 2010 SciRes. AM 448 the permeability coefficient of porous medium, g is the acceleration due to gravity, is the volumetric coeffi- cient of thermal expansion, * is the volumetric con- centration coefficient, 0 B is the magnetic induction, is the fluid density, is the fluid electrical conduc- tivity, k is the thermal conductivity, p C is the specific heat at constant pressure, Qis the dimensional heat generation/absorption coefficient, D is the mass diffu- sivity and 1 K is the chemical reaction parameter. The boundary conditions governing the flow are: 0,,0,Α, ,,, , ww y x x yubx CCTTB ll yuu TTCC (5) To take into account the effect of stretching of the boundary sheet, and the effects due to temperature and concentration gradients, we prescribe the wall boundary conditions in the form of (5). In order to study the heat transfer analysis we consider two general cases of non- isothermal temperature boundary conditions, namely boundary with prescribed power law surface temperature. The subscript y denotes the differentiation w.r.t. y. Now, we introduce the following dimensionless va- riables: ',, , ww b ubxf bvfy v TT CC TT CC (6) where , ww x x TT BCCA ll (7) With these changes of variables Equation (1) is iden- tically satisfied and Equations (2)-(4) are transformed to 2'''''' '''''''2' 12 '2'' ' f fffkfffffk f GrGc Mf (8) ''' '0Pr ff (9) ''' '0Sc ff (10) The corresponding boundary conditions take the form: ' ' 0,0,1,1, 1 ,'0,' 0,0,0 ff ff (11) where subscript ' denotes the differentiation with respect to . 12 ,kk are the viscoelastic and porosity parame- ters, Gr and Gc are the free convection parameters, M magnetic field parameter, is the heat generation or absorption coefficient, is the Chemical reaction parameter, and P r, Sc denote Prandtl number and Schmidt number respectively. These dimensionless phy- sical parameters are defined as: * 0 12 22 2 0 1 ,, ,, Pr,,, ww p p gTTgC C kb v kk GrGc vb bx bx CB K Q ScandM kDbCbb (12) where expressions for w TT and w CC are given in Equation (6). The important physical quanti- ties of our interest are the local skin friction w , Nusselt number Nuand Sherwood number Sh and they are defined in the sequel: * '' * 0 0 w y u fwhere y b bx v '0 y w h Nu T tT '(0) y w h Sh C CC 3. Numerical Solution Equations (8)-(10) constitute a highly non-linear coupled boundary value problem of fourth and second order. So we develop most effective numerical shooting technique with fourth-order Runge-Kutta integration scheme with Newton Raphson method. To select we begin with some initial guess value and solve the problem with some particular set of parameters to obtain ''(0),f '(0) and '0 . The solution process is repeated with another larger value of until two successive values of ''(0),f '(0) and '0 differ only after desired digit signifying the limit of the boundary along . The last value of is chosen as appropriate value for that particular set of parameters. Equations (8)-(10) of fourth order in f and second order in and has been reduced to a system of eight simultaneous equations of first order for eight un- knowns following the method of superposition [34]. To solve this system we require eight initial conditions whilst we have only two initial conditions '(0)f and (0) f on f , two initial conditions on each on and . The third initial condition on '''(0)f has been de- duced by applying initial conditions of (11) in Equation (8). Still there are three initial conditions ''(0)f, '(0) and '(0) which are not prescribed. Now, we employ numerical shooting technique where these two ending boundary conditions are utilized to produce two known initial conditions at 0 . In this calculation, the step size Δ0.001 is used while obtaining the numerical 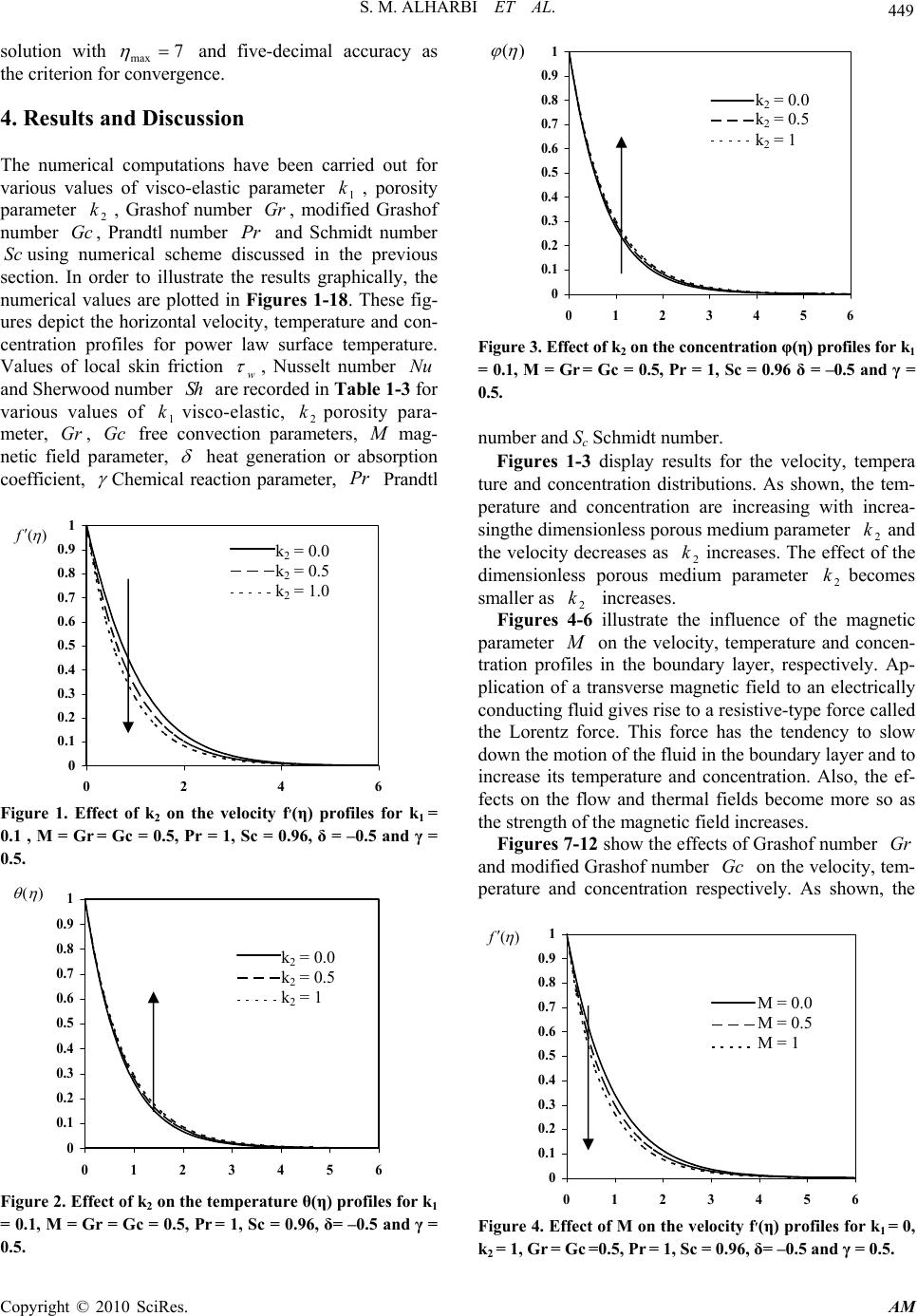 S. M. ALHARBI ET AL. Copyright © 2010 SciRes. AM 449 solution with max 7 and five-decimal accuracy as the criterion for convergence. 4. Results and Discussion The numerical computations have been carried out for various values of visco-elastic parameter 1 k, porosity parameter 2 k, Grashof number Gr , modified Grashof number Gc , Prandtl number P r and Schmidt number Sc using numerical scheme discussed in the previous section. In order to illustrate the results graphically, the numerical values are plotted in Figures 1-18. These fig- ures depict the horizontal velocity, temperature and con- centration profiles for power law surface temperature. Values of local skin friction w , Nusselt number Nu and Sherwood number Sh are recorded in Table 1-3 for various values of 1 kvisco-elastic, 2 kporosity para- meter, Gr, Gc free convection parameters, M mag- netic field parameter, heat generation or absorption coefficient, Chemical reaction parameter, P r Prandtl 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0246 k2= 0. 0 k2= 0. 5 k2= 1. 0 Figure 1. Effect of k2 on the velocity f׳(η) profiles for k1 = 0.1 , M = Gr = Gc = 0.5, Pr = 1, Sc = 0.96, δ = –0.5 and γ = 0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 k2 =0. 0 k2 =0. 5 k2 =1 Figure 2. Effect of k2 on the temperature θ(η) profiles for k1 = 0.1, M = Gr = Gc = 0.5, Pr = 1, Sc = 0.96, δ= –0.5 and γ = 0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 k2=0 .0 k2=0 .5 k2=1 Figure 3. Effect of k2 on the concentration φ(η) profiles for k1 = 0.1, M = Gr = Gc = 0.5, Pr = 1, Sc = 0.96 δ = –0.5 and γ = 0.5. number and Sc Schmidt number. Figures 1-3 display results for the velocity, tempera ture and concentration distributions. As shown, the tem- perature and concentration are increasing with increa- singthe dimensionless porous medium parameter 2 kand the velocity decreases as 2 kincreases. The effect of the dimensionless porous medium parameter 2 kbecomes smaller as 2 k increases. Figures 4-6 illustrate the influence of the magnetic parameter M on the velocity, temperature and concen- tration profiles in the boundary layer, respectively. Ap- plication of a transverse magnetic field to an electrically conducting fluid gives rise to a resistive-type force called the Lorentz force. This force has the tendency to slow down the motion of the fluid in the boundary layer and to increase its temperature and concentration. Also, the ef- fects on the flow and thermal fields become more so as the strength of the magnetic field increases. Figures 7-12 show the effects of Grashof number Gr and modified Grashof number Gc on the velocity, tem- perature and concentration respectively. As shown, the 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 M=0.0 M=0.5 M=1 Figure 4. Effect of M on the velocity f׳(η) profiles for k1 = 0, k2 = 1, Gr = Gc =0.5, Pr = 1, Sc = 0.96, δ= –0.5 and γ = 0.5. ()f k2 = 0.0 k2 = 0.5 k2 = 1.0 () k2 = 0.0 k2 = 0.5 k2 = 1 ()f M = 0.0 M = 0.5 M = 1 )( k2 = 0.0 k2 = 0.5 k2 = 1 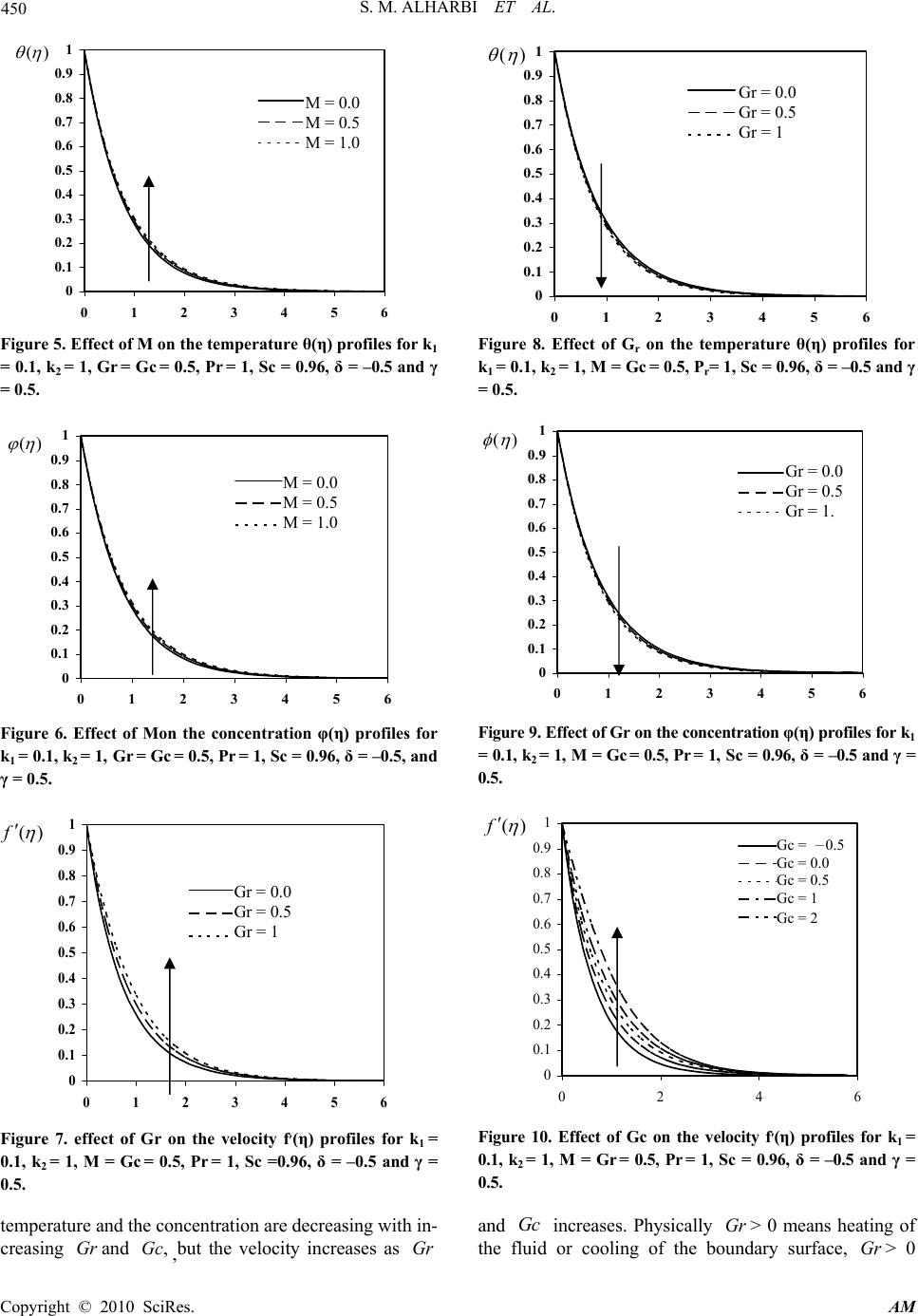 S. M. ALHARBI ET AL. Copyright © 2010 SciRes. AM 450 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 M=0.0 M=0.5 M=1.0 Figure 5. Effect of M on the temperature θ(η) profiles for k1 = 0.1, k2 = 1, Gr = Gc = 0.5, Pr = 1, Sc = 0.96, δ = –0.5 and γ = 0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 M=0.0 M=0.5 M=1.0 Figure 6. Effect of Mon the concentration φ(η) profiles for k1 = 0.1, k2 = 1, Gr = Gc = 0.5, Pr = 1, Sc = 0.96, δ = –0.5, and γ = 0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 Gr=0 . 0 Gr=0 . 5 Gr=1 Figure 7. effect of Gr on the velocity f׳(η) profiles for k1 = 0.1, k2 = 1, M = Gc = 0.5, Pr = 1, Sc =0.96, δ = –0.5 and γ = 0.5. temperature and the concentration are decreasing with in- creasing Gr and ,Gc,but the velocity increases as Gr 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 Gr=0.0 Gr=0.5 Gr=1 Figure 8. Effect of Gr on the temperature θ(η) profiles for k1 = 0.1, k2 = 1, M = Gc = 0.5, Pr= 1, Sc = 0.96, δ = –0.5 and γ = 0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 Gr=0.0 Gr=0.5 Gr=1 Figure 9. Effect of Gr on the concentration φ(η) profiles for k1 = 0.1, k2 = 1, M = Gc = 0.5, Pr = 1, Sc = 0.96, δ = –0.5 and γ = 0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0246 Gc=-0 . 5 Gc=0.0 Gc=0.5 Gc=1 Gc=2 Figure 10. Effect of Gc on the velocity f׳(η) profiles for k1 = 0.1, k2 = 1, M = Gr = 0.5, Pr = 1, Sc = 0.96, δ = –0.5 and γ = 0.5. and Gc increases. Physically Gr> 0 means heating of the fluid or cooling of the boundary surface, Gr> 0 )( )( ()f () () ()f M = 0.0 M = 0.5 M = 1.0 M = 0.0 M = 0.5 M = 1.0 Gr = 0.0 Gr = 0.5 Gr = 1 Gc = -0.5 Gc = 0.0 Gc = 0.5 Gc = 1 Gc = 2 Gr = 0.0 Gr = 0.5 Gr = 1. Gr = 0.0 Gr = 0.5 Gr = 1  S. M. ALHARBI ET AL. Copyright © 2010 SciRes. AM 451 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0246 Gc=-0.5 Gc=0.5 Gc=2 Figure 11. effect of Gc on the temperature θ(η) profiles fvor k1 = 0.1, k2 = 1, M = Gr = 0.5, Pr = 1, Sc = 0.96, δ = –0.5 and γ = 0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0246 Gc=-0.5 Gc=0.5 Gc=2 Figure 12. Effect of Gc on the concentration φ(η) profiles for k1 = 0.1, k2 =1, M = Gr = 0.5, Pr = 1, Sc = 0.96, δ = –0.5 and γ = 0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456789 δ=1 δ=-0.5 δ=0.0 δ=0.3 Figure 13. Effect of δ on the velocity f׳(η) profiles for k1 = 0.1, k2 = 1, M = Gr = Gc = 0.5, Pr = 1, Sc = 0.96 and γ = 0.5. means cooling of the fluid or heating of the boundary sur- face and Gr= 0 corresponds to the absence of free con- 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0246810 δ=-1 δ=-0.5 δ=0.0 δ=0.3 Figure 14. Effect of δ on the temperature θ(η) profiles for k1 = 0.1, k2 = 1, M = Gr = Gc = 0.5, Pr = 1, Sc = 0.96 and γ = 0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 δ=-1 δ=-0.5 δ=0.0 δ=0.3 Figure 15. Effect of δ on the concentration φ(η) profiles for k1 = 0.1, k2 = 1, M = Gr = Gc = 0.5, Pr = 1, Sc = 0.96 and γ = 0.5. vection current. Figures 13-15 present typical profiles for the velocity, temperature and concentration for various values of a heat source (0 ) or a heat sink (0 ), respectively. As shown, the velocity and the temperature are increas- ing with increasing , but the concentration decreases as increases. In the event that the strength of the heat sink (0 ) is relatively large, the maximum fluid tem- perature does not occur at the wall but rather in the fluid region close to it. Conversely, the presence of a heat source (0 ) effect causes a reduction in the thermal state of the fluid, thus producing lower thermal boundary layers. Figures 16-18 illustrate the influence of the Chemical reaction parameter on the velocity, temperature and concentration profiles in the boundary layer, respectively. As shown, the velocity and the concentration are decr- easing with increasing , but the temperature increases Gc = -0.5 Gc = 0.5 Gc = 2 Gc = -0.5 Gc = 0.5 Gc = 2 δ = -1 δ = -0.5 δ = 0.0 δ = 0.3 δ = -1 δ = -0.5 δ = 0.0 δ = 0.3 δ = 1 δ = -0.5 δ = 0.0 δ = 0.3  S. M. ALHARBI ET AL. Copyright © 2010 SciRes. AM 452 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 02468 γ=-0.2 γ=0.0 γ=0.5 γ=1 Figure 16. Effect of γ on the velocity f׳(η) profiles for k1 = 0.1, k2 = 1, M = Gr = Gc = 0.5, Pr = 1, Sc = 0.96 and δ = –0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0123456 γ=-0.2 γ=0.0 γ=0.5 γ==1 Figure 17. Effect of γ on the temperature θ(η) profiles for k1 = 0.1,k2 = 1, M = Gr = Gc = 0.5, Pr = 1, Sc = 0.96 and δ = –0.5. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0246810 γ=-0.2 γ=0.0 γ=0.5 γ=1 Figure 18. Effect of γ on the concentration φ(η) profiles for k1 = 0.1, k2 = 1, M = Gr = Gc = 0.5, Pr = 1,Sc = 0.96 and δ = –0.5. as increases, this is due to the fact that destructive chemical reduces the solutal boundary layer thickness and increases the mass transfer. Tables 1-3 represents values of w , Nu and Sh for various values of 1 ,,,,,Pr, , M Gr GcSck and 2 k. It is clear that, with increasing Gr and Gc, ,Nu Sh and w increases, whereas with increasing 1,k 2 kand M , ,Nu Shand w decreases. Also, w and Sh increase as Sc and increases and Nu decrease, whereas, Nu and w decreases and Sh increase as increases, Also, Sh and w increases and Nu decrease as P rin- crease. Table 1. The effect of parameter on(0).f (0)f k 1 = 0.3 k 1 =0.2 k 1 = 0.1 k 2M G r Gc P r δ Sc γ – 0.9233 – 0.8908 – 0.86260.00.50.50.51.0 – 0.5 0.96 0.5 – 1.1978 – 1.1344 – 1.08380.50.50.50.51.0 – 0.5 0.96 0.5 – 1.4345 – 1.3476 – 1.27911.00.50.50.51.0 – 0.5 0.96 0.5 – 1.1978 – 1.1344 – 1.08381.00.00.50.51.0 – 0.5 0.96 0.5 – 1.4345 – 1.3476 – 1.27911.00.50.50.51.0 – 0.5 0.96 0.5 – 1.6446 – 1.5387 – 1.45521.01.00.50.51.0 – 0.5 0.96 0.5 – 1.6639 – 1.556 – 1.46921.00.50.00.51.0 – 0.5 0.96 0.5 – 1.4345 – 1.3476 – 1.27911.00.50.50.51.0 – 0.5 0.96 0.5 – 1.1994 – 1.1400 – 1.09291.00.51.00.51.0 – 0.5 0.96 0.5 – 1.8913 – 1.7696 – 1.66881.00.5 0.5 – 0.5 1.0 – 0.5 0.96 0.5 – 1.6654 – 1.5578 – 1.47121.00.50.50.01.0 – 0.5 0.96 0.5 – 1.4345 – 1.3476 – 1.27911.00.50.50.51.0 – 0.5 0.96 0.5 – 1.4345 – 1.3476 – 1.27911.00.50.50.51.0 – 0.5 0.96 0.5 – 1.4622 – 1.379 – 1.31201.00.50.50.52.0 – 0.5 0.96 0.5 – 1.5010 – 1.4201 – 1.35311.00.50.50.55.5 – 0.5 0.96 0.5 – 1.4457 – 1.3602 – 1.29221.00.50.50.51.0 – 1.0 0.96 0.5 – 1.4345 – 1.3476 – 1.27911.00.50.50.51.0 – 0.5 0.96 0.5 – 1.4165 – 1.3268 – 1.25711.00.50.50.51.00.0 0.96 0.5 – 1.4034 – 1.3110 – 1.24021.00.50.50.51.00.2 0.96 0.5 – 1.4345 – 1.3476 – 1.27911.00.50.50.51.0 – 0.5 0.96 0.5 – 1.4637 – 1.3808 – 1.31401.00.50.50.51.0 – 0.5 2.0 0.5 – 1.5025 – 1.4219 – 1.35511.00.50.50.51.0 – 0.5 5.0 0.5 – 1.4032 – 1.3106 – 1.23971.00.50.50.51.0 – 0.5 0.96 – 0.2 – 1.4164 – 1.3267 – 1.25691.00.50.50.51.0 – 0.5 0.96 0.0 – 1.4345 – 1.3476 – 1.27911.00.50.50.51.0 – 0.5 0.96 0.5 – 1.4457 – 1.3603 – 1.29231.00.50.50.51.0 – 0.5 0.96 1.0 γ = -0.2 γ = 0.0 γ = 0.5 γ = 1 γ = -0.2 γ = 0.0 γ = 0.5 γ = 1 γ = -0.2 γ = 0.0 γ = 0.5 γ = 1 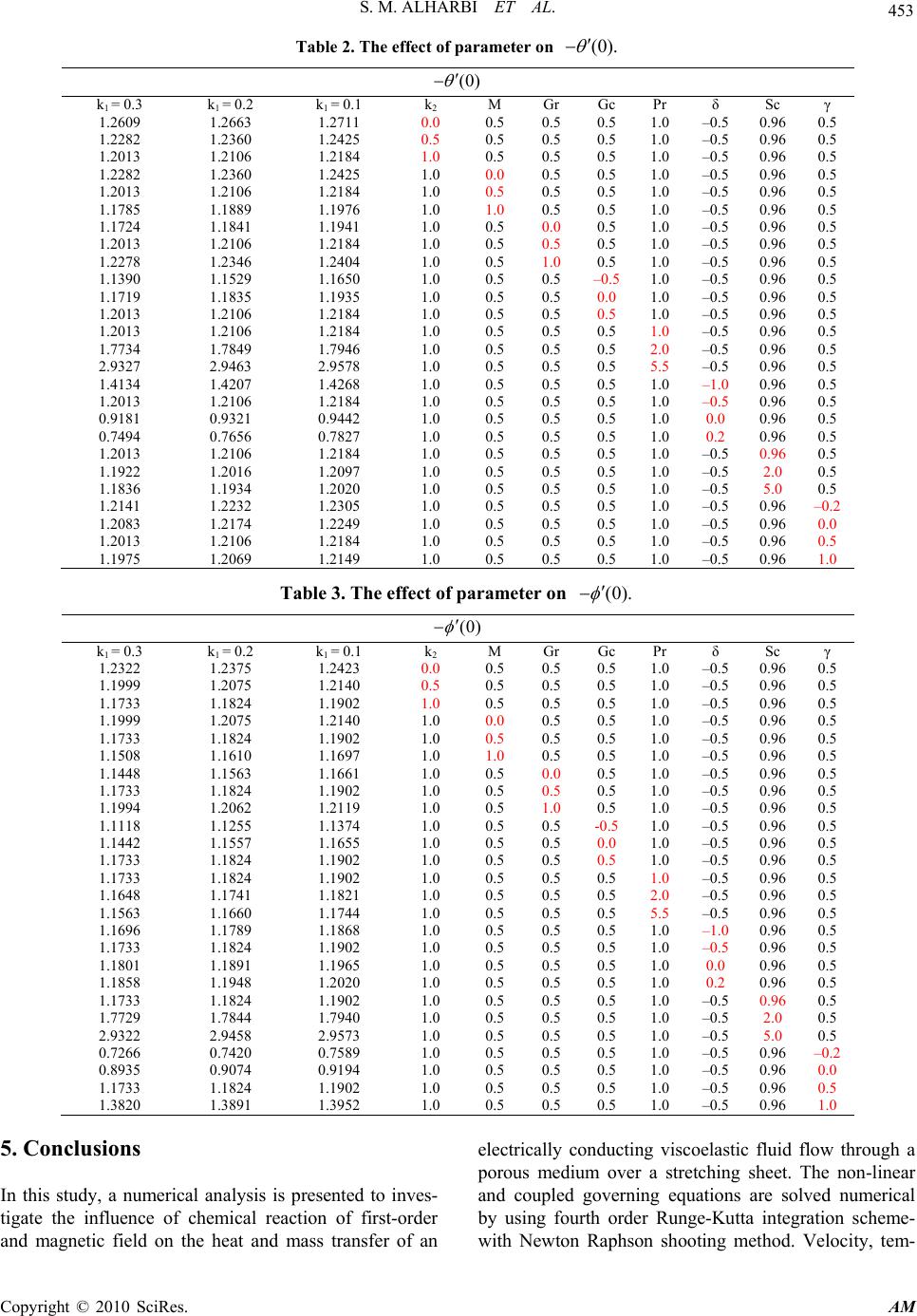 S. M. ALHARBI ET AL. Copyright © 2010 SciRes. AM 453 Table 2. The effect of parameter on (0). (0) k1 = 0.3 k1 = 0.2 k1 = 0.1k2MGr Gc Pr δ Sc γ 1.2609 1.2663 1.2711 0.00.50.50.51.0 –0.5 0.96 0.5 1.2282 1.2360 1.2425 0.5 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.2013 1.2106 1.2184 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.2282 1.2360 1.2425 1.00.00.50.51.0 –0.5 0.96 0.5 1.2013 1.2106 1.2184 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.1785 1.1889 1.1976 1.0 1.0 0.5 0.5 1.0 –0.5 0.96 0.5 1.1724 1.1841 1.1941 1.00.50.00.51.0 –0.5 0.96 0.5 1.2013 1.2106 1.2184 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.2278 1.2346 1.2404 1.0 0.5 1.0 0.5 1.0 –0.5 0.96 0.5 1.1390 1.1529 1.1650 1.00.50.5–0.5 1.0–0.5 0.96 0.5 1.1719 1.1835 1.1935 1.0 0.5 0.5 0.0 1.0 –0.5 0.96 0.5 1.2013 1.2106 1.2184 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.2013 1.2106 1.2184 1.00.50.50.51.0 –0.5 0.96 0.5 1.7734 1.7849 1.7946 1.0 0.5 0.5 0.5 2.0 –0.5 0.96 0.5 2.9327 2.9463 2.9578 1.0 0.5 0.5 0.5 5.5 –0.5 0.96 0.5 1.4134 1.4207 1.4268 1.00.50.50.51.0 –1.0 0.96 0.5 1.2013 1.2106 1.2184 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 0.9181 0.9321 0.9442 1.0 0.5 0.5 0.5 1.00.0 0.96 0.5 0.7494 0.7656 0.7827 1.0 0.5 0.5 0.5 1.0 0.2 0.96 0.5 1.2013 1.2106 1.2184 1.00.50.50.51.0 –0.5 0.96 0.5 1.1922 1.2016 1.2097 1.0 0.5 0.5 0.5 1.0 –0.5 2.0 0.5 1.1836 1.1934 1.2020 1.0 0.5 0.5 0.5 1.0–0.5 5.0 0.5 1.2141 1.2232 1.2305 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 –0.2 1.2083 1.2174 1.2249 1.00.50.50.51.0 –0.5 0.96 0.0 1.2013 1.2106 1.2184 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.1975 1.2069 1.2149 1.0 0.5 0.5 0.5 1.0–0.5 0.96 1.0 Table 3. The effect of parameter on (0). (0) k1 = 0.3 k1 = 0.2 k1 = 0.1k2MGr Gc Pr δ Sc γ 1.2322 1.2375 1.2423 0.00.50.50.51.0 –0.5 0.96 0.5 1.1999 1.2075 1.2140 0.5 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.1733 1.1824 1.1902 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.1999 1.2075 1.2140 1.00.00.50.51.0 –0.5 0.96 0.5 1.1733 1.1824 1.1902 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.1508 1.1610 1.1697 1.0 1.0 0.5 0.5 1.0 –0.5 0.96 0.5 1.1448 1.1563 1.1661 1.00.50.00.51.0 –0.5 0.96 0.5 1.1733 1.1824 1.1902 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.1994 1.2062 1.2119 1.0 0.5 1.0 0.5 1.0 –0.5 0.96 0.5 1.1118 1.1255 1.1374 1.00.50.5 -0.51.0 –0.5 0.96 0.5 1.1442 1.1557 1.1655 1.0 0.5 0.5 0.0 1.0 –0.5 0.96 0.5 1.1733 1.1824 1.1902 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.1733 1.1824 1.1902 1.00.50.50.51.0 –0.5 0.96 0.5 1.1648 1.1741 1.1821 1.0 0.5 0.5 0.5 2.0 –0.5 0.96 0.5 1.1563 1.1660 1.1744 1.0 0.5 0.5 0.5 5.5 –0.5 0.96 0.5 1.1696 1.1789 1.1868 1.00.50.50.51.0 –1.0 0.96 0.5 1.1733 1.1824 1.1902 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.1801 1.1891 1.1965 1.0 0.5 0.5 0.5 1.00.0 0.96 0.5 1.1858 1.1948 1.2020 1.0 0.5 0.5 0.5 1.0 0.2 0.96 0.5 1.1733 1.1824 1.1902 1.00.50.50.51.0 –0.5 0.96 0.5 1.7729 1.7844 1.7940 1.0 0.5 0.5 0.5 1.0 –0.5 2.0 0.5 2.9322 2.9458 2.9573 1.0 0.5 0.5 0.5 1.0–0.5 5.0 0.5 0.7266 0.7420 0.7589 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 –0.2 0.8935 0.9074 0.9194 1.00.50.50.51.0 –0.5 0.96 0.0 1.1733 1.1824 1.1902 1.0 0.5 0.5 0.5 1.0 –0.5 0.96 0.5 1.3820 1.3891 1.3952 1.0 0.5 0.5 0.5 1.0–0.5 0.96 1.0 5. Conclusions In this study, a numerical analysis is presented to inves- tigate the influence of chemical reaction of first-order and magnetic field on the heat and mass transfer of an electrically conducting viscoelastic fluid flow through a porous medium over a stretching sheet. The non-linear and coupled governing equations are solved numerical by using fourth order Runge-Kutta integration scheme- with Newton Raphson shooting method. Velocity, tem-  S. M. ALHARBI ET AL. Copyright © 2010 SciRes. AM 454 perature and concentration profiles are presented graphi- cally and analyzed. The fundamental parameters found to effect the problem under consideration are the chemical reaction parameter, magnetic field parameter, viscoelas- tic parameter, porosity parameter, Grashof number, mo- dified Grashof number, Prandtl number, Schmidt number and heat absorption parameter. It is found that, the tem- perature as well as concentration increases with increas- ing the visco-elastic parameter, porosity parameter and magnetic parameter whereas reverse trend is seen with Grashof number and modified Grashof number increas- ing. Additionally, the velocity temperature is increased in the presence of heat absorption parameters and decreased with chemical reaction. 6. References [1] B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surfaces: I. Boundary Layer Equations for Two Dimensional and Axisymmetric Flow,” AICHE Journal, Vol. 7, No. 1, March 1961, pp. 26-28. [2] B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surfaces: II. Boundary Layer on a Continuous Flat Surface,” AICHE Journal, Vol. 7, 1961, pp. 221-225. [3] F. K. Tsou, E. M. Sparrow and R. J. Goldstein, “Flow and Heat Transfer in the Boundary Layer on a Continuous Moving Surface,” International Journal of Heat and Mass Transfer, Vol. 10, 1967, pp. 219-223. [4] L. J. Crane, “Flow past a Stretching Plate,” Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 21, No. 4, 1970, pp. 645-647. [5] A. Chakrabarti and A. S. Gupta, “Hydromagnetic flow and heat transfer over a stretching sheet,” Quarterly Journal of Mechanics and Applied Mathematics, Vol. 37, 1979, pp. 73-78. [6] C. K. Chen and M. I. Char, “Heat Transfer of a Conti- nuous Stretching Surface with Suction or Blowing,” Journal of Mathematical Analysis and Applications, Vol. 135, No. 2, November 1988, pp. 568-580. [7] T. C. Chiam, “Heat Transfer in a Variable Conductivity in a Stagnation Point Flow towards a Stretching Sheet,” International Communications in Heat and Mass Trans- fer, Vol. 23, No. 2, March-April 1996, pp. 239-248. [8] E. M. Abo Eldahab and M. S.El Gendy, “Radiation Effect on Convective Heat Transfer in an Electrically Conducting Fluid at a Stretching surface with Variable Viscosity and Uniform Free-Stream,” Physica Scripta, Vol. 62, No. 4, 2000, pp. 321-325. [9] E. M. Abo Eldahab and M. S. El Gendy, “Convective Heat Transfer past a Continuously Moving Plate Embed- ded in a Non-Darcian Porous Medium in the Presence of a Magnetic Field,” Canadian Journal of Physics, Vol. 79, 2001, pp. 1031-1038. [10] A. A. Megahed, S. R. Komy and A. A. Afify, “Similarity Analysis in Magnetohydrodynamics Hall Effect on Free Convection Flow and Mass Transfer past Semi Infinite Vertical Flat Plate,” International Journal of Non-Linear Mechanics, Vol. 38, 2003, pp. 513-520. [11] M. A. Seddeek, “Effects of Non-Darcian on Forced Con- vection Heat Transfer over a Flat Plate in a Porous Me- dium-with Temperature Dependent Viscosity,” Interna- tional Communications in Heat and Mass Transfer, Vol. 32, 2005, pp. 258-265. [12] M. A. Seddeek and M. S. Abdelmeguid, “Effects of Rad- iation and Thermal Diffusivity on Heat Transfer over a Stretching Surface with Variable Heat Flux,” Physics Letters A, Vol. 348, No. 3-6, January 2006, pp. 172-179. [13] A. A. Afify, “Similarity Solution in MHD: Effects of Thermal Diffusion and Diffusion Thermo on Free Con- vective Heat and Mass Transfer over a Stretching Surface Considering Suction or Injection,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 5, May 2009, pp. 2202-2214 [14] M. A. Seddeek, S. N. Odda and M. S. Abdelmeguid, “Numerical Study for the Effects of Thermophoresis and Variable Thermal Conductivity on Heat and Mass Trans- fer over an Accelerating Surface with Heat Source,” Computational Materials Science, Vol. 47, No. 1, 2009, pp. 93-98. [15] K. R. Rajagopal, T. Y. Na and A. S. Gupta, “Flow of Visco-Elastic Fluid over a Stretching Sheet,” Rheol Acta, Vol. 23, 1984, pp. 213-215. [16] B. Siddappa and S. Abel, “Non-Newtonian flow past a stretching plate,” Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 36, 1985, pp. 890-892. [17] S. Abel and P. H. Veena, “Visco-Elastic Fluid Flow and Heat Transfer in Porous Medium over a Stretching Sheet,” International Journal of Non-Linear Mechanics, Vol. 33, 1998, pp. 531-540. [18] A. Chakrabarti and A. S. Gupta, “Hydromagnetic Flow and Heat Transfer over a Stretching Sheet,” Quarterly Journal of Mechanics and Applied Mathematics, Vol. 37, 1979, pp. 73-78. [19] T. Sarpakaya, “Flow of Non-Newtonian Fluids in Mag- netic Field,” AICHE Journal, Vol. 7, 1961, pp. 324-328. [20] H. I. Andersson, “MHD Flow of Viscoelastic Fluid past a Stretching Surface,” Acta Mechanica, Vol. 95, 1992, pp. 227- 230. [21] S. Abel, A. Joshi and R. M. Sonth, “Heat Transfer in a MHD Visco-Elastic Fluid over a Stretching Surface,” Journal of Applied Mathematics and Mechanics, Vol. 81, 2001, pp. 691-698. [22] S. Abel, P. H. Veena, K. Rajgopal and V. K. Pravin, “Non-Newtonian Magneto Hydrodynamic Flow over a Stretching Surface with Heat and Mass Transfer,” Inter- national Journal of Non-Linear Mechanics, Vol. 39, 2004, pp. 1067-1078. [23] M. A. Seddeek, “Heat and Mass Transfer on a Stretching Sheet with a Magnetic Field in a Visco-Elastic Fluid Flow through a Porous Medium with Heat Source or Sink,” Computational Materials Science, Vol. 38, 2007, pp. 781-787.  S. M. ALHARBI ET AL. Copyright © 2010 SciRes. AM 455 [24] S. Abel and N. Mahesha, “Heat Transfer in MHD Vis- coelastic Fluid Flow over a Stretching Sheet with Varia- ble Thermal Conductivity, Non-Uniform Heat Source and Radiation,” Applied Mathematical Modelling, Vol. 32, 2008, pp. 1965-1983. [25] K. V. Prasad, D. Pal, V. Umesh and N. S. Prasanna Rao, “The Effect of Variable Viscosity on MHD Viscoelastic Fluid Flow and Heat Transfer over a Stretching Sheet,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 2, February 2010, pp. 331-344. [26] D. A. Nield and A. Bejan, “Convection in Porous Me- dia,” 2nd Edition, Springer-Verlag, New York, 1999. [27] E. R. G. Eckert and R. M. Drake, “Analysis of Heat and Mass Transfer,” McGraw-Hill, New York, 1972. [28] R. Kandasamy, K. Periasamy and K. K. Sivagnana Prab- hu, “Chemical Reaction, Heat and Mass Transfer on MHD Flow over a Vertical Stretching Surface with Heat Source and Thermal Stratification Effects,” International Journal of Heat and Mass Transfer, Vol. 48, No. 21-22, October 2005, pp. 4557- 4561. [29] R. Kandasamy, K. Periasamy and K. K. S. Prabhu, “Ef- fect of Chemical Reaction, Heat and Mass Transfer along a Wedge with Heat Source and Concentration in the Presence of Suction or Injection,” International Journal of Heat and Mass Transfer, Vol. 48, No. 7, March 2005, pp. 1388-1394. [30] M. A. Seddeek, “Thermal Radiation and Buoyancy Ef- fects on MHD Free Convection Heat Generation Flow over an Accelerating Permeable Surface with Tempera- ture Dependent Viscosity,” Canadian Journal of Physics, Vol. 79, 2001, pp. 725-732. [31] M. A. Seddeek, A. A. Darwish and M. S. Abdelmeguid, “Effect of Chemical Reaction and Variable Viscosity on Hydromagnetic Mixed Convection Heat and Mass Transfer for Hiemenz Flow through Porous Media with Radiation,” Communications in Nonlinear Science and Numerical Simulation, Vol. 12, No. 2, March 2007, pp. 195-213. [32] M. A. Seddeek and A. M. Salem, “The Effect of an Axial Magnetic Field on The Flow and Heat Transfer about a Fluid Underlying the Axisymmetric Spreading Surface with Temperature Dependent Viscosity and Thermal Dif- fusivity,” Computional Mechanics, Vol. 39, No. 4, 2007, pp. 401-408. [33] M. A. Seddeek, F. A. Salama, “The Effects of Tempera- ture Dependent Viscosity and Thermal Conductivity on Unsteady MHD Convective Heat Transfer Past a Semi-Infinite Vertical Porous Moving Plate with Variable Suction,” Computational Materials Science, Vol. 40, No. 2, August 2007, pp. 186-192. [34] T. Y. Na, “Computational Methods in Engineering Boun- dary Value Problems,” Academic Press, New York, 1979. Nomenclature , A B constants T temperature of the ambient fluid b stretching rate, positive constant w T surface temperature 0 B magnetic induction ,u velocity components along x and y direction p C specific heat at constant pressure x coordinate along the stretching sheet D mass diffusivity ydistance normal to the stretching sheet f dimensionless stream function Greek symbols Gr temperature Grashof of number dimensionless temperature function Gc mass Grashof of number dimensionless concentration function g acceleration due to gravity dimensionless space variable 1 K first order chemical reaction rate kinematic viscosity k thermal conductivity fluid density 0 k non-Newtonian visco-elastic parameter electrical conductivity 1 k visco-elastic parameter coefficient of viscosity 2 k porosity parameter coefficient of thermal expansion l characteristic length * volumetric concentration coefficient M magnetic field parameter heat generation or absorption coefficient Nu Nusselt number w skin friction P r Prandtl number permeability coefficient of porous medium Q dimensional heat generation/absorption coefficient Chemical reaction parameter Sc Schmidt number Subscripts Sh Sherwood number w properties at the plate T temperature of the fluid free stream condition |

