Advances in Materials Physics and Chemistry, 2013, 3, 178-184
http://dx.doi.org/10.4236/ampc.2013.32025 Published Online June 2013 (http://www.scirp.org/journal/ampc)
Ab Initio Study of the Electronic and Vibrational Pr operties
of 1-nm-Diameter Single-Walled Nanotubes
Jesús Marquina1, Chrystian Power2, Jesús González2,3, Jean-Marc Broto4
1Centro de Estudios Avanzado en Óptica, Facultad de Ciencias, Universidad de los Andes, Mérida, Venezuela
2Centro de Estudios de Semiconductores, Facultad de Ciencias, Universidad de los Andes, Mérida, Venezuela
3Malta Consolider Team, CITIMAC, Facultad de Ciencias, Universidad de Cantabria, Santander, España
4LNCMI, Paul Sabatier University, Toulouse, France
Received February 19, 2013; revised April 25, 2013; accepted May 10, 2013
Copyright © 2013 Jesús Marquina et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
The electronic structure, band gap, density of states of the (8,8), (14,0) and (12,3) single-walled carbon nanotubes by
the SIESTA (Spanish Initiative for Electronic Simulations with Thousands of Atoms) method in the framework den-
sity-functional theory (DFT) with the generalized gradients approximation (GGA) were studied. Also, we studied the
vibrational properties of the (8,8) and (14,0) nanotubes. Only the calculated relaxed geometry for (12,3) nanotube show
significant deviations from the ideal rolled graphene sheet configuration. The electronic transition energies of van Hove
singularities were studied and compared with previous results. The calculated band structures, density of states and dis-
persion curves for all tubes were in good agreement with theoretical and experimental results.
Keywords: Carbon Nanotubes; Electronic Structure; Dispersion Curve
1. Introduction
Carbon nanotubes can be regarded as graphitic cylinders
generated just by rolling one sheet of graphene with a
finite width [1]. Also it is known that a nanotube can be
metallic or semiconducting depending on their diameter
and chirality [2-4]. In recent years, it has attracted great
attention in many fields of science and technology be-
cause of its novel and unique structural and electronic
properties [5]. Nanotubes are promising for applications,
such as probes and sensors; tips for atomic force mi-
croscopy, gas sensors, biosensors and physical sensors
[6].
There has been much theorical and experimental work
on the vibrational and electronic properties of carbon
nanotubes. The first theorical calculation of SWCNT’s
electronic structure was carried out using zone folding
scheme [7,8]. Within this framework, all the armchair
nanotubes (n,n) are expected to be metallic, while ap-
proximately one third of zigzag (n,0) and chiral (n,m)
tubes should be metallic, with remainder being semicon-
ducting [3,4]. The zone-folding scheme in general works
reasonably well and has proven immense success in pro-
viding physically relevant information on the nature of
electronic and vibrational interactions in carbon nano-
tubes [9,10]. However, previous studies show the effects
of the σ-π hybridization in small diameter SWCNT’s on
their electronic properties [11,12]. An example of par-
ticular importance is the (5,0) nanotube which has been
demonstrated by ab initio (using local density approxi-
mation in the framework of the density-functional theory)
and symmetry-adapted non-orthogonal tight-binding cal-
culations to be a metal [12-14] but not a semiconductor
with a moderate gap as reported in the previous π-band
tight-binding work [2,3].
The phonon dispersion curves over the full Brillouin
zone are useful in such fields as the inelastic neutron
scattering [15], Second-order Raman spectroscopy [16],
double-resonance processes [17-20] and the electron-
phonon interactions [21-24]. The calculations of the
phonon dispersions have been made using both empirical
methods and the accuracy ab initio calculations. Initial
work on this problem using zone folding and force con-
stant models [9,25-27] shows that the zone-folding me-
thod has two shortcomings: the structural relaxation ef-
fect has been completely ignored which makes the trans-
ferability of the phonon spectra between the graphene
and the SWCNT’s a serious question and that the vibra-
tional eigenvectors are also different from the graphene
to the SWCNT’s. The ab initio phonon dispersion is
C
opyright © 2013 SciRes. AMPC

J. MARQUINA ET AL. 179
advantageous because such calculations do not depend
on any predefined parameter. There are different authors
that have reported ab initio phonon dispersion of
SWCNT’s, all using the supercell approach [11,28,29].
One way to study the structural and mechanical prop-
erties of carbon nanotubes is by applying hydrostatic
pressure. A recent study shows that in DWCNT’s the
outer tube acts as a protection shield for the inner tube (at
least up 11 GPa) [30,31]. This means that the inner tube
retains its properties as single-walled nanotube. In Fig-
ures 5 and 6 of Ref. [30], the Raman spectrums of the
radial breathing modes (RBM) of the inner and the outer
shells of pristine and filled DWCNT’s have been observed,
respectively. In both in pristine or Te-filled DWCNT’s
tubes with diameters around 1 nm for the inner tubes of
DWCNT’s are presented.
In this paper, we present first-principles calculations of
the structural, electronic, and vibrational properties of
SWCNT’s about 1 nm in diameter to address the point
mentioned above. We will discuss the relaxed geometry
of the (8,8), (14,0) and (12,3) nanotubes comparing it to
the ideal cylindrical configuration. We also examine the
importance of the detailed structure in discussing elec-
tronic properties of nanotubes. Finally, we discuss about
phonon dispersion curves for the (8,8) nanotube.
2. Computational Method
Our first-principles calculations are based on density
functional theory (DFT) employ a numerical-atomic-
orbital basis set. We used the package SIESTA ab initio
simulation package [32]. We worked within the gradient
generalized approximation (GGA) as parametrized by
Perdew-Burke-Ernzerhof (PBE) [33]. The core electrons
were replaced by pseudopotentials of the type Troullier-
Martins [34], the valence electrons were described by
localized pseudo-atomic orbitals [35]. The valence elec-
trons were described by a double-ζ polarized basis set
with a cutoff radius of 4.99 a.u. for the s and 6.25 for the
p and the polarizing d orbitals, as is determined from an
energy shift of 50 meV by localization. These values
have been tested by M. Machón et al. [12]. They found
that an increasing of the cutting of the orbitals only pro-
duces changes in the total energies less than 0.1 meV/
atom and none significant effect neither on the structure
nor on the energies of electronic states was observed.
The dynamical matrix was found by a finite-difference
approach, this is, calculating the Hellman-Feynmann
forces for displaced atoms.
Calculations were performed for the following tubes:
(8,8), (14,0) and (12,3). They were all considered as iso-
lated. For that purpose, we used periodic-boundary con-
ditions on supercell geometry with sufficient lateral
separation among neighboring tubes. For the purpose of
sampling the Brillouin zone in the direction of the tube
axis, as well as for the computation of the force-constant
matrix for phonon calculations, we used supercells con-
sisted of five unit cells for the armchair (8,8) tube with
160 atoms and three unit cells for zigzag (14,0) tube with
162 atoms. The supercell length (about 1 nm) in the tube-
axis direction is not too different from one another. We
are aware that the supercell should be large enough so
that the effect of the image displacement is negligible
[11].
3. Results and Discussion
3.1. Dispersion Curve of Graphene
In Figure 1 we show the phonon frequencies of graphene
calculated from first principles. This will serve as a test
of accuracy of the calculation method. In general, a good
agreement between our calculations and experiment (see
Ref. [36]) for the TO, LO and LA branches is found.
This shows the accuracy of the basis set used in this work.
We optimized the bond length of a graphene sheet in a
supercell with the interlayer distance being 10 Å, which
can be considered enough to neglect the interlayer inter-
action. The bond length of graphite obtained by this op-
timization is 1.437 Å, which is 1.5% higher than the ex-
perimental value (1.416 Å) [37]. The small splitting of
the LO and LA phonons at the M point equal to 33 cm−1
coincides with the experimental value reported by inelas-
tic x-ray scattering [36]. While, our calculated splitting
between TO and LA modes at the K point 118 cm−1 is
different from experimental value 71 cm−1. Other theo-
retical values have been reported; Pavone et al. [38] ob-
tained a splitting of 120 cm−1 and a value of 140 cm−1 by
using LDA was also reported [28]. The zone center pho-
non value 1575 cm−1 is slightly below the experimental
values for graphite and grapheme (1582 cm−1) measured
recently [39]. These differences can be explained by tak-
ing into account that other authors have estimated uncer-
tainties of 10 cm−1 for the frequencies higher than 1300
cm−1 [11,40].
Figure 1. Ab initio calculations of the phonon dispersion of
graphene. We used a supercell with 98 atoms. The mesh
cutoff was 350 Ry, with 3321 k points and a 50 meV PAO
energy shift.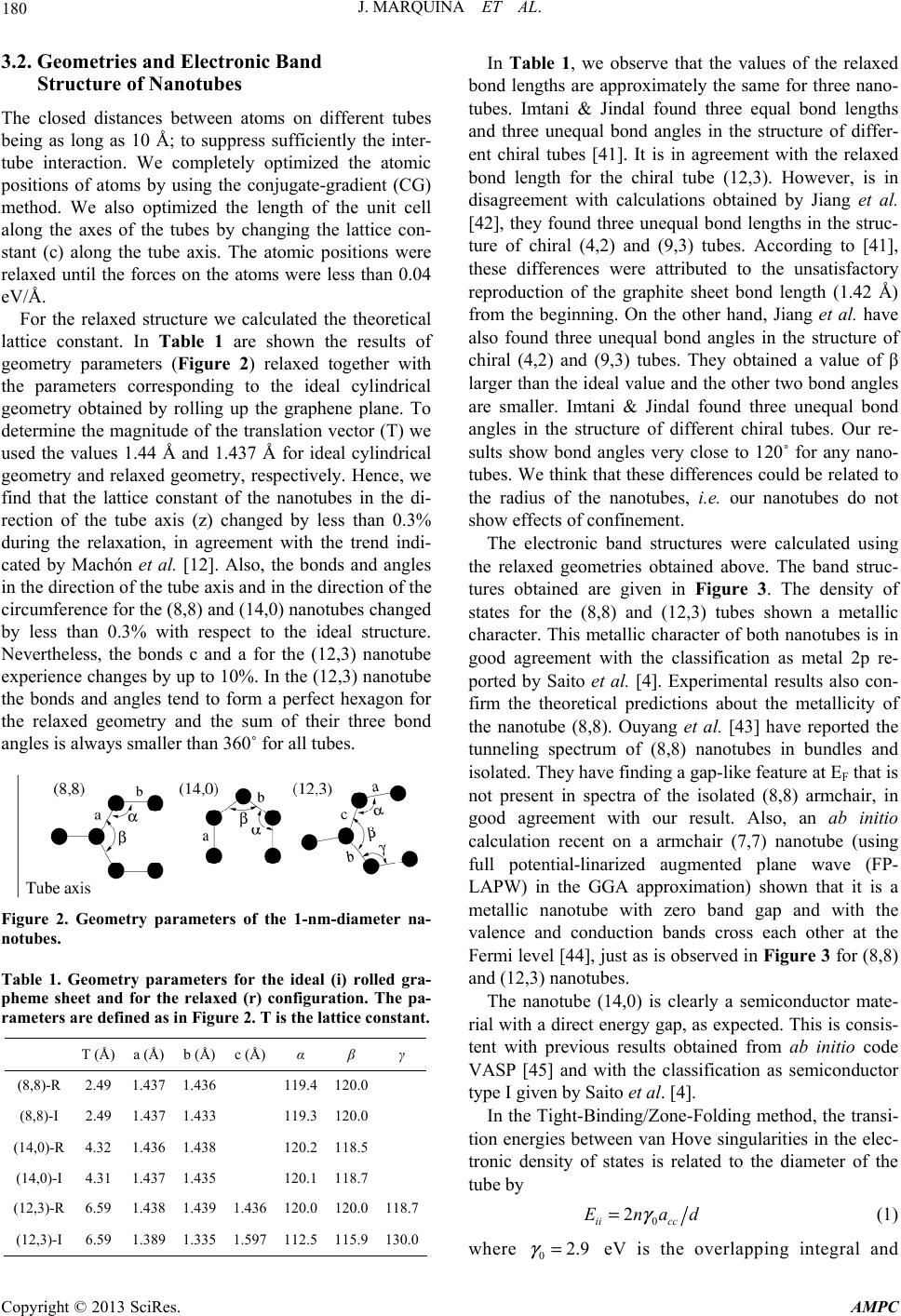

J. MARQUINA ET AL.
180
3.2. Geometries and Electronic Band
Structure of Nanotubes
The closed distances between atoms on different tubes
being as long as 10 Å; to suppress sufficiently the inter-
tube interaction. We completely optimized the atomic
positions of atoms by using the conjugate-gradient (CG)
method. We also optimized the length of the unit cell
along the axes of the tubes by changing the lattice con-
stant (c) along the tube axis. The atomic positions were
relaxed until the forces on the atoms were less than 0.04
eV/Å.
For the relaxed structure we calculated the theoretical
lattice constant. In Table 1 are shown the results of
geometry parameters (Figure 2) relaxed together with
the parameters corresponding to the ideal cylindrical
geometry obtained by rolling up the graphene plane. To
determine the magnitude of the translation vector (T) we
used the values 1.44 Å and 1.437 Å for ideal cylindrical
geometry and relaxed geometry, respectively. Hence, we
find that the lattice constant of the nanotubes in the di-
rection of the tube axis (z) changed by less than 0.3%
during the relaxation, in agreement with the trend indi-
cated by Machón et al. [12]. Also, the bonds and angles
in the direction of the tube axis and in the direction of the
circumference for the (8,8) and (14,0) nanotubes changed
by less than 0.3% with respect to the ideal structure.
Nevertheless, the bonds c and a for the (12,3) nanotube
experience changes by up to 10%. In the (12,3) nanotube
the bonds and angles tend to form a perfect hexagon for
the relaxed geometry and the sum of their three bond
angles is always smaller than 360˚ for all tubes.
Figure 2. Geometry parameters of the 1-nm-diameter na-
notubes.
Table 1. Geometry parameters for the ideal (i) rolled gra-
pheme sheet and for the relaxed (r) configuration. The pa-
rameters are defined as in Figure 2. T is the lattice constant.
T (Å) a (Å) b (Å) c (Å) α β γ
(8,8)-R 2.49 1.437 1.436 119.4 120.0
(8,8)-I 2.49 1.437 1.433 119.3 120.0
(14,0)-R 4.32 1.436 1.438 120.2 118.5
(14,0)-I 4.31 1.437 1.435 120.1 118.7
(12,3)-R 6.59 1.438 1.439 1.436 120.0 120.0118.7
(12,3)-I 6.59 1.389 1.335 1.597 112.5 115.9 130.0
In Table 1, we observe that the values of the relaxed
bond lengths are approximately the same for three nano-
tubes. Imtani & Jindal found three equal bond lengths
and three unequal bond angles in the structure of differ-
ent chiral tubes [41]. It is in agreement with the relaxed
bond length for the chiral tube (12,3). However, is in
disagreement with calculations obtained by Jiang et al.
[42], they found three unequal bond lengths in the struc-
ture of chiral (4,2) and (9,3) tubes. According to [41],
these differences were attributed to the unsatisfactory
reproduction of the graphite sheet bond length (1.42 Å)
from the beginning. On the other hand, Jiang et al. have
also found three unequal bond angles in the structure of
chiral (4,2) and (9,3) tubes. They obtained a value of β
larger than the ideal value and the other two bond angles
are smaller. Imtani & Jindal found three unequal bond
angles in the structure of different chiral tubes. Our re-
sults show bond angles very close to 120˚ for any nano-
tubes. We think that these differences could be related to
the radius of the nanotubes, i.e. our nanotubes do not
show effects of confinement.
The electronic band structures were calculated using
the relaxed geometries obtained above. The band struc-
tures obtained are given in Figure 3. The density of
states for the (8,8) and (12,3) tubes shown a metallic
character. This metallic character of both nanotubes is in
good agreement with the classification as metal 2p re-
ported by Saito et al. [4]. Experimental results also con-
firm the theoretical predictions about the metallicity of
the nanotube (8,8). Ouyang et al. [43] have reported the
tunneling spectrum of (8,8) nanotubes in bundles and
isolated. They have finding a gap-like feature at EF that is
not present in spectra of the isolated (8,8) armchair, in
good agreement with our result. Also, an ab initio
calculation recent on a armchair (7,7) nanotube (using
full potential-linarized augmented plane wave (FP-
LAPW) in the GGA approximation) shown that it is a
metallic nanotube with zero band gap and with the
valence and conduction bands cross each other at the
Fermi level [44], just as is observed in Figure 3 for (8,8)
and (12,3) nanotubes.
The nanotube (14,0) is clearly a semiconductor mate-
rial with a direct energy gap, as expected. This is consis-
tent with previous results obtained from ab initio code
VASP [45] and with the classification as semiconductor
type I given by Saito et al. [4].
In the Tight-Binding/Zone-Folding method, the transi-
tion energies between van Hove singularities in the elec-
tronic density of states is related to the diameter of the
tube by
0
2
ii cc
Enad=
02.9
γ
(1)
γ
= eV is the overlapping integral and where

J. MARQUINA ET AL.
AMPC
181
Figure 3. Calculated electronic band structures and DOS of the relaxed SWCNT’s. The Fermi level is at 0 eV. One thousand
k points for (8,8) nanotube and five thousand k points for (14,0) and (12,3) nanotubes were employed and the mesh cutoff was
at 1600 Ry for (8,8) nanotube and at 1200 Ry for (14,0) and (12,3) nanotubes.
1.437a=
()
112
224
cc Å (Table 1) is the carbon-carbon distance
mean of the nanotubes. The integer n has the values 1, 2,
4, 5 ... for the transitions E11, E22, E33, E44, of the semi-
conducting tubes, respectively, and 3, 6, ... for the tran-
sitions E11, E22, of the metallic tubes, respectively [46].
In Table 2 are shown electronic transition energies
(Eii). In this table is observed that the calculated values
for the gap energy (Eg) are in good agreement with the
previous report. On the contrary, the values for energies
E11 and E22 differ from values reported usign different
techniques. The energies Eii obtained from Zone-Folding
(Z-F) and Resonance Raman Spectroscopy (RRS) are
based in Tight-Binding approximation [46,47]. Thus, the
differences between our results and those obtained by
Z-F or RSS are due to the type of approximation used for
calculations of the energies Eii, i.e. Tight-Binding or
Density Functional Theory. On the other hand, they find
that the experimental values 1.45 and 2.73 eV for the (8,8)
nanotube shown in [43] are below our values. Although,
even the approach used is better than those obtained by
other methods, it does not reproduce well the valence
bands in the electronic band structure. This is a problem
inherent in all DFT-based methods.
Figure 4. Phonon dispersion curves. We have used used a
supercell with 160 atoms for the (8,8) nanotube and 162
atoms for the (14,0) nanotube. Seventy- five k points for (8,8)
nanotube and fifty k points for (14,0) and (12,3) nanotubes
were employed and the mesh cutoff was at 350 Ry for all
nanotubes.
Table 2. Energy-gap values and electronic transitions ener-
gies values.
The Figure 4 shows phonon dispersion curves of (8,8)
and (14,0) nanotubes. The phonon-dispersion curve for
(10,10) nanotube reported by Ye et al. [29] is very simi-
lar to the nanotube (8,8). And also, the dispersion curve
of (14,0) zigzag tube is in good qualitative agreement
with a dispersion curve for the (11,0) nanotube reported
in [29]. According to group theory there are eight modes
Raman active for an armchair carbon nanotube, with
symmetries and number of optically active phonon
modes given by [48]:
Eg (eV) E11 (eV) E22 (eV)
Our Rep.Our Rep. Our Rep.
(8,8) 0.00 0.00c 1.84 2.28a 2.22b, 1.45d 3.084.56a
2.73d
(14,0) 0.67 0.62e 0.67 0.76a 1.16 1.51a
(12,3) 0.00 0.00c 1.69 2.31a 2.04b 2.084.62a
aRef. [46]; bRef [47]; cRef. [4]; dRef. [43]; eRef. [45].
The A modes are non-degenerate and the E modes are
doubly degenerate.
g
gg
RA EEΓ=⊗ ⊗
1
3u
, (2)
()
I
In Table 3 we have assigned the symmetry of the dif-
ferent modes of vibration calculated to the (8,8) nanotube,
REΓ=. (3)

J. MARQUINA ET AL.
182
Table 3. Vibrational modes in zone center for (8,8) nano-
tubes. R and IR mean Raman-Active and infrar ed-active.
Symmetry
Our
Ab inicio
(GGA)
Ref. [29]
Ab initio
(LDA)
Ref. [54]
Tight-Binding
Ref. [49]
Exp.
E2g (R) 1603 1593 1698 1609
A1g (R) 1589 1580 1672 1593
E1u (IR) 1583 1574 1683 -
E1g (R) 1568 1561 1668 1567
following the assignment given in [29] taking into account
the Equations (2) and (3). In a recent paper presented
earlier by Rao et al. Raman bands were observed for an
isolated nanotube with chirality that are consistent with an
ensemble of (8,8), (9,9), (10,10), and (11,11) tubes [49].
They observed seven Raman peaks and failed to detect the
lowest frequency mode in the experiment because of the
strong Rayleigh scattering back- ground. These values are
used for comparison with our calculations. From Ta ble 3
is clear that in the high frequency region the calculations
made with the GGA approximation agree much better
with experiment than those using LDA or Tight-binding.
It is known that, the LDA and Tight-binding approxima-
tions tends to over estimate the high-energy phonons.
In the high-frequency region the phonon dipersions is
well reproduced in our calculations. For example, the
modes for A1g symmetry are 1589 and 1593 cm−1 for (8,8)
and (14,0) tubes, respectively. These values are just be-
low the highest frequency mode. On the other hand, tak-
ing into account that the strongest G band (assigned to
A1g symmetry [50,51]) at about 1590 cm−1 does not de-
pend on the tube diameter and that the G bands of the
outer tubes (in pristine DWCNT’s) fall in the same spec-
tral range as the G+ of an isolated semiconducting
SWCNT (1589 - 1593 cm−1) [30,52,53]. We conclude
that our results for the zone-center phonons in the high-
frequency region are in very good agreement with the
experimental values.
4. Conclusion
We have made a study of DFT as implemented in the
code SIESTA, using localized atomic wave functions as
a basis set with the GGA, and applied it to the study of
SWCNT’s about 1 nm in diameter. We found that the
structure for (8,8) and (14,0) nanotubes does not show
significant change compared with the rolled graphene
sheet, while the (12,3) nanotube shows significant change.
It has been observed a natural tendency to form regular
hexagons that dominates in the later case. Our results
predict that the electronic band structure for (8,8) and
(12,3) nanotubes has metallic behavior, that is, behaves
as metal at 0 K. Whereas the (14,0) nanotube is a semi-
conducting. Also, it is found that the accuracy of the
method for predicting the transition energies of Van
Hove singularities is insufficient. This is a problem in-
herent in DFT-based methods because it does not repro-
duce well the valence bands in the electronic band struc-
ture. Finally, we have shown that our results are compa-
rable with the experimental values, this proves that the
method used can be quite accurate for the high-energy
vibrations because of their reliable description of the
chemical bonds.
5. Acknowledgements
The authors are grateful to the PCP Carbon Nanotubes
(France)-MCT (Venezuela) for financial support. We
also would like to express our gratitude to Nicolas
RENON and the CALMIP (Calcul en Midi-Midi-Pyré-
nées) team for giving us access to the supercomputer
used for parallel computing. One of us (J. M.) would like
to thank Dr. L. Rincón for his interest in this work and
the useful suggestions.
REFERENCES
[1] S. Lijima, “Helical Microtubules of Graphitic Carbon,”
Nature, Vol. 354, 1991, pp. 56-58. doi:10.1038/354056a0
[2] N. Hamada, S.-I. Sawada and A. Oshiyama, “New One-
Dimensional Conductors: Graphitic Microtubules,” Phy-
sical Review Letters, Vol. 68, No. 10, 1992, pp. 1579-
1581. doi:10.1103/PhysRevLett.68.1579
[3] R. Saito, M. Fujita, G. Dresselhaus and M. S. Dresselhaus,
“Electronic Structure of Chiral Graphene Tubules,” Ap-
plied Physics Letters, Vol. 60, No. 18, 1992, pp. 2204-
2206. doi:10.1063/1.107080
[4] R. Saito, K. Sato, Y. Oyama, J. Jiang, G. G. Samsonidze,
G. Dresselhaus and M. S. Dresselhaus, “Cutting Lines
near the Fermi Energy of Single-Wall Carbon Nano-
tubes,” Physical Review B, Vol. 72, No. 15, 2005, Article
ID: 153413. doi:10.1103/PhysRevB.72.153413
[5] M. S. Dresselhaus, G. Dresselhaus and P. C. Ecklund,
“Science of Fullerene and Carbon Nanotubes,” Academic
Press, San Diego, 1996.
[6] P. J. F. Harris, “Carbon Nanotube Science,” Cambridge
University Press, London, 2009.
doi:10.1017/CBO9780511609701
[7] R. Saito, M. Fujita, G. Dresselhaus and M. S. Dresselhaus,
“Electronic Structure of Graphene Tubules Based on C60,”
Physical Review B, Vol. 46, No. 3, 1992, pp. 1804-1811.
doi:10.1103/PhysRevB.46.1804
[8] J. W. Mintmire and B. I. Dunlap, C. T. White. “Are
Fullerene Tubules Metallic?” Physical Review Letters,
Vol. 68, No. 5, 1992, pp. 631-634.
doi:10.1103/PhysRevLett.68.631
[9] R. Saito, T. Takeya, T. Kimura, G. Dresselhaus and M. S.
Dresselhaus, “Raman Intensity of Single-Wall Carbon
Nanotubes,” Physical Review B, Vol. 57, No. 7, 1998, pp.
4145-4153. doi:10.1103/PhysRevB.57.4145

J. MARQUINA ET AL. 183
[10] R. A. Jishi, L. Venkataraman, M. S. Dresselhaus and G.
Dresselhaus, “Symmetry Properties of Chiral Carbon Na-
notubes,” Physical Review B, Vol. 51, No. 16, 1995, pp.
11176-11179. doi:10.1103/PhysRevB.51.11176
[11] D. Sánchez-Portal, E. Artacho, J. M. Soler, A. Rubio and
P. Ordejón, “Ab Initio Structural, Elastic, and Vibrational
Properties of Carbon Nanotubes,” Physical Review B, Vol.
59, No. 19, 1999, pp. 12678-12688.
doi:10.1103/PhysRevB.59.12678
[12] M. Machón, S. Reich, C. Thomsen, D. Sánchez-Portal
and P. Ordejon, “Ab Initio Calculations of the Optical
Properties of 4-Å-Diameter Single-Walled Nanotubes,”
Physical Review B, Vol. 66, No. 15, 2002, Article ID:
155410. doi:10.1103/PhysRevB.66.155410
[13] K. Kanamitsu and S. Saito, “Geometries, Electronic Pro-
perties, and Energetics of Isolated Single Walled Carbon
Nanotubes,” Journal of the Physical Society of Japan,
Vol. 71, 2002, pp. 483-486. doi:10.1143/JPSJ.71.483
[14] V. N. Popov, “Curvature Effects on the Structural, Elec-
tronic and Optical Properties of Isolated Single-Walled
Carbon Nanotubes within a Symmetry-Adapted Non-
Orthogonal Tight-Binding Model,” New Journal of Phys-
ics, Vol. 6, 2004, pp. 1-17.
doi:10.1088/1367-2630/6/1/017
[15] S. Rols, Z. Benes, E. Anglaret, J. L. Sauvajol, P. Papanek,
J. E. Fischer, G. Coddens, H. Schober and A. J. Dianoux,
“Phonon Density of States of Single-Wall Carbon Nano-
tubes,” Physical Review Letters, Vol. 85, No. 24, 2000,
pp. 5222-5225. doi:10.1103/PhysRevLett.85.5222
[16] C. Thomsen, “Second-Order Raman Spectra of Single
and Multiwalled Carbon Nanotubes,” Physical Review B,
Vol. 61, No. 7, 2000, pp. 4542-4544.
doi:10.1103/PhysRevB.61.4542
[17] J. Maultzsch, S. Reich and C. Thomsen, “Chirality-Se-
lective Raman Scattering of the D Mode in Carbon
Nanotubes,” Physical Review B, Vol. 64, No. 12, 2001,
Article ID: 121407. doi:10.1103/PhysRevB.64.121407
[18] J. Maultzsch, J. S. Reich and S. C. Thomsen, “Raman
Scattering in Carbon Nanotubes Revisited,” Physical Re-
view B, Vol. 65, No. 23, 2002, Article ID: 233402.
doi:10.1103/PhysRevB.65.233402
[19] V. Zólyomi and J. Kiirti, “Calculating the Discrepancy
between the Stokes and Anti-Stokes Raman D Band of
Carbon Nanotubes Using Double Resonance Theory,”
Physical Review B, Vol. 66, No. 7, 2002, Article ID:
073418. doi:10.1103/PhysRevB.66.073418
[20] G. G. Samsonidze, R. Saito, A. Jorio, A. G. S. Filho, A.
Griineis, M. P. Pimenta, G. Dresselhaus and M. S. Dres-
selhaus, “Phonon Trigonal Warping Effect in Graphite
and Carbon Nanotubes,” Physical Review Letters, Vol. 90,
No. 2, 2003, Article ID: 027403.
doi:10.1103/PhysRevLett.90.027403
[21] G. L. Kane, E. J. Mele, R. S. Lee, J. E. Fischer, P. Petit, H.
Dai, A. Thess, R. E. Smalley, A. R. M. Verschueren, S. J.
Tans and G. Dekker, “Temperature-Dependent Resistivity
of Single-Wall Carbon Nanotubes,” EPL (Europhysics
Letters), Vol. 41, No. 6, 1998, pp. 683-689.
doi:10.1209/epl/i1998-00214-6
[22] Z. Yao, G. L. Kane and G. Dekker, “High-Field Electrical
Transport in Single-Wall Carbon Nanotubes,” Physical
Review Letters, Vol. 84, No. 13, 2000, pp. 2941-2944.
doi:10.1103/PhysRevLett.84.2941
[23] H. Suzuura and T. Ando, “Phonons and Electron-Phonon
Scattering in Carbon Nanotubes,” Physical Review B, Vol.
65, No. 23, 2002, Article ID: 235412.
doi:10.1103/PhysRevB.65.235412
[24] A. Sédéki, L. G. Caron and G. Bourbonnais, “Electron-
Phonon Coupling and Peierls Transition in Metallic Car-
bon Nanotubes,” Physical Review B, Vol. 62, No. 11,
2000, pp. 6975-6978. doi:10.1103/PhysRevB.62.6975
[25] Z. J. Q. Ding, Q. Jiang and D. Tian, “Vibrational Spec-
trum of Carbon Nanotubes,” Fullerene Science and Te-
chnology, Vol. 4, No. 1, 1996, pp. 31-37.
doi:10.1080/10641229608001535
[26] A. Charlier, E. McRae, M.-F. Charlier, A. Spire and S.
Forster, “Lattice Dynamics Study of Zigzag and Armchair
Carbon Nanotubes,” Physical Review B, Vol. 57, No. 11,
1998, pp. 6689-6696. doi:10.1103/PhysRevB.57.6689
[27] R. A. Jishi, L. Venkataraman, M. S. Dresselhaus and G.
Dresselhaus, “Phonon Modes in Carbon Nanotubules,”
Chemical Physics Letters, Vol. 209, No. 1-2, 1993, pp.
77-82. doi:10.1016/0009-2614(93)87205-H
[28] O. Dubay and G. Kresse, “Accurate Density Functional
Calculations for the Phonon Dispersion Relations of Gra-
phite Layer and Carbon Nanotubes,” Physical Review B,
Vol. 67, No. 3, 2003, Article ID: 035401.
doi:10.1103/PhysRevB.67.035401
[29] L. H. Ye, B. G. Liu, D. S. Wang and R. Han, “Ab Initio
Phonon Dispersions of Single-Wall Carbon Nanotubes,”
Physical Review B, Vol. 69, No. 23, 2004, Article ID:
235409. doi:10.1103/PhysRevB.69.235409
[30] E. Belandria, M. Millot, J. M. Broto, E. Flahaut, F. Rod-
riguez, R. Valiente and J. González, “Pressure Depend-
ence of Raman Modes in Double Wall Carbon Nanotubes
Filled with 1D Tellurium,” Carbon, Vol. 48, No. 9, 2010,
pp. 2566-2572. doi:10.1016/j.carbon.2010.03.036
[31] J. Marquina, E. Flahaut and J. González, “High-Pressure
Optical Absorption Studies of Double-Walled Carbon
Nanotubes,” Physica Status Solidi (RRL)—Rapid Research
Letters, Vol. 6, No. 9-10, 2012, pp. 382-384.
doi:10.1002/pssr.201206280
[32] D. Sánchez-Portal, P. Ordejón, E. Artachoa and J. M.
Soler, “Density-Functional Method for Very Large Sys-
tems with LCAO Basis Sets,” International Journal of
Quantum Chemistry, Vol. 65, No. 5, 1997, pp. 453-461.
doi:10.1002/(SICI)1097-461X(1997)65:5<453::AID-QU
A9>3.0.CO;2-V
[33] J. P. Perdew, K. Burke and M. Ernzerhof, “Generalized
Gradient Approximation Made Simple,” Physical Review
Letters, Vol. 77, No. 18, 1996, pp. 3865-3868.
doi:10.1103/PhysRevLett.77.3865
[34] N. Troullier and J. L. Martins, “Efficient Pseudopotentials
for Plane-Wave Calculations,” Physical Review B, Vol.
43, No. 3, 1991, pp. 1993-2006.
doi:10.1103/PhysRevB.43.1993
[35] J. Junquera, O. Paz, D. Sánchez-Portal and E. Artacho,
“Numerical Atomic Orbitals for Linear-Scaling Calcula-

J. MARQUINA ET AL.
184
tions,” Physical Review B, Vol. 64, No. 23, 2001, Article
ID: 235111. doi:10.1103/PhysRevB.64.235111
[36] J. Maultzsch, S. Reich, C. Thomsen, H. Requardt and P.
Ordejón, “Phonon Dispersion in Graphite,” Physical Re-
view Letters, Vol. 92, No. 7, 2004, Article ID: 075501.
doi:10.1103/PhysRevLett.92.075501
[37] M. Cardona, “In Electrons and Photons in Solids,” Scuola
Normale, Pisa, 2001.
[38] P. Pavone, R. Bauer, K. Karch, O. Schtt, S. Vent, W.
Windl, D. Strauch, S. Baroni and S. de Gironcoli, “Ab
Initio Phonon Calculations in Solids,” Physica B: Con-
densed Matter, Vol. 219-220, 1996, pp. 439-441.
doi:10.1016/0921-4526(95)00771-7
[39] J. Marquina, Ch. Power and J. González, “Espectroscopia
Raman del Grafeno Monocapa y el Grafito: Acopla-
miento Electrón Fonón y Efectos no Adiabáticos,” Re-
vista Tumbaga, Vol. 1, No. 5, 2010, pp. 183-194.
[40] Y. Miyamoto, M. L. Cohen and S. G. Louie, “Ab Initio
Calculation of Phonon Spectra for Graphite, BN, and
BC2N Sheets,” Physical Review B, Vol. 52, No. 20, 1995,
pp. 14971-14975. doi:10.1103/PhysRevB.52.14971
[41] A. N. Imtani and V. Jindal, “Structure of Chiral Single-
Walled Carbon Nanotubes under Hydrostatic Pressure,”
Computational Materials Science, Vol. 46, No. 2, 2009,
pp. 297-302. doi:10.1016/j.commatsci.2009.03.002
[42] H. Jiang, P. Zhang, B. Liu, Y. Huang, P. H. Geubelle, H.
Gao and K. C. Hwang, “The Effect of Nanotube Radius
on the Constitutive Model for Carbon Nanotubes,” Com-
putational Materials Science, Vol. 28, No. 3-4, 2003, pp.
429-442. doi:10.1016/j.commatsci.2003.08.004
[43] M. Ouyang, J. L. Huang, C. L. Cheung and C. M. Lieber,
“Energy Gaps in ‘Metallic’ Single-Walled Carbon Nano-
tubes,” Science, Vol. 292, No. 5517, 2001, pp. 702-705.
doi:10.1126/science.1058853
[44] H. S. Khadigeh, “Ab Initio Study of Electronic Properties
of a Armchair (7,7) Carbon Nanotube,” Advances in
Materials Physics and Chemistry, Vol. 2, 2012, pp. 159-
162. doi:10.4236/ampc.2012.23024
[45] T. Ito, K. Nishidate, M. Baba and M. Hasegawa, “First
Principles Calculations for Electronic Band Structure of
Single-Walled Carbon Nanotube under Uniaxial Strain,”
Surface Science, Vol. 514, No. 1-3, 2002, pp. 222-226.
doi:10.1016/S0039-6028(02)01633-3
[46] M. Hulman, R. Pfeiffer and H. Kuzmany, “Raman Spec-
troscopy of Small-Diameter Nanotubes,” New Journal of
Physics, Vol. 6, 2004, pp. 1-17.
doi:10.1088/1367-2630/6/1/001
[47] C. Fantini, A. Jorio, M. Souza, M. S. Strano, M. S. Dres-
selhaus and M. A. Pimenta, “Optical Transition Energies
for Carbon Nanotubes from Resonant Raman Spectros-
copy: Environment and Temperature Effects,” Physical.
Review Letters, Vol. 93, No. 14, 2004, Article ID: 147406.
doi:10.1103/PhysRevLett.93.147406
[48] O. E. Alon, “Number of Raman- and Infrared-Active Vi-
brations in Single-Walled Carbon Nanotubes,” Physical
Review B, Vol. 63, No. 20, 2001, Article ID: 201403.
doi:10.1103/PhysRevB.63.201403
[49] A. M. Rao, E. Richter, S. Bandow, B. Chase, P. C. Ek-
lund, K. A. Williams, S. Fang, K. R. Subbaswamy, M.
Menon, A. Thess, R. E. Smalley, G. Dresselhaus and M.
S. Dresselhaus, “Diameter-Selective Raman Scattering
from Vibrational Modes in Carbon Nanotubes,” Science,
Vol. 275, No. 5297, 1997, pp. 187-191.
doi:10.1126/science.275.5297.187
[50] H. D. Sun, Z. K. Tang, J. Chen and G. Li, “Polarized
Raman Spectra of Single-Wall Carbon Nanotubes Mono-
Dispersed in Channels of ALPO4-5 Single Crystals,”
Solid State Communications, Vol. 109, No. 6, 1999, pp.
365-369. doi:10.1016/S0038-1098(98)00588-2
[51] C. Thomsen, “Second-Order Raman Spectra of Single
and Multiwalled Carbon Nanotubes,” Physical Review B,
Vol. 61, No. 7, 2000, pp. 4542-4544.
doi:10.1103/PhysRevB.61.4542
[52] A. Jorio, A. G. Souza Filho, G. Dresselhaus, M. S. Dres-
selhaus, A. K. Swan, M. S. Ünlü, B. B. Goldberg, M. A.
Pimenta, J. H. Hafner, C. M. Lieber and R. Saito, “G-
Band Resonant Raman Study of 62 Isolated Single-Wall
Carbon Nanotubes,” Physical Review B, Vol. 65, No. 15,
2002, Article ID: 155412.
doi:10.1103/PhysRevB.65.155412
[53] M. Dresselhaus, G. Dresselhaus, R. Saito and A. Jorio,
“Raman Spectroscopy of Carbon Nanotubes,” Physics
Reports, Vol. 409, No. 2, 2005, pp. 47-99.
doi:10.1016/j.physrep.2004.10.006
[54] D. Kahn and J. P. Lu, “Vibrational Modes of Carbon
Nanotubes and Nanoropes,” Physical Review B, Vol. 60,
No. 9, 1999, pp. 6535-6540.
doi:10.1103/PhysRevB.60.6535