Paper Menu >>
Journal Menu >>
 J. Mod. Phys., 2010, 1, 276-280 doi:10.4236/jmp.2010.14038 Published Online October 2010 (http://www.SciRP.org/journal/jmp) Copyright © 2010 SciRes. JMP Observation of Superluminal in Doppler Broadened Two-Level Atomic Systems in Magnetic Field Shuangqiang Liu, Yundong Zhang*, Hao Wu, Ping Yuan Institute of Opto-Electronics an d National Key Laboratory of Tunable Laser Tech nology, Harbin Institute of Technology, Harbin, China E-mail: *Ydzhang02@yahoo.com.cn Received June 23, 2010; revised July 23, 2010; acc epted July 28, 2010 Abstract A novel method to control the group velocity of light propagation in a two-level atomic system without addi- tional optical field is proposed. Numerical result and experimental data shows that by changing the magnetic field intensity and vapor temperature, the group velocity of probe light can be controlled in an appropriate region. Keywords: Multiphoton Processes, Atom Optics, Hyperfine Structure, Zeeman Effect 1. Introduction Recently, the precise control of group velocity of light propagation has made many progresses in both sublu- minal and superluminal. Slow light propagation can be achieved by using the techniques of electromagnetically induced transparency (EIT) [1-4], coherent population oscillations (CPO) [5-6], coherent hole burning (CHB) [7-8], two-wave mixing [9], stimulated Brillouin scatter- ing (SBS) [10], stimulated Raman scattering (SRS) [11], and so on. In superluminal area Brillouin showed theo- retically that inside an absorption line the dispersion is anomalous, which resulted in a group velocity faster than c in 1960 [12], and negative group velocity of –c/(300 + 30) in Cs atom vapor was found in 2000 [13]. After their works Bigelow et al. realized the transition from super- luminal to subluminal propagation in alexandrite crystal at room temperature [6]. Agarwal and Dey put forward their theoretical discussion about sub- and superluminal propagations in saturated and reverse saturated absorp- tion (RSA) materials [14]. By using this method, our lab had observed superluminal in C60 solution [15] and er- bium-doped fiber [16]. These methods show the possibil- ity to control the group velocity of light, however, there are some drawbacks in these schemes, in which strong couple field is needed (EIT, CHB) or some very special levels structure is required (CPO, RSA), or which only works in fiber (SBS, SRS), what make these schemes difficult to be realized in different situations. In this paper we give a proposal which can be used to change the group velocity of probe field by controlling the intensity of magnetic field and atomic vapor tem- perature. It is well known that energy levels will split in magnetic field because of Zeeman Effect, so the absorp- tion characteristic of the medium will change, what leads to the alteration of the group velocity of the probe light. We theoretically put forward the variation of the group velocity of the probe light when it propagates though an atomic vapor under magnetic field, and observed the time advance experimentally. Our results should be helpful to realize light propagation in Doppler-broadened atomic systems. 2. Theory and Equations It is assumed that the magnetic field is homogeneous within the atomic vapor and that the incident linearly polarized radiation is transverse to the magnetic field, therefore the polarization can be resolved into equal am- plitude left-hand and right-hand circularly polarized com- ponents. For an atom with a total electron angular mo- mentum J, nuclear spin I, total angular momentum F = I + J, and projection of the total angular momentum along the direction of the external magnetic field M, the Ham- iltonian matrix elements (F,F’) for each value of M are [17]  S. Q. LIU ET AL. Copyright © 2010 SciRes. JMP 277 1/2 1 ', '1121212'1 11' '0 MJ I FjI IJFMHIJF MEF FBggJJJFF JJFF FIFMM (1) here the first term represents the hyperfine interaction energy, the second represents the external magnetic energy, μ is the Bohr magneton, B is the external mag- netic field, j g and I g are the gyromagnetic factors for the total orbital angular momentum and nuclear spin momentum, respectively. The matrix element de- pendence on M is contained within a 3-j symbol (en- closed by the brackets), and the matrix element depend- ence on F is related to a 6-j symbol (enclosed by the braces). 1.51 211 1 2221221 F KKII JJ EhAKhB II JJ (2) with 111KFF JJ IIand A and B are the magnetic dipole and electric quadruple constants for the energy level of interest, respectively. In the following, the response of the atomic system to the applied field is to be discussed by defining the sus- ceptibility . Taken into account the contribution from each hyperfine component, the susceptibility can be expressed as: 2 '' 00 22 ,' ' '' 32 ' ,,'' 21 4 1' 212'1 1' '1' FF MMeD nFM F M FF MM In efJJ FMF MiJ mv FFJIF NF FW MMFJ (3) Here ,' ' () FM F M W is the plasma dispersion function, 2 ,' ' ,'' 2/ x FM F M DFMFM ie Wdx xIn i (4) with is the wavelength and is the lifetime of the excited level. (' ) f JJ is absorption oscillator strength from the ground state to excited state. D is the Doppler width, which can be calculated by 2 22 DkT In cM (5) n N is the population density of the ground-state Zee- man level M (assuming that the optical pumping is neg- ligible), there is 0 exp exp FM nFM h kT NN h kT (6) 0 N is the atomic density of 1/2 6S, given by [18]. The group velocity and the group refractive index can be given by: Re 12Re 2 gg cc n (7) 3. Numerical Results and Discussion Basing on the above formulas in the previous section, we take Cs 2 D transition (1/23/2 6( 4)6SF P ) for exam- ple, and summarize our results for the steady state be- havior of the system. Because the Doppler width (about 379 MHz at 303 K) is far larger than the splitting be- tween the sub-levels of 3/2 6P at room temperature, the sub-levels of 3/2 6P (F = 3, 4, 5) can’t be differentiated in this situation. For the transition 1/23/2 6( 4)6SF P , based on the selection rule for electric dipole transition (0,F 1, 1m ), there are twenty-four left-hand and right-hand transition, respectively. By using Equation 3 and taking into account the contribution from each hyperfine com- ponent, we show the behaviors of real and imaginary parts of the susceptibility in Figure 1(a) and Figure 1(b), respectively. It’s well known that the imaginary and real part of the susceptibility reflect the absorption and dispersive prop- erty of the medium, respectively. As is shown in Figure 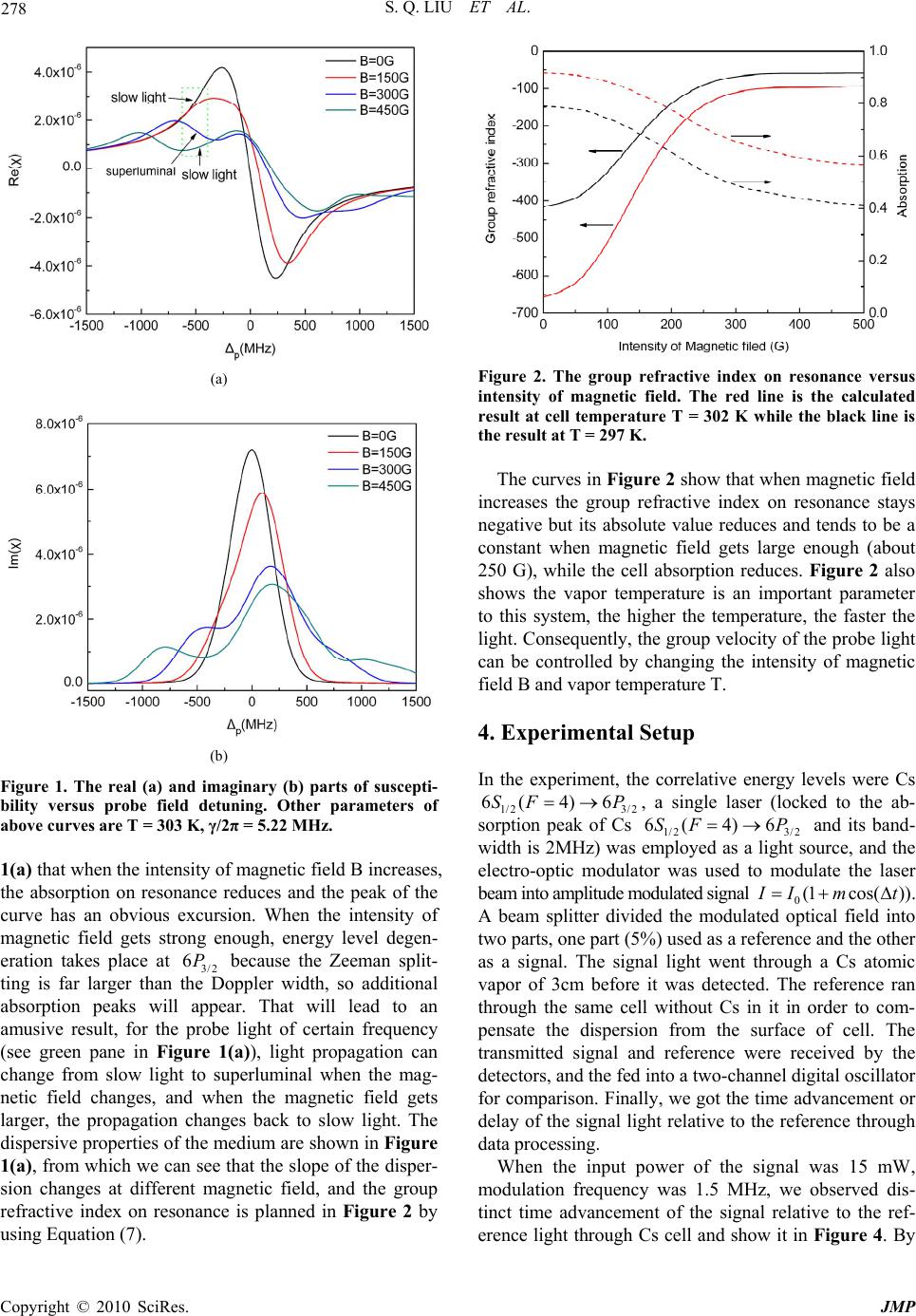 S. Q. LIU ET AL. Copyright © 2010 SciRes. JMP 278 (a) (b) Figure 1. The real (a) and imaginary (b) parts of suscepti- bility versus probe field detuning. Other parameters of above curves are T = 303 K, γ/2π = 5.22 MHz. 1(a) that when the intensity of magnetic field B increases, the absorption on resonance reduces and the peak of the curve has an obvious excursion. When the intensity of magnetic field gets strong enough, energy level degen- eration takes place at 3/2 6P because the Zeeman split- ting is far larger than the Doppler width, so additional absorption peaks will appear. That will lead to an amusive result, for the probe light of certain frequency (see green pane in Figure 1(a)), light propagation can change from slow light to superluminal when the mag- netic field changes, and when the magnetic field gets larger, the propagation changes back to slow light. The dispersive properties of the medium are shown in Figure 1(a), from which we can see that the slope of the disper- sion changes at different magnetic field, and the group refractive index on resonance is planned in Figure 2 by using Equation (7). Figure 2. The group refractive index on resonance versus intensity of magnetic field. The red line is the calculated result at cell temperature T = 302 K while the black line is the result at T = 297 K. The curves in Figure 2 show that when magnetic field increases the group refractive index on resonance stays negative but its absolute value reduces and tends to be a constant when magnetic field gets large enough (about 250 G), while the cell absorption reduces. Figure 2 also shows the vapor temperature is an important parameter to this system, the higher the temperature, the faster the light. Consequently, the group velocity of the probe light can be controlled by changing the intensity of magnetic field B and vapor temperature T. 4. Experimental Setup In the experiment, the correlative energy levels were Cs 1/23/2 6( 4)6SF P , a single laser (locked to the ab- sorption peak of Cs 1/2 3/2 6( 4)6SF P and its band- width is 2MHz) was employed as a light source, and the electro-optic modulator was used to modulate the laser beam into amplitude modulated signal 0(1cos( )) I Im t . A beam splitter divided the modulated optical field into two parts, one part (5%) used as a reference and the other as a signal. The signal light went through a Cs atomic vapor of 3cm before it was detected. The reference ran through the same cell without Cs in it in order to com- pensate the dispersion from the surface of cell. The transmitted signal and reference were received by the detectors, and the fed into a two-channel digital oscillator for comparison. Finally, we got the time advancement or delay of the signal light relative to the reference through data processing. When the input power of the signal was 15 mW, modulation frequency was 1.5 MHz, we observed dis- tinct time advancement of the signal relative to the ref- erence light through Cs cell and show it in Figure 4. By  S. Q. LIU ET AL. Copyright © 2010 SciRes. JMP 279 Figure 3. Experiment setup for Cs superluminal observation. Figure 4. The waveform of a 1.5 MHz amplitude modulated signal propagating through 3 cm empty cell (black line), 3 cm Cs cell without magnetic field on (blue line), and 3 cm cell in 300 G magnetic field (red line) at room temperature T = 293 K. Figure 5. Observed time advancement (solid dot) and theo- retically calculated result (red line) as a function of the in- tensity of magnetic field at room temperature T = 293 K. using (1) / adv g tLnc , we got 299 g n (B = 0) and 179 g n (B = 300 G). Figure 5 displays the time ad- vancement as a function of the magnetic field, form which Figure 6. Observed time advancement (solid dot) and theo- retically calculated result (black line) as a function of the cell temperature at the intensity of magnetic field B = 200 G. we can see clearly that by changing the magnetic field, the time advancement can be controlled in an appropriate region. Figure 6 shows the pulse passes faster because more atoms are provided to the system when the cell temperature is higher. 5. Conclusion In conclusion, superluminal in Doppler broadened two level atomic systems under magnetic field was theoreti- cally brought forward, and observed in experiment. It is shown that both the group refractive index and vapor absorption depend on the magnetic field intensity and vapor temperature. By only changing those parameters, the group velocity of light can be controlled in an appro- priate region, and our work should be helpful to realize superluminal propagation in various Doppler-broadened atomic systems. 6. Acknowledgements The research is supported by the National Natural Sci- ence Foundation of China under Grant Nos. 60272075, 60478014 and 60878006, the National High Technology Research and Development Program (“863” Program) of China under Grant No. 2007AA12Z112. 7. References [1] S. E. Harris, “Electromagnetically Induced Transpar- ency,” Physics Today, Vol. 50, No. 7, 1997 pp. 36-42. [2] J. P. Marangos, “Topical Review Electromagnetically Induced Transparency,” Journal of Modern Optics, Vol. 45, No. 3, 1998, pp. 471-503. [3] J. G. Banacloche, Y. Li, S. Jin and M. Xiao, “Observation  S. Q. LIU ET AL. Copyright © 2010 SciRes. JMP 280 of an Electromagnetically Induced Change of Absorption in Multilevel Rubidium Atoms,” Physical Review A, Vol. 51, No. 3, 1997, pp. R1754-R1757. [4] M. Fleischhauer, A. Imamoglu and J. P. Marangos, “Electromagnetically Induced Transparency: Optics in Coherent Media,” Reviews of Modern Physics, Vol. 77, No. 2, 2005, pp. 633-678. [5] M. S. Bigelow, N. N. Lepeshkin and R. W. Boyd, “Ob- servation of Ultraslow Light in a Ruby Crystal at Room Temperature,” Physical Review Letters, Vol. 90, No. 11, 2003, p. 113903. [6] M. S. Bigelow, N. N. Lepeshkin and R. W. Boyd, “Su- perluminal and Slow Light Propagation in a Room-Tem- perature Solid,” Science, Vol. 301, No. 5630, 2003, pp. 200-202. [7] P. Dong and J. Y. Gao, “Appearance and Disappearance of Hole-Burrning behind an Electromanetically Induced Transparency Window,” Physical Letter A, Vol. 265, No. 1-2, 2000, pp. 52-57. [8] J. H. Wu, X. G. Wei, D. F. Wang, Y. Chen and J. Y. Gao, “Coherent Hole-Burning Phenomenon in a Doppler Braod- ened Three-Level-Type Atomic System,” Journal of Op- tics B, Vol. 6, No. 1, 2004, pp. 54-58. [9] E. Podivilov, B. Sturman, A. Shumelyuk and S. Odoulov, “Light Pulse Slowing down up to 0.025 Cm/S by Pho- torefractive Two-Wave Coupling,” Physical Review Let- ters, Vol. 91, No. 8, 2003, p. 83902. [10] K. Y. Song, M. G. Herraez and L. Thevenaz, “Gain-As- sisted Pulse Advancement Using Single and Double Bril- louin Gain Peaks in Optical Fibers,” Optic Express, Vol. 13, No. 24, 2005, pp. 9758-9765. [11] J. Q. Liang, M. Katsuragawa, F. L. Kien and K. Hakuta, “Slow Light Produced by Stimulated Raman Scattering in Solid Hydrogen,” Physical Review A, Vol. 65, No. 3, 2002, p. 31801. [12] L. Brillouin, “Wave Propagation and Group Velocity,” Academic Press, New York, 1960. [13] L. J. Wang, A. Kuzmich and A. Dogariu, “Gain-Assisted Superluminal Light Propagation,” Nature, Vol. 406, No. 6793, 2000, pp. 277-283. [14] G. S. Agarwal and T. N. Dey, “Sub- and Superluminal Propagation of Intense Pulses in Media with Saturated and Reverse Absorption,” Physical Review Letters, Vol. 92, No. 20, 2004, p. 203901. [15] H. Wang, Y. D. Zhang, N. Wang, W. L. Yan, H. Tian, W. Qiu and P. Yuan, “Observation of Superluminal Propaga- tion at Negative Group Velocity in C60 Solution,” Ap- plied Physics Letters, Vol. 90, No. 12, 2007, p. 121107. [16] H. Wang, Y. D. Zhang, L. Ma, Z. S. He, H. Tian and P. Yuan, “Experimental Observation of Negative Group Veloc- ity in C-60 PMMA,” OPTIK, Vol. 120, No. 13, 2009, pp. 673-675. [17] B. Yin and T. M. Shay, “Theoretical Model for a Faraday Anomalous Dispersion Optical Filter,” Optical Letters, Vol. 16, No. 20, 1991, pp. 1617-1619. [18] Daniel A. Steck, Cesium D Line Data, 1998. http://stech.us/alkalidata |

