J. Mod. Phys., 2010, 1, 244-250
doi:10.4236/jmp.2010.14036 Published Online October 2010 (http://www.SciRP.org/journal/jmp)
Investigation of Neutrino-Nucleon Interaction through
Intermediate Vector Boson (IVB)
Mohamed Tarek Hussein1, Ahmad Islam Saad2
1Physics Department, Faculty of Science, Cairo University, Giza, Egypt
2Physics an d Chemistr y Departme nt, Faculty of Education, Alexandria University, Alexandria, Egypt
Received July 15, 2010; revised August 18, 2010; accepted August 12, 2010
Abstract
This work deals with the interaction of neutrino with the nucleon considering data taken from different ex-
periments. It is assumed that the interaction of neutrino with nucleons go through the intermediate vector
boson (IVB) which may be the W or Z with effective mass of the order of 80 GeV. The neutrino wave func-
tion is obtained via perturbation technique to calculate the weak leptonic current. On the other hand, the
quark current is estimated using the measured experimental data of deep inelastic scattering of neutrino-nucleon
interaction. Eventually the total interaction transition matrix is calculated as a function of momentum transfer
square, q2 and qualitatively compared with the available experimental data. Besides, a comparative study is
also done to explore the influence of the target composition during the neutrino weak interactions. In this
context an investigation of neutrino-proton and neutrino-neutron interactions are carried out to calculate the
deep inelastic cross section in both cases.
Keywords: Deep Inelastic Scattering (DIS), Intermediate Vector Boson (IVB), Parton Model, Structure Function
1. Introduction
The problem of weak interactions through the charged
and neutral currents is dealt by many different ap-
proaches. A classical picture of lepton neutral current by
James L. Carr [1] considered that, when charged current
weak interactions are excluded, the neutral current weak
interaction is formally similar to ordinary electromagnet-
ism with a massive photon. In this spirit, the Maxwell
equations for the fields of the Z-boson are derived from
the standard model. For neutral current events, electrons
(or neutrinos) remain as electrons (or neutrinos).
In the charged current case, an initial electron state
emerges as a final neutrino state or vice-versa. For this
reason it is difficult to consider such a picture for the
charged current interaction. A non-relativistic weak-field
Hamiltonian for the electron is developed which allows
computing the interaction energy of an electron in the
presence of a classical Z-boson field. The Maxwell equa-
tions for the Z-boson are then developed. In the absence
of sources, the Maxwell equations, [2] are identical to
those of ordinary electromagnetism but with a massive
photon. The Maxwell equation source terms are derived
from the interaction energies for both electron and neu-
trino sources. The Maxwell equations derived in this case
can be used to describe the Z-boson field generated by
macroscopic or atomic-scale. They may also be used to
visualize the Z-boson fields surrounding classical point-
like electrons and neutrinos. The classical point particle
solutions provide an interesting visualization of the par-
ity violation in the standard model in terms of a vor-
tex-like magnetic field structure oriented with the elec-
tron’s spin.
In calculating the cross section of neutrino nucleon in-
teractions, we consider the three independent helicity
states (–1,+1,0) for the mediating bosons W±. In the
weak interactions there is no conservation of parity
which compels helicity –1 and +1 states to occur with
equal probability as a coherent superposition as in elec-
tromagnetic case. Thus for e-nucleon interactions we
need 2-structure functions (F1 and F2) to describe the
inelastic cross section while 3-structure functions (F1, F2
and F3) are needed for neutrino nucleon interactions.
2. Background
An alternative method was developed by T. Siiskonen et
al., [3], where the phenomenological structure of the

M. T. HUSSEIN ET AL.
245
weak hadronic current between the proton and neutron
states is well determined by its properties under the Lor-
entz transformation. Additional constraints come from
the requirement of time reversal symmetry as well as
from the invariance under the G-parity transformation
(combined charge conjugation and isospin rotation). The
resulting interaction Hamiltonian consists of vector (V),
axial vector (A), induced weak magnetism (M), and in-
duced pseudoscalar (P) terms together with the associ-
ated form factors C,  = V, A, M, or P. These form fac-
tors are called as coupling constants at zero momentum
transfer. The present experimental knowledge does not
exclude the presence of the scalar and tensor interactions.
However, their contribution is expected to be small due
to weak coupling [4]. The values of vector, axial vector,
and weak magnetism couplings are well established by
beta-decay experiments as well as by the conserved vec-
tor current hypothesis (CVC), introduced already in the
late 50’s [5]. The magnitude of the pseudoscalar cou-
pling is more uncertain, although the partially-conserved
axial current hypothesis (PCAC) [6] provides an estimate
along with muon capture experiments in hydrogen [7,8].
In nuclear beta decay, with an energy release up to some
20 MeV, only the vector (Fermi) and the axial vector
(Gamow-Teller) terms are usually important. The in-
duced pseudoscalar and weak magnetism parts are essen-
tially inactive, since their contributions are proportional
to q /M, where q is the energy release and M is the nu-
cleon mass (in units where ħ = c = 1).
T. Siiskonen et al., [9,10] constructed effective opera-
tors for the weak hadronic current between proton and
neutron states. These operators take into account the core
polarization effects, which are expected to be the largest
correction to the bare matrix element [11].
As mentioned earlier, Fermi conceived of
 -decay as a
process analogous to that of an electromagnetic transition,
the electron-neutrino (e-) pair are playing the role of the
emitted photon. The amplitude was assumed to involve,
for the nucleons, the hadronic weak current matrix ele-
ment <p|J|n >, in analogy to the electromagnetic transi-
tion currents. A simple Lorentz invariant amplitude is
then obtained if e pair also appears as a 4-vector com-
bination <e|J|O>, which is the leptonic weak current
matrix element. The complete matrix element being, M =
<p|J|n> <e|J|O>. At very low energy release, one
might expect that, to a good approximation, all momen-
tum dependence in the matrix element could be ignored,
reducing it to a constant G = 1.14 × 10-5 GeV-2, in the
natural units (ħ = c = 1). The first statement of universal-
ity of weak interactions was that all processes have the
same coupling constant G. Fermi's vector-vector theory
was motivated by the analogy of the vector currents of
QED. The analogy was however, imperfect. The photon
emitted in a radioactive transition is the quantum of the
electromagnetic field, but it is hard to see how the corre-
sponding e  pair can be the weak field quantum, since
the effective mass of the pair varies from process to an-
other. It is therefore natural to postulate the existence of
a weak analogue of the photon-the intermediate vector
boson (IVB) and to suppose that weak interactions are
mediated by the exchange of IVB’s as the electromag-
netic ones are by photon exchange. This was the first
step toward an eventual unification at the weak and elec-
tromagnetic fields. In the presence of currents, the wave
equation for the photon has the form:
em
A
j


 (1)
The propagator associated to the process is just the
inverse of the differential operator in Equation (1). Ap-
plying this to the free particle, we get 2em
qA j


,
hence the propagator is 2
g
q

. As for a massive
spin-1 particle, in a general gauge, the Maxwell equa-
tions read
A
Aj

 


 (2)
We make the natural replacement □  (□ + M2) to
get,
(□2)
M
WWj

 


  (3)
For plane-wave solution,
22
[( )]qMgqqWj

 


  . And the propagator is
expected in this case to correspond to the inverse opera-
tor 22 1
[( )]qMg qq
  
 which may be written in
the form of
A
gBqq



. The values of the constants
A and B are found from the matrix identity 11MM

,
hence, 22 [()] ()
p
p
qMg qqAg Bqq

 


 .
Then, 22
1( )AqM  and 22 2 1( )BMqM
.
This leads to the propagator form
2
22
/
g
qq M
qM
 

.
Then the total transition matrix element has the form:
2
22
wk wk
gqqM
M
JJ
qM
 







(4)
Furthermore, a series of celebrated experiments [12-14]
have shown that neutrinos have the following properties:
1) They are massless or nearly so in the standard
model viewpoint.
2) There are three distinct types of neutrino each is
associated with its own charged lepton: (e-,e), (-,)
and (-,).
3) They have spin 1/2 but only the negative helicity
state (left-handed) participates in weak interactions.
4) The weak interactions don't conserve P, the parity,
not do they respect invariance under the charge conjuga-
tion.

M. T. HUSSEIN ET AL.
246
The study of the Lorentz covariance of Dirac equa-
tions defines the vector current as uu


and the axial
vector current as 5 uu


 , where u is a 4-component
wave function and 5 is a 4 × 4 matrix that defined in
terms of the Dirac  matrices as: 0123
5i

 . Writ-
ing the parity operator P in the form 10
01
P 


, then
it is possible to show that the vector current Vuu



transforms under parity as 00 0 (, )Vu uVV

 ,
while the axial vector 5
A
uu


  transforms to
050
A
uu


 , or in other words 0 (,)
A
AA

 .
The right and left-handed helicity operators PR, PL are
defined as 5
1
2
R
P





and 5
1
2
L
P





, which
satisfy the relations, 2
L
L
PP,2
R
R
PP,0
LR RL
PP PP,
1
LR
PP. So that, for massless spin 1/2 neutrinos, the
combination 5 (1)( )up


 contains only a left-handed
component.
Instead of pure vector currents, we have now the vec-
tor V, and axial vector, A, pieces. The leptonic weak
current for each lepton and its neutrino has the form,





5
''
1
2'' 1
2
wk
JJ
gNNu u


 
 



(5)
where g, is the coupling constant for the W(Z) boson that
exchanges in weak processes. The total interaction ma-
trix element contains both the leptonic current and the
hadronic or the quark current, written as:





2
2
522
5
1
2' 1
2
1
(')(1 )()
2
Z
Z
ji
ij
gqqM
Mg uuqM
uq uq
 


 







(6)
where q refers to the quark type u, d, s,….
3. Problem Statement
A model for weak interaction of neutrino with nucleons
is proposed. In this model we assume that the neutrino
interacts with nucleons through the IVB which may be
the W or Z with effective mass about 80 GeV. The
Feynman diagram as in Figure 1 represents the interac-
tion.
The scattering amplitude is then calculated according
to Equation (6). The implementation of this equation
reveals two main problems. The first of them is latent in
the calculation of neutrino wave function to calculate the
weak leptonic current. The second one comes in calcu-
lating the quark hadronic current, which consequently



hadronns
N
q2
Figure 1. Feynman repre sentation of the -nucleon interac-
tion.
needs the specification of the wave function of the
quarks forming the nucleon.
4. Results and Discusion
As mentioned earlier Equation (5), the weak leptonic
current is calculated as:

  
5
1
'2''1
2
wk
JgNN






  (7)
where ()&(')

 , are the neutrino wave functions
before and after scattering at the first vertex of Figure 1.
As a good approximation, it is possible to consider the
neutrino’s wave function as a plane wave with the form:

 .
,ikr t
jj
rt ue


 (8)
The 4-component matrix u describes the spin 1/2 par-
ticle:
1
0
z
xy
P
uEm
PiP
Em
















(9)
Since the neutrino is massless and moves initially in
the z-direction so,















0
1
0
1
u.
On the other hand, we used the perturbation technique
to find the scattered wave function of the neutrino as: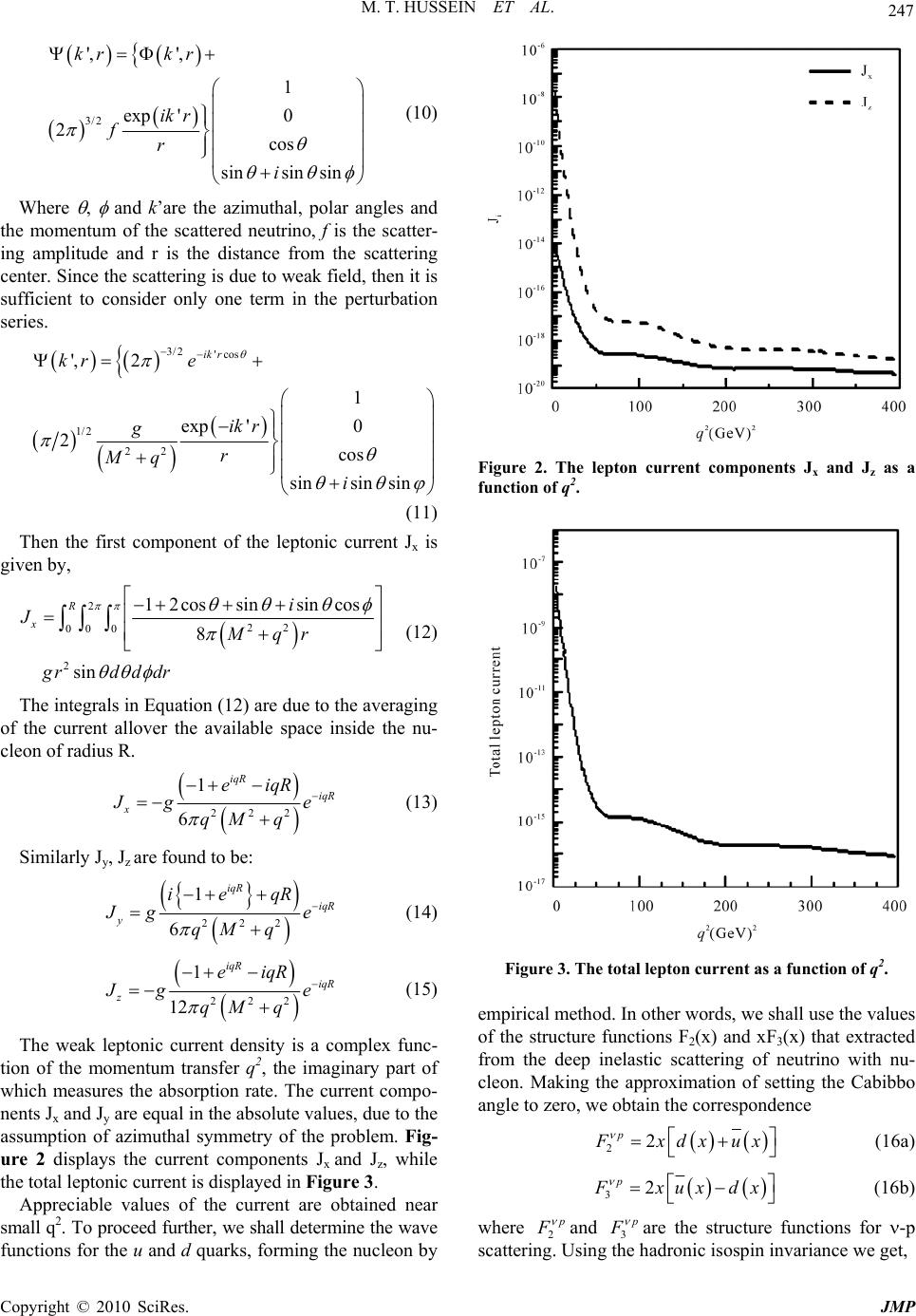

M. T. HUSSEIN ET AL.
247
  
 
3/ 2
', ',
1
exp '0
2cos
sinsin sin
kr kr
ik r
fr
i













(10)
Where
 ,  and k’are the azimuthal, polar angles and
the momentum of the scattered neutrino, f is the scatter-
ing amplitude and r is the distance from the scattering
center. Since the scattering is due to weak field, then it is
sufficient to consider only one term in the perturbation
series.





3/2 'cos
1/2
22
', 2
1
exp '0
2cos
sinsin sin
ik r
kr e
ik r
g
r
Mq
i






 









(11)
Then the first component of the leptonic current Jx is
given by,

2
22 00 0
2
12cos sinsincos
8
sin
R
xi
JMqr
grd d dr







 




  (12)
The integrals in Equation (12) are due to the averaging
of the current allover the available space inside the nu-
cleon of radius R.


222
1
6
iqR
iqR
x
eiqR
J
ge
qM q 

 
  (13)
Similarly Jy, Jz are found to be:
 

222
1
6
iqR
iqR
y
ieqR
J
ge
qM q 


 (14)


222
1
12
iqR
iqR
z
eiqR
J
ge
qM q 

 
  (15)
The weak leptonic current density is a complex func-
tion of the momentum transfer q2, the imaginary part of
which measures the absorption rate. The current compo-
nents Jx and Jy are equal in the absolute values, due to the
assumption of azimuthal symmetry of the problem. Fig-
ure 2 displays the current components Jx and Jz, while
the total leptonic current is displayed in Figure 3.
Appreciable values of the current are obtained near
small q2. To proceed further, we shall determine the wave
functions for the u and d quarks, forming the nucleon by
Figure 2. The lepton current components Jx and Jz as a
function of q2.
Figure 3. The total lepton current as a function of q2.
empirical method. In other words, we shall use the values
of the structure functions F2(x) and xF3(x) that extracted
from the deep inelastic scattering of neutrino with nu-
cleon. Making the approximation of setting the Cabibbo
angle to zero, we obtain the correspondence
 
22
p
F
xdx ux





 (16a)
 
32
p
F
xux dx





 (16b)
where 2
p
F

and 3
p
F

are the structure functions for -p
scattering. Using the hadronic isospin invariance we get,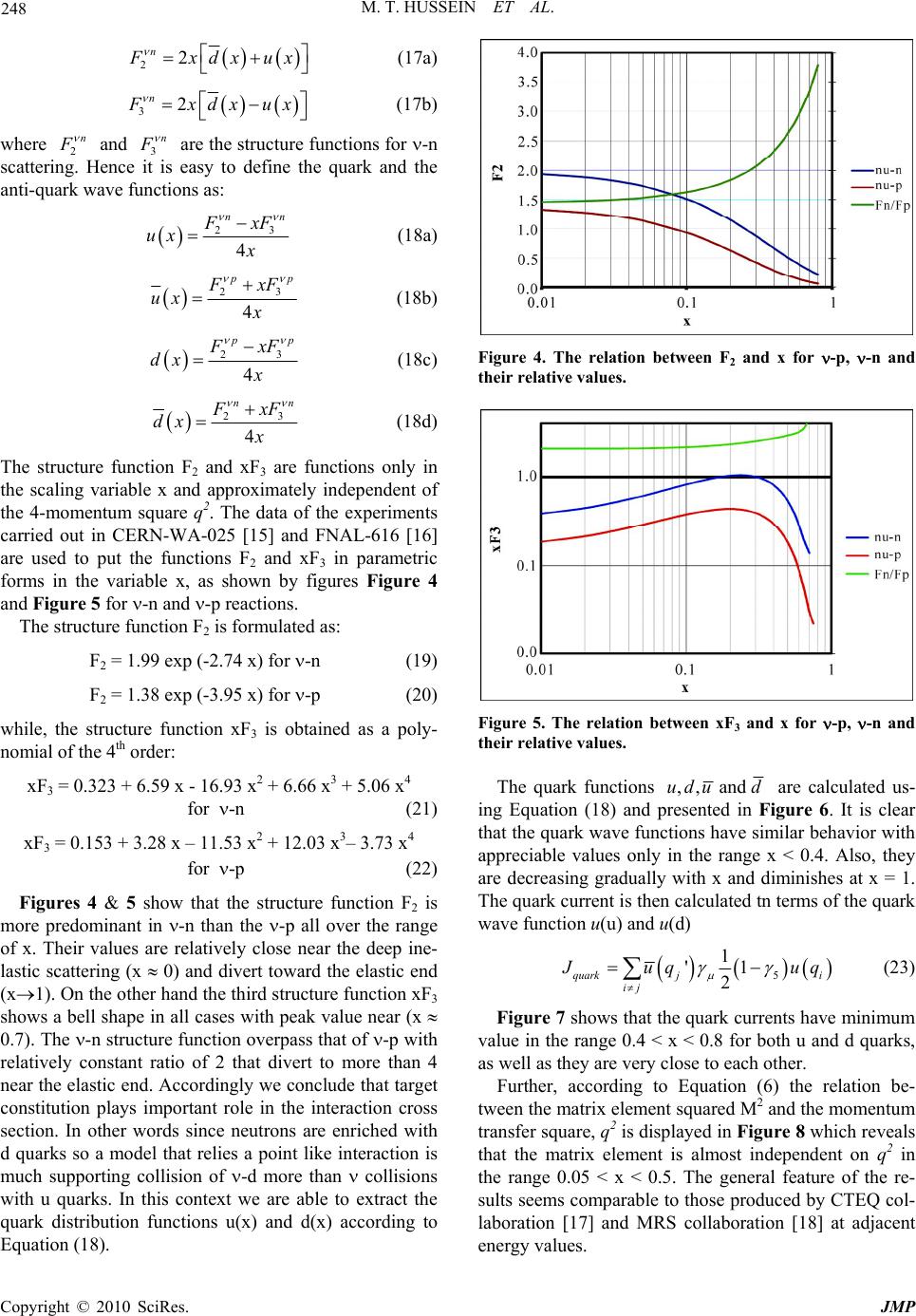

M. T. HUSSEIN ET AL.
248
 
22
n
F
xdx ux




(17a)
 
32
n
F
xdx ux




(17b)
where 2
n
F

and 3
n
F

are the structure functions for -n
scattering. Hence it is easy to define the quark and the
anti-quark wave functions as:

23
4
nn
F
xF
ux x



 (18a)

23
4
p
p
F
xF
ux x


 (18b)

23
4
p
p
F
xF
dx x


 (18c)

23
4
nn
F
xF
dx x



 (18d)
The structure function F2 and xF3 are functions only in
the scaling variable x and approximately independent of
the 4-momentum square q2. The data of the experiments
carried out in CERN-WA-025 [15] and FNAL-616 [16]
are used to put the functions F2 and xF3 in parametric
forms in the variable x, as shown by figures Figure 4
and Figure 5 for -n and -p reactions.
The structure function F2 is formulated as:
F2 = 1.99 exp (-2.74 x) for -n (19)
F2 = 1.38 exp (-3.95 x) for -p (20)
while, the structure function xF3 is obtained as a poly-
nomial of the 4th order:
xF3 = 0.323 + 6.59 x - 16.93 x2 + 6.66 x3 + 5.06 x4
for -n (21)
xF3 = 0.153 + 3.28 x – 11.53 x2 + 12.03 x3– 3.73 x4
for -p (22)
Figures 4 & 5 show that the structure function F2 is
more predominant in -n than the -p all over the range
of x. Their values are relatively close near the deep ine-
lastic scattering (x  0) and divert toward the elastic end
(x1). On the other hand the third structure function xF3
shows a bell shape in all cases with peak value near (x 
0.7). The -n structure function overpass that of -p with
relatively constant ratio of 2 that divert to more than 4
near the elastic end. Accordingly we conclude that target
constitution plays important role in the interaction cross
section. In other words since neutrons are enriched with
d quarks so a model that relies a point like interaction is
much supporting collision of -d more than  collisions
with u quarks. In this context we are able to extract the
quark distribution functions u(x) and d(x) according to
Equation (18).
Figure 4. The relation between F2 and x for -p, -n and
their relative values.
Figure 5. The relation between xF3 and x for -p, -n and
their relative values.
The quark functions ,, and udu d are calculated us-
ing Equation (18) and presented in Figure 6. It is clear
that the quark wave functions have similar behavior with
appreciable values only in the range x < 0.4. Also, they
are decreasing gradually with x and diminishes at x = 1.
The quark current is then calculated tn terms of the quark
wave function u(u) and u(d)


5
1
'1
2
quark ji
ij
J
uq uq




 (23)
Figure 7 shows that the quark currents have minimum
value in the range 0.4 < x < 0.8 for both u and d quarks,
as well as they are very close to each other.
Further, according to Equation (6) the relation be-
tween the matrix element squared M2 and the momentum
transfer square, q2 is displayed in Figure 8 which reveals
that the matrix element is almost independent on q2 in
the range 0.05 < x < 0.5. The general feature of the re-
sults seems comparable to those produced by CTEQ col-
laboration [17] and MRS collaboration [18] at adjacent
energy values.

M. T. HUSSEIN ET AL.
249
Figure 6. The wave functions of the quarks and antiquarks
u, d u and d as estimated by the empirical method.
Figure 7. The weak quark current for u and d quarks as a
function of x.
Figure 8. The matrix element squared as a function of q2 at
different x values.
5. Conclusions
In summary, neutrino-nucleon interaction was investi-
gated through intermediate vector boson (IVB). The neu-
trino wave function was derived with perturbed tech-
nique. Thus, the weak leptonic current can be obtained in
term of q2. Also, the quark wave functions were deter-
mined by empirical method based upon experimental
data and the weak hadronic current can be estimated as a
function of x.
The differential deep inelastic cross section of neu-
trino-nucleon interaction is described in terms of three
structure functions representing the three helicity states
H = 1, –1 and 0. The appreciable increase of -n cross
section compared to -p supports the point particle in-
teraction model and that  is likely dependent on the
quark flavor of the nucleon constituent quarks. The down
quark d structure function overpass that for the up quark
u at all values of x.
The quark distribution functions are also studied using
 [19], e and µ [20] inelastic scattering. The analyses are
done in the leading order (LO) and next-to-leading order
(NLO) of running coupling constant. Although the un-
certainty by the NLO perturbation show slit modification
at small x. however, they are not significant at larger x.
In both cases the result of the analysis are very close to
that obtained by the IVB model.
It is found also that the determination of the quark dis-
tribution functions are independent on the type of the
projectile of the reaction whether it is  or e.
Moreover, the total interaction matrix element is cal-
culated by IVB and NLO and found to be almost inde-
pendent on q2 in the range 0.05 < x < 0.5. The prediction
of this analysis shows global fair agreement with ex-
perimental data in the neutrino energy range (E)
150-250 GeV.
6. References
[1] J. L. Carr, arXiv: hep-ph/9903320.
[2] M. A. B. Beg and G. Feinberg, Physics Review Letters,
No. 33, 1974, p. 606.
[3] T. Siiskonen et al., Physical Review C, No. 63, 2001,
055501.
[4] J. Govaerts, Nuclear Instruments and Methods in Physics
Research Section A, No. 402, 1998, p. 303.
[5] R. P. Feynman and M. Gell-Mann, Physical Review, No.
109, 1958, p. 193.
[6] M. L. Goldberger and S. B. Treiman, Physical Review,
No. 110, 1958, p. 1178.
[7] G. Bardin et al., Physical Letters B, No. 104, 1981, p.
320.
[8] D. M. Wright et al., Physical Letters C, No. 57, 1998, p.

M. T. HUSSEIN ET AL.
250
373.
[9] T. Siiskonen et al., Physical Letters C, No. 59, 1999, p.
1839.
[10] T. Siiskonen et al, Journal of Physics G, No. 25, 1999, p.
55.
[11] B. Castel and I. S. Towner, “Modern Theories of Nuclear
Moments”, Clarendon Press, Oxford, 1990.
[12] K. Nishikawa, Conference of High Energy Physics Hep
2001, Budapest 2001, Invited talk.
[13] S. M. Bilenky, arXiv: hep-ph/0103091.
[14] D. H. Perkins, International Europhysics Conference HEP2001,
Budapest 2001, Invited talk.
[15] A. G. Tenner and N. N. Nikolaev, Nuovo Cimento A, No.
105, 1992, p. 1001.
[16] R. Blair et al., Physical Review Letters, No. 51, 1983, p.
343.
[17] H. L. Lai et al., Physical Review D, No. 51, 1995, p.
4763.
[18] A. D. Martin et al., Physical Review D, No. 47, 1993, p.
867.
[19] A. Bodek and U. K. Yang, Nuclear Physics B, No. 112,
2002, p. 70.
[20] J. F. Owens et al., Physical Review D, No. 75, 2007, p.
054030.