J. Mod. Phys., 2010, 1, 217-225
doi:10.4236/jmp.2010.14033 Published Online October 2010 (http://www.SciRP.org/journal/jmp)
Nuclear Model Calculations on the Production of Auger
Emitter 165Er for Targeted Radionuclide Therapy
Mahdi Sadeghi1, Milad Enferadi2, Claudio Tenreiro 3
1Agricultural, Medical and Industrial Resear ch Sch o ol , Nuclear Science and Technology
Research Institute, Karaj, Iran
2Faculty of Engineering, Researc h an d Sci ence Campus, Islamic Azad University, Tehran, Iran
3
Department of Energy Science Sungkyunkwan University, Suwon, Korea
Received June 6, 2010; revised July 16, 2010; accepted June 25, 2010
Abstract
Auger electron emitting radionuclides have potential for the therapy of small-size cancers because of their
high level of cytotoxicity, low-energy, high linear energy transfer, and short range biologic effectiveness.
Auger emitter 165Er (T1/2 = 10.3 h, IEC = 100%) is a potent nuclide for targeted radionuclide therapy. 165Er ex-
citation function via 165Ho(p,n)165Er, 165Ho(d,2n)165Er, 166 Er(p,2n)165Tm→165Er, 166Er(d,3n)165Tm→165Er,
natEr(p,xn)165Tm→165Er and 164Er(d,n)165Tm→165Er reactions were calculated by ALICE/91, ALICE/ASH
(GDH Model & Hybrid Model) and TALYS-1.2 (Equilibrium & Pre-Equilibrium) codes and compared to
existing data. Requisite for optimal thicknesses of targets were obtained by SRIM code for each reaction.
Keywords: 165Er, Auger Electron, Excitation Functions, TALYS-1.2, ALICE-ASH
1. Introduction
The double strand DNA helix presents a diameter of 2
nm. In a typical Auger radiation decay, the highest en-
ergy deposition occurs in spheres of 1-2 nm, as described
elsewhere [1]. This means that the calculated local en-
ergy deposition of an Auger emitter incorporated into
DNA would hit both DNA strands with an energy of 1.6
MGy or higher. This radiation energy is therefore largely
sufficient to disrupt both DNA strands over distances of
several nucleotides [2,3]. Auger electron emitting ra-
dionuclides in cancer therapy offer the opportunity to
deliver a high radiation dose to the tumor cells with high
radiotoxicity while minimizing toxicity to normal tissue
[4]. Besides the direct effect of Auger electrons on DNA
double strands, an indirect radiation effect of Auger en-
ergy deposition will occur via production of radicals [5].
The radicals diffuse freely in the intracellular space and
can cause further DNA damage. Even a bystander effect
by diffusion of radicals through gap junctions has been
described [6]. Only very few radionuclides exists that
decay exclusively by EC-mode without any accompany-
ing radiation, 165Er is one of them. Auger electrons are
emitted by isotopes that decay by electron capture (EC)
or have internal conversion (IC) in their decay. In each
decay of these isotopes, a cascade of very low energy
electrons is emitted [7].
In this work, several methods for 165Er production us-
ing ALICE/91, ALICE/ASH (GDH Model & Hybrid
Model) and TALYS-1.2 (Equilibrium & Pre-Equilibrium)
codes have been studied. Aim of the presented study is to
compare the calculated cross sections for the production
of 165Er via different reactions with incident particle en-
ergy up to 50 MeV as a part of systematic studies on
particle-induced activations on metal targets, theoretical
calculation of production yield, calculation of target
thickness requirement and suggestion for optimum reac-
tion to produce Erbium-165.
2. Theory
2.1. Calculation of Excitation Function
Cross sections for 165Ho + p,d 166Er + p,d 164Er + d and
natEr + p reactions were calculated by using ALICE/91,
ALICE/ASH (GDH Model & Hybrid Model) and TA-
LYS-1.2 (Equilibrium & Pre-Equilibrium) codes [9-11].
The codes were used simultaneously to increase the ac-
curacy of calculations. An optimum energy range was
determined and employed to avoid the formation of the
radionuclide impurities and decrease the excitation func-
tions of the inactive impurities as far as possible. To fur-

M. SADEGHI ET AL.
218
ther achieve the aim, feasibility of the 165Er production
via various nuclear reactions per low/medium energy
accelerators was investigated. According to SRIM code
(The Stopping and Range of Ions in Matter); the required
thickness of the target was calculated for each reaction.
2.2. ALICE/ASH Code
The ALICE/ASH code [12] is a modified and advanced
version of the ALICE code [9] and ALICE/LIVERMORE.
The geometry dependent hybrid model (GDH) as
adopted originally is used for the description of the
pre-equilibrium particle emission from nuclei [13,14].
2.2.1. Pre-Compound Deuteron Emission
Following closely the exhaustive analysis of the code
ALICE/ASH by Broeders and its collaborators [12] the
main features of the deuteron emission from the com-
pound systems (as a cluster), relative to the Fermi En-
ergy (EF), from all the reaction channels, are summarized
as:
1) At energies below the EF, the pick-up of nucleons,
2) At energies above EF the possible coalescence of
states of two excited nucleons,
3) The possibility of reactions that includes the
Knock-out of a “pre-formed” deuteron
4) Finally the inclusion of a fast or peripheral direct
mechanism resulting in deuteron formation and escape.
Taking into consideration all the above, the modified
code calculates the deuteron spectrum from the contribu-
tion of the individual differential cross sections of such
processes as
PU,C KO D
dd dd
ddd d
dεdεdεdε


 (1)
The upper index stands for Pick-Up, Coalescence,
Knock-out and Direct reaction respectively. The cross
sections are in somehow proportional to the relative
number of states available for such reaction channel to
occur. Expressions for such cross sections were derived
by Broeders et al. [13].
Using basic statements of the hybrid model [15]. The
exciton level density is calculated by Beták and Dobeš
[23] taking into account the finite depth of the nuclear
potential well
 


n1
hkF
ph
hk F
k0
Ek E
ωp,h,Eg gC1EkE
p
!h!n1 !





 (2)
where E is the excitation energy, EF is the Fermi energy,
g and g
 are the single particle level densities for parti-
cles and holes, respectively, Θ(x) is the Heaviside func-
tion, Θ = 0 for x < 0 and Θ = 1 for x > 0.The single par-
ticle level densities for particles and holes are calculated
by Beták and Dobeš [16]
g = A/14 (3)
F
gA/E

 (4)
One should note that nuclear surface effects [17-19]
influence the effective value of the Fermi energy EF used
for the calculation of pre-compound particle spectra.
This point is discussed below. The exciton coalescence
pick-up model proposed by Sato et al. [20] is used for the
calculation of the dσ P-U,C/dεd spectrum component [28].
 





 
0
e
PU,C
dd
non0k,mddd n
e
nn km2
ddd dd
λε ωp-k,h,U
dσσEεQgD
dεωp,h,E λε λε
F





 (5)
where Fk,m is the deuteron formation factor equal to the
probability that the deuteron is composed of “k” particles
above the Fermi level and “m” particles below; εd is the
channel emission energy corresponding to the deuteron
emission; λe
d is the deuteron emission rate; λ+ d is the in-
tranuclear transition rate for the absorption of the deu-
teron in the nucleus; gd is the density of single particle
states for the deuteron. The deuteron emission (λe
d) and
absorption (λ+
d) rates are calculated. In analogy with
α-particle emission the knock-out component of the
pre-compound deuteron emission spectrum is written as
follows
 





 

0
e
kO
dd
non 0d 0d
e
nn
dd dd dd
λε
ωp-1,h,U
dσg
σEΦEgDn
dεgp ωp,h,Eλε λε




 (6)
where the factor Φd describes the initial number of ex-
cited deuteron clusters in the nucleus
Φd = 2Fd (E0) (7)
where Fd is the probability of interaction of the incident
particle with the “pre-formed” deuteron resulting in its
excitation in the nucleus; and the factor of two reflects
the normalization on the number of particles in the initial
exciton state n0. The general expression for Fd is [21]

M. SADEGHI ET AL.
219




 
xd 0
d
xp 0xn 0xd 0
σE
FAZ
ZσEσEσE
AA



 

(8)
where “x” refers to the initial proton or neutron, σxd, σxp
and σxn are the cross-sections of the elastic interaction of
projectile with deuteron, proton and neutron, respectively,
corrected for a Pauli principle,

is the number of
“pre-formed” deuterons in the nucleus, Z’ and A’ are the
number of protons and nucleons in the nucleus corrected
for a number of clustered deuterons.
The direct component of the deuteron spectrum is [21]



 
e *
dd
non d
e
ddd dd
λε ωU
dσσg
dεω1p,0h,E λε λε
D

 (9)
where the final level density ω*(U) is approximated by
ω(0p,1h,U).γ/gd with the γ value equal to 0.002 MeV−1
for all nuclei and excitation energies. To improve the
agreement of calculations and the measured deuteron
spectra, it is useful to write the direct component of the
spectrum in the following form

 
e
2 D
dd
2F
non 1d
2e +
d3Fdddd
λε
(E α E) dσ=σαexp g
dε2(αE) λε+λε





(10)
where α1, α2 and α3 are parameters and EF is the effective
value of the Fermi energy. The values of αi can be ob-
tained from analysis of experimental deuteron spectra.
The global parameterization of αi parameters is hardly
possible [12].
2.3. TALYS-1.2 Code
TALYS-1.2 code is optimized for incident projectile
energies, ranging from 1 keV up to 200 MeV on target
nuclei with mass numbers between 12 and 339. It in-
cludes photon, neutron, proton, deuteron, triton, 3He, and
α-particles as both projectiles and ejectiles, and sin-
gle-particle as well as multi-particle emissions and fis-
sion. All experimental information on nuclear masses,
deformation, and low-lying states spectra is considered,
whenever available [22] and if not, various local and
global input models have been incorporated to represent
the nuclear structure properties, optical potentials, level
densities, γ-ray strengths, and fission properties. The
TALYS code was designed to calculate total and partial
cross sections, residual and isomer production cross sec-
tions, discrete and continuum γ-ray production cross sec-
tions, energy spectra, angular distributions, double dif-
ferential spectra, as well as recoil cross sections. The
pre-equilibrium particle emission is described using the
two-component Exciton model. The model implements
new expressions for internal transition rates and new
parameterization of the average squared matrix element
for the residual interaction obtained using the optical
model potential [23,24]. The phenomenological model is
used for the description of the pre-equilibrium complex
particle emission. The equilibrium particle emission is
described using the Hauser-Feshbach formalism.
3. Results
In the calculations of the hybrid and GDH model, the
code ALICE/ASH was used. This code can be applied
for the calculation of excitation functions, energy and
angular distribution of secondary particles in nuclear
reactions induced by nucleons and nuclei with energy
up to 300 MeV. The generalized superfluid [25] has
been applied for nuclear level density calculations in the
ALICE/ASH code. The ALICE-91 and ALICE/ASH
codes use the initial exciton number as n0 = 3. But in
these models the different alpha (α), deuteron (d) and
proton (p) exciton numbers are used in the pre-equilib-
rium GDH model calculations. In details, the other code
model parameters can be found in reference [12]. In
ALICE/ASH code, the hybrid and geometry dependent
hybrid model (GDH) for pre-compound emissions and
the Weisskopf-Ewing model for compound reactions are
selected.
Although there are some discrepancies between the
calculations and the experimental data, in generally, the
new evaluated hybrid and GDH the pre-equilibrium
model calculations (with ALICE/ASH) are very close to
the experimental data in Figures 1, 2, and 6. In addition,
the GDH and hybrid model calculations are close to each
other, generally. Indeed, calculated emission cross sec-
tions with GDH and hybrid model by using ALICE/ASH
code show the best agreement with the experimental data
for natEr(p,xn)165Tm→165Er reaction in Figure 6. More-
over, these cross sections in harmony with the experi-
mental data for 165Ho(p,2n)165Er nuclei except for the
(p,n) reaction in which the experimental data have fol-
lowed above theoretical calculations in Figure 1.
The reason is that the new developed pre-equilibrium
reaction mechanism ALICE/ASH includes angular mo-
mentum conversion. Not only it gives us more informa-
tion for new nuclear reaction research, but also it lets us
calculate cross sections up to many hundreds MeV en-
ergy level. In fact, when taking the pairing energy and
the mass shell correction into consideration, the experi-
mental values are in better agreement with the theoretical
results [26]. In conclusion all figures show that, although
a few calculated data follow the experimental ones from
above or below as parallel, generally all the compared
data are in agreement with each other.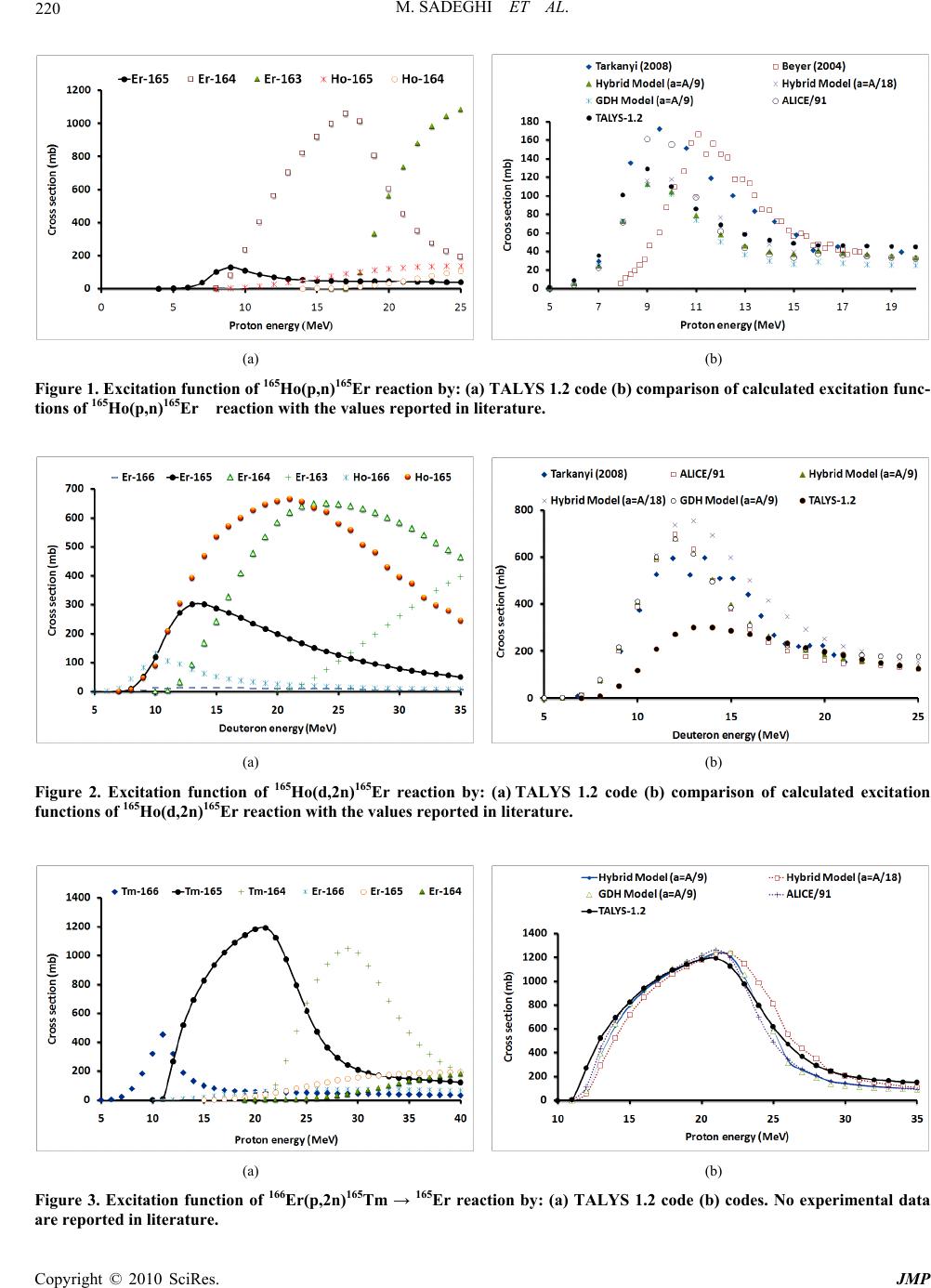

M. SADEGHI ET AL.
220
(a) (b)
Figure 1. Excitation function of 165Ho(p,n)165Er reaction by: (a) TALYS 1.2 code (b) comparison of calculated excitation func-
tions of 165Ho(p,n)165Er reaction with the values reported in literature.
(a) (b)
Figure 2. Excitation function of 165Ho(d,2n)165Er reaction by: (a) TALYS 1.2 code (b) comparison of calculated excitation
functions of 165Ho(d,2n)165Er reaction with the values reported in literature.
(a) (b)
Figure 3. Excitation function of 166Er(p,2n)165Tm → 165Er reaction by: (a) TALYS 1.2 code (b) codes. No experimental data
are reported in literature.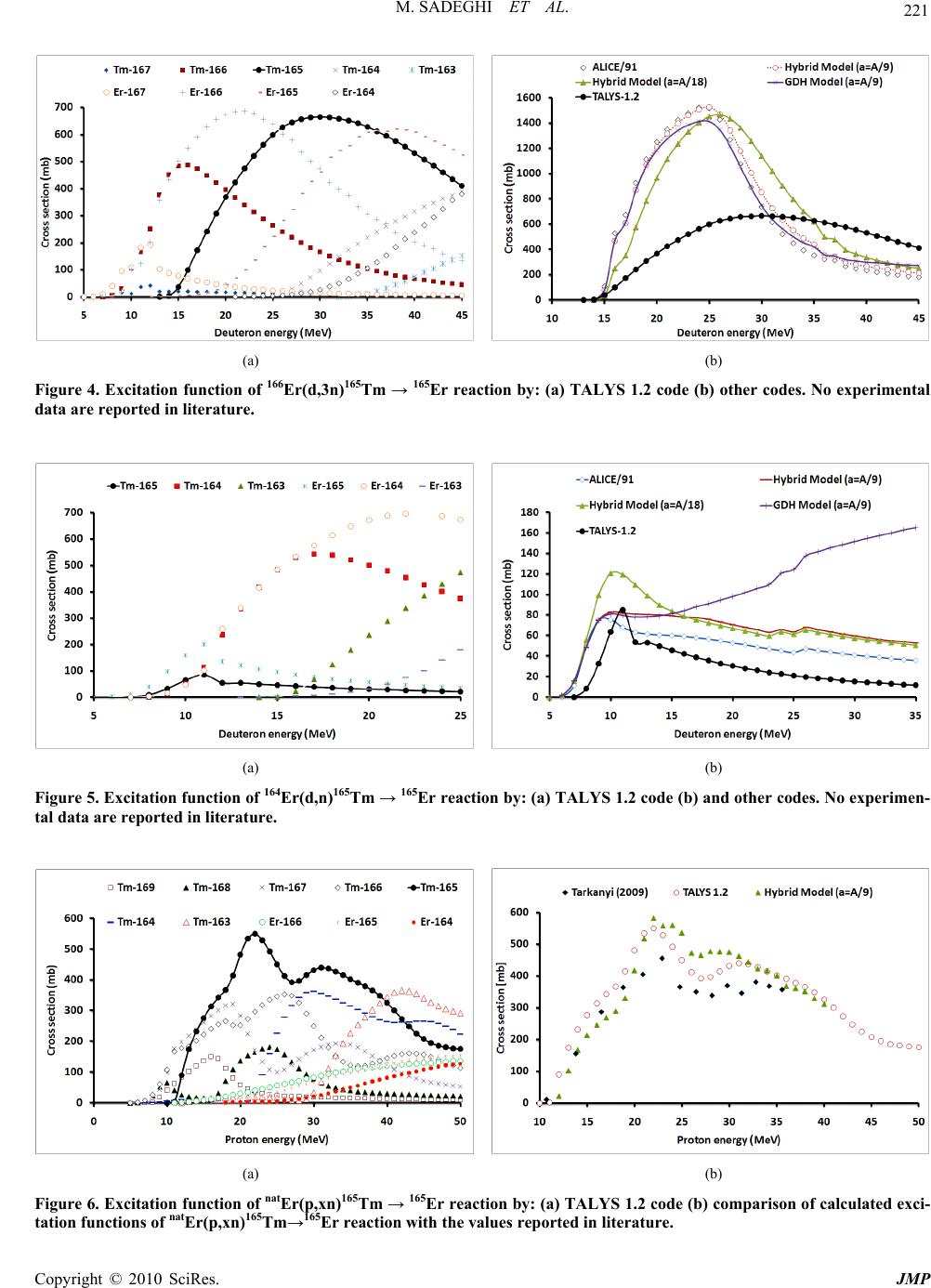

M. SADEGHI ET AL.
221
(a) (b)
Figure 4. Excitation function of 166Er(d,3n)165Tm → 165Er reaction by: (a) TALYS 1.2 code (b) other codes. No experimental
data are reported in literature.
(a) (b)
Figure 5. Excitation function of 164Er(d,n)165Tm → 165Er reaction by: (a) TALYS 1.2 code (b) and other codes. No experimen-
tal data are reported in literature.
(a) (b)
Figure 6. Excitation function of natEr(p,xn)165Tm → 165Er reaction by: (a) TALYS 1.2 code (b) comparison of calculated exci-
tation functions of natEr(p,xn) 165Tm→165Er reaction with the values reported in literature.

M. SADEGHI ET AL.
222
3.1. Excitation Function of 165Ho(p,n) 165Er
Reaction
Excitation functions of the proton-induced reaction on
Holmium-165 were determined by ALICE/91, AL-
ICE/ASH and TALYS-1.2 codes, and the experimental
data that have been studied by Beyer et al. (2004) [27]
and Tárkányi et al. (2008) [28]. The evaluation of the
results of the calculations showed that the best range of
energy that favor the reaction is from 12 to 7 MeV. Car-
rier-free 165Er production can be obtained using a proton
an energy of less than 9 MeV. There is a relatively good
agreement between the experimental data by Tárkányi et
al. and the prediction of the excitation function made by
ALICE/91 code up to 11 MeV. According to calculations
from SRIM code the required target thickness should be
34.04 µm (See Figure 1).
3.2. Excitation Function of 165Ho(d,2n) 165Er Re-
action
According to results from the ALICE/91, ALICE/ASH
and TALYS-1.2 codes, the optimum energy range for the
projectile particle (deuteron) to produce 165Er from 165Ho
target in this case is from 16 to 11 MeV. Hybrid Model
predicts that the maximum of the cross section (a = A/18)
is 753.6 mb at an energy of 13 MeV. The separation of
isotope impurities is not possible by chemical methods,
so this reaction is non carrier free for 165Er production
(See Figure 2). This reaction was investigated only by
Tárkányi et al. (2008) [29]. ALICE/91 and ALICE/ASH
codes agree well with the measured data from Tárkányi
et al. up to 20 MeV. Also, the results of TALYS-1.2
code are less than experimental data, ALICE/91 and
ALICE/ASH codes.
3.3. Excitation Function of
166Er(p,2n)165Tm→165Er Reaction
165Er can also be produced using the 166Er(p,2n)165Tm
reaction which is unstable, 165Tm (T1/2 = 30.06 h), the
best range of incident energy was estimated for proton
energies from 23 to 16 MeV. The maximum for the cross
section, as by the GDH model (a = A/9) is predicted to
be 1263.3 mb at the energy of 21 MeV. Also 166/164Tm
impurities are generated which cannot be separated by
chemical methods. Also this reaction was leading to
non-isotopic impurities of stable (166/164Er). There have
not been any experimental data for these reactions in the
literature, therefore only theoretical calculations have
been shown in Figure 3. Also, there is a relatively good
agreement between the prediction of the excitation func-
tion made by TALYS-1.2, ALICE/91 and ALICE/ASH
codes. The theoretical thick target will give a yield of
107.3 MBq/µA·h. Recommended thickness of the target
is 31.8 µm.
3.4. Excitation Function of
166Er(d,3n)165Tm→165Er Reaction
According to codes, optimal energy range of the projec-
tile particle (deuteron) to produce 165Tm from 166Er target
is from 22 to 29 MeV within this range the maximum
cross section predicted by Hybrid Model (a = A/9) is
1523.9 mb at an energy of 25 MeV. Also 166Tm (T1/2 =
7.7 h), 164Tm (T1/2= 2 min) and 163Tm (T1/2 = 1.81 h) im-
purities are generated which cannot be separated by
chemical methods. The non-isotopic impurities of active
(166/165Er) were also produced in the reaction. There have
not been any experimental data for these reactions in the
literature, therefore only theoretical calculations have
been shown in Figure 4, so nuclear model calculations
can play an important role in excitation function of
166Er(d,3n)165Tm→165Er reaction. Also, the results of
TALYS-1.2 code are less than ALICE/91 and AL-
ICE/ASH codes. The theoretical thick target gives a yield
of 42.9 MBq/µAh. Recommended thickness of the target
is 31.4 µm.
3.5. Excitation Function of
164Er(d,n)165Tm→165Er Reaction
According to ALICE/91, ALICE/ASH and TALYS-1.2
codes, the best energy range of the projectile particle
(Deuteron) to produce 165Tm from 164Er target is found to
be from 13 to 8 MeV and maximum cross section is pre-
dicted by the Hybrid model(a = A/18) to be 120.4 mb at
an energy of 10 MeV. Also 164Tm (T1/2 = 2 min) and
163Tm (T1/2 = 1.81 h) impurities are generated and they
could not be separated by chemical methods (See Figure
5). This reaction was also producing Non-isotopic impu-
rities of high cross section (164/163Er). The theoretical
thick target yield is 0.074 MBq/µA·h. Recommended
thickness of the target is 90 µm.
3.6. Excitation Function of
natEr(p,xn)165Tm→165Er Reaction
Excitation functions of the proton-induced reaction on
natEr were calculated by ALICE/ASH and TALYS-1.2
codes. The data from the calculations showed that in
order to optimize isotope production the best range of the
energy is 29 to 20 MeV. The calculated excitation func-
tions of natEr(p,xn)165Tm→165Er reactions are compared
with the existing experimental values in Figure 6. The
results of TALYS-1.2 and ALICE/ASH codes are good

M. SADEGHI ET AL.
223
Table 1. 165Er production yield via different nuclear reactions by SRIM and TALYS 1.2 codes.
Reaction Isotopic abundance
(%)
Energy range
(MeV)
Target thickness
(m)
Theorical yield
(MBq/Ah)
165Ho(p,n) 165Er 100 12→7 75 34.04
165Ho(d,2n)165Er 100 16→11 61 77.7
166Er(p,2n)165Tm→165Er 33.6 23→16 31.8 107.3
166Er(d,3n)165Tm→165Er 33.6 29→22 31.4 42.9
164Er(d,n)165Tm→165Er 1.61 13→8 90 0.074
natEr(p,xn )165Tm→165Er 100 29→20 27.9 210.9
agreement with the measured data from Tárkányi et al.
(2009) [30]. The separation of isotope impurities is not
possible by chemical methods, so this reaction is non
carrier free for 165Tm production. According to SRIM
code the required target thickness should be 210.9 µm.
3.7. Calculation of the Required Thickness of
Target
To obtain the optimum physical dimensions of the target
such as the thickness some estimations from the SRIM
code (The Stopping and Range of Ions in Matter); were
performed [31]. The physical thickness of the target layer
is chosen in such a way that, for a given beam/target an-
gle geometry (90°), the incident beam on the target area
will produce a compound nucleus with an excitation en-
ergy with the calculated optimum energy to favor the
selected evaporation channel. To minimize the thickness
of the thin film target, a geometry of 6° is preferred; so
the required thickness of the layer will be smaller with a
coefficient 0.1 (note: it is not clear what this phrase
means, what is such coefficient). The calculated thick-
nesses for these ideal reactions are shown in Table 1.
3.8. Calculation of Theoretical Yield
Enhance of the projectile energy, the beam current and
the time of bombardment increase the production yield.
The production yield can be calculated as below,

 
-1
E2
-λt L
E1
NH dE
Y=I 1eσEdE
Mdρx




 (11)
where Y is the product activity (in Bq) of the product, NL
is the Avogadro number, H is the isotope abundance of
the target nuclide, M is the mass number of the target
element, σ(E) is the cross section at energy E, I is the
projectile current, dE d( x)

is the stopping power, λ is
the decay constant of the product and t is the time of ir-
radiation [32]. The production yields of 165Er via differ-
ent reactions were calculated using the Simpson numeri-
cal integral as of Equation (11) (Table 1).
4. Conclusions
Result of the calculations and considerations predicted
that the high yield will be achieved by deuteron bom-
bardment of a natural erbium target. Nevertheless this
processes lead to form the radioisotope and isotope im-
purities that have high cross section than 165Er. 164Er
(d,n)165Tm→165Er, 166Er(d,3n)165Tm→165Er and 165Ho
(d,2n)165Er reactions are too much undesirable than the
prior reaction, Because of high impurities go along with
the product. However, 165Er production via 166Er(p,2n) 165
Tm→165Er reaction lead to high cross section for 165Tm,
but this reaction can not be resulted in no-carrier added
of 165Er production. 165Ho(p,n ) 165Er is suggested as the
best method to produce 165Er, generating minimum im-
purities. Moreover, its non-carrier added production fea-
sibility using proton energy of less 9 MeV can be con-
sidered as a brilliant advantage. Solvent extraction (by
HDEHP (di-(2-ethylhexyl) phosphoric acid); H3Cit (cit-
ric acid); HLact (lactic acid) and HGlyc (glycolic acid)
and ion exchange chromatography are the best method
which used for separation erbium radionuclides from Ho
targets solution.
5. References
[1] A. I. Kassis, “Cancer Therapy with Auger Electrons: Are
We Almost There?” Journal of Nuclear Medicine, Vol.
44, No. 9, 2003, pp.1479-1481.
[2] J. L. Humm, R. W. Howell and D. V. Rao, “Dosimetry of
Auger-Electron-Emitting Radionuclides, Report No. 3 of
AAPM Nuclear Medicine, Task Group No. 6,” Medical
Physics, Vol. 21, No. 12, 1994, pp. 1901-1915.
[3] R. W. Howell, V. R. Narra, K. S. Sastry and D. V. Rao,

M. SADEGHI ET AL.
224
“Auger Electron Dosimetry, Report No. 37 of AAPM
Nuclear Medicine, Task Group No. 2,” Medical Physics,
Vol. 19, No. 16, 1992, pp. 1352-1383.
[4] H. Thisgaard, “Accelerator Based Production of Au-
ger-Electron Emitting Isotopes for Radionuclide Ther-
apy,” Denmark, Risø-PhD-42(EN), 2008, pp. 2-6.
[5] A. Bishayee, D. V. Rao and R. W. Howell, “Radiation
Protection by Cysteamine Against the Lethal Effects of
Intracellularly Localized Auger Electron, α-, and β-Par-
ticle Emitting Radionuclides,” Acta Oncology, Vol. 39,
No. 6, 2000, pp. 713-717.
[6] A. Bishayee, H. Z. Hill, D. Stein, D. V. Rao and R. W.
Howell, “Free Radical-Initiated and Gap Junction- Medi-
ated Bystander Effect Due to Non-Uniform Distribution
of Incorporated Radioactivity in a Three-Dimensional
Tissue Culture Model,” Radiation Research, Vol. 155,
No. 2, 2001, pp. 335-344.
[7] A. Kassis and S. J. Adelstein, “Radiobiologic Principles
in Radionuclide Therapy,” Nuclear Medicine, Vol. 46,
No. 1, 2005, pp. 4S-12S.
[8] A. Kassis, “Therapeutic Radionuclides: Biophysical and
Radiobiologic Principles,” Seminars in Nuclear Medicine,
Vol. 38, No. 5, 2008, pp. 358-366.
[9] M. Blann, “ALICE-91, Statistical Model Code System
with Fission Competition, RSIC Code,” PACKAGE PSR
-146, 1991.
[10] A. Yu. Konobeyev, Yu. A. Korovin and P. E. Pereslavtsev,
“Code ALICE/ASH for Calculation of Excitation Func-
tions, Energy and Angular Distributions of Emitted Parti-
cles in Nuclear Reactions,” Report of the Obninsk Insti-
tute of Nuclear Power Engineering, 1997.
[11] Yu. A. Korovin, A. Yu. Konobeyev, P. E. Pereslavtsev, C.
Broeders, I. Broeders, U. Fischerr and U. von Möllen-
dorff, “Evaluated Nuclear Data Files for Accelerator
Driven Systems and Other Intermediate and High-Energy
Applications,” Nuclear Instruments and Methods in
Physics Research, Section A, Vol. 463, No. 3, 2001, pp.
544-556.
[12] C. H. M. Broeders, A. Yu. Konobeyev and Yu. A.
Korovin, “ALICE/ASH–Pre-Compound and Evaporation
Model Code System for Calculation of Excitation Func-
tions, Energy and Angular Distributions of Emitted Parti-
cles in Nuclear Reactions at Intermediate Energies,” For-
schungszentrum Karlsruhe GmbH, Karlsruhe, Report FZKA
2006.
http://bibliothek.fzk.de/zb/berichte/FZKA7183.pdf
[13] C. H. M. Broeders and A. Yu. Konobeyev, “Phenome-
nological Model for Non-Equilibrium Deuteron Emission
in Nucleon Induced Reaction,” Kerntechnik, Vol. 70, No.
5-6, 2005, pp. 260-269.
[14] A. Iwamoto and K. Harada, “Mechanism of Cluster
Emission in Nucleon,” Physical Review C-Nuclear Phys-
ics, Vol. 26, No. 5, 1982, pp. 1821-1834.
[15] M, Blann, “Hybrid Model for Pre-equilibrium Decay in
Nuclear Reactions,” Physical Review Letters, Vol. 27, No.
6, 1971, pp. 337-340.
[16] E. Beták and J. Dobeš, “The Finite Depth of the Nuclear
Potential Well in the Exciton Model of Preequilibrium
Decay,” Zeitschrift für Physik A: Atoms and Nuclei, Vol.
279, No. 3, 1976, pp. 319-324.
[17] C. Kalbach, “Surface and Collective Effects in Preequi-
librium Reactions,” Physical Review C-Nuclear Physics,
Vol. 62, No. 4, 2000, pp. 446081-4460814.
[18] C. Kalbach, “Erratum: Surface and Collective Effects in
Preequilibrium Reactions,” Physical Review C-Nuclear
Physics, Vol. 64, No. 3, 2001, p. 39901(E).
[19] C. Kalbach, “Surface Effects in Pre-equilibrium Reac-
tions of Incident Neutrons,” Physical Review C-Nuclear
Physics, Vol. 69, No. 1, 2004, p. 14605.
[20] K. Sato, A. Iwamoto and K. Harada, “Pre-equilibrium
Emission of Light Composite Particles in the Framework
of the Exciton Model,” Physical Review C, Vol. 28, No. 4,
1983, pp. 1527-1537.
[21] A. Yu. Konobeyev and Yu. A. Korovin, “Calculation of
Deuteron Spectra for Nucleon Induced Reactions on the
Basis of the Hybrid Exciton Model Taking into Account
Direct Processes,” Kerntechnik, Vol. 61, No. 1, 1996, pp.
45-49.
[22] T. Belgya, O. Bersillon, T. Fukahori et al., “Handbook
for Calculations of Nuclear Reaction Data,” IAEA-TEC-
DOC-1506, Vienna, Austria, 2006.
[23] A. J. Koning, S. Hilaire and M. Duijvestijn, “TALYS-1.2
A Nuclear Reaction Program, User Manual,” NRG, Nether-
lands, 2009, pp. 16-18.
[24] V. F. Weisskopf and D. H. Ewing, “Excitation of Nuclei
by Bombardment with Charged Particles,” Physical Re-
view, Vol. 57, No. 12, 1940, pp. 472-485.
[25] A. V. Ignatyuk, K. K. Istekov and G. N. Smirenkin, “The
Role of Collective Effects in the Systematics of Nuclear
Level Densities,” Yadernaya Fizika, Vol. 29, No. 4, 1979,
pp. 875-883.
[26] H. Büyükuslu, A. Kaplan, E. Tel, A. Aydin, G. Yıldırım
and M. H. Bölükdemir, “Theoretical Cross Sections of
209Bi, 232Th, 235U and 238U on Deuteron-Induced Reac-
tions,” Annals of Nuclear Energy, Vol. 37, No. 4, 2010,
pp. 534- 539.
[27] G. J. Beyer, S. K. Zeisler and D. W. Becker, “The Au-
ger-electron Emitter Er-165: Excitation Function of the
Ho-165(p,n)Er-165 Process,” Radiochimica Acta, Vol. 92,
No. 4-6, 2004, pp. 219-223.
[28] F. Tárkányi, A. Hermanne, S. Takacs, F. Ditrói, B. Király
et al., “Experimental Study of the 165Ho(p,n) Nuclear
Reaction for Production of the Therapeutic Radioisotope
165Er,” Nuclear Instruments and Methods in Physics Re-
search, S ect ion B, Vol. 266, No. 15, 2008, pp. 3346-3352.
[29] F. Tárkányi, F. S. Takacs, A. Hermanne, F. Ditrói, “Ex-
perimental Study of the 165Ho(d,2n) and 165Ho(d,p) Nu-
clear Reactions up to 20 MeV for Production of the
Therapeutic Radioisotopes 165Er and 166gHo,” Nuclear In-
struments and Methods in Physics Research, Section B,
Vol. 266, No. 16, 2008, pp. 3529-3534.
[30] F. Tárkányi, F. S. Takacs, A. Hermanne, F. Ditrói et al.,
“Investigation of Production of the Therapeutic Radio-
isotope 165Er by Proton Induced Reactions on Erbium in

M. SADEGHI ET AL.
225
Comparison with Other Production Routes,” Applied Ra-
diation and Isotope, Vol. 67, No. 2, 2009, pp. 243-247.
[31] J. Ziegler, J. Biersack and U. Littmark, “The Stopping
and Range of Ions in Matter, SRIM Code,” USA, 2006.
http://www.srim.org/
[32] M. Sadeghi, A. Zali and B. Zeinali, “86Y Production via
86Sr(p,n) for PET Imaging at a Cyclotron,” Applied Ra-
diation and Isotope, Vol. 67, No. 7-8, 2009, pp. 1393
-1396.