J. Mod. Phys., 2010, 1, 211-216
doi:10.4236/jmp.2010.14032 Published Online October 2010 (http://www.SciRP.org/journal/jmp)
Dielectric and Mechanical Nonlinear Behavior of Mn
Doped PMN-35PT Ceramics
Diouma Kobor1, Abdelowahed Hajjaji2, Jose E. Garcia3, Rafel Perez3, Alfons Albareda3,
Laurent Lebrun4, Daniel Guyomar4
1Laboratoire de Chimie et Physique des Matériaux (LCPM), Université de Ziguinchor, Quartier Diabir,
Ziguinchor, Sénégal
2Ecole Nationale des Sciences Appliquées d’El Jadida, EL Jadida, Morocco
3Departament de Fisica Aplicada, Universitat Politècnica de Catalunya, Jordi Girona 1-3, Campus Nord,
Barcelona, Spain
4INSA, LGEF, Bat Gustave FERRIE, 8 Rue de la Physique, Villeurbanne Cedex, France
Received August 14, 2010; revised September 26, 2010; accepted August 30, 2010
Abstract
This paper presents an investigation on dielectric and mechanical nonlinear properties in Mn-doped
PMN-35PT ceramics. The structural study of the ceramics verifies that the 1% mol Mn doped PMN-35PT is
a pure perovskite phase with a tetragonal symmetry. SEM micrograph shows the same microstructural mor-
phology of an undoped ceramic. From the EPR spectra, it has been concluded that the major part of Mn is
present in Mn2+ rather than in Mn4+ form. The addition of Mn2+ ions acts on the dielectric, piezoelectric and
mechanical properties by decreasing the relative dielectric permittivity (3800 to 2074), the dielectric losses
(0.60 to 0.53), the piezoelectric coefficient d33 (650 to 403 pC/N), and increasing the mechanical quality fac-
tor Qm (78 to 317). It was found that in Mn2+ doped ceramics the dielectric response can not be described by
Rayleigh law. This result can be understood taking into account that reversible motion of the domain wall is
a relevant contribution to response of this material.
Keywords: Piezoelectrics, Ceramics, Nonlinearity, Dielectric properties, Mechanical Properties, PMN-PT
1. Introduction
Since the discovery of relaxor behavior in Pb(Mg1/3Nb2/3)O3
(PMN) system by Smolenskii and Agranovskaya [1],
many investigations on mixed B-site cation relaxor
ferroelectrics, i.e. Pb(BI1/3BII2/3)O3-type perovskites,
have been performed due to their excellent dielectric and
electromechanical properties [2]. Lead magnesium nio-
bate-lead titanate (1 − x) [Pb (Mg1/3Nb2/3) O3]-xPbTiO3
(PMN-PT) is a solid solution of relaxor PMN and nor-
mal PbTiO3 (PT) ferroelectrics which represent a typical
example of such perovskites. These materials with com-
position close to the morphotropic phase boundary (MPB)
exhibit unusually high electromechanical coupling coef-
ficients and electrically induced strain [3]. The investiga-
tion of compositions near the MPB region has attracted
particular attention owing to their excellent piezoelectric
and dielectric properties, which make them promising
candidate materials for applications in multilayer ce-
ramic capacitors, as well as ceramic electrostrictive ac-
tuators and field-induced electromechanical transducers
[3-5], which are often operated at the high field regime
[6]. They are also very attractive to improve high per-
formance actuators and sensors design in advanced ap-
plications such as image ultrasonic system and sonar.
Unfortunately piezoceramics show a pronounced non-
linearity [7]. This phenomenon has a rather complex
physical origin. Nonlinearities appear as alterations of
elastic, electric and piezoelectric behavior [8]. Therefore,
many applications can benefit from a better understand-
ing of the ceramics performance under various electrical,
mechanical and temperature conditions. In this context,
several phenomenological models have been proposed to
explain the physical origin of the observed dielectric,
mechanical and piezoelectric anomalies [9]. Nevertheless,
none of the models has gained universal acceptance yet,
due to some contradictory experimental results, as for
example the different behavior observed in soft and hard

D. KOBOR ET AL.
212
lead zirconate titanate ceramics (PZT).
PMN-PT system shows, from the fundamental point of
view, intriguing physical properties, which are reflected
in the dielectric response. However, in this system, there
are ambiguous reports concerning the existence and ori-
gin of the observed dielectric behavior under external
applied electric fields [10], although it is widely accepted
that one of their origin is the movement of the domain
walls [9]. In a recent work, dielectric and piezoelectric
nonlinear responses of PMN-35PT ceramics were inves-
tigated [11]. Results showed typical soft-type behaviour,
with high linear properties (dielectric and piezoelectric
coefficients). However, it is necessary to improve the
performance of this system for typical hard-type piezo-
ceramics applications. In this sense, the objective of this
work is to study and to understand the effect of Mn dop-
ing on PMN-35PT in order to improve the dielectric and
mechanical responses of this system for high power ap-
plication.
2. Experimental Procedure
0.65 [Pb (Mg1/2Nb2/3)] O3-0.35PbTiO3 ceramics doped
with 1%Mn, hereafter labeled as PMN-35PT + 1%Mn,
were prepared by using fine powders, as previously re-
ported [12]. High purity chemical powders PbO (99%
QS), TiO2 (99% Merck), MgO (99% Merck), Nb2O5
(99.9% Aldrich) were used as starting materials. The
PMN-PT ceramics were synthesized using the two-step
columbite precursor technique. Powders of Magnesium
oxide (MgO) and Niobium oxide (Nb2O5) were mixed in
alcohol, using MgO excess, ground and calcined at
1100˚C for 8 hours in order to synthesize MgNb2O6
phase. Magnesium niobate was mixed with the MnO2,
PbO and TiO2 in the ratio of PMN-PT 65-35 in molar
percentage. Small excess of PbO was added to compen-
sate its loss during heat treatments. This mixture was
calcined at 825˚C for 2 hours. The resulting mixture of
1%Mn + PMN-PT powder was mixed with 10 wt %
polyvinyl alcohol (PVA) solution, and was pressed to
prepare pellets with 13 mm of diameter and 1,2 mm of
thickness with a 80 MPa uniaxial stress. The pellets were
first heated at 600˚C to burn out the PVA, and then sin-
tered at 1250˚C for 10 hours in a sealed alumina crucible
with 5 g of PbZrO3 to prevent lead losses during sinter-
ing. A pure perovskite phase of 1%Mn doped PMN-PT
was obtained.
With this amount of dopant, polycrystalline PZT ce-
ramics show a high increase of quality factor (Qm) with-
out significantly decreasing the piezoelectric coefficients
[13]. X-ray powder diffraction was performed on sin-
tered ceramics with the help of a Philips X’pert Pro dif-
fractometer using a monochromatic CuKα radiation (λ =
1.5418 Å). Scanning electronic microscopy techniques
was carried out by using a JMS 840 (JEOL). An EPR
VARIAN E19 spectrometer was used to determine the
Manganese valences.
The samples were obtained in the form of discs with
13 mm of diameter and 1 mm of thickness. Parallel faces
were sputtered with silver for functional properties
measurements. Poling was performed with an electric
field of 3 kV/cm during 30 minutes at room temperature.
Dielectric properties were determined as a function of
temperature by using a multi-frequency LCR meter
(HP4284A) and a computer-controlled temperature
chamber. From these plots (not published), the phase
transition temperature (Tc) and the room temperature
dielectric properties were identified. The longitudinal
mode piezoelectric coefficient d33 was measured with the
help of a Berlincourt d33 meter. Electromechanical prop-
erties were calculated from the resonance peak meas-
urement.
Table 1 summarizes the dielectric, piezoelectric and
electromechanical coefficients of undoped and 1%Mn
doped PMN-35PT ceramics. The dielectric and piezo-
electric properties decrease with the doping while the
mechanical quality factor Qm increases largely (78 to
317). Such behavior is found in literature for hard ce-
ramics [3]. This fact suggests that Mn addition induces
some mechanisms that turn the PMN-PT properties from
soft- to hard-type.
2.1. Dielectric and Mechanical Nonlinearities
The non-linear dielectric measurements are made at 1
kHz, by a modified comparison capacitance bridge that
Table 1. Dielectric, piezoelectric and electromechanical properties of undoped and 1% Mn doped PMN-35PT ceramics at
room temperature. Curie temperatures are also reported. Dielectric measurements have been carried out at 1 kHz.
d33
(pC/N) KP K
t SE
11
(10-12 m2/N) L tane (%) Qm c (˚C)
PMN-35PT 650 [5]
595 [3]
0,50 [3] 0,57 [5]
0,60 [2]
13,30 [1]
19,00 [4]
3800 [1]
4220 [5]
0,60 [1]
1,96 [3]
78 [4]
78 [5]
165 [1]
170 [6]
PMN-35PT+1%Mn 405
455 [3]
0,49
0,48 [3]
0,51
-
10,30
11,00 [4]
2074
2100 [4]
0,53
0,78 [3]
317
300 [4]
175
175 [4]

D. KOBOR ET AL.
213
is compensated at low signal in order to obtain the
nonlinear contribution to the electric displacement DNL(E),
and consequently the nonlinear dielectric constant in-
crement, ΔεNL (E, E0), as a function of instantaneous
electric field, E. To prevent overheating of the ceramics
due to the high signal excitation, burst signal excitations
with only 5 cycles are used. After subtraction of the an-
tisymmetric contribution εA (a low contribution that de-
pends on the polarization), the symmetric contribution εS
is analyzed. This term is divided again into two contribu-
tions: the first, εα, depends only to the electric field am-
plitude, and the second, εβ, is the remaining contribution,
which depends on the instantaneous electric field, as is
detailed in Ref. [14]. The increment of dielectric constant
has been written as follow:
ΔεNL (E, E0) = εΑ (E, E0) + εS (E, E0) = εΑ (E, E0) + εα (E0)
+ εβ (E, E0). (1)
For PZT based piezoceramics, the contribution εα has
been satisfactorily associated to irreversible contribution
of domain wall motion, while εβ represents a reversible
contribution which has been related to the bending of
domain walls [15].
Measurements of mechanical nonlinearities have been
obtained by exciting the 1st radial mode of resonance.
Bursts of different amplitudes and equal frequency, close
to the resonant frequency, were applied, by measuring
the electrical impedance [16]. The increase of the real
part of impedance are related to the increase of me-
chanical losses Δtg (δm), while the increase of the
imaginary part is related to the shift of the resonant fre-
quency, and thus it is related to the increase of the com-
pliance 11
E
s
. The vibration velocity of the border of the
disc v(R) has also been measured by using a laser vi-
brometer, in order to obtain the mean strainS.
From these measurements it is possible to obtain the
values of the motional electrical displacement Dm =
Im/Aω, and the main stress T, defined as follows:


11
2,
.
1
r
rE
vR
SSS R
S
TTT s






Finally, the piezoelectric coefficient d31 is obtained as
a ratio between dielectric displacement and the main
stress, d31 = Dm/T, assuming that in the resonance the
electric field is null.
3. Results and Discussions
3.1. Structural Characterization
Figure 1 shows the XRD diffraction patterns, which con-
firm a pure perovskite phase with a majority tetragonal
symmetry for PMN-PT + 1%Mn. No residual phases are
detected. Generally, XRD diagrams are carried out over
narrow angular regions centered about the six pseudo-cubic
reflections (100), (110), (111), (200), (220) and (222),
from which it is possible to determine unambiguously
the crystal’s symmetry [17]. It is clear that the tetragonal
symmetry is characterized by the presence of the (h00)
doubled peaks. In our case, from the peaks profiles of the
(100) and (200) reflections, the symmetry is clearly seen
to be tetragonal with a possible presence of a rhombo-
hedral symmetry. This structure is the same that recently
has been published by Guerra et al. for PMN-35PT ce-
ramics [10].
These results show that the 1% mol Mn doping didn’t
change the PMN-35PT ceramics structure at room tem-
perature.
SEM images revealed a homogeneous grain size dis-
tribution and morphology for PMN-35PT + 1%Mn as
can be shown in Figure 2. This image confirms that
there exists no pyrochlore phase grain, which is charac-
terized by its pyramidal form. The micro-structural mor-
phology presents an average grain size between 3 to 8
μm for the undoped PMN-35PT ceramics [12] and 6 to 8
μm for the Mn doped ones.
Figure 3 shows the EPR spectrum for PMN-35PT +
1%Mn. Two peaks are detected at about 1800 and 3200
G which are attributed, respectively, to the Mn4+ and
Mn2+ ions, confirming that the major part of Mn is at its
lower valence 2+. The presence of Mn4+ can be seen,
while it is impossible to prove with this technique the
presence of Mn3+ which has an anti-parallel spin. The
Mn2+ peak forms a sextet. This is due to the hyperfine
interaction in the structure for which the most important
contributor is the spin-orbit coupling. These 6 hyperfine
lines are due to the degenerated energetic states (mI = 5/2,
3/2, 1/2, –1/2, –3/2 and –5/2)
Figure 1. X-Ray Diffraction patterns of 1% mol Mn doped
PMN-35PT ceramics.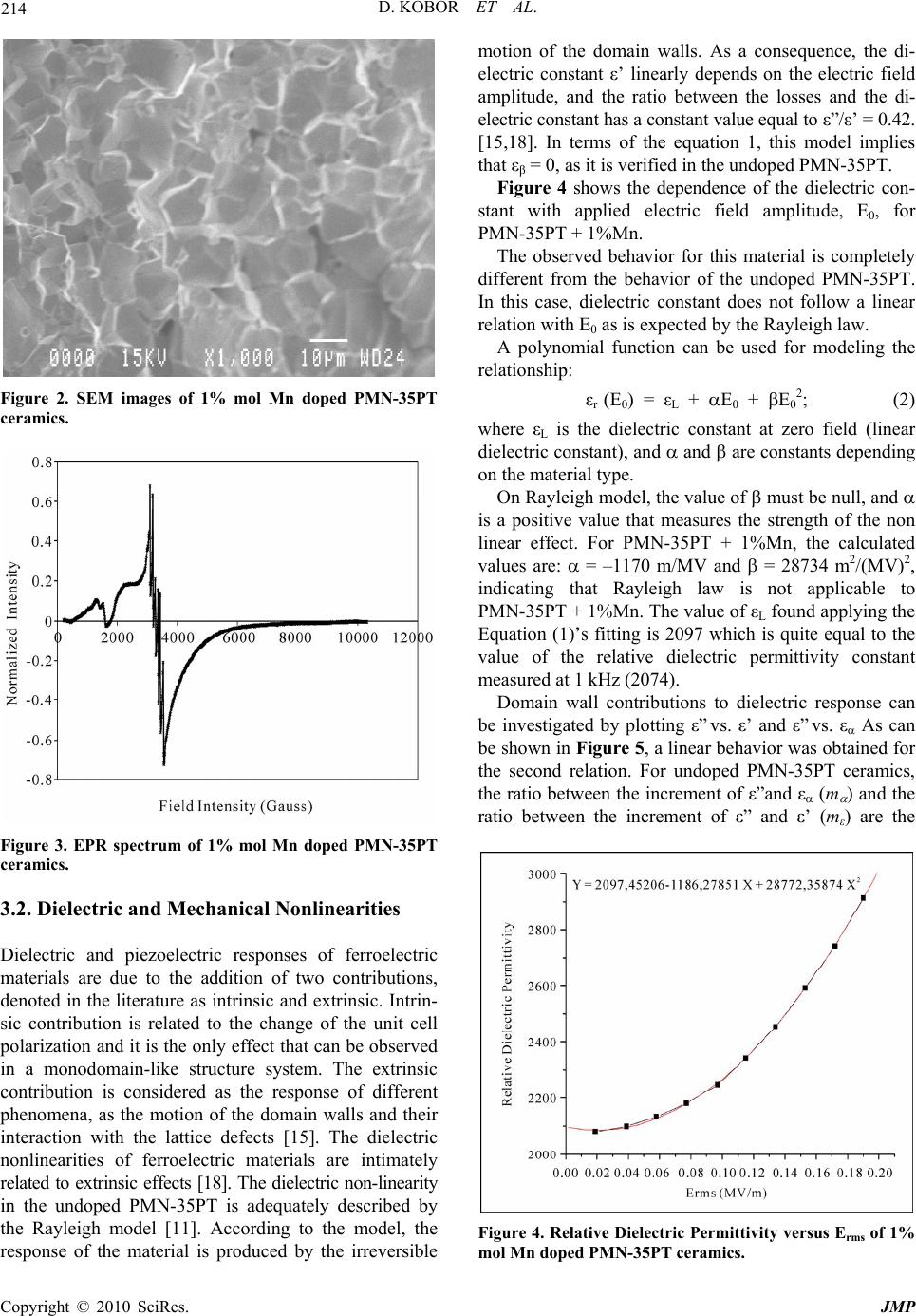

D. KOBOR ET AL.
214
Figure 2. SEM images of 1% mol Mn doped PMN-35PT
ceramics.
Figure 3. EPR spectrum of 1% mol Mn doped PMN-35PT
ceramics.
3.2. Dielectric and Mechanical Nonlinearities
Dielectric and piezoelectric responses of ferroelectric
materials are due to the addition of two contributions,
denoted in the literature as intrinsic and extrinsic. Intrin-
sic contribution is related to the change of the unit cell
polarization and it is the only effect that can be observed
in a monodomain-like structure system. The extrinsic
contribution is considered as the response of different
phenomena, as the motion of the domain walls and their
interaction with the lattice defects [15]. The dielectric
nonlinearities of ferroelectric materials are intimately
related to extrinsic effects [18]. The dielectric non-linearity
in the undoped PMN-35PT is adequately described by
the Rayleigh model [11]. According to the model, the
response of the material is produced by the irreversible
motion of the domain walls. As a consequence, the di-
electric constant ε’ linearly depends on the electric field
amplitude, and the ratio between the losses and the di-
electric constant has a constant value equal to ε”/ε’ = 0.42.
[15,18]. In terms of the equation 1, this model implies
that εβ = 0, as it is verified in the undoped PMN-35PT.
Figure 4 shows the dependence of the dielectric con-
stant with applied electric field amplitude, E0, for
PMN-35PT + 1%Mn.
The observed behavior for this material is completely
different from the behavior of the undoped PMN-35PT.
In this case, dielectric constant does not follow a linear
relation with E0 as is expected by the Rayleigh law.
A polynomial function can be used for modeling the
relationship:
εr (E0) = εL + E0 + E02; (2)
where εL is the dielectric constant at zero field (linear
dielectric constant), and  and  are constants depending
on the material type.
On Rayleigh model, the value of  must be null, and 
is a positive value that measures the strength of the non
linear effect. For PMN-35PT + 1%Mn, the calculated
values are:  = –1170 m/MV and  = 28734 m2/(MV)2,
indicating that Rayleigh law is not applicable to
PMN-35PT + 1%Mn. The value of εL found applying the
Equation (1)’s fitting is 2097 which is quite equal to the
value of the relative dielectric permittivity constant
measured at 1 kHz (2074).
Domain wall contributions to dielectric response can
be investigated by plotting ε” vs. ε’ and ε” vs. ε As can
be shown in Figure 5, a linear behavior was obtained for
the second relation. For undoped PMN-35PT ceramics,
the ratio between the increment of ε”and ε (m

) and the
ratio between the increment of ε” and ε’ (mε) are the
Figure 4. Relative Dielectric Permittivity versus Erms of 1%
mol Mn doped PMN-35PT ceramics.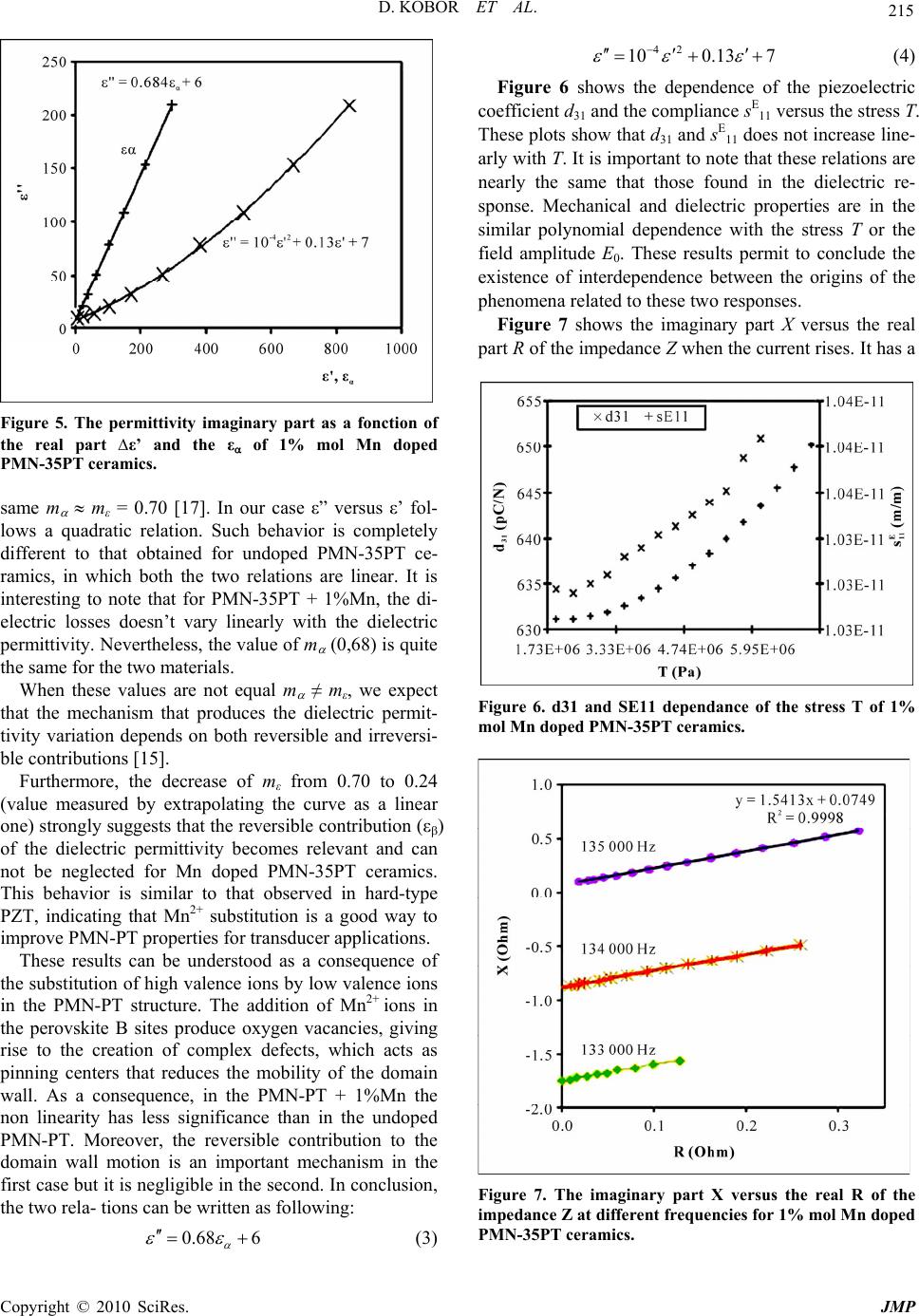

D. KOBOR ET AL.
215
Figure 5. The permittivity imaginary part as a fonction of
the real part ∆ε’ and the ε of 1% mol Mn doped
PMN-35PT ceramics.
same m

 mε = 0.70 [17]. In our case ε” versus ε’ fol-
lows a quadratic relation. Such behavior is completely
different to that obtained for undoped PMN-35PT ce-
ramics, in which both the two relations are linear. It is
interesting to note that for PMN-35PT + 1%Mn, the di-
electric losses doesn’t vary linearly with the dielectric
permittivity. Nevertheless, the value of m

(0,68) is quite
the same for the two materials.
When these values are not equal m

≠ mε, we expect
that the mechanism that produces the dielectric permit-
tivity variation depends on both reversible and irreversi-
ble contributions [15].
Furthermore, the decrease of mε from 0.70 to 0.24
(value measured by extrapolating the curve as a linear
one) strongly suggests that the reversible contribution (ε)
of the dielectric permittivity becomes relevant and can
not be neglected for Mn doped PMN-35PT ceramics.
This behavior is similar to that observed in hard-type
PZT, indicating that Mn2+ substitution is a good way to
improve PMN-PT properties for transducer applications.
These results can be understood as a consequence of
the substitution of high valence ions by low valence ions
in the PMN-PT structure. The addition of Mn2+ ions in
the perovskite B sites produce oxygen vacancies, giving
rise to the creation of complex defects, which acts as
pinning centers that reduces the mobility of the domain
wall. As a consequence, in the PMN-PT + 1%Mn the
non linearity has less significance than in the undoped
PMN-PT. Moreover, the reversible contribution to the
domain wall motion is an important mechanism in the
first case but it is negligible in the second. In conclusion,
the two rela- tions can be written as following:
0.68 6



 
(3)
42
100.13 7  


 

 (4)
Figure 6 shows the dependence of the piezoelectric
coefficient d31 and the compliance sE11 versus the stress T.
These plots show that d31 and sE11 does not increase line-
arly with T. It is important to note that these relations are
nearly the same that those found in the dielectric re-
sponse. Mechanical and dielectric properties are in the
similar polynomial dependence with the stress T or the
field amplitude E0. These results permit to conclude the
existence of interdependence between the origins of the
phenomena related to these two responses.
Figure 7 shows the imaginary part X versus the real
part R of the impedance Z when the current rises. It has a
Figure 6. d31 and SE11 dependance of the stress T of 1%
mol Mn doped PMN-35PT ceramics.
Figure 7. The imaginary part X versus the real R of the
impedance Z at different frequencies for 1% mol Mn doped
PMN-35PT ceramics.

D. KOBOR ET AL.
216
linear dependence with a slope m around 3/2. The in-
verse of this slope, 1/m, is the same as the value of m

found in Figure 5 (2/3 = 0.67). This relationship between
these two properties shows that there is an interdepend-
ence of the phenomena that lie behind them.
4. Conclusion
In this study, the effect of Mn doping on the structural
and non-linear dielectric and mechanical properties for
PMN-35PT ceramics is shown. It can be concluded that
1% mol Mn doping does not change the phase structure
and grain morphology of PMN-35PT ceramics. EPR
studies show that Manganese was present in majority in
its lower valence 2+, achieving a large increase of elec-
tromechanical quality factor while keeping good values
of the dielectric and piezoelectric properties. The Mn
doped ceramics do not follow the Rayleigh law, indicat-
ing that in this case the reversible movement of domain
wall is a relevant contribution to material response. Re-
sults of this work demonstrate that Mn doping is a good
way to obtain new compounds of PMN-PT systems with
better properties for high power applications.
5. References
[1] G. A. Smolenskii and A. I. Agranovskaya, “Dielectric
Polarization and Losses of Some Complex Compounds,”
Soviet Physics Technical Physics, Vol. 3, No. 3, 1958, pp.
1380-1389.
[2] Y. H. Chen, K. Uchino and D. Viehland, “Substituent
Effects in 0.65Pb (Mg1/3Nb2/3)O3–0.35PbTiO3 Ceram-
ics,” Journal of Electroceramics, Vol. 6, No. 1, 2001, pp.
13-17.
[3] M. E. Lines and G. M. Glass, “Principles and Applica-
tions of Ferroelectrics and Related Materials,” Oxford
University Press, Oxford, United Kingdom, 2001, p. 77.
[4] S. E. Park and T. R. Shrout, “Ultrahigh Strain and Piezo-
electric Behavior in Relaxor Based Ferroelectric Single
Crystals,’’ Journal of Applied Physics, Vol. 82, No. 4,
1997, pp. 1804-1811.
[5] S. W. Choi, T. R. Shrout, S. J. Jang and A. S. Bhalla,
“Morphotropic Phase Boundary in Pb(Mgl/3 Nb2/3-
PbTiO3 System,” Materials Letters, Vol. 8, No. 6-7, 1989,
pp. 253-255.
[6] H. Takagi, K. Sakata and T. Takenaka, “Electrostrictive
Properties of Pb(Mg1/3Nb2/3)O3-Based Relaxor Ferroelec-
tric Ceramics,” Japanese Journal of Applied Physics, Vol.
32, No. 9S, 1993, pp. 4280-4283.
[7] D. A. Hall, “Nonlinearity in Piezoelectric Ceramics,”
Journal of Material Sciences, Vol. 36, No. 19, 2001, pp.
4575-4601.
[8] D. Kobor, A. Albareda, R. Perez, J. Garcia, L. Lebrun
and D. Guyomar, “Dielectric and Mechanical Nonlineari-
ties of <001> Oriented Pure and Doped Single Crystals of
PZN-4.5PT,” Journal of Physics D: Applied Physics, Vol.
38, No. 13, 2005, pp. 2258-2264.
[9] A. K. Tangsev and A. E. Glazounov, “Mechanism of
Polarization Response in the Ergodic Phase of a Relaxor
Ferroelectric,’’ Physical Review B, Vol. 57, No. 1, 1998,
pp. 18-21.
[10] J. D. S. Guerra, E. B. Araújo, C. A. Guarany, R. N. Reis
and E. C. Lima, “Features of Dielectric Response in
PMN–PT Ferroelectric Ceramics,” Journal of Physics D:
Applied Physics, Vol. 41, No. 22, 2008, pp. 225504-
225508.
[11] J. E. Garcia, J. D. S. Guerra, E. B. Araújo and R. Pérez,
“Domain Wall Contribution to Dielectric and Piezoelec-
tric Responses in 0.65Pb(Mg1/3Nb2/3)–0.35PbTiO3 Ferro-
Eectric Ceramics,’’ Journal of Physics D: Applied Physics,
Vol. 42, No. 11, 2009, pp. 115421-115425.
[12] A. Benayad, ‘‘Matériaux Monocristallins à Forte Activité
Piézoélectrique: élaboration, Caractérisation et Application,’’
Thesis, INSA, December 2005, p. 155.
[13] L. Lebrun, B. Guiffard, E. Boucher, D. Audigier, D.
Guyomar, L. Eyraud and E. Pleska, “Dielectric and Pie-
zoelectric Properties of (La, Mg, F) and (Mg, Mn, F)
Doped PZT Ceramics under Low and High Solicitations,”
Journal of the European Ceramic Society, Vol. 21, No.
10-11, 2001, pp. 1357-1360.
[14] J. E. Garcia, R. Pérez and A. Albareda, “High Electric
Field Measurement of Dielectric Constant and Losses of
Ferroelectric Ceramics,’’ Journal of Physics D: Applied
Physics, Vol. 34, No. 22, 2001, pp. 3279-3284.
[15] J. E. Garcia, R. Pérez and A. Albareda, “Contribution of
Reversible Processes to the Non-Linear Dielectric Re-
sponse in Hard Lead Zirconate Titanate Ceramics,” Journal
of Physics: Condensed Matter, Vol. 17, No. 44, 2005, pp.
7143-7150.
[16] J. A. Casals, A. Albareda, R. Pérez, J. E. García, E.
Minguella and F. M. de Espinosa, “Nonlinear Charac-
terization with Burst Excitation of 1-3 Piezocomposites
Transducers,” Ultrasonics, Vol. 41, No. 4, 2003, pp. 307-
311.
[17] A. Benayad, D. Kobor, L. Lebrun, B. Guiffard and D.
Guyomar, “Characteristics of Pb[(Zn1/3Nb2/3)0.955Ti0.045]
O3 Single Crystals Versus Growth Method,” Journal of
Crystal Growth, Vol. 270, No. 1-2, 2004, pp. 137-144.
[18] D. Damjanovic and M. Demartin, “Contribution of the
Irreversible Displacement of Domain Walls to the Piezo-
electric Effect in Barium Titanate and Lead Zirconate Ti-
tanate Ceramics,” Journal of Physics: Condensed Matter,
Vol. 9, No. 23, 1997, pp. 4943-4953.