Journal of Modern Physics, 2010, 1, 300-302
doi:10.4236/jmp.2010.15042 Published Online November 2010 (http://www.SciRP.org/journal/jmp)
Calculation of the Masses of All Fundamental Elementary
Particles with an Accuracy of Approx. 1%
Karl Otto Greulich
Fritz Lipmann Institute Beutenbergstr. 11 D 07745 Jena, Germany
Received August 9, 2010; revised September 14, 2010; accepted September 29, 2010
Abstract
The masses of a l l fundamental elementary particles (those with a lifetime > 10-24 sec) can be calculated with
an inaccuracy of approx. 1% using the equation m/melectron = N/2α where α is the coupling constant of quan-
tum electrodynamics (also known as fine structure constant) (= 1/137.036), and N is an integer variable. This
is the by far most accurate and most comprehensive approach to calculate the particle masses.
Keywords: Particle Masses, Fine Structure Constant
1. Introduction
While theories of elementary particles are accurate in
determining decay channels and finding particle-multiplets,
calculation of particle masses is less successful. The
reason is that the masses of the constituting quarks can-
not be simply added up — binding energies need to be
considered which often exceed quark masses considera-
bly. A comprehensive theory on particle masses is not
available. Occasionally, the mass of one given elemen-
tary particle is predicted by a theory, but an accuracy in
the 10% regime is considered already as satisfying. Bet-
ter accuracies are only achieved when a theory is re-
stricted to subsets of the elementary particles, for exam-
ple the octet of mesons (the two pions and the four kaons)
or the decuplet of baryons (delta, sigma xi, omega). Very
good mass predictions have been obtained for the proton
and its excited states. A quark model with one-gluon-
exchange gives an accuracy of 5.6% [1], an alternative
model using “instantons” yields 5.1% [2] and, as the best,
the AdS/QCD model using di-quarks has an accuracy of
2.5% [3]. For an overview on these theories in German
language see [4].
In contrast to those approaches, the present contribu-
tion aims at finding a simple rule which allows to give
the masses of a l l fundamental elementary particles with
reasonable accuracy. A first attempt had been made ear-
lier, however with errors of several percent particularly
for the light particles [5].
2. Basic Data
There are 36 elementary particles with lifetimes longer
than 10-24 sec. All others have shorter lifetime which are
usually determined not by direct time measurements but
by determining their line width. A lifetime of less than
10-24 sec means that such a short living particle, even
when moving with a speed close to that of light, cannot
migrate even one own diameter before it decays. Table 1
gives the masses of all “fundamental” elementary parti-
cles:
All leptons have negative charge. For mesons with dif-
ferent charge, both charged mesons have the same mass.
For baryons the following applies: mpositive < mneutral <
mnegative (except for the double positive sigmac). Gener-
ally, the masses of the differently charged versions of a
particle differ by less than 1%, except for the pion, where
the difference is 3.5%. In the following, the particle
variant with the longest lifetime (printed bold in Table 1)
is taken as representative, with the exception of the kaon,
where the mass of K+/- (lifetime 1.238 × 10-8 sec) is used
instead of the mass of KL
0 (slightly higher lifetime 5.18 ×
10-8 sec). The reason for using the mass of a variant with
longest lifetime is that the present approach is not yet
accurate enough to distinguish between charged and non
charged versions of a particle.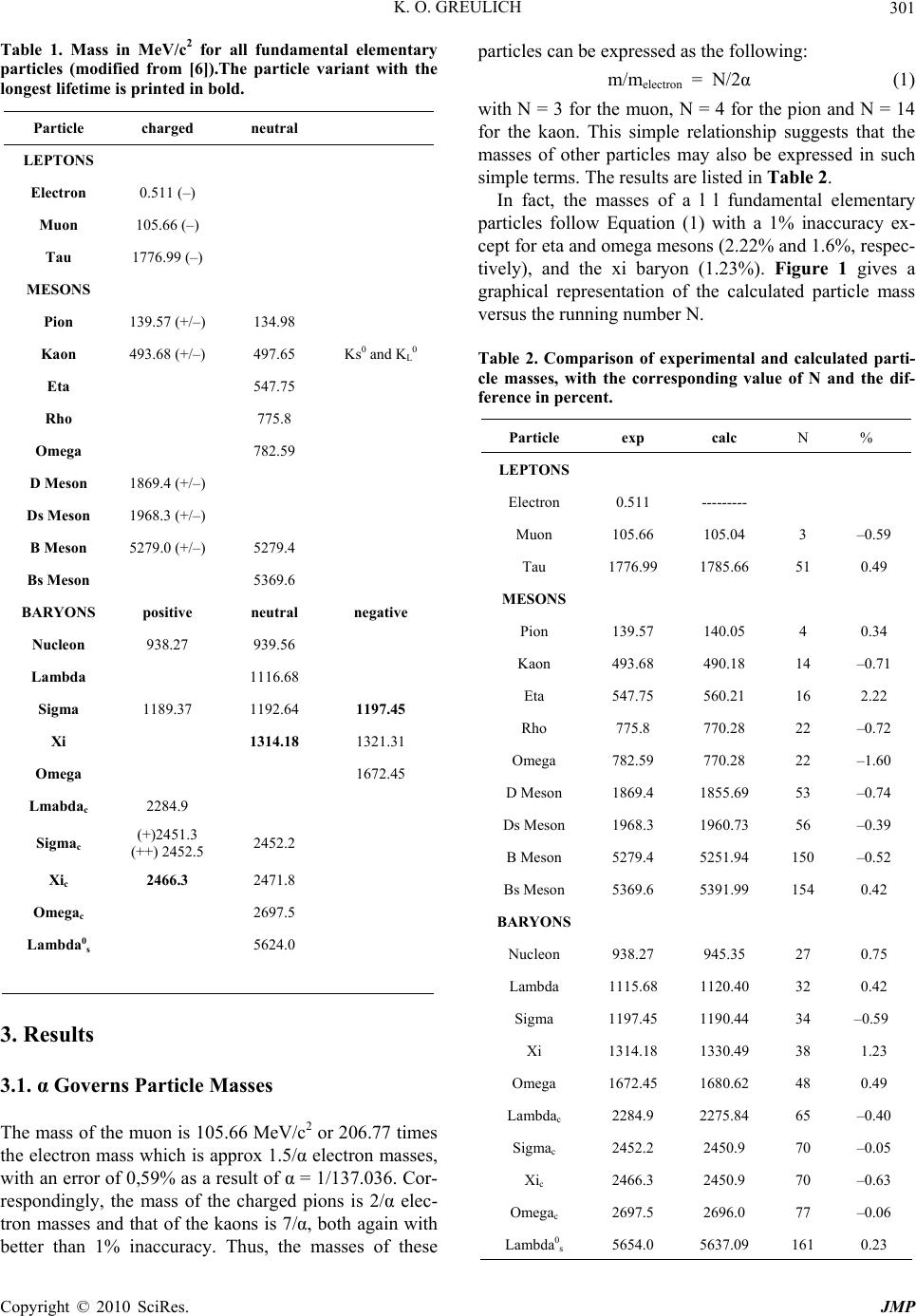

K. O. GREULICH 301
Table 1. Mass in MeV/c2 for all fundamental elementary
particles (modified from [6]).The particle variant with the
longest lifetime is printed in bold.
Particle charged neutral
LEPTONS
Electron 0.511 (–)
Muon 105.66 (–)
Tau 1776.99 (–)
MESONS
Pion 139.57 (+/–) 134.98
Kaon 493.68 (+/–) 497.65 Ks0 and KL0
Eta
547.75
Rho
775.8
Omega 782.59
D Meson 1869.4 (+/–)
Ds Meson 1968.3 (+/–)
B Meson 5279.0 (+/–) 5279.4
Bs Meson 5369.6
BARYONS positive neutral negative
Nucleon 938.27 939.56
Lambda 1116.68
Sigma 1189.37 1192.64 1197.45
Xi 1314.18 1321.31
Omega
1672.45
Lmabdac 2284.9
Sigmac (+)2451.3
(++) 2452.5 2452.2
Xic 2466.3
2471.8
Omegac 2697.5
Lambda0
s 5624.0
3. Results
3.1. α Governs Particle Masses
The mass of the muon is 105.66 MeV/c2 or 206.77 times
the electron mass which is approx 1.5/α electron masses,
with an error of 0,59% as a result of α = 1/137.036. Cor-
respondingly, the mass of the charged pions is 2/α elec-
tron masses and that of the kaons is 7/α, both again with
better than 1% inaccuracy. Thus, the masses of these
particles can be expressed as the following:
m/melectron = N/2α (1)
with N = 3 for the muon, N = 4 for the pion and N = 14
for the kaon. This simple relationship suggests that the
masses of other particles may also be expressed in such
simple terms. The results are listed in Table 2.
In fact, the masses of a l l fundamental elementary
particles follow Equation (1) with a 1% inaccuracy ex-
cept for eta and omega mesons (2.22% and 1.6%, respec-
tively), and the xi baryon (1.23%). Figure 1 gives a
graphical representation of the calculated particle mass
versus the running number N.
Table 2. Comparison of experimental and calculated parti-
cle masses, with the corresponding value of N and the dif-
ference in percent.
Particle exp calc N %
LEPTONS
Electron 0.511 ---------
Muon 105.66 105.04 3 –0.59
Tau 1776.99 1785.66 51 0.49
MESONS
Pion 139.57 140.05 4 0.34
Kaon 493.68 490.18 14 –0.71
Eta 547.75 560.21 16 2.22
Rho 775.8 770.28 22 –0.72
Omega 782.59 770.28 22 –1.60
D Meson 1869.4 1855.69 53 –0.74
Ds Meson 1968.3 1960.73 56 –0.39
B Meson 5279.4 5251.94 150 –0.52
Bs Meson 5369.6 5391.99 154 0.42
BARYONS
Nucleon 938.27 945.35 27 0.75
Lambda 1115.68 1120.40 32 0.42
Sigma 1197.45 1190.44 34 –0.59
Xi 1314.18 1330.49 38 1.23
Omega 1672.45 1680.62 48 0.49
Lambdac 2284.9 2275.84 65 –0.40
Sigmac 2452.2 2450.9 70 –0.05
Xic 2466.3 2450.9 70 –0.63
Omegac 2697.5 2696.0 77 –0.06
Lambda0s 5654.0 5637.09 161 0.23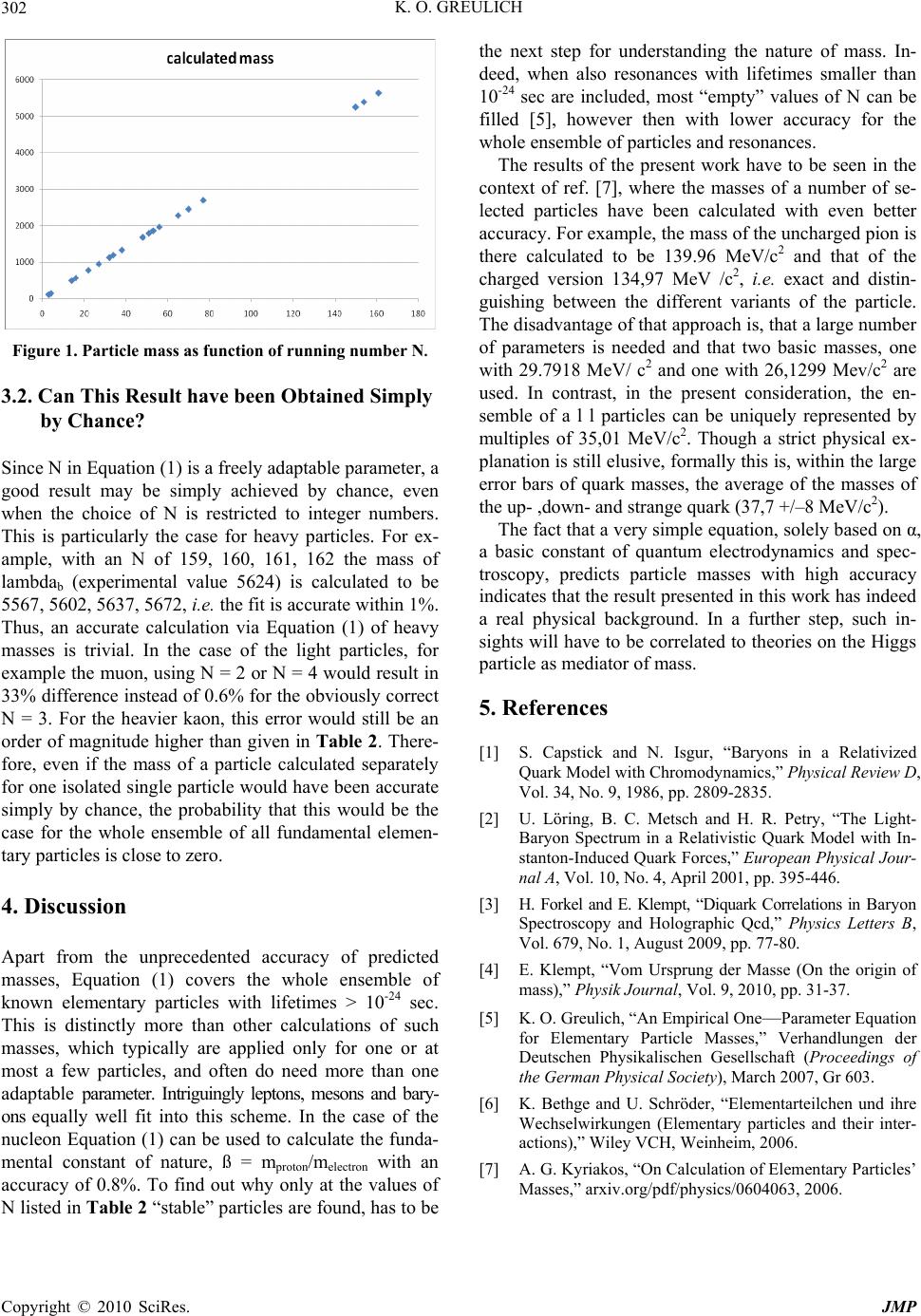

K. O. GREULICH 302
Figure 1. Particle mass as function of running number N.
3.2. Can This Result have been Obtained Simply
by Chance?
Since N in Equation (1) is a freely adaptable parameter, a
good result may be simply achieved by chance, even
when the choice of N is restricted to integer numbers.
This is particularly the case for heavy particles. For ex-
ample, with an N of 159, 160, 161, 162 the mass of
lambdab (experimental value 5624) is calculated to be
5567, 5602, 5637, 5672, i.e. the fit is accurate within 1%.
Thus, an accurate calculation via Equation (1) of heavy
masses is trivial. In the case of the light particles, for
example the muon, using N = 2 or N = 4 would result in
33% difference instead of 0.6% for the obviously correct
N = 3. For the heavier kaon, this error would still be an
order of magnitude higher than given in Table 2. There-
fore, even if the mass of a particle calculated separately
for one isolated single particle would have been accurate
simply by chance, the probability that this would be the
case for the whole ensemble of all fundamental elemen-
tary particles is close to zero.
4. Discussion
Apart from the unprecedented accuracy of predicted
masses, Equation (1) covers the whole ensemble of
known elementary particles with lifetimes > 10-24 sec.
This is distinctly more than other calculations of such
masses, which typically are applied only for one or at
most a few particles, and often do need more than one
adaptable parameter. Intriguingly leptons, mesons and bary-
ons equally well fit into this scheme. In the case of the
nucleon Equation (1) can be used to calculate the funda-
mental constant of nature, ß = mproton/melectron with an
accuracy of 0.8%. To find out why only at the values of
N listed in Table 2 “stable” particles are found, has to be
the next step for understanding the nature of mass. In-
deed, when also resonances with lifetimes smaller than
10-24 sec are included, most “empty” values of N can be
filled [5], however then with lower accuracy for the
whole ensemble of particles and resonances.
The results of the present work have to be seen in the
context of ref. [7], where the masses of a number of se-
lected particles have been calculated with even better
accuracy. For example, the mass of the uncharged pion is
there calculated to be 139.96 MeV/c2 and that of the
charged version 134,97 MeV /c2, i.e. exact and distin-
guishing between the different variants of the particle.
The disadvantage of that approach is, that a large number
of parameters is needed and that two basic masses, one
with 29.7918 MeV/ c2 and one with 26,1299 Mev/c2 are
used. In contrast, in the present consideration, the en-
semble of a l l particles can be uniquely represented by
multiples of 35,01 MeV/c2. Though a strict physical ex-
planation is still elusive, formally this is, within the large
error bars of quark masses, the average of the masses of
the up- ,down- and strange quark (37,7 +/–8 MeV/c2).
The fact that a very simple equation, solely based on α,
a basic constant of quantum electrodynamics and spec-
troscopy, predicts particle masses with high accuracy
indicates that the result presented in this work has indeed
a real physical background. In a further step, such in-
sights will have to be correlated to theories on the Higgs
particle as mediator of mass.
5. References
[1] S. Capstick and N. Isgur, “Baryons in a Relativized
Quark Model with Chromodynamics,” Physical Review D,
Vol. 34, No. 9, 1986, pp. 2809-2835.
[2] U. Löring, B. C. Metsch and H. R. Petry, “The Light-
Baryon Spectrum in a Relativistic Quark Model with In-
stanton-Induced Quark Forces,” European Physical Jour-
nal A, Vol. 10, No. 4, April 2001, pp. 395-446.
[3] H. Forkel and E. Klempt, “Diquark Correlations in Baryon
Spectroscopy and Holographic Qcd,” Physics Letters B,
Vol. 679, No. 1, August 2009, pp. 77-80.
[4] E. Klempt, “Vom Ursprung der Masse (On the origin of
mass),” Physik Journal, Vol. 9, 2010, pp. 31-37.
[5] K. O. Greulich, “An Empirical One—Parameter Equation
for Elementary Particle Masses,” Verhandlungen der
Deutschen Physikalischen Gesellschaft (Proceedings of
the German Physical Society), March 2007, Gr 603.
[6] K. Bethge and U. Schröder, “Elementarteilchen und ihre
Wechselwirkungen (Elementary particles and their inter-
actions),” Wiley VCH, Weinheim, 2006.
[7] A. G. Kyriakos, “On Calculation of Elementary Particles’
Masses,” arxiv.org/pdf/physics/0604063, 2006.