Communications and Network, 2010, 2, 235-245
doi:10.4236/cn.2010.24034 Published Online November 2010 (http://www.SciRP.org/journal/cn)
All-Optical Cryptographic Device for Secure
Communication
Fabio Garzia, Roberto Cusani
INFOCOM Department, SAPIENZA – Universi t y of Rome , Rome, Italy
Received March 3, 2010; revised May 7, 2010; accepted April 23, 2010
Abstract
An all-optical cryptographic device for secure communication, based on the properties of soliton beams, is
presented. It can encode a given bit stream of optical pulses, changing their phase and their amplitude as a
function of an encryption serial key that merge with the data stream, generating a ciphered stream. The
greatest advantage of the device is real-time encrypting – data can be transmitted at the original speed with-
out slowing down.
Keywords: Cryptographic Device, Security Device, Soliton Interaction, All-optical Switching, Spatial Soli-
ton, All-optical Device.
1. Introduction
The device described in this paper is capable of codify-
ing a given bit stream of optical pulses, changing their
phase and their amplitude as a function of an encryption
serial key that merges with the data stream, generating a
ciphered stream. It is based on the special properties of
spatial solitons that are, as well known, self-trapped op-
tical beams able to propagate without any change of their
spatial shape, thanks to the equilibrium, in a self-focus-
ing medium, between diffraction and nonlinear refraction
[1].
Their interesting properties have allowed to design a
certain number of spatial optical switches which utilize
the interaction between two bright or dark solito n beams,
and the waveguide structures induced by these interac-
tions [2-6]. Two distinct parallel solitons are generally
used as initial cond ition for such interactions. In fact it is
well known that when two distinct bright spatial solito ns
are launched parallel to each other, the interaction force
between them depends on their relative distance and their
phase [7,8].
A variety of useful devices can be thought and de-
signed using the properties of solitons. One of the most
important features is their particle-like behaviour and
their relative robustness to external distu rbs.
Interesting effects have been found in the study of
transverse effects of soliton propagation at the interface
between two nonlinear materials [9-11] or in a material
in the presence of a Gaussian refractive index profile,
that is in low perturbation regime [12].
It has been shown that it is possible to switch a so lito n,
in the presence of a transverse refractive index variation,
towards a fixed path, since the index variation acts as a
perturbation against which the soliton reacts as a particle,
moving as a packet without any loss of energy. This last
property makes possible to design useful all optical de-
vices such as a filter [13] or a high speed router [14],
thanks to the possibility of generating spatial soliton in
real material [15-17].
The general problem of encrypting the data transmit-
ted on an optical medium is very felt in the security field
[18-33].
The aim of the present work is to find a new approach
to this problem, stud ying a device that is able to increase
the security level of an optical channel, extending the
modulation also to the phase of the output pulses. It acts
as an amplitude/phase converter accepting two binary
modulated stream of pulses as inputs and generating a
unique phase modulated stream of pulses as output. The
first stream is related to the data stream while the second
stream is related to the serial cryptographic key. The
great advantage is that the device is totally passive,
which means that is does not need extra energy to work
properly. The working principle is shown in Figure 1.
In its basic geometry a soliton beam travels in a
waveguide which, in the plane between the cladding and
he substrate, has a distribution of refractive index which t

F. GARZIA ET AL.
236
Figure 1. Working principle of the device.
follows a triangular curve, with a modified parabolic
profile.
We start studying the general structure of the device.
Then the transv erse behaviour of a soliton in a triangular
profile [13], who se longitudinal profile is parabolic [1 4],
is discussed. Once the properties of motion are derived,
we investigate the structure from the global point of view,
deriving all the properties and the operative conditions,
that represents the scope of this paper.
2. Structure of the Device
To simplify the development of the theory we consider
only a 2-in-1-out device. The function of the device is to
generate a phase modulated pulse according to the dif-
ferent combinations of amplitude of input pulses, that
represent the data stream and the cryptographic stream.
In the following we briefly call them input 1 and input 2.
This is equal to say that, in the presence of two binary
inputs, the possible amplitude combinations are 4, and
the output pulse has to assume 4 different phase values,
without requesting auxiliary energy.
We suppose to work with soliton beams to use their
attracting or repelling properties [7] and their particular
behaviour when they propagate in a transverse refractive
index profile [13]. The structure we want to study is
shown in Figure 2.
We also suppose that the two input pulses enter in the
relative inputs of the device with the same phase. This is
not a restriction since any phase difference can be prop-
erly compensated.
Owed to the fact that we deal with equal streams of
pulses the last condition means that the input pulses are
characterised by the same amplitude.
The device is composed by 4 parts: the main
waveguide, the secondary waveguide, the delay branch
and the drain waveguide. The geometry and the refrac-
tive index values of these four components strictly de-
termine the features of th e device an d their values will be
designed as discussed in the following.
Let us analyse the behaviour of the device in the four
possible input situations. Since we deal with binary input
pulses we consider the two values of logical zero (ab-
sence of pulse) and logical one (presence of pulse). We
refer to them as zero and one.
The first situation is when the two inputs are equal to
zero. In this case, due to the passive nature of the device,
we obtain a zero in the output.
The second situation is when the first input is equal to
one and the second input is equal to zero. In this case, if
the refractive index of both the delay branch and the drain
waveguide is less or equal to the refractive index of the
main waveguide, the pulse propagates undisturbed and it
reaches the output, with a phase that is equal to the propa-
gation phase along the main waveguide. If the length of
this waveguide is properly chosen, according to the wave-
length of the beam, the phase of the output pulse is equal
to the phase of the input pulse. In the first situation there
was an absence of pulse and its phase value was virtually
equal to zero. In this case the phase value variation has
been chosen equal to zero but we are in the presence of a
pulse. The phase variation could anyway be chosen at will,
but we keep it fixed at zero for simplicity. The behaviour
of this kind of waveguide has al ready been studied [13].
Figure 2. Structure of the device.

F. GARZIA ET AL.
237
The third situation is when the first input is equal to
zero and the second input is equal to one. In this case,
since we are in the proper refractive index conditions of
the waveguide and the delay branch is properly shifted
with respect to the input point of the second ary wave, the
second input pulse is trapp ed in the main waveguide and
it reaches the output with a certain phase difference, that
we define later, with respect to the previous case due to
the fact that it propagates, in the initial part, into the
secondary waveguide.
The fourth situation is when both the inputs are equal
to one. In this case the two pulses meet at the converging
point between the main waveguide and the secondary
waveguide. In this case, since we are in soliton propaga-
tion condition, they can attract if their relative phase is
included between zero and /2 or between 3/2 and 2,
or they can repel if their relative phase is included be-
tween /2 and 3/2. If the length of the secondary
waveguide is chosen to generate a repulsive condition,
the two solitons propagate in the main waveguide prop-
erly separated until reaching the bifurcation point be-
tween the main waveguide, the delay branch and the
drain waveguide. At this point the two solitons detach:
the first one enters the delay branch while the second one
enters the drain wave guide.
The first soliton propagates in the delay branch ex-
periencing a phase variation that depends on the length
of the branch and therefore is properly selectable and can
be chosen different from the previous cases, generating
the fourth phase condition. The second pulse, on the
contrary, propagates in the drain waveguide where it
reaches the proper drain output.
The delay branch is composed by a properly modified
longitudinal parabolic waveguide, whose purpose is to
accept the beam from the main waveguide with an angle
that respects the paraxial approximation, to propagate it
changing its direction until reaching a straight longitudi-
nal direction and to reverse this sequence until carrying
the pulse inside the main wav eguide with a certain phase
difference. The behaviour of this modified parabolic
waveguide is studied later.
The situation is summarised in Table 1, where it is
also pointed out the pulse that reaches the output to pro-
vide more details about the working principles of the
device, even if we consider input pulses with the same
amplitude.
3. Properties of a Soliton in a Modified
Longitudinal Parabolic Waveguide
We want now to define the structure of the modified
parabolic waveguide composing the delay branch to find
its peculiar properties that allow the loop to work prop-
erly.
Table 1. Working scheme of the device.
N
Input 1
(Inten-
sity)
Input 2
(Inten-
sity)
Output
(Inten-
sity)
Output
Phase
Phase
condition
10 0 0 0 -
21
I 0 1 I 0 -
30 2
I 2 I 2

2
3
22


 
41
I 2 I 1 I 1,2

-
We choose this kind of waveguide because it is the
simplest curve that carries progressively th e solito n b eam
from a propagation angle that respects the paraxial ap-
proximation until an angle that respects a parallel longi-
tudinal propagation and vice versa.
This curve could be roughly approximated with a lin-
ear curve, but the final result would be a too sharp path,
since the soliton reaches the reversing point with a cer-
tain inclination. Further the parabolic path is the trajec-
tory followed from a soliton beam that is injected into a
linear transverse refractive index profile, that is the
transverse profile that we are going to consider.
Let us consider a soliton beam propagating in the
z-direction, whose expression of the field Q at the begin-
ning of the structure is:

  x-xCsech0, CxQ

(1)
where
x
is the pos ition of the centre of the bea m and
C is a real constant from which both the width and the
amplitude of the field depend. The variables x and z are
normalised with respect to the wavevector of the wave
and therefore they are adimensional quantities.
When the soliton beam is propagating in a triangular
transverse index profile, whose maximum value is 0
n

and whose maximum width is 2b, it is subjected to a
transverse acceleration equal to [13,14]:
2 0
2
T
n
a
b

C (2)
We use, for our analysis, a dynamic point of view, that
is to consider the step by step transverse relative position
of the waveguide with respect to the beam using the z
variable as a time parameter.
If


G
x
z is the position of the central part of the
wa vegu ide profile with respect to z, th e longitudinal for m
of the waveguide is chosen to be a modified parabolic:

2
2
2
Gzd
x
z
a a
 z (3)
where 'a' is a real constant responsible for the curvature
of the waveguide and 'd' is a real constant responsible for

238 F. GARZIA ET AL.
the position of the curve. Equation (3) can be better un-
derstood if it is expressed as a function of z, that is:
G
zaxdad  (4)
It is possible to see that it is positioned in the second
quadrant of the Cartesian plane, it has a vertical asymp-
tote at

G
x
zd when zad. It shows a gradu-
ally increasing derivative, growing from a starting angle
at x=0, chosen to be below the maximum angle allowed
from the paraxial approximation, until reaching a vertical
alignment at

G
x
zd, that is what we want to make
the device work properly. To respect this term it is nec-
essary to impose a certain condition to the ‘a’ and ‘d’
parameters, as we show later. A graphical representation
of (4) is shown in Figure 4 for a=16.9 and d=1.4.
The local inclination of the waveguide with respect to
the longitudinal axis z, can be regarded as the transverse
relative velocity of the waveguide that appears to the
beam that propagates longitudinally:

2
22
vG
G
dx zz
dz a a

d
(5)
Using (2) it is possible to calculate the transv erse rela-
tive velocity:
2 0
0
2
vz
BT
n
ad Cz
b



 (6)
and the position of the beam
22 0
0
v
z
BB
n
x
dC
b



z (7)
Equation (7) is valid for a propagation in the first
quadrant of Cartesian plane. Since we consider, in our
case, a propagation in the second quadrant, we must re-
verse the sign of the second member of the equation con-
sidered.
Figure 4. Graphical representation of the modified para-
bolic waveguide for a=16.9, d=1.4, in normalized units.
Initially the beam is positioned in the centre of the
waveguide. Since the waveguide appears to move, with
respect to an observer that follows the longitudinal direc-
tion, with a relative velocity ex pressed by (5), the soliton
beam enters in the constant acceleration zone, where its
velocity increases linearly with z. It also follows a para-
bolic trajectory, according to (7), until it remains in this
part of the wav e guide.
After that the beam has propagated for a certain z dis-
tance, two different situations may happen: the beam
leaves the acceleration zone without reaching the veloc-
ity of the waveguide at that z, or the beam acquires a
velocity that is greater than or equal to th e velocity of the
waveguide. The first event may called ‘detach situation’,
since the beam leaves the waveguide, while the second
one may be called ‘lock-in situation’ since the beam
reaches the other side of the waveguide where it is
stopped, reversing its path and so on.
At any value of z, as shown in Figure 3, the distance
B
G
d between the beam and the waveguide is:
22
2 02
22
20
2
2
2
BGB G
nC zd
dxx z
ba a
banC d
zz
a ab

 


 


z
b
(8)
A detach situation takes place when:
BG
d (9)
If we solve (9) with respect to z, we can calculate, if it
exists, the propagation distance where the detachment
begins:
22
0
22
0
D
ddbanC
zbanC
ab

 (10)
Figure 3. Relative distance waveguide-soliton at some
propagation distance z.

F. GARZIA ET AL.
239
The two solutions refer to the detach situation (when
the negative sign o f the root is considered) or to the first
cross of the centre of the waveguide in the lock-in situa-
tion (when the positive sign of the root is considered).
Studying the discriminator of (10) it is possible to derive
the value of the amplitude
D
C that divides the lock-in
values from the detach values:
12
0
1
Ddb
Can





(11)
It is possible to see, from (11), that the more the cur-
vature of the waveguide (‘a’ parameter) increases or the
more the refractive index decreases and the more
D
C
increase. This behaviour agrees with what one could ex-
pect.
We want now to calculate the inclination according to
which a soliton, whose amplitude is smaller than the de-
tach amplitude, leaves the waveguide. Since the men-
tioned angle is equal to the detach velocity, substituting
(11) into (6), we have:
1
tan v
D

 (12a)
and

2
0
22
0
2
vv (
DBD
nCa
z
banC


 d
22
0)dbanC (12b)
In Figure 5 it is shown the graphical behaviour of (12)
for a=16.9, d=1.4, b=0.25, . The detach
value
5
0110n

D
C can be calculated by means of (11) and it is
equal to 20.
Due to the absence of restrictions abou t the length L of
the waveguide, the lock-in value
D
C of the amplitude,
expressed from (11), does not depend on L. This means
that, given a certain waveguide whose length is equal to
L, we can obtain a lock-in value
D
C whose detachment
distance, calculated from (10), is longer than L. In this
situation, due to the restriction imposed from the
waveguide length L, the detach value
D
C obviously
decreases. In fact, even if the beams characterised from
an amplitude lesser than
D
C tend to be expelled from the
waveguide, the detachment takes place at a distance that
is longer than the waveguide length L and the beam re-
mains locked-in. The new value
D
C, that is lower than
D
C, can be calculated from (10) setting D zL

and
solving respect to C:
24
2
DL BB AC
CA
 
 (13a)
where
422
0
A
anL (13b)
22 342
00
22BabLn abdLnabn
0

  (13c)
22 223
2CbL abLdab  (13d)
We want now to make some considerations about the
paraxial approximation.
Since we deal with a modified parabolic waveguide,
we are in the presence of a curvature, with respect to the
z axis, that increases with z. We have not to forget that
we are in a paraxial approximation, that is the derived
equations are valid until the angle between the propaga-
tion direction and the longitudinal direction is lesser than
8°10°. This means that, due to the analytical expression
of the waveguide, expressed from (3) or (4), once the ‘a’
or ‘d’ parameter has been chosen the other parameter is
unavoidably fixed. The condition must be imposed only
at the entrance of the waveguide, where the curvature,
with respect to the longitudinal direction is maximum
and decreases up to zero at the end. In analytical terms
this means that it is possible to impose this condition to
the first derivative of (3) to calculate the maximum
propagation distance:

2
0tan8
Gd
xa
0,14
(14)
that gives:
2
710
d
a

 (15)
This condition must be considered in the project of the
delay branch .
We want now to calculate the length of the curve ex-
pressed by (3), since it is necessary to control the optical
path, and therefore the phase variation, of the beam that
propagates inside it.
Considering (4), the first derivative of z with respect
to x is:
Figure 5. Detach angle  in degrees, equal to atan (vD),
versus C for a=16.9, d=1.4, b=0.25, Δn=1·10-5.

240 F. GARZIA ET AL.
2
dz a
dx
x
d
  (16)
and the elementary length of the curve, as a function of x
is:

2
22 2
4
a
dldx dzdxdx
xd


2
(17)
Integratin g (1 7 ) we have :
 
2
2
44
log(8 8
28
xda
xd a
xd
I
x


xd

2
244
4) constant
xda
axd xd

 
 (18)
It is possible to see that the integral becomes indefinite
when x tends to -d, as one could expect due to the struc-
ture of the curve. To define the constant that is present in
Equation (18) it is necessary to calculate the limit of the
integral when x tends to -d:

2
lim log
4
xd
a
I
x
 a (19)
The length of the curve is therefore equal to:


22 2
222
4
0log
28
44
4)4)l
4
Gddaa
LI da
d
dadaa
dd
dd




8
oga

(20)
that is obviously a complex function of ‘a’ and ‘d’ pa-
rameters.
4. Numerical Simulation of the Effect
We have simulated the device from the numerical point
of view using a FD-BPM algorithm to study its behav-
iour and to see if it agrees with the developed theory.
At first the design does not consider the physical limi-
tations that can arise when we deal with technological
fabrication problems. In the next paragraph we will con-
sider this kind of pro bl ems.
We use, in this situation, a geometrical approach, that
is we do not care of imposing particular conditions that
would be necessary in a real situation, such us to use the
same 0 for all the waveguides, letting us a higher
number of degrees of freedom. We are further free of
using the wavelength we need to generate the proper
phase variation according to our needs. This is not obvi-
ously possible in a real case where the wavelength is
given.
n
Let us choose for example the half length of the delay
branch waveguide equal to 20:
20ad (21)
Since we have to respect, even in this design approach,
the paraxial condition, we have to solve the system of
equations composed by (21) and (15) that gives a = 16.9,
d=1.4.
The width of the waveguide must obviously be less
than ‘d’ and we choose, for example b = 0.25, that is to
suppose a waveguide width equal to 2b = 0.5.
The spot size of the beam must be less or equal to ‘b ’.
Since we deal with a hyperbolic secant profile, expressed
by (1), the width is linked to the amplitude C, that is the
greater is C the narrower is the beam. A proper value is
C = 20.
The difference of length between the interested part of
the main waveguide and the delay branch can be calcu-
lated using (20) that gives . Once chosen
the wavevector we have immediately the phase differ-
ence.
0.1305
G
L
We have not, until this point, chosen the phase values
to code. We decide to generate a phase difference a bit
greater than /2 for the passage through the secondary
waveguide and a phase difference greater than  for the
passage through the delay branch. This is equal to say
that the length of the delay branch must almost be twice
the length of the secondary waveguide. Since the length
of the delay branch has already been chosen we have to
design the secondary waveguide. A proper structure is
for example the one whose projections on the longitudi-
nal and transversal directions are respectively equal to 35
and 2, that gives a difference of length between the in-
terested part of the main waveguide and the secondary
waveguide equal to 0.0571, that is less than one half of
the relative difference of length of the delay branch.
We have now to find the value of the wavevector that
allows to obtain the chosen phase values. A good values
is =30, that gives a phase value of 1.24  for the delay
branch and a phase value of 0.55  (a bit larger than the
minimum value of /2 that allows the Repulsion between
two close soliton beams) for the secon dary waveguide.
Once chosen all the geometrical values of the structure
it is necessary to select the refractive index of the
waveguides to ensure the correct trapping of the beams
inside them.
From (11) we ha ve:
022 G
D
db
naC

 (22)
Substituting the numerical values we have
5
0110
G
n

 .
Since for the seco n dary wavegui de we ha ve [13]:

F. GARZIA ET AL.
241

1
2
0
v
2
G
D
S
C
n


(23)
where is the tangent of the angle between the
waveguide and the long itudinal direction, it is possible to
solve (23) with respect to giving:
vG
0S
n
1
2
0v
2G
SD
nC




(24)
Substituting the numerical values we have
6
02.04 10 S
n , that is 5 times less than the value
found for the delay branch. This difference reflects the
different geometry, and therefore the different propaga-
tion conditions, of the two considered optical structures.
We further choose for the main waveguide a refractive
index value equal 5
0110
G
n

 , so that the beam that
propagates inside the main waveguide does not enter in
the delay branch unless it is pushed inside it.
The design appro ach used until this point is obviously
practical for the numerical simulations since, as we al-
ready said, we have no physical restrictions, but abso-
lutely impossible to be used in a real device design due
to the greater number of limitations that is necessary to
respect. We show a real design approach in the follow-
ing.
Further we neglect to insert at the end of the structure
a proper propagation distance that allows to the beam
that enters alone in the structure through input 1 to exit
with the same input phase, since we are mainly interested
to the phase variations. The drain waveguide has been
designed in a way similar to the seco ndary waveguide.
The geometry of the designed structure is shown in
Figure 6(a).
Let us analyse the results of the numerical simulations
for the three possible input combinations to demonstrate
the correctness of the developed theory, neglecting the
situation of no inputs that represents the first combina-
tion according to Table 1.
In Figure 6(b) the numerical simulation in case of the
presence of the only input pulse at the entrance 1 (the
second input combination of Table 1) is shown. In this
case, since the refractive index variation is equal to the
one of the delay branch, the beam propagates undis-
turbed and reaches the output, generating a proper phase
coded pulse.
In Figure 6(c) the numerical simulation of the third
input combination, that is the presence of only an input
pulse at the entrance 2 is shown. In this case, the pulse
first propagates properly trapped inside the secondary
waveguide, due to the fact that the parameters of the
structures have been designed to lock it. It reaches the
main waveguide, with a certain phase difference that we
have designed to be equal to 0.55 , reaching the output,
and generating a proper output phase coded pulse.
In Figure 6(d) the numerical simulation of the fourth
input combination, that is the presence of both input
pulses at the entrances is shown. In this case, the two
pulses meet at the merging point between the main
waveguide and the secondary waveguide with a relative
phase difference greater than 0.55 , that is in a repulsive
situation. The two beams propagate parallel each other
properly separated, until reaching the bifurcation point.
In this zone the pulse relative to input 1 is pushed into
the delay branch, while the pulse relative to input two is
pushed inside the drain waveguide where it reaches the
drain output. The first pulse, that propagates inside the
delay branch, is trapped inside it since the structure has
been properly designed and enters again inside the main
waveguide with a relative designed phase difference
equal to 1.24 , reaching the output and generating a
proper outp ut phase coded pulse.
The numerical simulations, as shown in Figures 6,
confirm the theory developed.
5. A Numerical Design of the Device
We want now to give a numerical example for the design
(a)
(b)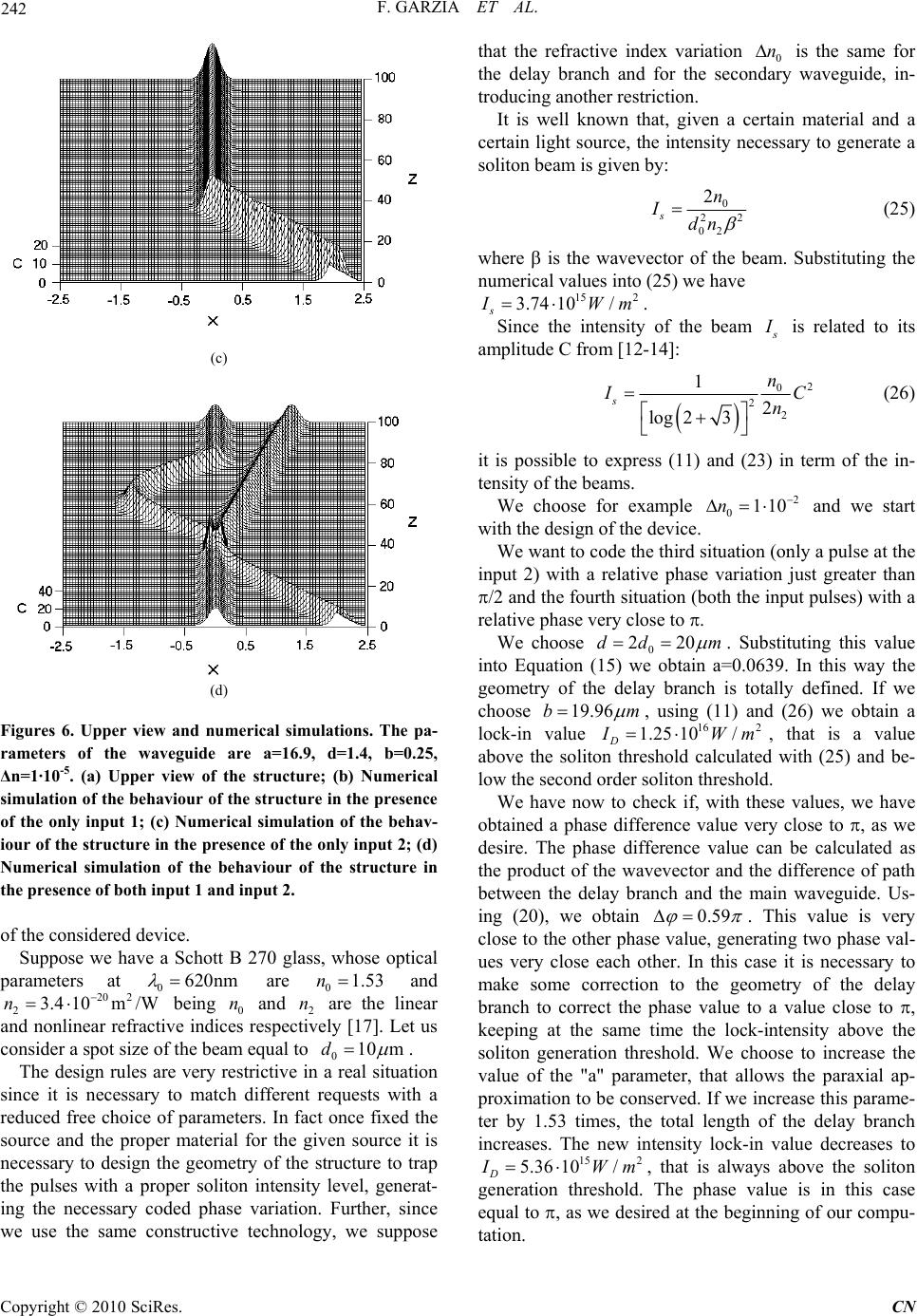

242 F. GARZIA ET AL.
(c)
(d)
Figures 6. Upper view and numerical simulations. The pa-
rameters of the waveguide are a=16.9, d=1.4, b=0.25,
Δn=1·10-5. (a) Upper view of the structure; (b) Numerical
simulation of the behaviour of the structure in the presence
of the only input 1; (c) Numerical simulation of the behav-
iour of the structure in the presence of the only input 2; (d)
Numerical simulation of the behaviour of the structure in
the presence of both input 1 and input 2.
of the considered device.
Suppose we have a Schott B 270 glass, whose optical
parameters at 0620nm


/W n are 0 and being 0 and 2 are the linear
and nonlinear refractive indices respectively [17]. Let us
consider a spot size of the beam equal to
1.53n
10d
20 2
23.4 10mn
 n
0m

.
The design rules are very restrictive in a real situation
since it is necessary to match different requests with a
reduced free choice of parameters. In fact once fixed the
source and the proper material for the given source it is
necessary to design the geometry of the structure to trap
the pulses with a proper soliton intensity level, generat-
ing the necessary coded phase variation. Further, since
we use the same constructive technology, we suppose
that the refractive index variation 0 is the same for
the delay branch and for the secondary waveguide, in-
troducing another restriction.
n
It is well known that, given a certain material and a
certain light source, the intensity necessary to generate a
soliton beam is given by:
0
22
02
2
s
n
Idn

 (25)
where  is the wavevector of the beam. Substituting the
numerical values into (25) we have
15 2
3.74 10/
s
I
Wm .
Since the intensity of the beam
s
I
is related to its
amplitude C from [12-14]:

2
0
22
1
2
log 23
s
n
I
C
n



(26)
it is possible to express (11) and (23) in term of the in-
tensity of the beams.
We choose for example and we start
with the design of the device.
2
0110n

We want to code the third situation (only a pu lse at the
input 2) with a relative phase variation just greater than
/2 and the fourth situation (both the input pulses) with a
relative phase very close to .
We choose 0 220dd m



.96 m
. Substituting this value
into Equation (15) we obtain a=0.0639. In this way the
geometry of the delay branch is totally defined. If we
choose 19b


, using (11) and (26) we obtain a
lock-in value 16
1.25 10
D2
/
I
Wm , that is a value
above the soliton threshold calculated with (25) and be-
low the second order soliton threshold.
We have now to check if, with these values, we have
obtained a phase difference value very close to , as we
desire. The phase difference value can be calculated as
the product of the wavevector and the difference of path
between the delay branch and the main waveguide. Us-
ing (20), we obtain 0.59



. This value is very
close to the other phase value, generating two phase val-
ues very close each other. In this case it is necessary to
make some correction to the geometry of the delay
branch to correct the phase value to a value close to ,
keeping at the same time the lock-intensity above the
soliton generation threshold. We choose to increase the
value of the "a" parameter, that allows the paraxial ap-
proximation to be conserved. If we increase this parame-
ter by 1.53 times, the total length of the delay branch
increases. The new intensity lock-in value decreases to
15 2
5.3610/
D
I
Wm , that is always above the soliton
generation threshold. The phase value is in this case
equal to , as we desired at the beginning of our compu-
tation.

F. GARZIA ET AL.
243
It is now necessary to project the secondary input
waveguide. We want to obtain the same inten sity lock-in
value calculated for the delay branch and a phase differ-
ence value a bit greater than /2.
This kind of waveguide as already been studied [13]
showing a behaviour similar to the parabolic waveguide
and a lock-in value equal to:

1
2
0
v
2
G
D
C
n


(27)
where is the tangent of the inclination angle with
respect to the longitudinal direction. It is obviously nec-
essary to respect, even in this case, the paraxial approxi-
mation; this means that once we have chosen the distance
vG
L
a between the second input and the main input, the
longitudinal length
L
b of the waveguide cannot be
shorter than a minimum, calculated according to the
paraxial limit, that is:
tan80.14
L
L
ab b
L
(28)
Since we suppose to generate this waveguide using the
same physical procedure used for the delay branch, we
have to suppose that the value is th e same
for both the waveguides. If we use as a first attempt
value L, to generate a device whose lateral exten-
sions with respect to the main waveguide are the same,
we immeditely obtain
2
0110n

ad
a
L
b from (28), that allows us to
calculate . Substituting these values into (27), using
(26) we have an intensity lock-in value equal to
G
v
2.23 1017 2 /
DS
I
Wm and 1.12
S




d
. The wave-
guide designed according to these criteria is totally use-
less for our purpose since the lock-in value is greatly
above the generation value of a second order soliton and
consequently above the lock-in value calculated for the
delay branch. Further, the phase value obtained is totally
different with respect to the one we desire. It is therefore
necessary to find another approach. If we impose the
waveguide to have the same lock-in intensity of the delay
branch, considering always L
a, we can calculate
L
b5650b , reversing the reasoning followed above. In this case
we obtain Lm

 that satisfies the paraxial con-
dition expressed by (27). If we calculate the phase dif-
ference we have S0.175

  , that is not only a dif-
ferent value with respect to the desired one but also a
value that does not allow the repulsion between the two
beams, that is a fundamental condition to make the de-
vice operate correctly.
Consequently it is necessary to act also on
L
a, con-
sidering a device that has not the same lateral extension
with respect to the main waveguide. Fixing the intensity
lock-in level to be equal to the one of the delay branch
and fixing the phase difference S

 to be as close as
possible to 0.5 , it is possible to demonstrate that a valid
waveguide is the one characterised by 360
L
ad m


and 16935
L
bm


, that provides a phase difference
S0.53



, respecting the paraxial condition ex-
pressed by (27).
The problems found in the design of the secondary
input waveguide could be avoided if we could act also on
0
n

, but this is very difficult to be made in a real situa-
tion where both the delay branch and the inclined
waveguide are generated in the same process.
Different approaches can be used to design the device,
as for example, to dimension first the secondary wave-
guide and the delay branch, but they are always sub-
jected to different restrictions due to the physics of the
waveguides generation process.
6. Temporal Considerations
Further considerations about the temporal behaviour and
the absorbing behaviour of solitons in transverse refrac-
tive index profile device have already been studied
[13,14] and they are not repeated here for brevity.
Since the response time of the considered material are
of the order of femtoseconds, the proposed device can
reach operative velocity of the order of thousands of
Gbit/s and it is limited o nly by the operative v elocities of
the actual sources.
7. Conclusions
We have studied and designed an all-optical crypto-
graphic device, whose working principles are based on
the repulsive and propagation properties of solitons in a
parabolic transverse refractive index profile, that we
deeply analysed in the paper.
The switching properties have been studied in details,
obtaining some useful design criteria for a practical de-
vice.
The device can be properly designed by means of the
geometrical and optical parameters of the different
structures that compose the modulator.
Due to its peculiar features, the only limit to its maxi-
mum operative velocity is represented by the maximum
repetition rate of the input sour ces.
8. References
[1] R. Y. Ciao, E. Garmire and C. H. Townes,
“Self-Trapping of Optical Beams,” Physical Review
Letters, Vol. 13, No. 15, 1964, pp. 479-482.
[2] B. Luther-Davies and Y. Xiaoping, “Waveguides
and Y Junctions Formed in Self-Defocusing Dark
Spatial Soliton,” Optics Letters, Vol. 17, No. 7,
1992, pp. 496-498.

244 F. GARZIA ET AL.
[3] W. Krolikowski and Y. S. Kivshar, “Soliton-Based
Optical Switching In Waveguide Arrays,” Journal
of the Optical Society of America B, Vol. 13, No. 5,
1996, pp. 876-887.
[4] N. N. Akhmediev and A. Ankiewicz, “Spatial
Soliton X-Junctions and Couplers,” Optics
Communications, Vol. 100, No. 1-4, 1993, pp.
186-192.
[5] W. Krolikowski, X. Yang, B. Luther-Davies and J.
Breslin, “Dark Soliton Steering in a Saturable
Nonlinear Medium,” Optics Communications, Vol.
105, No. 3-4, 1994, pp. 219-225.
[6] A. P. Sheppard, “Devices Written by Colliding
Spatial Solitons: A Coupled Mode Theory
Approach,” Optics Communications, Vol. 102, No.
3-4, 1993, pp. 317-323.
[7] J. P. Gordon, “Interaction Forces among Solitons in
Optical Fibers,” Optics Letters, Vol. 8, No. 11,
1983, pp. 596-598.
[8] F. Garzia, C. Sibilia, M. Bertolotti, R. Horak and J.
Bajer, “Phase Properties of a Two-Soliton System
in a Non Linear Planar Waveguide,” Optics
Communications, Vol. 108, No. 1-3, 1994, pp. 47-
54.
[9] A. B. Aceves, J. V. Moloney and A. C. Newell,
“Reflection and Transmission of Self-Focused
Channels at Nonlinear Dielectric Interfaces,” Optics
Letters, Vol. 13, No. 11, 1988, pp. 1002-1004.
[10] P. Varatharajah, A. B. Aceves and J. V. Moloney,
“All-Optical Spatial Scanner,” Applied Physics
Letters, Vol. 54, 1989, pp. 2631-2633.
[11] A .B. Aceves, et al., “Particle Aspects of
Collimated Light Channel Propagation at Nonlinear
Interfaces and in Waveguides,” Journal of the
Optical Society of America B, Vol. 7, No. 6, 1990,
pp. 963-974.
[12] F. Garzia, C. Sibilia and M. Bertolotti, “Swing
Effect of Spatial Soliton,” Optics Communications,
Vol. 139, No. 4-6, 1997, pp. 193-198.
[13] F. Garzia, C. Sibilia and M. Bertolotti, “High Pass
Soliton Filter,” Optics Communications, Vol. 152,
No. 1-3, 1998, pp. 153-160.
[14] F. Garzia, C. Sibilia, and M. Bertolotti, “All optical
soliton based router”, Opt. Comm., vol. 168/1-4, pp.
277-285, 1999.
[15] H. W. Chen and T. Liu, “Nonlinear Wave and
Soliton Propagation in Media with Arbitrary
Inhomogeneities,” Physics of Fluids, Vol. 21, No. 3,
1978, pp. 377-380.
[16] P. K. Cow, N. L. Tsintsadze and D. D. Tsakhaya,
“Emission of Ion-Sound Waves by a Langmuir
Soliton Moving with Acceleration,” Soviet
Physics-JETP, Vol. 55, 1982, pp. 839- 843.
[17] J. S. Aitchison, et al., “Observation of Spatial
Optical Solitons in a Nonlinear Glass Waveguide,”
Optics Letters, Vol. 15, No. 9, 1990, pp. 471-473.
[18] P. Refreiger and B. Javidi, “Optical Image
Encryption on Input Plane and Fourier Plane
Random Encoding,” Optics Letters, Vol. 20, No. 7,
1995, pp.767-769.
[19] O. Matoba and B. Javidi, “Encrypted Optical
Memory System Using Three-Dimensional Key in
the Fresnel Domain,” Optics Letters, Vol. 24, No.
11, 1999, pp.762-764.
[20] J. W. Han, C. S. Park, D. H. Ryu and E. S. Kin,
“Optical Image Encryption Based on XOR
Operations,” Optical Engineering (Bellingham),
Vol. 38, No. 1, 1999, pp. 47-54.
[21] J. W. Han, S. H. Lee and E. S. Kin, “Optical Key
Bit Stream Generator,” Optical Engineering
(Bellingham), Vol. 38, No. 1, 1999, pp. 33-38.
[22] S. T. Liu, Q. L. Mi and B. H. Zhu, “Optical Image
Encryption with Multistage and Multichannel
Fractional Fourier-Domain Filtering,” Optics
Letters, Vol. 26, No. 16, 2001, pp. 1242-1244.
[23] Y. Zhang, C. H. Zheng and N. Tanno, “Optical
Encryption Based on Iterative Fractional Fourier
Transform,” Optics Communications, Vol. 202, No.
4-6, 2002, pp. 277-285.
[24] A. Carciner, M. Montes-Usategui, S. Arcos and I.
Juvells, “Vulnerability to Chosen-Cyphertext
Attacks of Optical Encryption Schemes Based on
Double Random Phase Keys,” Optics Letters, Vol.
30, No. 13, 2005, pp. 1644-1646.
[25] U. Gopinathan, D. S. Monaghan, T. J. Naughton
and J. T. Sheridan, “A Known-Plaintext Heuristic
Attack on the Fourier Plane Encryption Algorithm,”
Optics Express, Vol. 14, No. 8, 2006, pp.
3181-3186.
[26] Y. Frauel, A. Castro, T. J. Naughton and B. Javidi,
“Resistance of the Double Phase Encryption against
Various Attacks,” Optics Express, Vol. 15, No. 16,
2007, pp. 10253-10265.
[27] P. K. Wang, L. A. Watson and C. Chatwin,
“Random Phase Encoding for Optical Security,”
Optical Engineering (Bellingham), Vol. 35, No. 9,
1996, pp. 2464-2469.
[28] Y. Li, K. Kreske and J. Rosen, “Security and
Encryption Optical Systems Based on a Correlator
with Significant Output Images,” Applied Optics,
Vol. 39, No. 29, 2000, pp. 5925-5301.
[29] Z. J. Liu and S. T. Liu, “Double Image Encryption
Based on Iterative Fractional Fourier Transform,”
Optics Communications, Vol. 275, No. 2, 2007, pp.
324-329.
[30] B. Javidi and T. Nomura, “Securing Information by
Use of Digital Olography,” Optics Letters, Vol. 25,
No. 1, 2000, pp. 28-30.
[31] N. K. Nischal, J. Joseph and K. Singh, “Securing
Information Using Fractional Fourier Transform in
Digital Olography,” Optics Communications, Vol.
235, No. 4-6, 2004, pp. 253-259.

F. GARZIA ET AL.
245
[32] X. F. Meng, X. Peng, L. Z. Cai, A. M. Li, Z. Gao
and Y. R. Wang, “Cryptosystem Based on Two
Step Phase-Shifting Interferometry and the RSA
Pubblic-Key Encryption Algorithm,” Journal of
Optics A: Pure Applied Optics, Vol. 11, No. 8,
2009, pp. 85402-85410.
[33] Y. Zhang and B. Wang, “Optical Image Encryption
Based on Interference,” Optics Express, Vol. 33,
No. 21, 2008, pp. 2443-2445.