Paper Menu >>
Journal Menu >>
 Journal of Signal and Information Processing, 20 10 , 1, 63 -76 doi:10.4236/jsip.2010.11007 Published Online November 2010 (http://www.SciRP.org/journal/jsip) Copyright © 2010 SciRes. JSIP 63 A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Nandini Basumallick, S. V. Narasimhan Aerospace Electronics and Systems Division, National Aerospace Laboratories, Council of Scientific and Industrial Research (CSIR), Bangalore, India. Email: narasim@nal.res.in Received October 29th, 2010; revised November 13th, 2010; accepted November 15th, 2010. ABSTRACT A new adaptive Packet algorithm based on Discrete Cosine harmonic wavelet transform (DCHWT), (DCAHWP) has been proposed. This is realized by the Discrete Cosine Harmonic Wavelet transform (DCHTWT) which exploits the good properties of DCT viz., energy compaction (low leakag e), frequency resolution and computational simplicity due its real nature, compared to those of DFT and its harmonic wavelet version. Hence the proposed wavelet packet is ad- vantageous both in terms of performance and computational efficiency compared to those of existing DFT harmonic wavelet packet. Further, the new DCAHWP also enjoys the desirable properties of a Harmonic wavelet transform over the time domain WT, viz., built in decimation without any explicit antialiasing filtering and easy interpolation by mere concatenation of differen t scales in frequency (DCT) domain with out any image rejection filter and with out laborious delay compensa tion required. Further, the compression by the proposed DCAHWP is much better compared to that by adaptive WP based on Daubechies-2 wavelet (DBAWP). For a compression factor (CF) of 1/8, the ratio of the per- centage error energy by proposed DCAHWP to that by DBAWP is about 1/8 and 1/5 for considered 1-D signal and speech signal, respectively. Its compression performance is better than that of DCHWT, both for 1-D and 2-D signals. The improvement is more significant for signals with abrupt changes or images with rapid variations (textures). For compression factor of 1/8, the ratio of the percentage error energy by DCAHWP to that by DCHWT, is about 1/3 and 1/2, for the considered 1-D signal and speech signal, respectively. This factor for an image considered is 2/3 and in particular for a textural image it is 1/5. Keywords: Adaptive Harmonic Wavelet Packets, Discrete Cosine Transform, Signal Compression 1. Introduction The wavelet transform (WT) provides a frequency de- pendent resolution so that the high and low frequencies have a coarse and fine frequency resolution. This is based on the assumption that high and low frequencies require, fine time resolution and coarse frequency resolu - tion; respectively. But to achieve for high frequencies, a finer frequency resolution and for low frequencies, a finer time resolution; the wavelet packet (WP) system is used [1]. It also allows flexibility of selection of wavelet tree structure that enables the WP to select an optimum time-frequency tiling for a given data. This is achieved by adaptive WP and compared to the normal WT, it is more attractive, for applications like signal compression and transient detection [2-5]. This is because the adaptive nature of WP facilitates better energy compaction. Basically, the WP is a generalization of the WT. In WT, only the coarse/approximation is split at each stage and the detail is carried down as it is. Unlike this, in WP at each stage, the detail/highpass filter branch is also fur- ther split and decimated similar to the approximation/ lowpass branch. Thus the complexity of the WP algo- rithm is more as compared to that of the conventional WT. Hence filterbank realization of WP is cumbersome as it involves additional filtering and sampling rate con- version. To simplify the adaptive WP, a Harmonic Wavelet Packet based on Discrete Four ier Transform (DFAHW P)  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 64 has been used [4]. This is possible as the Harmonic WT (HWT) due to its built in decimation and interpolation and absence of any explicit antialiasing and image rejec- tion filtering. However for such a HWT, its coefficients not only suffer from leakage effect but also are of com- plex nature. Further for an image (2D signal), the HWT complex nature involves approximation which results in neglection of the imaginary part of a coefficient once along the rows and columns during each LL stage split- ting [9]. These drawbacks are carried over to the DFAHWP also. To overcome these limitations, a HWT based on Discrete Cosine Transform (DCHWT) has been used [8,9]. This is based on the fact that DCT provides real coefficients, which are also less affected by leakage [8,12]. The DCHWT has been used for computationally efficient and better quality signal compression and sub- band spectral estimation [9]. This has also been applied for reducing the cross-term effect, which occurs in Wigner-Ville distribution [10]. Further, a shift invariant version of DCHWT has been considered for applications like signal denoising which reduc es glitches in th e recon- structed signals [11]. In this paper, an adaptive Harmonic Wavelet Packet based on DCT (DCAHWP) is proposed. The method is computationally simple, as it is based on grouping of real DCT coefficients and the WP decomposition up to the last level is readily available in DCT domain with out any repeated filtering and decimation like in a time domain filter bank. Further, the reconstruction also does not in- volve any explicit interpolation and its associated filter- ing. The new algorithm has a better performance than the DFAHWP as its scales are less affected by leakage effect and does not involve any approximation for 2D signals. The DCAHWP has been applied both for 1-D and 2-D signal compression and its performance is better com- pared to that of DCHWT. Further its performance is su- perior to that of DBAWP for 1D signals. 2. Adaptive Wavelet Packet The WP decomposition for a signal, showing the split of detail/ highpass branch in addition to coarse/lowpass branch, is illustrated in Figure 1(a). For a signal of Npoints, this generates an array of M N coefficients where M is the total number of decomposition stages, given by 2 log M N . From this array, N coefficients can be selected to represent the signal. These N coeffi- cients can be that of normal WT decomposition or any other combination. Wavelet packet facilitates selection of an optimal basis for a given signal. In an adaptive wavelet packet, a spe- cific combination of all the branches is selected to repre- sent a particular signal based on some predefined crite- rion. The criterion generally aims at having maximum infor mat ion wi th min imu m po ssib le nu mber of coef fic ien ts.  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 65 Figure 1. (a) Wavelet packet showing the split of detail/high pass branch in addition to coarse/lowpass branch (b) Optimum scale tree selection, (c) Optimum scale tree. That is, it minimizes the number of nonzero coef ficients of the resulting wavelet transform. The criterion or cost function used in practice is the Shannon’s entropymeas- ure, give n by 1 0log L ii i Epp p , (1) ( log 0 ii pp if0 i p) where Ep is the entropy for a particular scale, and L is the number of wavelet packet coefficients in that scale. i p are the normalized energies of the wavelet packet coefficients to be considered and are given by [4] 2 2 i i x p s , 1 22 0 () N n s sn (2) where, i x are the absolute values of wavelet packet coefficients in that scale, 2 s is the normalization fac- tor and s n is the original signal of length N. Let H be the Hilbert space, vHand i H H be an orthogonal decomposition of H . The entropy of v relative to the decomposition i H of H is defined [3,6] as a measure of the distance between v and the orthogonal decomposi t i on. 22 2;ln iii vHv v 2 is characterized by the Shannon equation. If ij H HHHH , i H and j H give the orthogonal decompo sitions i H H and j H H . Then the Shannon entropy is given by 2222 22222 ; ,lnln ij i vvvv vHH vvv v 22 22 ;; ij vv vHvH vv This equation enables searching for the smallest en- tropy expansion of a signal. The best basis algorithm minimizes the cost function for the transform coefficients. This involves complete decomposition according to the wavelet packet transform. For the wavelet packet decomposition of a signal shown in Figure 1a, the entropies for different scales are as given below: The entropy for scale0 A , 000 0 22 1 22 0.log Aii LAA Ai xx Ess The entropy for scale1 A , 111 1 22 1 22 0.log A LAj Aj Aj xx Ess , And the entropy for scale A A, 22 1 22 0.log AA LAAk AAk AA k xx Ess . Here 0 Ai x ,1 Aj x and AAk x are the wavelet packet coefficients in the scales 0 A ,1 A and A A, having 0A L, 1A L and AA L samples; respectively. The entropies of other scales can also be found in a similar manner. The entropy will be low when energy is concentrated only at few locations, furth er it will be zero only when all the energy of the signal is at one coefficient. On the other  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 66 hand, the entropy will be maximum when energy is equally distributed over all coefficients. Hence the set of N wavelet packet coefficients for which en trop y is least provides the efficient representation of the signal. This enables to select those coefficients set which has maxi- mum concentration of the energy. To choose such a set, at each scale, each pair of parti- tioned coefficient sets is compared with those of their parent from which the partitions are derived. If the com- bined partition coefficients have entropy smaller than that of their parent, the partitions are considered, other- wise the parent.To make further comparisons while pro- ceeding upwards (towards parent), if partitions are con- sidered, then their entropy is assigned to their parent. In this way the complete wave packet array is scanned and this provides an optimal time-frequ ency tiling in terms of location of coefficient energy. The Figure 1b shows the method of optimum splitting for an arbitrary case. Here, the combined entropy of S and A is less than the signal spectrum entropy. Hence, this signal spectrum splitting into S and A is valid. Further for S, its splitting into SS and SA is not valid as the combined entropy of SS and SA is greater than that of S. But splitting of A into A S and A A is valid as their combined entropy is less than that of A . Further, split of A S into 3 A and 2 A is not valid as their combined entropy is larger than that of A S. But A A split into 1 A and 0 A is valid as their combined entropy is less than that of A A. The optimum scale tree selected is shown in the Figure 1c. The decimation of the scales in the scale tree selected depends up on the bandwidth of the individual scales resulting in a time-frequency tiling and this may totally differ from the normal dyadic tiling. Such a tiling results in a maximum energy compaction for a given number of coefficients. It is not only the time frequency tiling but also the wavelet function used, also determines the per- formance of compression. That is, a good wavelet for a particular signal results in a good energy compaction with least number of coefficients. Thus the wavelet packet can result in an efficient lossless compression. This type of scale tree selection is also known as best basis selection. 3. Discrete Cosine Harmonic Wavelet Transform The filter bank realizatio n of WT, invo lves decimation of the scale components. The restoration of the processed overall spectrum corresponding to the original sampling rate, involves interpolation and summation of the inter- polated scale outputs in time. The harmonic wavelet transform based on DFT (DFHWT) realizes the subband decomposition in the frequency domain by grouping the Fourier transform (FT) coefficients and the inverse of these groups results in decimated signals [7]. Further after processing, the FT of the scales can be repositioned in their corresponding positions to recover the overall spectrum, with the original sampling rate. Therefore, this will not involve explicit decimation and interpolation operations. As a consequence, no band limiting and im- age rejection filters are necessary. Also, while recon- struction, there are no delay compensations as the scales are combined in the frequency domain by repositioning them. In view of this, the harmonic subband decomposi- tion is very attractive due to its simplicity. Further, the decomposition being done in frequency domain, it is well suited for those processing methods which are performed in frequency domain, like group delay processing [8 ]. For a 1-D signal in the DFHWT, the grouping of the DFT coefficients with possible conjugate symmetry though makes the WT coefficients complex; this will not pose any problem for reconstruction as after concatena- tion of the groups, the conjugate symmetry is restored to get the real signal. The DFHWT is very attractive as long as no process- ing of the components is involved prior to inverse trans- formation. However, for a signal segment obtained without using any window fun ctio n, ther e can be a seve re leakage effect from one scale to another scale. If differ- ent scales have to be processed differently, this is not achieved as the signal energy from one to another has already leaked. The DFHWT may be tolerable for a sig- nal with well-separated frequency components of suffi- ciently high magnitude. But for closely spaced compo- nents of significantly different magnitudes, during the computation of the FT itself, the energy will leak from the higher amplitude component to the lower one (and vice versa). This results in a large bias in the spectral magnitude and may even totally eclipse smaller ampli- tude spectral peaks. In such a case, decomposing the signal based on DFHWT and processing the subbands may not be very effective. Further leakage in DFHWT will also limit its use in signal or image compression application. The reason for this is that it is not p ossible to get a good signal reconstruction by omitting the lower scales (corresponding to high frequencies) in WT as the leaked energy cannot be recovered unless all the scales are considered Therefore to utilize the attractive features of the har- monic wavelet transform, DCT is used instead of DFT, which has a comparatively reduced leakage effect. This is due to symmetrical data extension which results in a smooth transition from one DCT period to the other without any discontinuity [8]. The wavelet transform , x Wabcharacterizes the cor-  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 67 relation or similarity between the signal x tto be ana- lyzed and the wavelet function /tba . Such a correlation is given by * 1/2 1 , xtb Wab xtdt a a (3) where t is the prototype/mother wavelet. By shifting and scaling t by the parameters b and a, respec- tively; all the basis funct ions 1/2 ,ab ta tba are obtained. Eqn. (3) can be realized in the frequency domain using Parseval’s theorem as [13] 1/2 * ,2 jb xa WabXa ed (4a) Therefore, the wavelet transform can be derived by windowing the spectrum X with *a and inverse Fourier transforming the product. 1/2 1* , x Wab aFXa (4b) and X are the FT of the mother wave- let t and the signal x t. That is, , x Wab for a particular scale ''a can be computed by the Eqn. (4b) using X and a by FFT algorithm. For a real symmetric signal s x t and a real sym- metric wavelet st function, Eqn.(2a) becomes [9] 1/2 ,cos 2 xss a CabX a bd (5a) s X and s are the Fourier transfo rm of s x t and st respectively. (Generally the wavelet function is a symmetrical one but to have con sistency in the nota- tion st is used). In other words, they are the cosine transforms of s x t and the mother wavelet st . , x Cab is the wavelet transform in cosine domain in- stead of Fourier domain. Hence the corresponding equa- tion for Eqn.(4b) is 1/2 1 , xss CabaC Xa (5b) Therefore the cosine wavelet transform coefficient , x Cabfor a particular scale ''a can be computed by the Eqn. (5b) using s X and sa by a fast cosine transform algorithm which indirectly uses FFT algorithm. s is very simple for the Harmonic cosine wavelet transform (CHWT), and it is zero at all frequencies except constant over a small frequency band. 00 00 1, , () , 0, cc scc otherwise (5c) For this the wavelet)(t s is, 0 sin cos cc sc t tt t Representing sin c c t t by sin c ct , 0 cos sin c sc ttct (5d) Hence the mother wavelet is a cosine modulated sinc function. Here the decomposition of the signal in the frequency domain is simple but suffers from the problem of poor time localization due to slow decaying of the sinc function. Though a spectral weighing other than rectan- gular improves the localization in time it results in a non-orthogonal wavelet set. The type of spectral weigh- ing will determine the wavelet as it is the cosine trans- form of the wavelet. For the cosine harmonic wavelet transform, the spec- tral weighing is a symmetrical rectangular function and for a discrete signal it is zero except over symmetrical finite bands ,pq and ,pq where ,pq can be real numbers, not necessarily integers. For an orthogon al CHWT, the wavelet func tion is fixed and corresponds to a rectangular weighing in the fre- quency domain which results in such a wavelet trans- form. The Discrete cosine transform (DCT) enables the im- plementation of the above cosine transform discussed as it forms the symmetric signals s x t and st by itself (for the given non-symmetric x t and t . For a sampled signal x n, 0,1,2, 1nN, the DCT of N points, is defined as the DFT of a 2N point symmetrically extended signal y n. 12),12( 10),( )( NnNnNx Nnnx ny y nis even symmetric with respect to the point 12N . This leads to DCT and is given by 1 0 21 2cos,0 1 2 2, 21 N n x x kn xnk N Ck N CNkNkN (6) Using the above s in the CHWT, the subband decomposition is done in frequency domain unlike in time domain by a filter bank. This is achieved by group- ing the 2N coefficients of a discrete cosine transform (DCT) of length 2Nand this is equivalent to applying a window or weighing by a constant in the frequency do- main. The DCT coefficients can be grouped in a way similar to that of DFT coefficients and the DCT being r eal, there 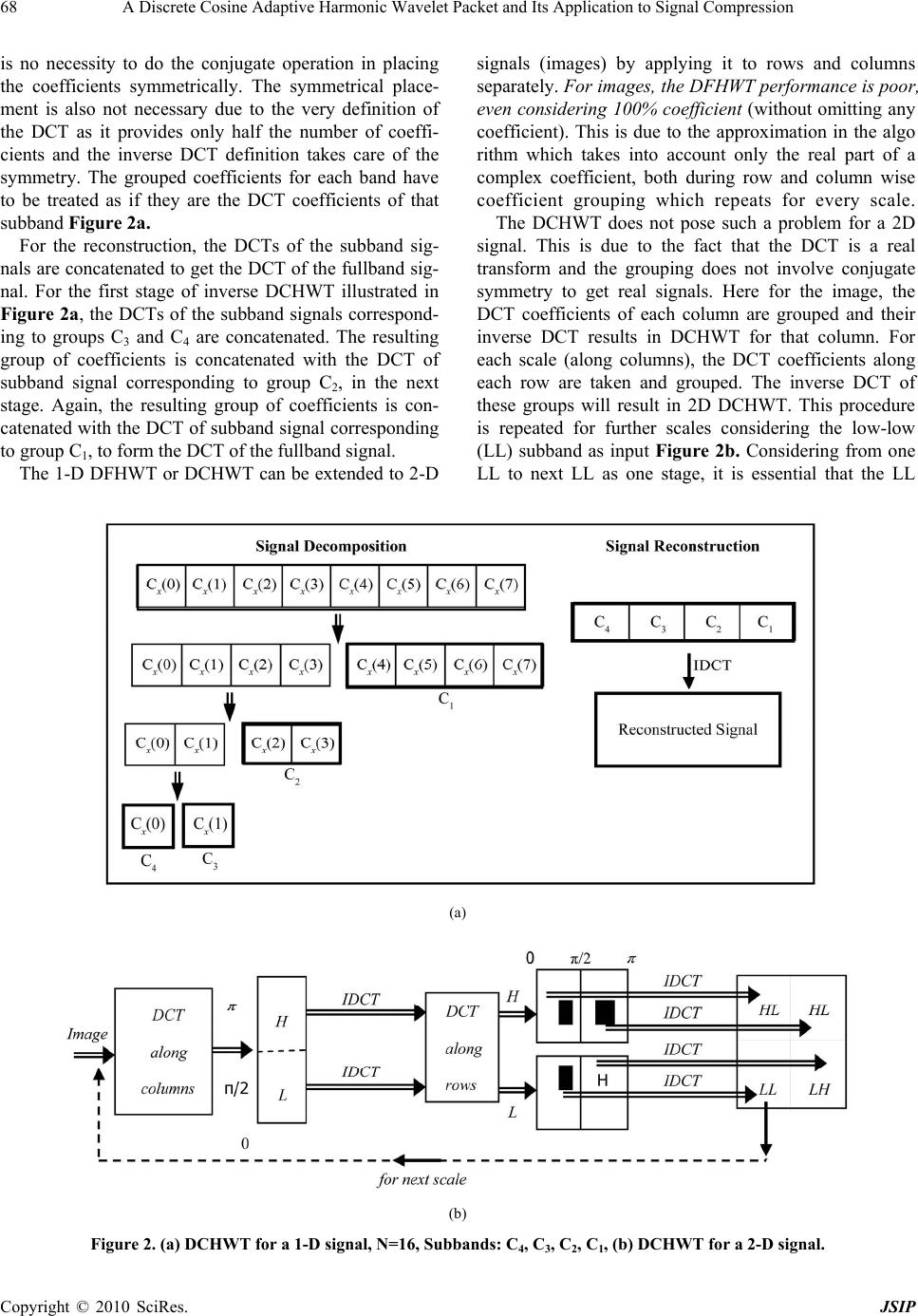 A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 68 is no necessity to do the conjugate operation in placing the coefficients symmetrically. The symmetrical place- ment is also not necessary due to the very definition of the DCT as it provides only half the number of coeffi- cients and the inverse DCT definition takes care of the symmetry. The grouped coefficients for each band have to be treated as if they are the DCT coefficients of that subband Figure 2a. For the reconstruction, the DCTs of the subband sig- nals are concatenated to get the DCT of the fullband sig- nal. For the first stage of inverse DCHWT illustrated in Figure 2a, the DCTs of the subband signals correspond- ing to groups C3 and C4 are concatenated. The resulting group of coefficients is concatenated with the DCT of subband signal corresponding to group C2, in the next stage. Again, the resulting group of coefficients is con- catenated with the DCT of subband signal corresponding to group C1, to form the DCT of the fullband signal. The 1-D DFHWT or DCHWT can be extended to 2-D signals (images) by applying it to rows and columns separately. Fo r images, the DFHWT performan ce is poor, even considering 100% coefficient (without omitting any coefficient). This is due to the approximation in the algo rithm which takes into account only the real part of a complex coefficient, both during row and column wise coefficient grouping which repeats for every scale. The DCHWT does not pose such a problem for a 2D signal. This is due to the fact that the DCT is a real transform and the grouping does not involve conjugate symmetry to get real signals. Here for the image, the DCT coefficients of each column are grouped and their inverse DCT results in DCHWT for that column. For each scale (along columns), the DCT coefficients along each row are taken and grouped. The inverse DCT of these groups will result in 2D DCHWT. This procedure is repeated for further scales considering the low-low (LL) subband as input Figure 2b. Considering from one LL to next LL as one stage, it is essential that the LL (a) (b) Figure 2. (a) DCHWT for a 1-D signal, N=16, Subbands: C4, C3, C2, C1, (b) DCHWT for a 2-D signal.  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 69 subband which goes as input should be in data domain and not in frequency (DCT) domain. This is essential as it enables to split DCT of columns in to H and L and proceed further. Since no approximations are made, there will not be any error when the image is constructed with 100% coefficients [9] wh ich is not so with DFHWT. 4. Discrete Cosine Adaptive Harmonic Wavelet Packet (DCAHWP) The DCAHWP for both 1-D and 2 -D sign als will be con- sidered in this section. 4.1 For 1-D Signal Adaptive wavelet packets can be realized in the fre- quency domain using the approach of grouping of fre- quency domain coefficients (harmonic wavelet packet) [4]. The DCT based harmonic wavelet packet is simpler because the DCT coefficients are nothing but d ecomposi- tion up to the last possible level and they are directly available withou t any filtering unlike th e discrete wa velet transform realized by a filter bank. Further compared to DFAHWP, their low leakage effect and real nature con- tribute to the quality and simplicity of DCAHWP. The DCAHWP decomposition is illustrated in Figure3. Unlike in DCHWT Figure2a, the high subband is also split into two subbands at each decomposition level, apart from the low subband like in any WP. Ev en though the decomposition up to the last level, to apply the treat- ment of adaptive WP, it is indicated in Figure 3 as if all the DCT coefficients are together and its splitting takes place as in time domain filter bank approach. Here rather levels 2 and 1 are formed by combining the coefficients available at level-3. Maintaining the total number of coefficients equal to the signal length, different combinations of subbands may be possible for reconstruction. For DCAHWP also, the scales/subbands to be used for reconstruction are selected such that their combined entropy is minimum, as described in Section-2. Here a detailed algorithm for this is given. Algorith m for DAHWP implem entation: 1) Compute the N-point Discrete cosine transform (DCT) of the N-point signal. 2) The DCT coefficients correspond to the level (last level) 2 logLN . Obtain the other 1L decompo- sitions of WP by grouping the DCT coefficients. The number of scales/subbands at level l is 2land each is of length 2 L l points; 1ltoL . 3) Starting from the last level, the sum of entropy lev- els of two adjacent subbands/scales (children) in that level, are comp ared to the entropy of the band in the pre- vious level (parent) from which they were formed (actu- ally the parent is formed from children here !). If the combined entropy of th e children is found to be less than that of the parent, the decomposition is valid. Each time the children are selected, the combined entropy of the children is assigned to their parent for subsequent com- parisons. 4) The selected scales/subbands at different levels are used to reconstruct the signal, and the total number of coefficients is N. For compression, the number of coef- ficients to be considered is decided by the compression factor (CF). The selection of these coefficients is based on their magnitude values starting from the largest [2]. For 2-D signal: The DCAHWP implementation for a 2-D signal (image) is an extension of the above method. At each decomposi- tion level, each of the subband images (LL, HL, LH and HH achieved by the block D in Figure 4) is further di- vided into four equal subbands. This is repeated till the last possible decomposition level, that is when each subband consists of only one pixel Fi gure 4. For reconstruction, t he Figure 3. DCT harmonic wavelet packet.  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 70 Figure 4. (a) Decomposition of an image into four subbands by DCHWT. (b) DCT Harmonic Wavelet Packet Decomposition for an image. combined entropy of four children is compared to that of the parent at each level and a combination with lowest entropy is selected. The detailed al gorit hm is given. Algorithm for DCAHWP implementation: 1) First take the DCT along columns and then along rows, i.e. compute the 2-D DCT of the NN pixel image. 2) Perform the WP decomposition up to the last possi- ble level, L 2 logLN. The number of scales/subbands at level l is 4l and each is of size 22 L lLl pixels; 1ltoL. The decomposition is car- ried out by grouping the DCT coefficients. 3) Starting from the last level, the entropy comparisons are made between the children and their parent and the scales/subband decomposition tree with the lowest en- tropy is selected. 4) For reconstructing the image, the selected scales / subbands with a total of NN coefficients, are used. For compression a specified number of largest coeffi- cients amongst the NN coefficients across the scales are selected. This specific number is decided by the CF. 6. Simulation Results To illustrate the performance of the proposed DCAHWP adaptive wavelet packet, four examples: 1)1-D signal, 2) a speech signal, 3) a 2-D image (512 x 512) and 4) a tex- tural image (64 x 64); are considered. Its performance is compared with that of DCHWT. For the examples 1 and 2, the performance of the proposed method is compared with those of Daubechies-2 based WT (DBWT) and its adaptive WP (DBAWP). For all examples, the perform- ance of proposed WP method is compared with that of DCHWT. Since the performance of DFHWT is inferior to that of DCHWT [7], the proposed DCAHWP has not been compared with those of DFAHWP, the WP based on DFT. The compression performance is evaluated by the index, 100% error energy error energys ignal energy Example 1 [2]: A signal of 64 samples, having a sinu- soid and a spike Figure 5, is decomposed into subbands using both DCHWT and DCAHWP. The signal was re- constructed with and without compression in both the cases. The decomposition tree structures for DCHWT and DCAHWP are depicted in Figures 6(a), 6(b) respec- tively. Figure 5. 1-D signal having a sinusoid and a spike.  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 71 Figure 6. Decomposition tree for the signal in Figure 5 by: (a) DCHWT (b) DCAHWP. The frequency band splittin g in each decompositio n level is indicated by vertical lines. The selected groups are represented by shaded blocks. In DCHWT, the high sub- band is selected at each level and in the last level the low subband is also selected Figure 6a. But the tree structure for DCAHWP Figure 6b differs from that of DCHWT and depends on the signal characteristics The DCHWT time-frequency tiling is such that lower scales have larger frequency spacing and smaller time spacing, whereas higher scales have smaller frequency spacing and larger time spacing Figure 7a. But the DCAHWP time-frequency tiling Figure 7b is according to the best basis selected for the signal on hand. In the Figures 7a, 7b, larger coefficients are represented by darker shades. The WP coefficient values at various decomposition levels are shown in Figure 8a. At each decomposition level, each subband is further split into two subbands. For example for the level 2, Figure 8a shows the WP coefficients for the four scales; the different scales are put side by side. The same is valid for other levels also. The selected coefficients for DCHW T and D CAHW P are shown in Figures. 8b, 8c respectively. For DCHWT, a fixed set of the coefficients is selected; whereas for DCAHWP, the set of coefficients varies according to the signal. For DCAHWP the frequency band splitting is denser, providing higher frequency resolution in the low frequency range (Figure 8b). This is also found in the time-frequency plot (Figure 7b) and the tree structure (Figure 6b) for DCAHWP. However, this is not so for DCHWT (Figures. 6a, 7a, 8a). For compression, only 8 largest coefficients from the selected 64 Figure 8(b, c), are used to reconstruct the signal. Signal compression performance of DCAHWP was compared to that of DCHWT and also with that of DBWT and DBAWP. The reconstructed signal by DCAHWP with CF=1/8, contains a well defined spike in the same position as in the original (Figure 9d). But for the same CF, the spike is not clear in the reconstructed signal by DCHWT (Figure 9c). The performance of DBAWP is poor and that of DBWT is even poorer, as neither the spike nor the sinusoid are clearly brought out (Figure. 9a, b). The error plots corresponding to Figure 9(a-d) are shown in Figure 9(e-h) and it is seen that the magnitude of the error for compression by DCAHWP is significantly less than that by other methods. Further, the percentage error energy by DCAHWP is about 1/3rd of that by DCHWT and about 1/8th that of DBAWP Table 1. Example 2: For a speech signal (Figure 10) also, the results ob- tained are similar to those for example-1. For the com- pression factor 1/8, the performance of DBWT and of DBAWP are inferior compared to that of DCHWT. Be- tween DBAWP and DBWT, the former is better as is optimal for the Daubechies-2 wavelet. But DCAHWP resulted in best performance compression compared to the other methods, which is clear from comparing the reconstruction errors for the various methods (Figure 11e-h). The percentage error energy by DCAHWP is about 1/5th of that by DBAWP and about 1/2 of that by DCHWT Table 2. Table 1. % error energy (% EE) for reconstruction of the signal in Fig 5 with 1/8 coefficients (CF= 1/8). Method % EE with CF=1/8 DBWT 13.4947 DBAWP 5.8149 DCHWT 1.9550 DCAHWP 0.7396  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 72 x igure 7. Time-freque nc y tiling for the signal in Figure 5 by: (a) DCHWT (b) DCAHWP. Figure 8. WP decomposition coefficients for the signal in Figure 5. Table 2. % error energy (% EE) for reconstruction of the speech in Figure 10 with 1/8 coefficients (CF= 1/8). Method % EE with CF= 1/8 DBWT 4.2695 DBAWP 2.7425 DCHWT 1.1542 DCAHWP 0.5886 Example – 3: The performances of DCAHWP and DCHWT were compared for a 512 512 ‘Barbara’ image. The compression results for a CF of 1/32 clearly Indicate the superior performance of DCAHWP over DCHWT (Figure 12b, 12c). There is a significant blur- ring in the reconstructed image by DCHWT and hence the edges like eyes, nose and stripes ar e not distinct Fig- ure 12c. In contrast, the edge information is preserved to a large extent in reconstructed image by DCAHWP, which is manifested as the sharpness of the nose, eyes and stripes Figure 12c. The above results are supported by the percentage er- ror energy index as for DCAHWP, it is only about 2/3rd that of DCHWT Table 3. Example 4: To illustrate the performance superiority of DCAHWP due to its best basis selection over DCHWT,  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 73 Figure 9. Reconstruction of the signal in Figure 5 a. (a-d), Reconstructed signal for CF=1/8 by, (a) DBWT, (b) DBAWP, (c) DCHWT, (d) DCAHWP (e-h), error corresponding to (a-d). Figure 10. Speech signal. Figure 11. (a-d): Reconstructed speech for CF=1/8 by (a) DBWT (b) DBAWP, (c) DCHWT, (d) DCAHWP , (e-h): error corresponding to (a-d).  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 74 (a) (b) (c) Figure 12 Image reconstruction of the ‘Barbara’ image (512×512), (a) Original, (b) DCHWT (CF=1/32), (c) DCAHWP (CF=1/32). Figure 12. Image reconstruction of the ‘Barbara’ image (512×512), a) Original Barbara image, (b) Part of original w ith in the square(64×64), (c) DCHWT (CF=1/32), (d) DCAHWP (CF=1/32). (a) (b) (c) (d) (e) (f) Figure 14 Adaptive wavelet packet decomposition tree for the image in Figure 13a. (a-f): Decomposition levels 1-6 respec- tively. Shaded blocks indicate selected wavelet coefficients at each decomposition level.  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 75 Table 3. % error energy (% EE) for reconstruction of the image in Figure 12a with 1/32 coefficients (CF=1/32). Method % EE with CF = 1/32 DCHWT 1.1310 DCAHWP 0.7517 Table 4. % error energy (% EE) for reconstruction of the image in Figure 13(a) with 1/32 coefficients (CF= 1/32). Method % EE with CF= 1/32 DCHWT 4.3492 DCAHWP 0.9691 the two methods are applied to Barbara’ image Figure 13 aselecting a portion of it of size 64 64, which is marked by the square box in Figure 13 b. This small portion corresponds to an image with repetitive varia- tions in intensity (stripes). The best basis selection by the adaptive wavelet packet for this image is shown in the Figure 14. The subbands /scales in each wavelet packet decomposition level are depicted by square demarcations. The shaded squares are the selected subbands/scales for reconstruction. The percentage error energy by DCAHWP is about 1/5th of that by DCHWT in this case Table 4. The com- pressed image by DCHWT is a very crude representation of the image as the stripes are almost not visible (Figure 13c). But the stripes are clearly visible in the compressed image by DCAHWP Figure 13(d). 6. Conclusions An Adaptive Harmonic Wavelet Packet based on Dis- crete Cosine Transform (DCAHWP) was proposed. The implementation is simple as the DCT coefficients are real. The DCAHWP was achieved by using the entropy crite- rion realized by comparing the normalized energies of parents and children. The proposed DCAHWP performed better compared to Daubechies-2 based adaptive WP (DBAWP). For a compression factor (CF) of 1/8, for a 1-D signal and speech signal considered, the ratio of the percentage error energy (PEE) by DCAHWP to that by DBAWP was about 1/ 8 a n d 1/ 5, res pect ivel y . Compared to DCT based harmonic wavelet transform (DCHWT), as expected the proposed DCAHWP per- formed better as the ratio of the percentage error energies by DCAHWP to that by DCHWT better for 1D and speech, signals respectively were about 1/3 and 1/2, for a compression factor 1/8. The ratio of PEE for DCAHWP and that for DCHWT for an image ((512 512) Barbara) was 2/3 for a CF of 1/32. The compression by DCAHWP is superior in bringing out the edge information (high frequency con- tent) such as eyes, nose and stripes (texture), whereas that by DCHWT results in blurred images. Further for a textural image ((64 64) , a portion of the Barbara image) this normalized energy ratio between DCAHWP and that for DCHWT it was 1/5 for a CF of 1/32. But in all the cases, the reconstructed signals/images without compres- sion were almost identical to the original. The results clearly indicate that for signals character- ized by abrupt changes or images with rapid variations, the proposed DCAHWP provides significantly better compression performance compared to that of DCHWT. It has been found that the DCAHWP has a significantly better compression performance over the adaptive wave- let packet based on Daubechies-2, DBAWPT. REFERENCES [1] C. Sidney Burrus, R. A. Gopinath and H. T. Guo, “Intro- duction to Wavelets and Wavelet Transforms: A Primer,” Prentice-Hall, Inc., Upper Saddle River, 1998. [2] P. S. Addison, “The Illustrated Wavelet Transform Hand- Book,” Institute of Physics Publishing, London, 2002. [3] R. R. Coifman and M. V. Wickerhauser, “Entropy-Based Algorithms for Best Basis Selection,” IEEE Transactions on Information Theory, Vol. 38, No. 2, March 1992, pp. 713-718. [4] B. Liu, “Adaptive Harmonic Wavelet Transform with Applications in Vibration Analysis,” Journal of Sound and Vibration, Vol. 262, No. 1, 2003, pp. 45-64. [5] M. Kivanc Mihcak, K. Ramchandran and P. Moulin, “Adaptive Wavelet Packet Image Coding Using an Esti- mation-Quantization Framework,” Proceedings of Inter- national Conference on Image Processing, Chicago, USA, Vol. 1, 1998, pp. 92-96. [6] M. Musaruddin and A. Z. Kouzani, “Embedding Data in Images Using Wavelet Packets,” International Confer- ence IEEE TENCO, Vol. 2, 21-24 November 2004, pp. 120- 123. [7] D. E. Newland, “Harmonic Wavelet Analysis,” Proceed- ings: Mathematical and Physical Sciences, Vol. 444, No. 1917, 1993, pp. 203-225. [8] S. V. Narasimhan and M. Harish, “A New Spectral Esti- mator Based on Discrete Cosine Transform and Modified Group Delay,” Signal Processing, Vol. 86, No. 7, 2006, pp. 1586-1596. [9] S. V. Narasimhan, M. Harish, A. R. Haripriya and N. Basumallick, “Discrete Cosine Harmonic Wavelet Trans- form and Its Application to Signal Compression and Spectral Estimation Using Modified Group Delay,” Sig- nal, Image and Video Processing, Vol. 3, No. 1, February 2009, pp. 85-99. [10] S. V. Narasimhan, A. R. Haripriya and B. K. Shreyamsha Kumar, “Improved Wigner-Ville Distribution Perform- ance Based on Dct/Dft Harmonic Wavelet Transform and Modified Magnitude Group Delay,” Signal Processing,  A Discrete Cosine Adaptive Harmonic Wavelet Packet and Its Application to Signal Compression Copyright © 2010 SciRes. JSIP 76 Vol. 88, No. 1, 2008, pp. 1-18. [11] S. V. Narasimhan and A. Adiga, “Shift Invariant Discrete Cosine Harmonic Wavelet Transform and Its Application to Denoising,” Proceedings, IEEE International Confer- ence INDICON, Bangalore, 2007. [12] S. V. Narasimhan and S. Veena, “Signal Processing Prin- ciples and Implementation,” Alpha Science, Harrow, UK and Narosa publishers, New Delhi, India, 2008. [13] T. Gulzow, T. Ludwig and U. Heute “Spectral-Subtrac- tion Speech Enhancement in Multirate Systems with and without Non-Uniform and Adaptive Bandwidths,” Signal Processing, Vol. 83, No. 8, 2003, pp. 1613-1631. |

