Journal of Signal and Information Processing, 20 10 , 1, 44 -49
doi:10.4236/jsip.2010.11005 Published Online November 2010 (http://www.SciRP.org/journal/jsip)
Shifted Linear Interpolation Filter
H. Olkkonen1, J. T. Olkkonen2
1Department of Physics and Mathematics, University of Eastern Finland, Kuopio, Finland, 2VTT Technical Research Centre of
Finland, VTT, Finland
Received September 21st, 2010; revised November 8th, 2010; accepted November 15th, 2010.
ABSTRACT
Linear interpolation has been adapted in many signal and image processing applications due to its simple implementa-
tion and low computational cost. In standard linear interpolation the kernel is the second order B-spline


2
βt. In this
work we show that the interpolation error can be remarkably diminished by using the time-shifted B-spline


2
βt-
Δ
as
an interpolation kernel. We verify by experimental tests that the optimal shift is 0.25Δ=. In VLSI and microprocessor
circuits the shifted linear interpolation (SLI) algorithm can be effectively implemented by the z-transform filter. The
interpolation error of the SLI filter is comparable to the more elaborate higher order cubic convolution interpolation.
Keywords: Linear Interpolation, Cubic Convolution, B-splines, VLSI
1. Introduction
Linear interpolation plays an important role in modern
signal and image processing applications due to its sim-
ple implementation and low computational cost. Plonka
[1,2] has extensively studied the effect of the shifted in-
terpolation nodes on the approximation error in the B-
spline interpolation . According to the theoretical analysis
the shift 0

 yields the minimal error norm. Blu et al.
[3] applied the same idea to the piecewise-linear interpo-
lation. On the contrary, they observed that interpolation
error diminishes if the sampling knots are shifted by a
fixed amount. Through the theoretical considerations Blu
et al. [3] determined the optimal shift of the knots is
close to 1/5

 of the distance between the knots.
In this work we consider a modification of the linear
interpolation. In standard linear interpolation the kernel
is the second order B-spline 2()t

. Instead of shifting
the sampling knots we introduce the shifted linear inter-
polation (SLI), where the B-spline kernel has been
time-shifted by a fraction  of the sampling period. We
describe the z-transform SLI filter for efficient imple-
mentation of the shifted B-spline kernel 2()t


 es-
pecially for VLSI and microprocessor circuits.
2. Theoretical Considerations
2.1. B-Spline Signal Processing
B-spline approximation of the con tinu ous signal


x
t is
based on the summation [4]

 


p
k
x
tcktk




(1)
where


ck are the scale coefficients. The B-spline


pt

is constructed by convolving an indicator func-
tion


t

by itself



 
p times
pttt t
 



 (2)
where
10 1
() 0elsewhere
t
t 



 (3)
The linear interpolation is obtained in the case 2p


 


2
k
x
tcktk




(4)
where


2t
 is the triangle function Figure 1 defined as
2
for 0t<1
()2for1 t2
0elsewhere
tt
tt




 



(5)
2.2. Shifted Linear Interpolation
Let us consider th e approximation of the continuou s-time
signal


x
t by a summation of the shifted B-spline


2t








2
,
k
x
tcktk 



(6)
This work was supported by the National Technology Agency o
f
Finland (TEKES).

Shifted Linear Interpolation Filter
45
Figure 1. The shifted B-spline

2t
  .
where




,, 0,1ck is the scale sequence for the
time-shifted kernel. In the sequel we call (6) the shifted
linear interpolation (SLI). Usually the data points are
known in discrete time intervals

0, 1,2,tnTn.
In the z-transform domain we obtain



 

 
2
1
,
,1
ZxnXz CzZt
Cz z


 

 

(7)
The SLI filter is now obtained from (6) as




1
,1
Z
xndCzdd z


 

(8)
By inserting the scale sequence

,Cz from (7) we
finally have
 

 

1
1
1
1
,,
ddz
Z
xndX z
z
SLI dz Xz


 
 

(9)
where


,,SLI dz denotes the SLI filter.
2.3. Inverse SLI Filter
In some applications it is requ ired that the original signal
has to be reconstructed from the delayed one. In the gen-
eral case the SLI filter (9) has no stable inverse since the
roots of the nominator may lie outside the unit circle. For
0.25

 the roots are inside the unit circle in the range
00.25d

. The inverse SLI filter can be realized by
the inverse filtering procedure described in Appendix I.
3. Experimental
3.1. Experimental Verification of the SLI
Algorithm
We tested experimentally the quality of the SLI filter for
a variety of synthetic signals with varying frequency
components. The interpolation error was defined as the
absolute difference between the analytically calculated
and interpolated signal:

 
int
etxtxt . The time-
shift of the interpolation kernel was altered in the range
01

 . The interpolation error was strongly related
to the time-shift. Irrespective of the typ e of the signal the
minimum interpolation error was obtained in every case
at 0.25

. Figure 2 shows an example of the interpo-
lation error versus

for signal

sin 0.1t, when
0.5d

. The worst case is the linear interpolation
Figure 2. Interpolation error of function

0.1sinnin the case d=0.5 for piecewise-linear interpolation


0Δ= and for
SLI filter from=0.21Δto =0.25Δ.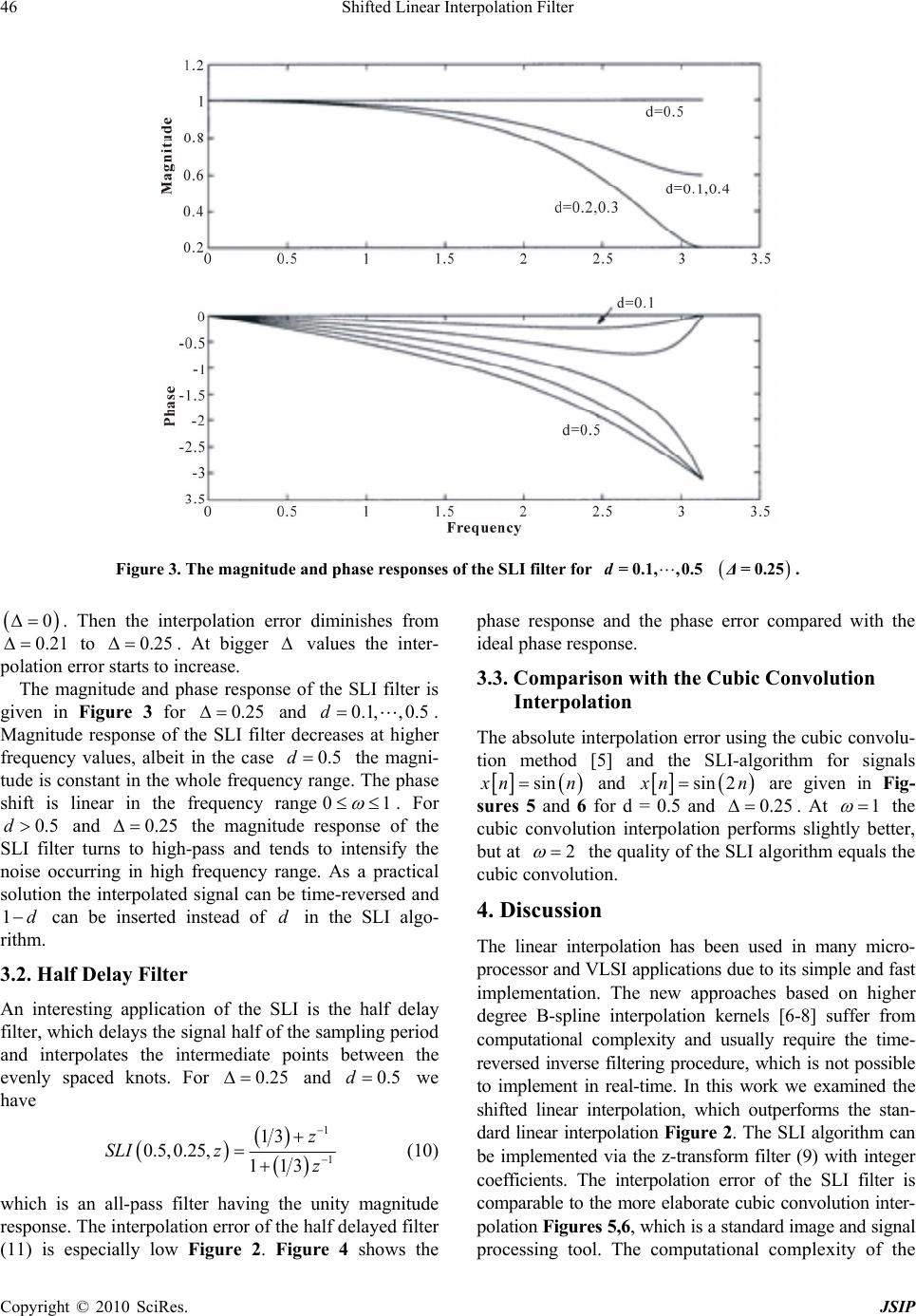

Shifted Linear Interpolation Filter
46
Figure 3. The magnitude and phase r esponses of the SLI filter for 0.1, ,0.5d=


=0.25Δ.

0. Then the interpolation error diminishes from
0.21 to 0.25 . At bigger  values the inter-
polation error starts to increase.
The magnitude and phase response of the SLI filter is
given in Figure 3 for 0.25 and 0.1, ,0.5d.
Magnitude response of the SLI filter decreases at higher
frequency values, albeit in the case 0.5d the magni-
tude is constant in the whole frequency range. The phase
shift is linear in the frequency range01

. For
0.5d and 0.25 the magnitude response of the
SLI filter turns to high-pass and tends to intensify the
noise occurring in high frequency range. As a practical
solution the interpolated signal can be time-reversed and
1d can be inserted instead of d in the SLI algo-
rithm.
3.2. Half Delay Filter
An interesting application of the SLI is the half delay
filter, which delays the signal half of the sampling period
and interpolates the intermediate points between the
evenly spaced knots. For 0.25 and 0.5d

we
have



1
1
13
0.5,0.25, 113
z
SLI zz



 (10)
which is an all-pass filter having the unity magnitude
response. The interpolation error of the half delayed filter
(11) is especially low Figure 2. Figure 4 shows the
phase response and the phase error compared with the
ideal phase response.
3.3. Comparison with the Cubic Convolution
Interpolation
The absolute interpolation error using the cubic convolu-
tion method [5] and the SLI-algorithm for signals




sin
x
nn and



sin 2
x
nn are given in Fig-
sures 5 and 6 for d = 0.5 and 0.25 . At 1


the
cubic convolution interpolation performs slightly better,
but at 2


the quality of the SLI algorithm equals the
cubic convolution.
4. Discussion
The linear interpolation has been used in many micro-
processor and VLSI applications due to its simple and fast
implementation. The new approaches based on higher
degree B-spline interpolation kernels [6-8] suffer from
computational complexity and usually require the time-
reversed inverse filtering procedure, which is not possible
to implement in real-time. In this work we examined the
shifted linear interpolation, which outperforms the stan-
dard linear interpolation Figure 2. The SLI algorithm can
be implemented via the z-transform filter (9) with integer
coefficients. The interpolation error of the SLI filter is
comparable to the more elaborate cubic convolution inter-
polation Figures 5,6, which is a standard image and signal
processing tool. The computational complexity of the

Shifted Linear Interpolation Filter
47
Figure 4. Comparison of the phase responses of the piecewi se -line ar interpolation and the SLI fil t er(d = 0.5, 0.25Δ=).
Figure 5. The absolute interpolation error yielded by the
SLI algorithm (d = 0.5, 0.25Δ=) and the cubic convolu-
tion interpolation for the sinusoidal signal




xn=sinn.
cubic convolution method is significantly higher com-
pared with the SLI algorithm .
The interpolation function used as a kernel in the SLI
algorithm correspond the B-spline order p = 2 Figure 1.
The B-spline

2t

h as the z- tra nsf orm

1
1z

 .
Figure 6. The absolute interpolation error yielded by the
SLI algorithm (d = 0.5, 0.25Δ=) and the cubic convolu-
tion interpolation for the sinusoidal signal




2xn=sin n.
Probably the main reason for the effectiveness of the SLI
comes from the two term z-transform, which allows the
solution of the scale coefficient sequence

,Czin (7).
This leads to the definition of the SLI filter (9). As a sur-

Shifted Linear Interpolation Filter
48
prising experimental observation of the SLI algorithm is
the strong dependence of the interpolation error on the
time shift . Our comparisons using a variety of func-
tions with different waveforms and frequency content
showed that every time the interpolation error attains its
minimum at 0.25 . Previously Plonka [1,2] has
studied the B-spline interpolation with shifted nodes. In
the theoretical analysis the shift parameter 0


yielded the minimal error norm. Blu et al. [3] conducted
theoretically the piecewise-linear interpolation error ver-
sus the shift

in the measurement knots. Their analysis
predicted the optimal choice 0.21

. Blu et al. [3]
used a pre-filter to shift the measurement knots and then
the standard piecewise linear interpolation for computa-
tion of the interpolated signal. An advantage in this pro-
cedure is that the prefiltered signal can be directly im-
plemented by any existing linear interpolation hardware,
while the implementation of the SLI filter needs a new
hardware design.
An essential observation in this work is that the SLI
filter has low-pass frequency response characteristics
only in the range 00.5d . For 0.5d the fre-
quency response of the SLI filter turns to high-pass and
intensifies the noise occurring in high frequency range.
The noise interference for 0.5d can be avoided by
time reversing the interpolated signal. Then 1d

can
be inserted instead of d in the SLI algorithm.
A shortcoming in the SLI algorithm is the phase error
occurring in the high frequency range compared with the
linear interpolation. Fortunately, in most of the signal
processing applications the signal is band limited and the
high frequency band 2

 contains only some noise
components.
An interesting observation is that for 0.5d and
0.25 the half delay SLI algorithm reduces to the
simple all-pass filter (10), which has the unity magnitude
response and the phase response is close to the ideal
phase response in the range 01

. If the signal
bandwidth is limited to this range the SLI algorithm
yields interpolation precision and accuracy, which is
comparable to the more elaborate interpolation methods.
The interpolation of intermediate points between the
uniformly distributed knots is probably the most fre-
quently used operation is image and signal processing.
The half delay filters are also important tools in con-
struction of shift invariant wavelet transform [9]. The
half delay SLI filter (10) can be readily applied to replace
the more elaborate half delay filters based on the Thiran
filters [10]. For 00.25d and 0.25 the SLI filter
has a stable inverse. If the original data points have to be
reconstructed from the interpolated ones, the inverse SLI
filter for higher values of d can be realized by using the
inverse filtering procedure (Appendix I).
5. Conclusions
In signal and image processing applications linear inter-
polation has been frequently used due to its simple im-
plementation and low computational cost. In standard
linear interpolation the kernel is the second order
B-spline


2t
 . We show in this work that the interpo-
lation error can be remarkably reduced by adapting the
time-shifted B-spline


2t
  as an interpolation ker-
nel. By experimental tests we verify that the optimal shift
is 0.25

. The shifted linear interpolation (SLI) algo-
rithm can be effectively implemented by the z-transform
filter in VLSI and microprocessor applications. The in-
terpolation error of the SLI filter is comparable to the
more elaborate cubic convolution interpolation. The fu-
ture research goal is to extend the time-shifted interpola-
tion kernel to higher order B-splines.
Appendix I. Implementation of the inverse fil-
ter


1,,SLI dz  for 0.25

 and 0.25d.
By denoting the interpolated signal by






YzZxn d the inverse filter


1,,SLI dz  is





1
1
1
1
,, 1
X
z
z
SLI dzYz
ddz



 
 
 
(11)
The inverse filter


1,,SLI dz

 is not stable which is
not stable for 0.25

 and 0.25d , since the root
in the denominator is outside the unit circle. However,
the inverse filter can be implemented by the following
inverse filtering procedure. First we replace z by z-1





 
11
11
1
1
1
,, 1
Xz z
SLI dzddz
Yz




 
 
 
(12)
The inverse filter

11
,,SLIdz

 is stable for
0.25

 and 0.25d. The

1
X
z and


1
Yz

are the z-transforms of the time reversed signal


x
Nn

and the interpolated signal


y
Nn

. The
following Matlab program ISLI.m demonstrates the
computation proced ure.
function x = ISLI(y,d,delta)
y = y(end:-1:1);
x = filter([delta 1-delta],[delta+d 1-delta-d],y);
x = x(end:-1:1);
REFERENCES
[1] G. Plonka, “Periodic Spline Interpolation with Shifted
Nodes,” Journal of Approximation Theory, Vol. 76, No. 1,
1994, pp. 1-20.
[2] G. Plonka, “Optimal Shift Parameters for Periodic Spline
Interpolation,” Numerical Algorithms, Vol. 6, No. 2, 1994,

Shifted Linear Interpolation Filter
49
pp. 297-316.
[3] I. J. Schoenberg, “Contribution to the Problem of Ap-
proximation of Equidistant Data by Analytic Functions,”
Quarterly of Applied Mathematics, Vol. 4, No. 1, 1946,
pp. 45-99, 112-141.
[4] T. Blu, P. Thevenaz and M. Unser, “Linear interpolation
revitalized”, IEEE Trans. Image Process. Vol. 13, No. 5,
pp. 710-719, May 2004.
[5] R. G. Kay, “Cubic Convolution Interpolation for Digital
Image Processing,” IEEE Transactions on Acoustics,
Speech, Signal Processing, Vol. 29, No. 6, December
1981, pp. 1153-1160.
[6] P. Thevenaz, T. Blu and M. Unser, “Interpolation Revis-
ited,” IEEE Transactions on Medical Imaging, Vol. 19,
No. 7, July 2000, pp. 739-758.
[7] J. T. Olkkonen and H. Olkkonen, “Fractional Delay Filter
Based on B-Spline Transform,” IEEE Signal Processing
Letters, Vol. 14, No. 2, February 2007, pp. 97-100.
[8] J. T. Olkkonen and H. Olkkonen, “Fractional Time-Shift
B-Spline Filter,” IEEE Signal Processing Letters, Vol. 14,
No. 10, October 2007, pp. 688-691.
[9] H. Olkkonen and J. T. Olkkonen, “Half Delay B-Spline
Filter for Construction of Shift Invariant Wavelet Trans-
form,” IEEE Transactions on Circuits and Systems II,
Vol. 54, No. 7, July 2007, pp. 611-615.
[10] I. W. Selesnick, “The Design of Approximate Hilbert
Transform Pairs of Wavelet Bases,” IEEE Transactions
on Signal Processing, Vol. 50, No. 5, May 2002, pp.
1144-1152.