Circuits and Systems
Vol.07 No.08(2016), Article ID:67366,8 pages
10.4236/cs.2016.78133
Design of Compact Baugh-Wooley Multiplier Using Reversible Logic
V. Rajmohan, O. Uma Maheswari
Department of Electronics and Communication Engineering, College of Engineering, Chennai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 April 2016; accepted 15 May 2016; published 15 June 2016
ABSTRACT
In today’s digital era, developing digital circuits is bounded by the research towards investigating various nano devices. This paper provides the design of compact Baugh-Wooley multiplier using reversible logic. Even though various researches have been done for designing reversible multiplier, this work is the first in the literature to use Baugh-Wooley algorithm using reversible logic. In this work, a new 5 × 5 reversible multiplier cell is proposed which will be useful in designing Baugh-Wooley multiplier. The proposed single multiplier cell is able to perform addition of a 1 × 1 product with the sum and carry from the previous cell. This reversible multiplier cell is useful in building up regularity in the array multipliers. The Toffoli gate synthesis of the proposed reversible multiplier cell is also given.
Keywords:
Multiplier, Baugh-Wooley, Low-Power, Reversible Logic, Quantum Computer

1. Introduction
In today’s digital era, developing digital circuits is bounded by the research towards investigating various nano devices to provide substitution for CMOS technology. As the nano devices are developed, the density of digital chips is being increased naturally seeking the solution for the power consumption and the heat dissipation developed by this power consumption. This scenario motivates the study of reversible computing field. The origin of the reversible computing is the research work done by R. Landauer in early 1960’s stating that irrespective of the realization technique, the irreversible hardware computation results energy dissipation due to information loss [1] . According to R. Landauer, loss of one bit information dissipates at least KTln2 joules of energy in the form of heat, where the Boltzmann’s constant is represented by K and the absolute temperature is represented by T. As per C. H. Bennett’s research, the circuits built using reversible logic gates will prevent KTln2 joules of energy dissipation in a circuit [2] . A circuit will be known as reversible if it can bring back the inputs from the outputs. Also the relationship between the inputs and outputs should be maintained as one-to-one and unique. This constraint forces the number of inputs to be equal to the number of outputs [3] [4] .
Hence reversible logic is being applied in various research domains like DNA computing, nanotechnology, Low Power CMOS design and quantum computing. The quantum circuits can be constructed only with reversible logic gates. Besides, synthesizing reversible logic circuits is much difficult than conventional irreversible logic circuits due to the constraints. In the reversible logic circuit design, fan-out and feedback are not permitted [4] . Apart from that the reversible logic circuit should use 1) lowest number of reversible gates, 2) lowest number of garbage outputs, 3) lowest number of constant inputs. The garbage output is the one which is not used for further computations. The additional input that is included to the irreversible function to convert it reversible is called constant input [4] .
In the recent years various reversible multiplier designs have been proposed [5] - [9] . In [5] , the design deals with 4 × 4 parallel multiplier. It has been done in two steps as follows: 1) Partial Product Generation, 2) Multi Operand Addition. To generate the partial products, 16 Peres gates have been used, for 16 one-bit multiplication arrays. Then the four operand addition has been performed using Peres gates and Double Peres gates. In [6] , the authors have proposed a new reversible gate called as HNG gate. This work also involves two steps as in [5] . The partial products have been generated using Peres gates. HNG gates are used in the second step, Multi operand addition. The work [7] also follows the same strategy as the previous two works, multiplication in two steps. In this work, the authors have proposed Peres Full Adder Gate (PFAG). In this work also, like the previous works, the partial products have been generated using Peres gate. The PFAG gate is used in the multi operand addition. In [8] , the authors have proposed a new reversible gate called as RAM gate. This gate is mainly used as a copying gate as fan-out is not allowed in reversible logic design. This gate has been used in the partial product generation. In the second step, the multi operand addition, Peres gates and Double Peres gates have been used. In our work, we have proposed a reversible multiplier cell which can be efficiently used in the Baugh Wooley multiplier.
The organization of the paper is as follows. Section 2 is an overview of basic reversible gates. Section 3 is an overview of Baugh-Wooley multiplier. A detailed representation and explanation is done in this section. The proposed reversible multiplier design and its functions are discussed in section 4. The results and discussions of the proposed reversible Baugh-Wooley multiplier are presented in section 5. Conclusion is in section 6.
2. Reversible Logic Gates
A circuit will be known as reversible if it can bring back the inputs from the outputs. Also the relationship between the inputs and outputs should be maintained as one-to-one and unique. This constraint forces the number of inputs to be equal to the number of outputs. This section deals with the preliminary reversible gates available in the literature.
Figure 1 shows a basic 2 × 2 reversible gate known as Feynman Gate [10] and its quantum representation. Feynman Gate (FG) can be used as a copying gate. Since in reversible circuits the fan-out greater that one is not permitted, this gate is useful for duplicating the inputs. When the input B = “0”, the outputs P = “A” and Q = “A”. This gate is also known as Controlled-Not gate. When the input A = “1”, the output Q produces the complement of A.
Figure 2 is called as 3 × 3 Toffoli gate [11] and also code-named as the “controlled-controlled-not” gate, which depicts its action. The number of inputs and outputs are three in count; if the first two bits A and B are set, the third bit will be inverted, otherwise all bits will keep on the same value. When the input C = “1”, the output R produces the AND function between the inputs A and B.
Figure 1. 2 × 2 Feynman Gate (FG).
Figure 3 is a 3 × 3 Fredkin gate [11] . If the input A = “0”, then Q = “B” and R = “C”. Whereas if the input A = “1”, then Q = “C” and R = “B”. Hence this is also called as Swap gate. The functionality shows that this gate will be useful in designing a n-bit MUX with (n + 1) garbage output.
Figure 4 is a 3 × 3 Peres Gate (PG) [12] . It is also known as New Toffoli Gate (NTG). Function wise Peres Gate will be equal with the bit conversion generated by a Toffoli Gate succeeded by a Feynman Gate.
Figure 2. Toffoli Gate (TG).
Figure 3. Fredkin Gate (FRG).
Figure 4. Peres Gate (PG).
3. Baugh-Wooley Multiplier
When we are performing the signed n × n multiplication there will be no difference if the result has the same bit-width as the inputs. For Eg: the multiplication of two numbers “−2” and “3” results in “−6”. Its binary representation is (1110)2 × (0011)2 = (1010)2. But what happens if we want the result to be in “2n” bits. Either we need to use sign extension or “2n × 2n” array multiplier. One of the efficient algorithms to handle such situation is the Baugh-Wooley multiplication. This design method has been established in order to design structured multipliers, appropriate for 2’s complement numbers [13] . Let the numbers to be multiplied be A and B. Here “A” denotes the n-bit multiplier and “B” denotes the n-bit multiplicand. The multiplier A and the multiplicand B can be represented as
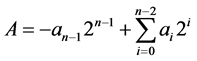 (1)
(1)
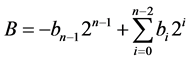 (2)
(2)
where the bits in A and B are denoted as ai’s and bi’s, respectively, and an−1 and bn−1 are the sign bits. The below equation gives the n * n product, P = A × B:
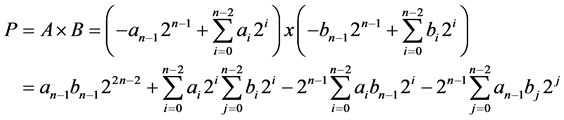 . (3)
. (3)
The final product could be generated by subtracting the last two positive terms from the first two terms. Instead of doing subtraction operation as in the normal multipliers, it is possible to obtain the two’s complement of the last two terms and add all the terms to deliver the final product. The last two terms will be of n − 1 bits length where each term has the binary extension from position 2n−1 up to 22n−3. In contrast the final product is 2n bits which extend the binary weight from 20 up to 22n−1. As a first step pad each of the last two terms in the product P with zeros to obtain a 2n-bit number to aid adding it with the other terms. Later the padded terms extend in binary weight from 20 up to 22n−1. Let X be one of the last two terms that can represent it with zero padding as
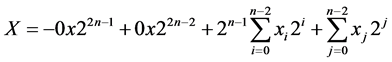 . (4)
. (4)
The final n * n product, P = A × B is given by:
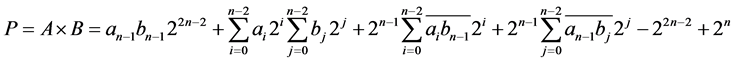 . (5)
. (5)
Let two 4-bit binary numbers be A and B, then the product, P = A × B will be 8 bit long and is
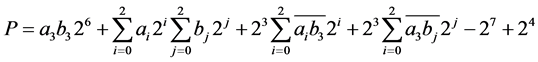 . (6)
. (6)
The block diagram representation of 4 bit Baugh-Wooley multiplier is shown in Figure 5.
4. Proposed Reversible Logic Gates
In the block diagram shown in Figure 5, three types of cells are used. The yellow cells represent the full adder.
Figure 5. Block diagram of 4-bit Baugh-Wooly multiplier.
The black cells are representing the multiplier cell used for 2’s complement numbers. The grey cells represent the multiplier cell. Each of the multiplier cell receives four inputs namely, the multiplier input (horizontal-green line), multiplicand input (vertical-red line), carry from previous cells (vertical-black line) and sum from previous cells (diagonal-black line). They produce two outputs namely sum output (diagonal-black line) and carry output (vertical black line).
In this work we are proposing two reversible multiplier cells representing black and grey cells. Since each cell is having four inputs and two outputs, the reversible multiplier cell, in order to maintain the reversible constraints it is developed as a cell having five inputs and five outputs. Out of this, three outputs are maintained as garbage outputs. Garbage outputs are by definition don’t care outputs and thus can be left unspecified leading to an incompletely specified function [14] . The Reversible Multiplier cell (MC) is shown in Figure 6. It is a 5 × 5 reversible logic. This is the first 5 × 5 reversible multiplier cells proposed in the literature. Out of the five outputs, two outputs (Q and R) are left unspecified, since these are the garbage outputs. The functions S and T will produce sum and carry outputs respectively.
The Toffoli gate representation of the proposed Reversible Multiplier Cell is given in Figure 7. The representation has the Gate Count of 15. The Quantum cost is 69. The number of two-Qubit gates is 55.
The Reversible Complement Multiplier Cell (CMC) is shown in Figure 8. It is also a 5 × 5 reversible logic gate. Out of the five outputs, two outputs (Q and R) are left unspecified, since these are the garbage outputs. The functions S and T will produce sum and carry outputs respectively of the complement function of the Baugh- Wooley structure.
Figure 6. Reversible multiplier cell (MC).
Figure 7. Synthesis of reversible multiplier cell.
These proposed multiplier cells are having one constant input. These cells will function as a multiplier circuit when the input “E = 0”. The input A is the multiplier bit. The input B is the multiplicand bit. The input C is the carry input from the previous cells. The input D is the sum input from the previous cells. For the first level the inputs C and S will be “0”. The outputs P, Q and R are considered as garbage outputs. Since this is an incompletely specified reversible logic gates the functions Q and R are not specified.
5. Results and Discussions
The reversible multiplier designs available in the literature are for the array multipliers. There is no any specific application of any algorithm except [15] . Since this work may be the first in the literature we can’t compare and evaluate with other similar proposals. However this work is compared and evaluated with the other array multiplier designs available in the literature. Therefore the proposed multiplier cells are evaluated based on the Gate count, Garbage inputs and Garbage outputs. Since the proposed cells are incompletely specified cells we could not generate the Quantum cost and therefore we could not evaluate the proposed gates based on the Quantum cost.
5.1. Gate Count & Hardware Complexity
Measuring the reversible logic design in terms of number of gates is one of the major factors. In [5] , the design requires a total of 40 reversible gates, [9] requires 42, total number of gates required is 44 in [7] and in [8] the number of gates required is 32 gates. The proposed Baugh-Wooley multiplier design requires 20 gates. Therefore, the hardware intricacy of the proposed design is less compared to the existing approaches.
5.2. Constant Inputs
One of the major factors in the design of a reversible logic circuit is the number of constant inputs. The input used as a control input by connecting to either logical low or logical high to get the required function at the output is called garbage/constant input. The proposed reversible Baugh-Wooley multiplier design requires 16 constant inputs, but the design in [5] [7] - [9] requires 52, 40, 44 and 42 respectively. Hence the proposed Baugh- Wooley Multiplier design is better than existing designs.
5.3. Garbage Outputs
The number of output of the reversible gate that is not making useful functions is referred as garbage output. Other constraint in designing reversible logic circuit is optimizing garbage outputs. The proposed reversible Baugh- Wooley multiplier design produces 48 garbage outputs, but the design in [5] [7] - [9] produces 52, 52, 40 and 49 garbage outputs respectively. Therefore, it is clear that this is the better design than the existing counterparts.
The conclusion of the above discussion is that, it is evident that the proposed reversible Baugh-Wooley multiplier circuit design is better than the existing designs with respect to gate counts, garbage inputs and garbage outputs.
5.4. Evaluation of the Proposed Reversible Baugh-Wooley Multiplier Circuit
The proposed reversible Baugh-Wooley multiplier circuit is more efficient compared to the existing circuits presented by [5] [7] - [9] . This can be understood easily with the help of the comparison results shown in Table 1.
6. Conclusion
In this work, the design of 5 × 5 reversible Multiplier Cell (MC) and reversible Complement Multiplier Cell is proposed. These are the first 5 × 5 reversible multiplier cells proposed in the literature. These reversible multiplier cells are targeted for reversible Baugh-Wooley multiplier design. The proposed reversible multiplier cells are capable of multiplying 2 bits in the current array and add the result with the sum and carry outputs of previous array. The Toffoli gate synthesis of the proposed reversible multiplier cell is also given. The functionality of the multiplier cell was verified with RC viewer. This design is useful in the multiplier design with reduced number of gates and constant inputs. Even the proposed design is having moderate garbage outputs; we can conclude that this design is better in terms of number of gates and constant inputs. The number of gates, constant inputs and garbage outputs
Figure 8. Complement reversible multiplier cell (CMC).
Table 1. Comparison of proposed and existing design.
are analyzed. It is comprehended that the number of gates, the constant inputs and garbage outputs values are fewer in number in the proposed design compared to the existing approaches. The design can be enhanced to construct n × n reversible Baugh-Wooley multiplier circuit.
Cite this paper
V. Rajmohan,O. Uma Maheswari, (2016) Design of Compact Baugh-Wooley Multiplier Using Reversible Logic. Circuits and Systems,07,1522-1529. doi: 10.4236/cs.2016.78133
References
- 1. Landauer, R. (1961) Irreversibility and Heat Generation in the Computing Process. IBM Journal of Research and Development, 5, 183-191.
http://dx.doi.org/10.1147/rd.53.0183 - 2. Bennett, C.H. (1973) Logical Reversibility of Computation. IBM Journal of Research and Development, 17, 525-532.
http://dx.doi.org/10.1147/rd.176.0525 - 3. Perkowski, M., Al-Rabadi, A., Kerntopf, P., Buller, A., Chrzanowska-Jeske, M., Mishchenko, A., Azad Khan, M., Coppola, A., Yanushkevich, S., Shmerko, V. and Jozwiak, L. (2001) A General Decomposition for Reversible Logic. Fifth Reed-Muller Workshop 2001, Starkville, August 2001, 119-138.
- 4. Perkowski, M. and Kerntopf, P. (2001) Reversible Logic. 27th EUROMICRO Conference, Warsaw, Poland, September 2001.
- 5. Bhagyalakshmi, H.R. and Venkatesha, M.K. (2010) An Improved Design of a Multiplier Using Reversible Logic Gates. International Journal on Engineering Science and Technology, 2, 3838-3845.
- 6. Haghparast, M., Jassbi, S.J., Navi, K. and Hashemipour, O. (2008) Design of a Novel Reversible Multiplier Circuit Using HNG Gate in Nanotechnology. World Applied Sciences Journal, 3, 974-978.
- 7. Islam, M.S., et al. (2009) Low Cost Quantum Realization of Reversible Multiplier Circuit. Information Technology Journal, 8, 208-213.
http://dx.doi.org/10.3923/itj.2009.208.213 - 8. Rangaraju, H.G., Babu Suresh, A. and Muralidhara, K.N. (2013) Design of Efficient Reversible Multiplier. In: Meghanathan, N., Nagamalai, D. and Chaki, N., Eds., Advances in Computing and Information Technology, Springer, Berlin Heidelberg, 571-579.
http://dx.doi.org/10.1007/978-3-642-31600-5_56 - 9. Zhou, R., et al. (2010) Comment on Design of a Novel Reversible Multiplier Circuit using HNG Gate in Nanotechnology. World Applied Sciences Journal, 10, 161-165.
- 10. Feynman, R. (1985) Quantum Mechanical Computers. Optical News, 11, 11-20.
http://dx.doi.org/10.1364/ON.11.2.000011 - 11. Fredkin, E. and Toffoli, T. (1982) Conservative Logic. International Journal of Theoretical Physics, 21, 219-253.
http://dx.doi.org/10.1007/BF01857727 - 12. Peres, A. (1985) Reversible Logic and Quantum Computers. Physical Review A, 32, 3266-3276.
http://dx.doi.org/10.1103/PhysRevA.32.3266 - 13. Mohanty, P. (2012) An Efficient Baugh-Wooley Architecture for Both Signed & Unsigned Multiplication. International Journal of Computer Science & Engineering Technology (IJCSET), 3, No. 4.
- 14. Wille, R. and Drechsler, R. (2010) Towards a Design Flow for Reversible Logic. Springer, Netherlands, 29.
http://dx.doi.org/10.1007/978-90-481-9579-4 - 15. Thapliyal, H. and Srinivas, M.B. (2006) Design of Wallace Tree Multiplier and Other Components of a Quantum ALU Using Reversible TSG Gate. SPIE Proceedings, 6264, 62640H.










