Applied Mathematics, 2010, 1, 431-438
doi:10.4236/am.2010.15057 Published Online November 2010 (http://www.SciRP.org/journal/am)
Analytical and Numerical Solutions for a Rotating Annular
Disk of Variable Thickness
Ashraf M. Zenkour1,2, Daoud S. Mashat1
1Department of Mathematics, Faculty of Science, King AbdulAziz University,
Jeddah, Saudi Arabia
2Department of Mathematics, Faculty of Science, Kafrelsheikh University, Kafr El-Sheikh, Egypt
Received July 19, 2010; revised October 9, 2010; accepted October 12, 2010
Abstract
In this paper, the analytical and numerical solutions for rotating variable-thickness solid disk and numerical
solution for rotating variable-thickness annular disk are presented. The outer edge of the solid disk and the
inner and outer edges of the annular disk are considered to have clamped boundary conditions. Two different
cases for the radially varying thickness of the solid and annular disks are given. The numerical solution as
well as the analytical solution is available for the first case of the solid disk while the analytical solution is
not available for the second case of the annular disk. Both analytical and numerical results for displacement
and stresses will be investigated for the first case of radially varying thickness. The accuracy of the present
numerical solution is discussed and its ability of use for the second case of radially varying thickness is in-
vestigated. Finally, the distributions of displacement and stresses will be presented and the appropriate com-
parisons and discussions are made at the same angular velocity.
Keywords: Rotating, Annular Disk, Solid Disk, Finite Difference Method
1. Introduction
The problems of rotating solid and annular disks have
been performed under various interesting assumptions
and the topic can be easily found in most of the standard
elasticity books [1-5]. Most of the research works are
concentrated on the analytical solutions of rotating disks
with simple cross-section geometries of uniform thick-
ness and especially variable thickness [6-14]. The ana-
lytical elasticity solutions of such rotating disks are avai-
lable in many books of elasticity.
As many rotating components in use have complex
cross-sectional geometries, they cannot be dealt with
using the existing analytical methods. Numerical me-
thods, such as the finite element method [15], the
boundary element method [16] and Runge-Kutta’s algo-
rithm [17], can be applied to cope with these rotating
components.
In this paper, we will present the analytical solution
for the rotating solid disk with arbitrary cross-section of
continuously variable thickness. In the following, a
unified governing equation will be first derived from the
basic equations of the rotating disks and the proposed
stress-strain relationship. Next, finite difference method
(FDM) is introduced to solve the governing equation. A
comparison between both analytical and numerical
solutions is made. The accuracy of the numerical solu-
tion is used to find the displacement and stresses of
rotating variable-thickness annular disk whose analytical
solution is not available. Finally, a number of numerical
examples are given to demonstrate the validity of the
proposed method.
2. Basic Equations
As the effect of thickness variation of rotating disks can
be taken into account in their equation of motion, the
theory of the variable-thickness disks can give good
results as that of the uniform-thickness disks as long as
they meet the assumption of plane stress. After consi-
dering this effect, the equation of motion of rotating
disks with variable thickness can be written as

22
d0,
dr
hrhh r
r

  (1)
where r

and


are the radial and circumferential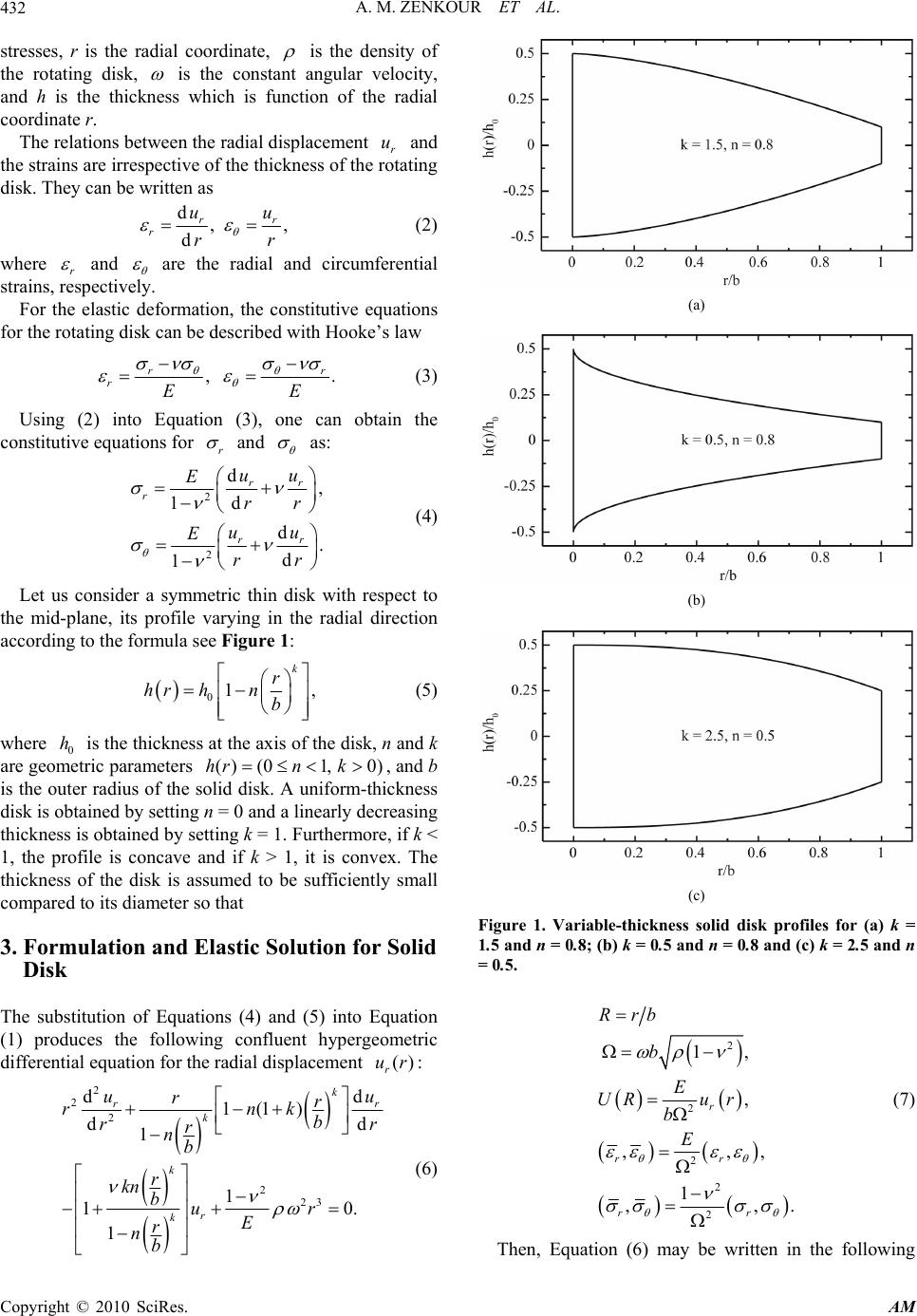

A. M. ZENKOUR ET AL. 432
stresses, r is the radial coordinate,

is the density of
the rotating disk,

is the constant angular velocity,
and h is the thickness which is function of the radial
coordinate r.
The relations between the radial displacement r u and
the strains are irrespective of the thickness of the rotating
disk. They can be written as
d,,
d
rr
r
uu
rr

  (2)
where r

and


are the radial and circumferential
strains, respectively.
For the elastic deformation, the constitutive equations
for the rotating disk can be described with Hooke’s law
,.
rr
rEE



 



(3)
Using (2) into Equation (3), one can obtain the
constitutive equations for r

and


as:
2
2
d,
d 1
d.
d 1
rr
r
rr
uu E
rr
uu E
rr













(4)
Let us consider a symmetric thin disk with respect to
the mid-plane, its profile varying in the radial direction
according to the formula see Figure 1:

01,
k
r
hrhn b








(5)
where 0 h is the thickness at the axis of the disk, n and k
are geometric parameters () (01,0)hrn k

 , and b
is the outer radius of the solid disk. A uniform-thickness
disk is obtained by setting n = 0 and a linearly decreasing
thickness is obtained by setting k = 1. Furthermore, if k <
1, the profile is concave and if k > 1, it is convex. The
thickness of the disk is assumed to be sufficiently small
compared to its diameter so that
3. Formulation and Elastic Solution for Solid
Disk
The substitution of Equations (4) and (5) into Equation
(1) produces the following confluent hypergeometric
differential equation for the radial displacement ():
r
ur




2
2
2
2
23
dd
1(1) d
d1
1
10.
1
k
rr
k
k
r
k
uu rr
rnk
br
rr
nb
r
kn bur
E
r
nb









 




(6)
(a)
(b)
(c)
Figure 1. Variable-thickness solid disk profiles for (a) k =
1.5 and n = 0.8; (b) k = 0.5 and n = 0.8 and (c) k = 2.5 and n
= 0.5.

 
 
 
2
2
2
2
2
1,
,
,,,
1
,,.
r
rr
rr
Rrb
b
E
URu r
b
E


 
 

 

 





(7)
Then, Equation (6) may be written in the following

A. M. ZENKOUR ET AL. 433
simple form


2
2
2
3
11
dd
d d1
11 0.
1
k
k
k
k
nkRR
UU
RR
RnR
nkR
UR
nR








(8)
The general solution of the above equation can be
written as

112 2,URCFRCF RPR  (9)
where 1
C and 2 C are arbitrary constants and 1
F
and
2
F
are given by:
 




1,, ,,
k
FR RHnR    (10)
 

2
11,1,2 ,,
k
FR HnR
R
   (11)
in which


2
2
41
11 ,
22
41
11 2
,1.
22
kk
kk
kk
kk k








 
(12)
The functions ([,], [],)
H
z



are the generalized
hyper-geometric functions,
 


0
,, ,,
!
0, 1,
qq
q
qq
H
zz
q
z

 





 (13)
where ()
q

is the Pochhammer symbol given by
 

12... 1,
q
q
q



 
 (14)
in which

represents Gamma function.
The term()PR in Equation (9) is the particular
solution of Equation (8) which can be written as


   
22
21
2
12
4dd,
RFRRF R
PRkF RRFRR

 





(15)
where

 






14 213
122 221,
kk
nkkRFFkFkF nkRF 


 

 (16)
in which
 




31,1,1 ,,
k
FR RHnR    (17)
 

4
12,2,3,,
k
FR HnR
R
   (18)
The substitution of Equation (9) into Equation (4) with
the aid of the dimensionless forms given in Equation (7)
gives the radial and circumferential stresses in the forms
of (19) and (20):
 
21
21
1132 24
11
11 d
,
22d
k
k
r
knR
knRP P
RCFF CFF
Rk RkRR


 






 






(19)
 
21
21
1132 24
11
11 d
.
22d
k
kknR
knRP P
RCFF CFF
Rk RkRR


 
 





 






(20)
4. Analytical Solution for the Rotating Solid
Disk
The analytical elastic solution for the solid disk with
variable-thickness is completed by the application of the
boundary conditions. Since the radial displacement
should be vanished and the stresses should be finite at
the center of the disk, then the constant 2
C vanishes.
The radial displacement is vanished at the outer edge of
the disk, r = b or (R = 1), hence



1
1
1.
1
P
CF  (21)
So, one can easily obtain the solution for the present
rotating variable-thickness solid disk by the substitution
of Equation (21) into Equations (9), (19) and (20).
5. Finite Difference Algorithm for Solid Disk
The resolution of the elastic problem of rotating disk
with variable thickness is to solve a second-order
differential equation, Equation (8), under the given
boundary conditions. This equation can be written in the
following general form:


 
,
01,010,
UpRUqRUsR
RU U

 
 (22)
where the prime (') denotes differentiation with respect
to R and

A. M. ZENKOUR ET AL. 434




 


2
11 ,
1
11 ,
1
.
k
k
k
k
nkR
pR nR R
nkR
qR nR R
sR R


 



(23)
It is clear that the above problem has a unique solution
because (), (),pRqR and ()
s
R are continuous on the
given interval ]0,1] and () 0qR  on ]0,1]. The linear
second-order boundary value problem given in Equation
(22) requires that difference-quotient approximations be
used for approximating U and U . First we select an
integer 0N and divided the interval ]0,1] into
(1)N equal subintervals, whose end points are the
mesh points ,
i
RiR for 0,1,..., 1,iN where
1/(1)RN . At the interior mesh points, ,
i
R
1, 2,...,,iN the differential equation to the
approximated is
 


.
iiiiii
URpRURqR URsR
 
 (24)
If we apply the centered difference approximations of
()
i
UR
 and ()
i
UR
 to Equation (24), we arrive at the
system:
 
  
2
1
2
1
12()
2
1,
2
ii ii
ii i
RpRUR qRU
RpRUR sR





 
 



 


(25)
for each 1, 2,...,.iN The N equations, together with
the boundary conditions
0
1
0,
0,
N
U
U

 (26)
Are sufficient to determine the unknowns ,
i
U
0,1, 2,...,1iN. The resulting system of Equations (25)
is expresses in the tri-diagonal NN-matrix form:
,
A
UB (27)
where




 
2
,
,1
,1
,,
2
2,1, 2,...,,
1,1, 2,...,1,
2
1,2,3,..., ,
2
0,1, 2,...,2,,
3,4,...,,2,
,1,2,...,.
ii i
ii i
ii i
ij ji
ii
A
RqRiN
R
ApRiN
R
ApRiN
AA iN
jNji
BRsRiN


 



 
 

 
(28)
The solution of the finite difference discretization of
the two-point linear boundary value problem can
therefore be found easily even for very small mesh sizes.
6. Numerical Examples and Discussion for
Solid Disk
Some numerical examples for the rotating variable-
thickness solid disks will be given according the
analytical and numerical solutions (0.3)

. According
to Equation (7), the following dimensionless response
characteristics
 
  
 

2
2
12 2
,
1
,, ,.
r
rr
E
uURur
b
RR rr


 





(29)
determined as per the analytical solution are compared
with those obtained by the numerical FDM solution.
The results of the present investigations for the radial
displacement u are reported in Table 1. For this
example, N = 9, 19, 39 and 79, so R has the
corresponding values 0.1, 0.05, 0.025 and 0.0125,
respectively.
If we use the Richardson extrapolation method with
0.1,0.05,0.025,R

 and 0.0125 we obtain results
listed in Table 2. The first extrapolation is

 
1
4 0.050.1
Ext ;
3
ii
i
UR UR 
 (30)
the second extrapolation is

 
2
4 0.0250.05
Ext ;
3
ii
i
UR UR 
 (31)
the third extrapolation is

 
3
4 0.01250.025
Ext ;
3
ii
i
UR UR 
 (32)
the forth extrapolation is
21
4
16 ExtExt
Ext ;
15
ii
i

 (33)
and the final extrapolation is
32
5
16 ExtExt
Ext .
15
ii
i

 (34)
All of the results of 4
Ext i and 5 Ext i are correct to
the decimal places listed. In fact, if sufficient digits are
maintained, these approximations give results that agree
with the exact solution with maximum error of
8
2.9 10

 and 8 4.8 10

, respectively at the mesh
points.

A. M. ZENKOUR ET AL. 435
The distribution of the radial displacement, radial and
circumferential stresses are presented in Figure 2. The
numerical FDM solution is compared with the analytical
solution for the rotating variable-thickness sold disk with
k = 3 and various values of n. It is clear that, the FDM
gives displacement and stresses with excellent accuracy
with the exact analytical solution. It can be seen from
Figure 2 that the FDM can describe the displacement
and stresses through-the-thickness very well enough.
(a)
(b)
(c)
Figure 2. Dimensionless radial displacement u, radial stress
σ1 and circumferential stress σ2 for the variable-thickness
solid disk (k = 3): (a) n = 0.2, (b) n = 0.5 and (c) n = 0.8.
7. Formulation and Numerical Solution for
Annular Disk
Here we consider a thin annular disk varies continuously
in the form of a form of a general parabolic function (see
Figure 3):

01,
k
ra
hrhn ba














(35)
(a)
(b)
(c)
Figure 3. Variable-thickness annular disk profiles for (a) k
= 1.5 and n = 0.8, (b) k = 0.5 and n = 0.8 and (c) k = 2.5 and
n = 0.5.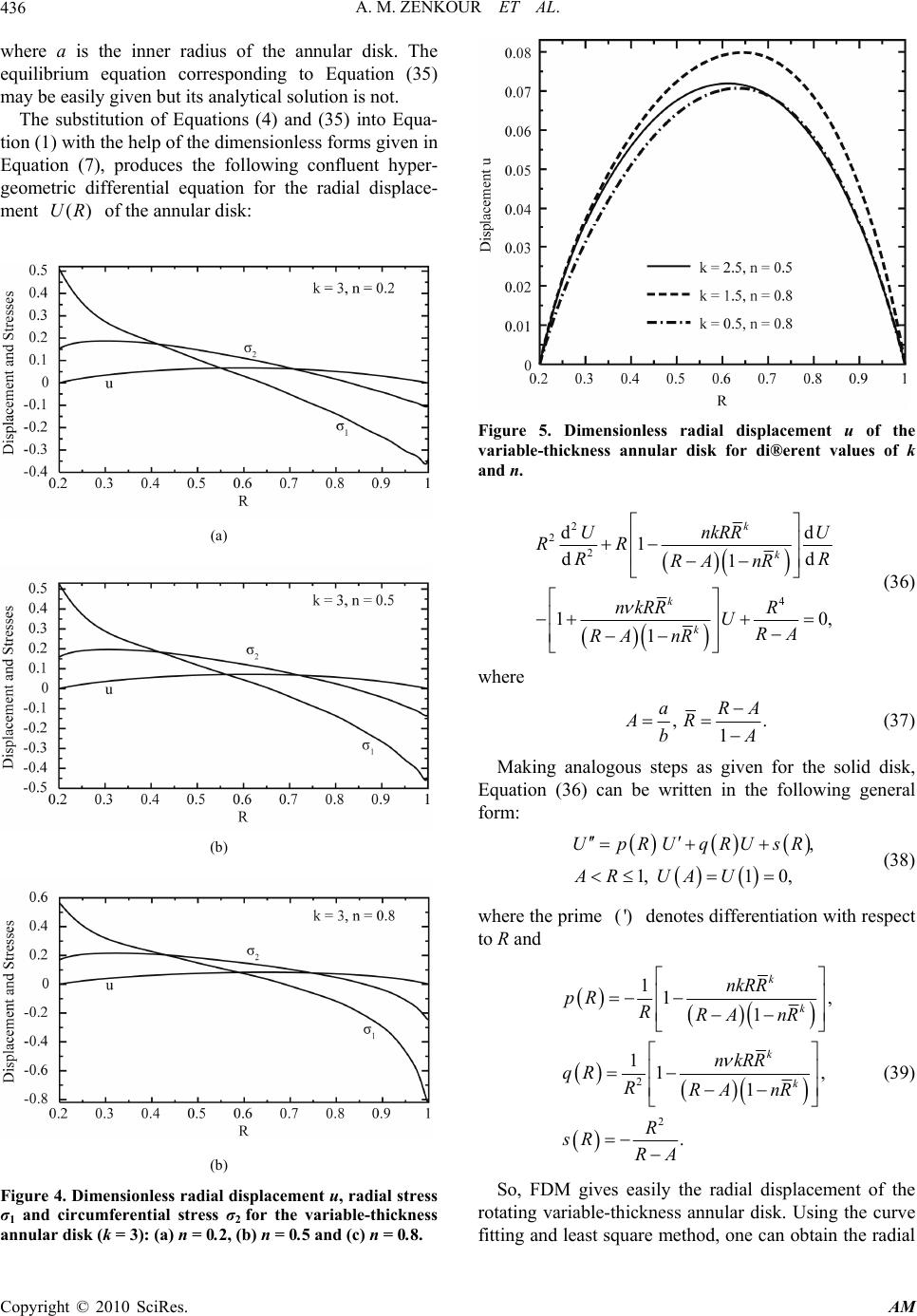

A. M. ZENKOUR ET AL. 436
where a is the inner radius of the annular disk. The
equilibrium equation corresponding to Equation (35)
may be easily given but its analytical solution is not.
The substitution of Equations (4) and (35) into Equa-
tion (1) with the help of the dimensionless forms given in
Equation (7), produces the following confluent hyper-
geometric differential equation for the radial displace-
ment ()UR of the annular disk:
(a)
(b)
(b)
Figure 4. Dimensionless radial displacement u, radial stress
σ1 and circumferential stress σ2 for the variable-thickness
annular disk (k = 3): (a) n = 0.2, (b) n = 0.5 and (c) n = 0.8.
Figure 5. Dimensionless radial displacement u of the
variable-thickness annular disk for di®erent values of k
and n.




2
2
2
4
dd
1d
d1
10,
1
k
k
k
k
UnkRRU
RR R
RRA nR
nkRRR
URA
RA nR




 









(36)
where
,.
1
aRA
AR
bA


 (37)
Making analogous steps as given for the solid disk,
Equation (36) can be written in the following general
form:


 
,
1,1 0,
UpRUqRUsR
ARUAU



 (38)
where the prime (') denotes differentiation with respect
to R and
 

 


2
2
11,
1
11,
1
.
k
k
k
k
nkRR
pR RRA nR
nkRR
qR RRAnR
R
sR RA





 















 
(39)
So, FDM gives easily the radial displacement of the
rotating variable-thickness annular disk. Using the curve
fitting and least square method, one can obtain the radial

A. M. ZENKOUR ET AL. 437
and circumferential stresses. Taking n = 0.2, 0.5 and 0.8,
and k = 0.5, 1.5, 2.5 and 3 in the variable thickness
function given in Equation (35), a rotating annular disk
with such variable thickness is studied. The inner and
outer radii of the disk are taken to be a = 0.2 b (R = A =
0.2) and b (R = 1), and the results are given in terms of
the rotating angular velocity. The results calculated with
the FDM for displacement and stresses of a rotating
variable-thickness annular disk are given in Figures 3-7.
8. Conclusions
This paper presents a unified numerical method for the
Figure 6. Dimensionless radial stress σ1 in the variable-
thickness annular disk for different values of k and n.
Figure 7. Dimensionless circumferential stress σ2 in the
variable-thickness annular disk for di®erent values of k
and n.
elastic calculation of rotating disks with a general, arbi-
trary configuration. The governing equation was derived
from the equilibrium equation and the stress- strain
relationship. The analytical solution was given for the
rotating variable-thickness solid disk. The calculation of
the rotating sold and annular disks was turned into
finding the solution of a second-order differential equa-
tion under the given conditions at two boundary fixed
points. Finite difference method algorithm was intro-
duced to solve the governing equation for both solid and
annular disks and a number of numerical examples were
studied. The results from the analytical and FDM
solutions were compared. The proposed FDM approach
gives very agreeable results to the analytical solution.
9. Acknowledgements
The investigators would like to express their appreciation
to the Deanship of Scientific Research at King
AbdulAziz University for its financial support of this
study, Grant No. ع/168/428.
10. References
[1] S. P. Timoshenko and J. N. Goodier, “Theory of Elastic-
ity,” McGraw-Hill, New York, 1970.
[2] S. C. Ugral and S. K. Fenster, “Advanced Strength and
Applied Elasticity,” Elsevier, New York, 1987.
[3] U. Gamer, “Tresca’s Yield Condition and the Rotating
Disk,” ASME Journal of Applied Mechanics, Vol. 50, No.
2, 1983, pp. 676-678.
[4] U. Gamer, “Elastic-Plastic Deformation of the Rotating
Solid Disk,” Ingenieur-Archiv, Vol. 45, No. 4, 1984, pp.
345-354.
[5] A. M. Zenkour, “Analytical Solutions for Rotating Ex-
ponentially-Graded Annular Disks with Various Bound-
ary Conditions,” International Journal of Structural Sta-
bility and Dynamics, Vol. 5, No. 4, 2005, pp. 557-577.
[6] U. Güven, “Elastic-Plastic Stresses in a Rotating Annular
Disk of Variable Thickness and Variable Density,” In-
ternational Journal of Mechanical Sciences, Vol. 34, No.
2, 1992, pp. 133-138.
[7] U. Güven, “On the Stress in the Elastic-Plastic Annular
Disk of Variable Thickness under External Pressure,” In-
ternational Journal of Solids and Structures, Vol. 30, No.
5, 1993, pp. 651-658.
[8] U. Güven, “Stress Distribution in a Linear Hardening
Annular Disk of Variable Thickness Subjected to Exter-
nal Pressure,” International Journal of Mechanical Sci-
ences, Vol. 40, No. 6, 1998, pp. 589-601.
[9] U. Güven, “Elastic-Plastic Stresses Distribution in a Ro-
tating Hyperbolic Disk with Rigid Inclusion,” Interna-
tional Journal of Mechanical Sciences, Vol. 40, No. 1,
1998, pp. 97-109.

A. M. ZENKOUR ET AL. 438
[10] A. N. Eraslan, “Inelastic Deformation of Rotating Vari-
able Thickness Solid Disks by Tresca and Von Mises Cri-
teria,” International Journal for Computational Me-
thods in Engineering Science, Vol. 3, 2000, pp. 89-101.
[11] A. N. Eraslan and Y. Orcan, “On the Rotating Elas-
tic-Plastic Solid Disks of Variable Thickness Having
Concave Profiles,” International Journal of Mechanical
Sciences, Vol. 44, No. 7, 2002, pp. 1445-1466.
[12] A. N. Eraslan, “Stress Distributions in Elastic-Plastic
Rotating Disks with Elliptical Thickness Profiles Using
Tresca and von Mises Criteria,” Zurich Alternative Asset
Management, Vol. 85, 2005, pp. 252-266.
[13] A. M. Zenkour and M. N. M. Allam, “On the Rotating
Fiber-Reinforced Viscoelastic Composite Solid and An-
nular Disks of Variable Thickness,” International Journal
for Computational Methods in Engineering Science and
Mechanics, Vol. 7, No. 1, 2006, pp. 21-31.
[14] A. M. Zenkour, “Thermoelastic Solutions for Annular Disks
with Arbitrary Variable Thickness,” Structural Engineering
and Mechanics, Vol. 24, No. 5, 2006, pp. 515-528.
[15] O. C. Zienkiewicz, “The Finite Element Method in Engi-
neering Science,” McGraw-Hill, London, 1971.
[16] P. K. Banerjee and R. Butterfield, “Boundary Element
Methods in Engineering Science,” McGraw-Hill, New
York, 1981.
[17] L. H. You, Y. Y. Tang, J. J. Zhang and C. Y. Zheng,
“Numerical Analysis of Elastic-Plastic Rotating Disks
with Arbitrary Variable Thickness and Density,” Interna-
tional Journal of Solids and Structures, Vol. 37, No. 52,
2000, pp. 7809-7820.