Communications and Network, 2010, 2, 221-229
doi:10.4236/cn.2010.24032 Published Online November 2010 (http://www.SciRP.org/journal/cn)
Optimal Spacing Design for Pilots in OFDM Systems
over Multipath Fading Channels
Youssefi My Abdelkader, El Abbadi Jamal
Laboratoire d’Electronique et Communication, EMI-Rabat, Morocco
Received July 21, 2010; revised August 31, 2010; accepted September 29, 2010
Abstract
In wireless orthogonal frequency division multiplexing (OFDM) systems, the time-varying channel is often
estimated by algorithms based on pilot symbols. Such an estimator, however, requires statistical prior
knowledge that is not easily obtained. Therefore, the pilot tones have to be close enough to fulfill the sam-
pling theorem. In this case the statistical knowledge of the channel is not required to reconstruct correctly the
channel impulse response (CIR). This paper explores the optimal placement and number of pilot symbols, we
investigate optimal training sequences in OFDM systems and we analyze the number of pilot symbols re-
quired to fulfill the sampling theorem. Using a general model for a multipath slowly fading channel, the ap-
proach is based on the LS as a criterion of channel estimation while the channel interpolation is done using
the piecewise-constant interpolation compromising between complexity and performance. Simulation results
demonstrate the good performance of our approach.
Keywords: OFDM, Multipath Channel, Channel Estimation, Pilot Symbols
1. Introduction
OFDM (Orthogonal Frequency Division Multiplexing)
has been widely applied in wireless communication sys-
tems due to its high data rate transmission and its ro-
bustness to multipath channel delay [1,2]. The channel
characteristics must be known at the receiver to recover
the transmitted signal after demodulation, so channel
estimation is needed.
Two classes of methods are available for the receiver
to acquire channel state information (CSI): One is based
on training symbols that are a priori known to the re-
ceiver, whereas the other relies only on the received
symbols to acquire CSI blindly.
Relative to training, blind schemes typically require
longer data records and entail higher complexity.
In OFDM systems, channel estimation is usually per-
formed by sending training pilot symbols on sub-carriers
known at the receiver. The quality of the estimation de-
pends on the pilot arrangement. The channel estimation
can be performed by either inserting pilot tones into all
of the subcarriers of OFDM symbols with a specific pe-
riod (Block-type) or inserting pilot tones into each
OFDM symbol (Comb-type) [3]:
1) Block-type Arrangement (shows in Figure1a):
The block type pilot channel estimation, has been devel-
oped under the assumption of slow fading channel, this
assumes that the channel transfer function is not chang-
ing very rapidly. In block-type pilot based channel esti-
mation, OFDM channel estimation symbols are trans-
mitted periodically, in which all sub-carriers are used as
pilots. If the channel is constant during the block, there
will be no channel estimation error since the pilots are
sent at all carriers. The estimation can be performed by
using either LS or MMSE.
2) Comb-type Arrangement (shows in Figure1b):
the comb-type pilot channel estimation has been intro-
duced to satisfy the need for equalizing when the channel
changes even in one OFDM block. The comb-type pilot
channel estimation consists of algorithms to estimate the
channel at pilot frequencies and to interpolate the chan-
nel.
This work is based on a Comb-type arrangement,
Comb-type pilot pattern is more appropriate for the esti-
mation of time varying channels [4]. The channel is con-
sidered to be frequency-selective invariant over each
received block, but is allowed to vary from block-to-
block.
The design of a channel estimator is based on two fun-
damental problems:

222 Y. M. ABDELKADER ET AL.
(a)
Block-type pilot arrangement
(b)
Comb-type pilot arrangement
Figure 1. Pilot arrangement
• The amount of pilot symbols to be transmitted.
• The complexity of the estimator.
The MMSE estimator has good performance but high
complexity. The LS estimator has low complexity, but its
performance is not as good as that of the MMSE estima-
tor [5]. This work is based on the LS as a criterion of
channel estimation because LS and MMSE criteria ex-
hibit similar performance in high SNR regimes. The
OFDM transmission technique is robust to multi-path
channel delay, cyclic prefix extension is used to elimi-
nate inter-symbol interference (ISI), but the Inter-carrier
interference (ICI) remains a problem because of Doppler
frequency. In fast fading channels when the channel
changes even in one OFDM block, orthogonality of the
tones can’t be preserved because of Doppler Effect [6].
Studying the optimum spacing of the pilots in the general
case shows that the optimum time-frequency spacing
depends upon the channel parameters (the Doppler fre-
quency and the power delay of the channel) [7]. There-
fore, the OFDM technique is extremely attractive for
slowly fading multipath channel as that usually used in
WLAN systems or in indoor environment.
In this paper we study the case of multipath slowly
fading channels while the orthogonality of tones is pre-
served. The optimal spacing of pilot symbols for OFDM
systems has been investigated by several studies over the
past ten years. In literature, the results of work based on
channel capacity investigating this optimization problem
[8] confirm the results of the study based on the OFDM
linear system (Y = HX+N), these studies show that in a
multipath channel with L independent paths channel es-
timation requires at least L pilot symbols equally- spaced
in the OFDM block.
In this work we explore the optimization of pilot sub-
carriers required for channel estimation and optimal po-
sitions of pilots. We show that the application of sam-
pling theorem confirms the result of previous works.
In Section 2, we describe the channel estimation based
on a Comb-type arrangement. Section 3 discusses the
optimal placement and number of pilot symbols in an
OFDM frame. Simulation results are presented in Sec-
tion 4.
2. OFDM Channel Estimation Based on
Comb-Type Pilot Arrangement
2.1. Notations
Standard notations are used in this paper.

.t Transpose
(.)

Hermitian

.

Estimate of


.



.
p
l Vector with pilot tone subscripts


.E Expectation operator


.tr Trace operator
. Absolute value
. 2-norm
In n x n Identity matrix
N Number of OFDM tones
T sThe sampling interval
T The OFDM block duration (T=N.Ts )
L Maximum length of channel
K Frequency subscript (tone number)
m Time subscript (OFDM symbol number)
Yk,m Received signal
Xk,m Transmitted data
hm Channel impulse response
Hm Channel matrix
N k,m AWGN noise
Fd Doppler frequency
2/
j
N
N
We
 

2.2. Channel Estimation Based on Comb-Type
Pilot Arrangement
In an OFDM system, the received signal at the kth tone
can be expressed as








YkHkXk IkNk

, k=0,1,…N-1
where I (k) the inter-carrier interference (ICI) because of
Doppler frequency.

Y. M. ABDELKADER ET AL.
223
,
In the case of multipath slowly fading channels, when
the channel is frequency-selective invariant over each
received block OFDM symbol, the orthogonality be-
tween subcarriers can be fully preserved, and we can
write
,,,kmkm kmkm
YHXN
There are several criteria used for channel estimation,
for reasons of complexity, the estimation can be per-
formed by using either linear MMSE criterion (Wiener
filtering) [9,10] and LS criterion. However, in high SNR
regimes and when the noise level is low, LS criterion
offers a good compromising performance / complexity.
1) The estimate of the channel at pilot sub-carriers
based on LS estimation is given as follows,
Assume that each OFDM symbol has N subcarriers
where pilots occupy p subcarriers. By LS estimation, the
channel state information (CSI) at pilot tones in the kth
OFDM symbol can be obtained as
,
,
,
ˆkm
km
km
Y
HX 
where k is the pilot tones,


12
, ...,
p
kkk k
2) Interpolation
In comb-type pilot based channel estimation, an inter-
polation technique is necessary in order to estimate
channel at data sub-carriers by using the channel infor-
mation at pilot sub-carriers [11]. The channel interpola-
tion is done using the piecewise-constant interpolation,
linear interpolation, second order interpolation, low-pass
interpolation, spline cubic interpolation…In the follow-
ing Figure 2, there’s a comparison between three types
of frequency channel response, Indoor A, Pedestrian B
and Vehicular B [12]:
The pilot symbols have to be close enough to fulfill
the sampling theorem and avoid aliasing. Therefore, with
the piecewise-constant interpolation we can reconstruct
correctly the channel impulse response as it will be
shown in this paper. Whereas, when we have enough
information about channel characteristics, we can choose
a type of interpolation to estimate the channel (even if
Figure 2. Rayleigh model 2GHz, ETSI TR101-102.
pilot symbols aren’t close enough to fulfill the sampling
theorem).
The channel estimation

e
H
k at the data-carrier
k( = 0,1, …,N-1) is given as follows,
a)


e
H
k at pilot tones is used to find the estimated
transmitted signal


e
X
k, we can get




e
e
Yk
Xk
H
k
,

12
, ...,
p
kkk k
Figure 3


e
X
k is mapped to the constellation and
then obtained


pure
X
k.
b) The estimated channel


e
X
k at pilot tones is
updated:




e
pure
Yk
Hk
X
k
, k=0,1…,N-1
The channel estimation

e
H
k at the data-carrier k


0.1, ...,1kN

 is given using an efficient interpola-
tion technique in order to estimate channel at data
sub-carriers by using the channel information at pilot
sub-carriers.
3. The Minimum Number of Pilot Tones
In this section, we present some answers to the question
of minimum number of pilots needed for channel estima-
tion in OFDM systems. This problem has been the sub-
ject of several investigations, the theoretical study shows
that the channel estimation requires at least L pilot sym-
bols, and we can prove this result by two different
methods. One is based on the sampling theorem, whereas
the other relies only on the study of the OFDM linear
system Y = HX+N.
3.1. The Application of Shannon’s Sampling
Theorem
The channel estimation with a Comb-type pilot arrange-
ment is based on an insertion of constant values called
pilots in some sub-carriers of the OFDM frame. Figure
4.
After the signal demodulation, an LS estimator gives
Figure 3. Constellation.

Y. M. ABDELKADER ET AL.
224
Figure 4. Pilot insertion.
Figure 5. Sampling process.
channel estimation at pilot sub-carriers. The piecewise-
constant interpolation is used in order to estimate chan-
nel at the values between the pilot samples as it’s shown
in Figure 5.
Therefore, the process of channel estimation based on
pilot symbols with piecewise constant interpolation is
similar to the sampling process. The BER can be lowered
by placing the pilot symbols closer than that specified by
the sampling theorem.
 Multipath channel modeling
The complexity of an estimator depends on the num-
ber of the propagation paths (determined by the ratio
between the maximum delay spread τ max and the sam-
pling period Ts). For example, in BRAN A channel
there’s 8 paths (the propagation channel for an office
environment as part of the standard HiperLAN2-5Ghz).
In the analogue domain, the multipath channel is de-
scribed by the following complex-valued impulse re-
sponse [13]:
  
1
,()
L
ll
l
htt t 



where αl is the complex gain of the lth path, τl is the
propagation delay for the lth path. In digital transmission
systems, symbols are often transmitted in regular time
interval Ts, called the sampling period. This period is
often small in comparison with the maximum delay time
τ max.
The discrete multipath model is regarded as a refer-
ence for most of the contemporary wideband terrestrial
wireless systems under a reasonable approximation of
constant number of multipath components L and slow
variation of the delay values . The multipath
channel is then modeled as

lt

  
1
,.
L
ll
l
htt T 


s
The path gains are given as samples taken at different
period Ts (see Figure 5).
 The application of sampling theorem
The spectrum of a discrete signal is a periodic signal
(see Figure 6). We will explore the duality of the Fourier
transform then we can apply the sampling theorem on the
frequency response of the channel.
Since the inter-carrier spacing is Δf and the duration of
an OFDM symbol is T=N.Ts, we have 11
s
fTNT  
If we assume that pilots are placed Nf subcarriers apart
in every OFDM symbols (Comb-type pilot arrangement),
and the pilot symbols are equally-spaced and the spacing
Figure 6. Typical multipath channel response.

Y. M. ABDELKADER ET AL.
225
between two consecutive pilot symbols is equal to e
f
,
we have
f
ef
s
N
fNf
NT

Figure 7. Structure of pilot symbols for Nf =4
Let He(f) the frequency response of the channel con-
structed from the pilot symbols with a piecewise con-
stant-interpolation.
 
 
ee
n
e
n

e
H
fHnffn
Hff nf










f
The inverse Fourier transform of this distribution is he
(t):
 


1
1
*
1
ee
n
n
ee
n
ee
ee
n
htht TFf nf
n
ht t
ff
n
ht
ff
ThtnT












 















The inverse Fourier transform of this distribution is he
(t):
 



1
1
*
1
ee
n
n
ee
n
ee
ee
n
htht TFf nf
n
ht t
ff
n
ht
ff
ThtnT












 
















Then we can reconstruct h (t) from he (t). We need a
time-domain windowing to reconstruct the time-domain
channel impulse response (CIR).
The samples have to be close enough to fulfill the
sampling theorem and avoid aliasing. So, we must
choose the sampling period Te greater than the channel
impulse response length.
Let hm=[h0,m,h1,m,…,hL-1,m]t the channel impulse re-
sponse.
The length of the multipath channel impulse response
is L.Ts. To avoid aliasing, we must respect the following
inequality . .
es
TLT
Knowing that
f
ef
s
N
fNf
NT

we have .
s
e
f
NT
TN 
however, we have the following inequality
..
s
s
f
NT LT
N 
f
NL
N
We will show later that the equispaced pilot symbols
are optimal in the sense of MMSE.
Because equispaced placement of pilot symbols is im-
possible when N / Nf is not an integer, we will consider
only the case when N / Nf is an integer.
For this special case we have
__ _
f
N
NumberofPilot TonesL
N

knowing that
f
N
Nis the number of pilot symbols in the
OFDM frame, then the channel estimation requires at
least L pilot symbols.
3.2. OFDM Linear System Y = HX+N
In the OFDM system when orthogonality is preserved,
the system equations can be expressed as
,,,kmkm kmkm
YHX N
,

 (1)
where AWGN noise.
,km
N
Let


12
,...,,
L
kkk be the set of L tones used for
transmitting pilot symbols.
In the absence of noise, from (1) we can write:
plpl pl
YHX

(2)
where
h
WW
WW
WW
N
H
Q
Lk
N
k
N
Lk
N
k
N
Lk
N
k
N
pl
LL



















)1(
)1(
)1(
...1
............
...1
...1
122
11
(3)
Since Q is a Vandermonde matrix with L parameters
distinct, h can be found exactly by inverting Q.
With the system equations (1), we have L unknowns
h1, ... hL
- If the number of pilot symbols is equal to L, then the

226 Y. M. ABDELKADER ET AL.
number of equations equals the number of unknowns,
then the system can be solved.
- If the number of pilot symbols is less than L, the
number of equations is less than the number of un-
knowns then we have an under-determined system of
linear equations [14], and hence a non-unique solution h.
Therefore, in both cases (absence or presence of noise),
L pilot symbols are the minimum number required for
exact channel estimation.
3.3. Optimum Set of Pilot Tones
It has been found in [14,15] that in the presence of
AWGN noise, the MMSE estimate of h occurs when the
pilot symbols are equally-spaced in the OFDM frame.
Proof:
From (1) we can write:
,,
,,
,,
,0,1,...,
km km
km km
km km
YS
RHk
XX
 1 N (4)
where ,
,
,arg km
km
km jX
N
Se 
from (3) we have
.
pl
H
Qh (5)
from (4,5) the MMSE estimate of h is given by:
 
1
p
lp
hQ R

l

(6)
Knowing that each pilot ,km
X
carries data of con-
stant modulus,km x X

, from (4) and (6) we have:
 
11 pl pl
x
hhQ S





11
()
,..., ,,...,
L
t
pl pl
kk kk
RRRSSS



L
t


The matrix depends on the choice of the set of
pilot tones. Thus, the design problem is to choose the set
that minimizes the MSE

pl
Q



2
Ehh.This can be ob-
tained as follows,

*1)pl(
L
s
21)pl(
x
2QIQtr
1
hhE  










2
()* ()1
()
pl pl
s
x
tr QQ




 
*
p
lpl
QQ can be expressed as
where
 

2
* pl plL
tr QQN 
Let λ1, λ2,…, λL the eigenvalues of
 

1
*pl pl
QQ

,
then the eigenvalues of
 


1
*pl pl
QQ

are 1/ λ1,1/ λ2,…,1/
λL.
Since the trace of a matrix is the sum of its eigenval-
ues, hence, the relaxed optimization problem is
1
mini mize
L
p
p


 (7)
2
1
1
L
pp
L
Where N



.
Since the matrix
 


1
*pl pl
QQ

is non-negative-
definite, all the eigenvalues are non-negative. So, the
minimization occurs if all the eigenvalues λi (i=1,..,L )
are identical. This occurs if:
 
*pl pl
L
L
QQ I
N

Therefore, the optimal sets of tones are

1
,,..., LN
N
iii
LL











,
where 0,1,..., 1
N
iL

.
4. Simulation Results
4.1. Effect of Multipath Channel
To validate our analysis, we test an OFDM 16 QAM
transmission over a multipath channel in the absence of
noise (4 paths, 6 paths and 10 paths) with N=256 subcar-
riers, and cyclic prefix length equal to CP=32.
In all the following simulations we have chosen the
cyclic prefix to be greater than the maximum delay spread
in order to avoid inter-symbol interference (shows in
Figure 7).
In Figure. 9 we can see clearly the effect of multipath
channel; we notice that as the multipath channel length
increases, the error rate increases. Channel estimation is
necessary to correct the OFDM symbols.
Figure 8. 16-QAM constellation.

Y. M. ABDELKADER ET AL.
227
4.3. Optimal Spacing of Pilot Symbols
We consider a typical OFDM system, where N=256
subcarriers, and cyclic prefix length equal to CP=32 and
64 QAM transmission over a multipath channel. We also
Figure 9. Effec t of multipath channel.
4.2. Channel Estimation Based on Pilot Symbols
We consider a typical OFDM system, where N=256
subcarriers, and cyclic prefix length equal to CP=32 and
16 QAM transmission over a multipath channel in the
absence of noise (8 paths). Figure 10. Signal constellation before correction.
We also insert equally-spaced pilot symbols (1 + j),
the receiver uses an LS estimator and interpolation. We
deal with two cases:
1) We insert 16 pilot symbols in every OFDM frame,
then the number of pilot symbols is greater than the
channel length (L=8 paths).
2) We insert 8 pilot symbols in every OFDM frame,
then the number of pilots is equal to the channel length
(L=8 paths).
The simulation results are shown in Figure 10 and
Figure 11.
We notice that the channel estimation with 16 pilot
symbols /OFDM frame have good performance as it is
shown in the Figure11. Otherwise, using 8 pilots/OFDM Figure 11. Constellation after correction.
Figure 12. BER versus pilot spacing (4 paths).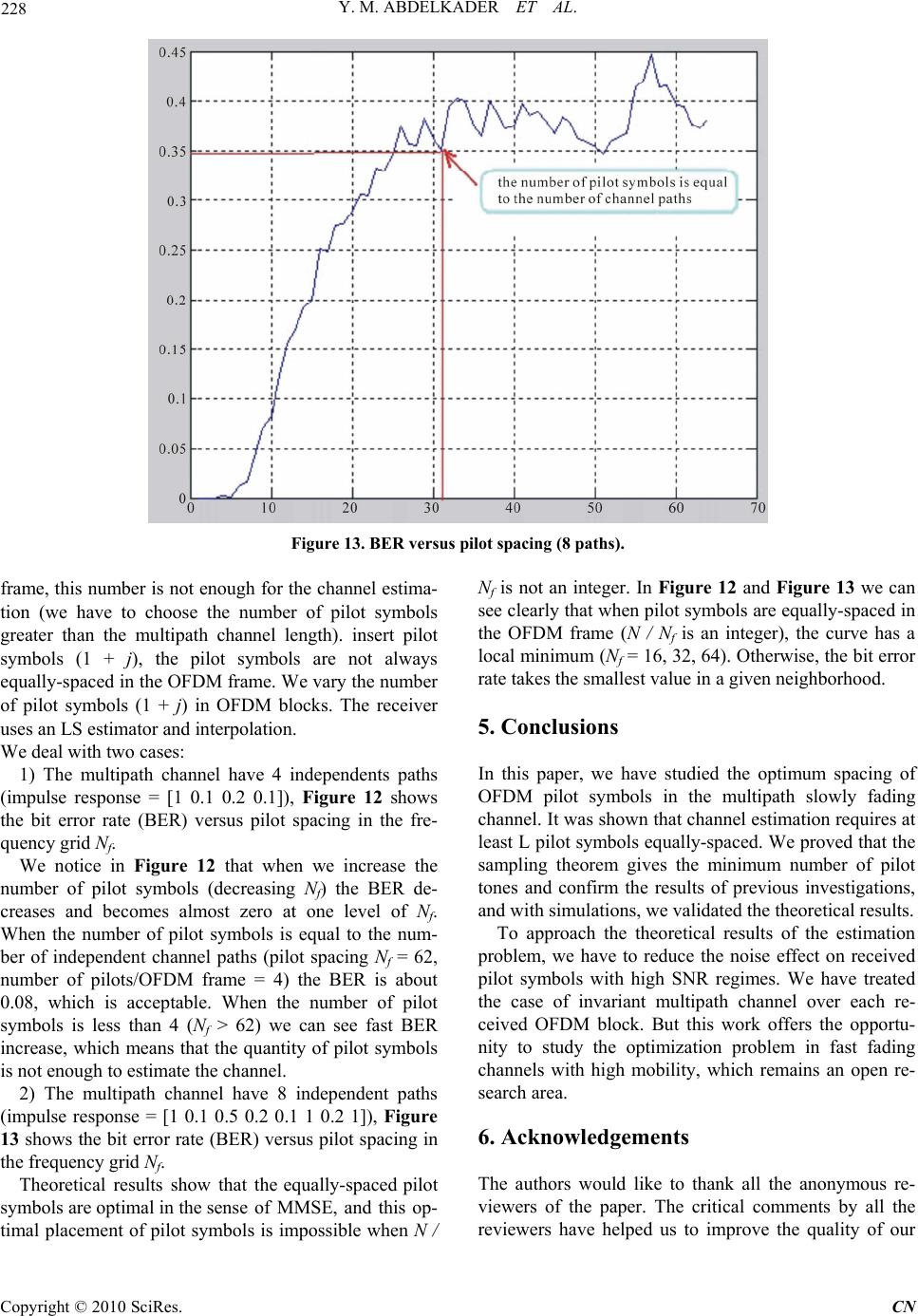

228 Y. M. ABDELKADER ET AL.
Figure 13. BER versus pilot spacing (8 paths).
frame, this number is not enough for the channel estima-
tion (we have to choose the number of pilot symbols
greater than the multipath channel length). insert pilot
symbols (1 + j), the pilot symbols are not always
equally-spaced in the OFDM frame. We vary the number
of pilot symbols (1 + j) in OFDM blocks. The receiver
uses an LS estimator and interpolation.
We deal with two cases:
1) The multipath channel have 4 independents paths
(impulse response = [1 0.1 0.2 0.1]), Figure 12 shows
the bit error rate (BER) versus pilot spacing in the fre-
quency grid Nf.
We notice in Figure 12 that when we increase the
number of pilot symbols (decreasing Nf) the BER de-
creases and becomes almost zero at one level of Nf.
When the number of pilot symbols is equal to the num-
ber of independent channel paths (pilot spacing Nf = 62,
number of pilots/OFDM frame = 4) the BER is about
0.08, which is acceptable. When the number of pilot
symbols is less than 4 (Nf > 62) we can see fast BER
increase, which means that the quantity of pilot symbols
is not enough to estimate the channel.
2) The multipath channel have 8 independent paths
(impulse response = [1 0.1 0.5 0.2 0.1 1 0.2 1]), Figure
13 shows the bit error rate (BER) versus pilot spacing in
the frequency grid Nf.
Theoretical results show that the equally-spaced pilot
symbols are optimal in the sense of MMSE, and this op-
timal placement of pilot symbols is impossible when N /
Nf is not an integer. In Figure 12 and Figure 13 we can
see clearly that when pilot symbols are equally-spaced in
the OFDM frame (N / Nf is an integer), the curve has a
local minimum (Nf = 16, 32, 64). Otherwise, the bit error
rate takes the smallest value in a given neighborhood.
5. Conclusions
In this paper, we have studied the optimum spacing of
OFDM pilot symbols in the multipath slowly fading
channel. It was shown that channel estimation requires at
least L pilot symbols equally-spaced. We proved that the
sampling theorem gives the minimum number of pilot
tones and confirm the results of previous investigations,
and with simulations, we validated the theoretical results.
To approach the theoretical results of the estimation
problem, we have to reduce the noise effect on received
pilot symbols with high SNR regimes. We have treated
the case of invariant multipath channel over each re-
ceived OFDM block. But this work offers the opportu-
nity to study the optimization problem in fast fading
channels with high mobility, which remains an open re-
search area.
6. Acknowledgements
The authors would like to thank all the anonymous re-
viewers of the paper. The critical comments by all the
reviewers have helped us to improve the quality of our

Y. M. ABDELKADER ET AL.
229
paper.
7. References
[1] M. Engels, “Wireless OFDM Systems,” Kluwer Aca-
demic Publishers, New York, 2002.
[2] R. S. B. Ahmad and R. S. Burton, “Multi-Car-
rier_Digital_Communications: Theory and Applications
of OFDM,” Kluwer Academic Publishers, New York,
2002.
[3] M. S. Akram, “Pilot-based Channel Estimation in OFDM
Systems,” Master Dissertation, Technical University of
Denmark, Denmark, 2007.
[4] S. Coleri, M. Ergen, A. Puri and A. Bahai, “Channel Es-
timation Techniques Based on Pilot Arrangement in
OFDM Systems,” IEEE Transactions on, Vol. 48, No. 3,
September 2002, pp. 223-229.
[5] J. J. van de Beek, O. Edfors, M. Sandell, S. K. Wilson, W.
Per and P. O. Börjesson, “On Channel Estimation in
OFDM Systems,” Vehicular Technology Conference,
IEEE 45th, Vol. 2, 1995, pp. 815-819.
[6] H. Hijazi and L. Ros, “Rayleigh Time-varying Channel
Complex Gains Estimation and ICI Cancellation in
OFDM Systems,” European Transactions on Telecom-
munications, Vol. 20, No. 1, 2009, pp. 782-796.
[7] R. Gonzalez and F. bader, “Time-Frequency Spacing
Design for PACE in OFDM Systems,” 14th IST Mobile
and Wireless Communications Summit, Dresden, 2005.
[8] S. Ohno and G. B. Giannakis, “Capacity Maximizing
MMSE-Optimal Pilots for Wireless OFDM over Fre-
quency-Selective Block Rayleigh Fading Channels,”
IEEE Transactions on Information Theory, Vol. 50, No. 9,
2004, pp.2138-2145.
[9] P. Hoeher, S. Kaiser and P. Robertson, “Pi-
lot-Symbol-Aided Channel Estimation in Time and Fre-
quency,” Kluwer Academic Publishers, USA, 1997.
[10] M. Sandell and O. Edfors, “A Comparative Study of Pi-
lot-Based Channel Estimators for Wireless OFDM,” Di-
vision of Signal Processing, Luleå University of Tech-
nology, Luleå, Sweden, September 1996.
[11] P. Y. Tsai and T. D. Chiueh, “Frequency-Domain Inter-
polation Based Channel Estimation in Pilot-Aided OFDM
Systems,” Vehicular Technology Conference, IEEE 59th,
Vol. 1, 2004, pp. 420-424.
[12] L. Ros, “Réception multi-capteur pour un terminal
radio-mobile dans un système d’accès multiple à
répartition par codes,” INP Grenoble, 2001.
[13] D. Tse and P. Viswanath, “Fundamentals of Wireless
Communication,” Cambrige University Press, UK, 2005.
[14] R. Negi and J. Cioffi, “Pilote Tone Selection for Channel
Estimation in a Mobile OFDM System,” Consumer Elec-
tronics. ICCE, Stanford, 1998, pp. 466-467.
[15] X. D. Cai and G. B. Giannakis “Error Probability
Minimizing Pilots for OFDM with M-PSK Modula-
tion over Rayleigh-Fading Channels,” IEEE Trans-
actions, Vol. 53, No. 1, 2004, pp. 145-160.