Communications and Network, 2010, 2, 216-220
doi:10.4236/cn.2010.24031 Published Online November 2010 (http://www.SciRP.org/journal/cn)
Locating Mobile Users Using Base Stations of
Cellular Networks
Ilya M. Averin, Victor T. Ermolayev, Alexander G. Flaksman
Wireless Technologies Department, Mera NN, Russia
Received July 14, 201 0; revised August 31, 2010; accepted September 29, 2010
Abstract
The location of mobile users served by cellular networks is considered. The chosen approach assumes that
location is estimated through angular triangulation with three base stations (BSs). New estimates are pro-
posed, which are described by closed-form expressions, and are alternatives to the maximum likelihood es-
timate. It is shown that the accuracy of the estimate coin ciding with incircle center of the bearing triangle is
close to the accuracy of the maximum likelihood estimate.
Keywords: Position Location, Location-based Services, Cellular Networks
1. Introduction
There is significant interest in location technologies in
wireless networks. Information about the user position
can be used for the development of location-based ser-
vices [1] or for enhancing security [2]. The specifications
of next generation cellular networks (LTE, WiMax) as-
sume widespread implementation of spatial signal proc-
essing. This means that most BSs will be equipped with
multiple antennas. Therefore, location techniques based
on angular triangulation [3,4] are of interest for advanced
wireless networks. In [5], the angular triangulation ap-
proach applied to wireless networks is considered. It is
shown that the corresponding location accuracy satisfies
existing requirements [2]. However, only the somewhat
complex maximum likelihood algorithm is presented
there.
This paper proposes a positioning algorithm with low
computational complexity and gives some estimates of
its accuracy. The basic idea of the approach is to define a
bearing triangle using the bearings of a mobile user
measured at three BSs and then to try orthocenter, incir-
cle center and centroid of this triangle as the candidate
points of mobile user position.
The rest of the paper is organized as follows: the de-
scription of the proposed algorithm is given in Section 2,
Section 3 discusses the simulation results and Conclu-
sions are listed in Section 4.
2. Positioning by Means of Angular
Triangulation
Figure 1 shows the geometry of angular triangulation
with 3 BSs involved. The mobile is situated at the point


00
,
x
y. True bearings referenced to the BSs are
123
,,

. The same figure depicts the situation when not
true but the measured 1

, 2

and 3

bearings are
known. Due to finite accuracy of direction finding, more
than one cross point exists now and the intersections of
bearing lines cause the appearance of bearing triangle
 abc. This, in turn, makes the finding of the optimal es-
timate of the mobile’s position non-triv ial.
The bearing estimates can be introduced as independ-
ent Gaussian random values centered, of course, on the
true bearings [6]. Therefore, the likelihood function with
respect to the unknown exact angular directions
123
,,

 is written as
 
2
3
123 32
1
1
1
,,exp 2
22
ii
ii
i
i
P

 










 (1)
where i

is the standard deviation of the bearing error
measured at the BSi.
In order to derive the maximum likelihood estimate of
mobile user position , one should find the poin t where the
ikelihood function (1) reaches its extremum given three l

I. M. AVERIN ET AL.
217
Figure 1. The geometry of angular triangulation with 3 BSs.
known bearing measurements 1

, 2

and 3

. The so-
lution of this problem gives the maximum likelihood
estimate of bearings seen at the corresponding BSs.
However, as depicted by Figure 1, the true angular
123
,,

coordinates of the mobile are interdependent
values. This makes the maximum likelihood approach
quite complex from a computational point of view and an
alternative way is of interest.
The bearing triangle  abc, like any other triangle, has
such points as orthocenter, incircle center and centroid
(the cross point of altitudes, ang le bisectors and medians,
respectively) [7]. If the positions of a triangle’s vertices
are known, it is straightfo rward to find coo rdinates of the
points mentioned above using closed-form analytical
expressions.
One can show, for example, that the coordinates of in-
circle center are described by the Equation (2) where the
additional variables are introduced as Equation (3) and a,
b, c,(a
x
,a), (b y
x
,b), (c y
x
,c) are the triangle’s side
lengths and the coordinates of its vertices respectively.
y
Therefore, the coordinates of the orthocenter, incircle
center and centroid are explicitly defined by the positions
of the bearing triangle’s vertices. In turn, they are fully
dependant on three measured bearings. This allows us to
consider the orthocenter, incircle center and centroid as
simple-to-evaluate estimates o f mobile user pos ition. The
next section addresses the issue of the positioning accu-
racy that can be attained with such an approach.
3. Simulation Results
To keep consistency with [5], we considered a network
with hexagonal structure Figure 1 of four BSs (BS1 –
BS4). The structure shown corresponds to the “edge ex-
cited” network geometry, which assumes that a cell con-
sists of three sectors and the BS is located at their verti-
ces. Due to the properties of a hexagonal layout the dis-
tances between any neighboring BSs are the same and
equal to d. Hereinafter, the coordinates normalized to d
are considered. This means that the distance between any
122 112
21 12
12 2112
21 12
()()()( )()()()
()()()()
()()()()()()()
()()()()
babaA babab
IC abb a
abbaa bbbaa
IC abb a
yyxxxxyyxxx yyxxx
xyyxx yyxx
x
xyyy yy yxxyyyxxy
yyyxx yyxx


 

(2)










11 21
,,,
1111
acaccbcb
x
acxyacy xbaxybay
xyxy
acacba ba

 

(3)

I. M. AVERIN ET AL.
218
two nearest BSs is equal to 1 and any cell side has leng th
13.
One assumption we made was about the placement of
the mobile. It was assumed to be anywhere within the
northeast sector of the central cell with uniform probabil-
ity (this area is highlighted with th e gray color in Figure
1.) Another assumption concerned the BSs involved in
the location estimation process. Two scenarios were con-
sidered: the signal transmitted by the mobile was re-
ceived by three BSs - either by BS1BS2BS3 (sce-
nario 1) or by B S1BS2BS4 (scenario 2).
The task was to estimate the mobile’s position based
on the measured bearings. As position estimates are ran-
dom values, the location accuracy was convenient to
define by the CEPn metric. The CEP term stands for the
Circular Error Probability and the parameter n defines
the required probability level. In other words, the CEPn
metric is a radius of the circle comprising n% of the es-
timates obtained. The circle is centered about the true
position of the lo cated obj ect. Greater CEPn for the fixed
n means worse location accuracy. In the case that nor-
malized coordinates are used, the CEPn is a dimen-
sionless value. In order to get the absolute value of posi-
tioning error one should multiply the obtained CEPn by
the normalization factor (by BS-to-BS distance d for the
considered scenarios).
Simulations were performed to evaluate the location
accuracy of the proposed algorithm. The corresponding
results are shown in Figure 2, Figure 3 (for scenario 1)
and Figure 4, Figure 5 (for scenario 2). The curves pre-
sent the dependences of positioning error (in terms of the
dimensionless CEPn) upon the standard deviation
 of
bearing error. The value of

was assumed to be the
same for all BSs. For each value of

, 105 random po-
sitions within the north east sector of the cen tral cell were
considered. For every current position, three bearings
were generated as Gaussian random values. This set of
bearings was used to find the current estimate of mobile
user position. The distance between the true and esti-
mated positions was stored as the positioning error. The
process resulted in the set of positioning errors corre-
sponding to the estimate used and the topology of the
BSs involved. At the final stage the CEP67 and CEP95
were evaluated.
As follows from the results presented in Figure 2-5,
the usage of incircle center as the position estimate al-
lows to get better accuracy than the usage of centroid or
orthocenter. The accuracy of such an approach is close to
the accuracy obtained with the maximum likelihood
method. If the mobile is located by BS1, BS2 and BS3 the
accuracy decreases by only 5-6% compared to the per-
formance of the maximum likelihood estimate. This de-
terioration has weak dependency upon the value of bear-
ing error. For the second scenario, where the mobile is
located by BS1, BS2 and BS4 the accuracy decreases by
15-20% against the accuracy of maximum likelihood
approach. The accuracy dependence on the value of
bearing error is stronger now.
The actual requirements on location accuracy can be
found, for example, in [2]. For network-based technolo-
gies it claims to require accuracy of 100 meters for 67%
of all calls and an accuracy level of 300 meters for 95%
of all calls. Therefore, the requirements are CEP67=100
m and CEP95=300 m. Under the assumption of d=1000
m (this value of BS-to-BS distance is usual for an urban
Figure 2. CEP67 against standard deviation of bearing error for scenario 1.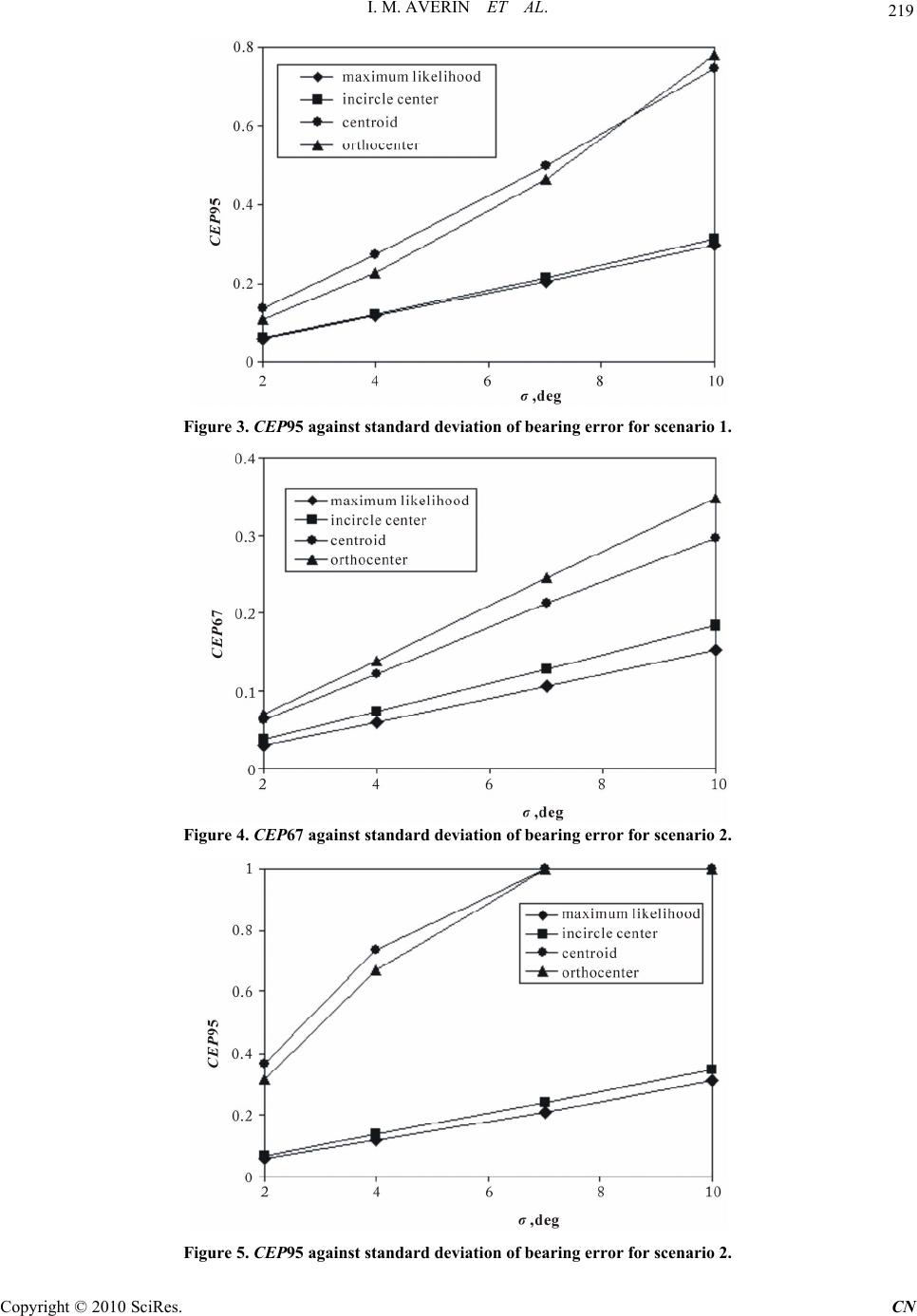

I. M. AVERIN ET AL.
219
Figure 3. CEP95 against standard deviation of bearing error for scenario 1.
Figure 4. CEP67 against standard deviation of bearing error for scenario 2.
Figure 5. CEP95 against standard deviation of bearing error for scenario 2.

I. M. AVERIN ET AL.
220
environment) and the usage of the incircle center as the
estimate, the location accuracy for the first scenario sat
isfies the requirement as long as
  6 (for CEP67) and
  9 (for CEP95). Considering the second scenario, it
is easy to see that the corresponding limit values are
 
5 (for CEP67) and
 8 (for CEP95). It should be noted
that for a smaller BS-to-BS distance, larger bearing er-
rors are acceptable.
The presented results also show that the use of cen-
troid or orthocenter as the position estimates lead s to the
greater positioning errors (compared to the incircle cen-
ter). As follows from comparison of the curves, the ac-
curacy deterioration in terms of the CEP95 is greater
than in terms of the CEP67. This means that corre-
sponding CDFs appear to have longer tails due to rare
but significant positioning errors.
4. Conclusions
An alternative approach to the maximum likelihood one
has been proposed. It involves the estimation of the mo-
bile’s position by a closed-form analytical expression.
The obtained results have demonstrated that the estimate
coinciding with the intersection point of the bearing tri-
angle’s angle bisectors (the so-called ‘incircle centre’)
has an accuracy similar to the accuracy of the maximum
likelihood estimate. Taking in to accoun t the si mplicity of
its evaluation, the ‘incircle centre’ estimate may be of
interest from a practical point of view.
Acknowledgments: The authors would like to thank
D.D.N.Bevan for support and collabora tion.
5. References
[1] J. Edwards, “TELECOSMOS: The next great telecom
revolution,” John Wiley & Sons, New York, 2005.
[2] FCC Docket No. 94-102, “In the Matter of Revision of
the Commission’s Rules to Ensure Compatibility with
Enhanced 911 Emergency Calling Systems,” Third report
and order, FCC 99-245, 1999.
[3] O. Besson, F. Vincent, P. Stoica, and A. B. Gershman,
“Approximate Maximum Likelihood Estimators for Ar-
ray Processing in Multiplicative Noise Environments,”
IEEE Transactions on Signal Processing, Vol. 48, No. 9,
2000, pp. 2506-2518.
[4] S. Valaee, B. Champagne and P. Kabal, “Parametric Lo-
calization of Distributed Sources,” IEEE Transactions on
Signal Processing, Vol. 43, No. 9, 1995, pp. 2144-2153.
[5] V. T. Ermolayev, A. G. Flak sman, D. D. N. Bevan and I.
M. Averin, “Estimation of the Mobile User Position in
the Cellular Communication System in a Multipath En-
vironment of Signal Propagation,” Radiophysics and
Quantum Electronics, Vol. 51, No. 2, 2008, pp. 145-152.
[6] D. D. N. Bevan, V. T. Ermolay ev, A. G. Flaksman and I.
M. Averin, “Gaussian Channel Model for Mobile Multi-
path Environment,” EURASIP Journal on Applied Signal
Processing, Vol. 2004, No. 9, 2004, pp. 1321-1329.
[7] http://en.wikipedia.org/wiki/Triangle