Paper Menu >>
Journal Menu >>
 Applied Mathematics, 2010, 1, 357-365 doi:10.4236/am.2010.15047 Published Online November 2010 (http://www.SciRP.org/journal/am) Copyright © 2010 SciRes. AM Study the Thermal Gradient Effect on Frequencies of a Trapezoidal Plate of Linearly Varying Thickness Arun Kumar Gupta, Pragati Sharma Department of Mathematics, M. S. College, Saharanpur, India E-mail: gupta_arunnitin@yahoo.co.in, prgt.shrm@gmail.com Received August 12, 2010; revised August 24, 2010; accepted August 27, 2010 Abstract In this paper, effect of thermal gradient on vibration of trapezoidal plate of varying thickness is studied. Thermal effect and thickness variation is taken as linearly in x-direction. Rayleigh Ritz technique is used to calculate the fundamental frequencies. The frequencies corresponding to the first two modes of vibrations are obtained for a trapezoidal plate for different values of taper constant, thermal gradient and aspect ratio. Re- sults are presented in graphical form. Keywords: Frequencies, Trapezoidal Plate, Linearly Thickness, Thermal Gradient 1. Introduction With the advancement of technology, plates of variable thickness are being extensively used in civil, electronic, mechanical, aerospace and marine engineering applica- tions. It becomes very necessary, now a day, to study the vibration behaviour of plates to avoid resonance excited by internal or external forces. A number of researchers have worked on free vibration analysis of plates of dif- ferent shapes and variable thickness. Trapezoidal plates are widely used in various structures; however, they have been poorly studied, unlike other plates. Trapezoidal plates find various applications in the construction of modern high speed air craft. The vibration characteristics of such plates are of interest to the designer. Liew and Lam [1] worked on the vibrational response of symmet- rically laminated trapezoidal composite plates with point constraints. Chopra and Durvasula [2] worked on the vibration of simply supported trapezoidal plates. Ortho- tropic plates with clamped boundary conditions were studied by Narita, Maruyama and Sonoda [3]. Liew and Lim [4] have studied the free transverse vibrational analysis of symmetric trapezoidal plates with linearly varying thickness. Qatu, Jaber and Leissa [5] have work- ed on the natural frequencies of trapezoidal plates with completely free boundaries. Qatu [6] presents the natural frequencies for laminated composite angle-ply triangular and trapezoidal plates with completely free boundaries. Bambill, Laura and Rossi [7] have studied the transverse vibrations of rectangular, trapezoidal and triangular orthotropic cantilever plates. Chen, Kitipornchai, Lim and Liew [8] have worked on the free vibration of canti- levered symmetrically laminated thick trapezoidal plates. Saliba [9-10] discussed the free vibration analysis of simply supported symmetrical trapezoidal plates as well as the transverse free vibration of fully clamped symmet- rical trapezoidal plates. Krishnan and Deshpande [11] have studied the free vibration analysis of the trapezoidal plates. Gupta et al. [12-15] have worked on the vibration analysis of visco-elastic rectangular plates of variable thickness and studied the thermal gradient effect and non-homogeneity effect on the free vibrations of the plate. Huang, Hsu and Lin [16] studied the experimental and numerical investigations for the free vibration of cantilever trapezoidal plates. Tomar and Gupta [17-18] studied the effect of thermal gradient on frequencies of orthotropic rectangular plate of variable thickness in one and two direction. As till now no authors discussed the thermally induced vibration of trapezoidal plate of variable thickness. So, in this paper the temperature effect on vibration of trape- zoidal plate of linearly varying thickness is studied. Free transverse vibrations of trapezoidal plates of varying thickness with two opposite simply supported edges have been studied on the basis of classical plate theory. In order to calculate natural frequencies for first and second mode of vibration, Rayleigh Ritz method is used. The frequencies for the first and second mode of vibration is calculated for the trapezoidal plate having C-S-C-S edges for the different values of taper constant , thermal gradi- 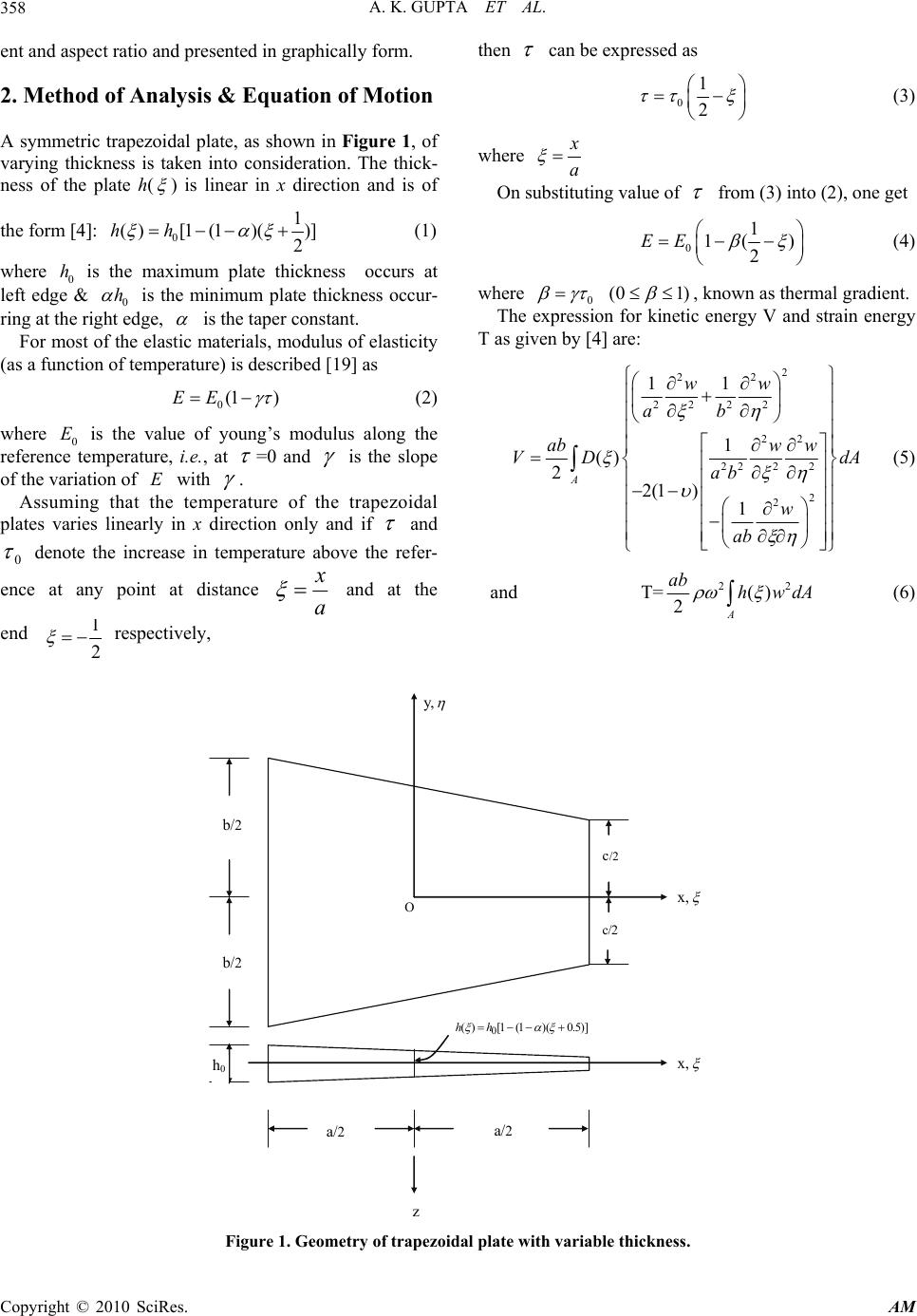 A. K. GUPTA ET AL. Copyright © 2010 SciRes. AM 358 ent and aspect ratio and presented in graphically form. 2. Method of Analysis & Equation of Motion A symmetric trapezoidal plate, as shown in Figure 1, of varying thickness is taken into consideration. The thick- ness of the plate h( ) is linear in x direction and is of the form [4]: 0 1 ( )[1(1)()] 2 hh (1) where 0 h is the maximum plate thickness occurs at left edge & 0 h is the minimum plate thickness occur- ring at the right edge, is the taper constant. For most of the elastic materials, modulus of elasticity (as a function of temperature) is described [19] as 0(1 )EE (2) where 0 E is the value of young’s modulus along the reference temperature, i.e., at =0 and is the slope of the variation of E with . Assuming that the temperature of the trapezoidal plates varies linearly in x direction only and if and 0 denote the increase in temperature above the refer- ence at any point at distance a x and at the end 1 2 respectively, then can be expressed as 0 1 2 (3) where a x On substituting value of from (3) into (2), one get 0 1 1( ) 2 EE (4) where 0 (0 1) , known as thermal gradient. The expression for kinetic energy V and strain energy T as given by [4] are: 2 22 22 22 22 22 22 2 2 11 1 () 2 2(1 ) 1 A ww ab ab ww VD dA ab w ab (5) and T= A dAwh ab 22 )( 2 (6) b/ 2 b/ 2 h 0 a/ 2 a/ 2 c/2 c/2 x, x, z y, O )]5.0)(1(1[)(0 hh Figure 1. Geometry of trapezoidal plate with variable thickness.  A. K. GUPTA ET AL. Copyright © 2010 SciRes. AM 359 in which ()D is the flexural rigidity of the plate, which is given by 3 0 1 ()1 12 DD (7) where 3 0 02 ,, 12(1 ) Eh xy D ab (8) is the flexural rigidity of the plate, is the Poisson ratio, A is the area of the plate, is the mass density per unit area of the plate and is the angular fre- quency of vibration. Using (8) and (4) in (7) 3 00 2 3 1 () [112 12(1 ) 1 1] 2 Eh D (9) Using (9) in (5) 3 00 3 11 [1 11 2 222 12(1 ) 2 22 11 22 22 ] 2 22 2 11 2(1) 22 22 A V Eh ab ww ab dA ww w ab ab (10) Using (1) in (6) 22 0 1 1(1 )() 22 A ab Th wdA (11) 3. Solution and Frequency Equations Here Rayleigh Ritz technique is used for finding the so- lution. According to this the maximum strain energy be equal to the maximum kinetic energy i.e. ()0VT (12) For the plate considered here boundaries are defined by four straight lines 1 4242 1 4242 1 2 1 2 cc bb cc bb (13) The two term deflection function taken as, 2 1 3 2 22 11 222 4 11 24 22 24 24 bc bc wA bcbc A bc bcbc bc (14) where A1 and A2 are constants. Equation (14) is taken to satisfy boundary condition and provides a good estimation to the frequency. Two edges of the plates are clamped and two are sim- ply supported i.e. all the four degree of freedoms of the nodes to the side faces of the plates are constrained. Using (13) in (10) and (11) V = 3 00 1 13 24 42 21 11 2 22 112(1 ) 1 224 42 1 12 2 22 11 22 22 2 22 2 11 2(1) 22 22 c c bb Eh ab c c bb ww ab d ww w ab ab d (15) 1 1 4242 2 22 0 11 24242 1 [1 (1)()] 22 cc bb cc bb ab Thwdd (16) Now Equation (12) becomes 2 11 ()0VT (17)  A. K. GUPTA ET AL. Copyright © 2010 SciRes. AM 360 where 1 1 3 4242 2 1 11 24242 2 22 22 22 2 22 2 22 22 1 11 22 1 12 11 11 2(1 ) cc bb cc bb ab V ww ab dd ww w ab ab (18) 1 1 4242 2 2 10 11 24242 1 [1 (1)() 2 cc bb cc bb Th wdd (19) In Equation (17), 2 00 252 2112 hE a is a frequen- cy parameter. Equation (17) involves the unknown, A1 and A2 arising due to the substitution of w from Equation (14). These unknowns are to be determined from Equation (17), for which 2 11 1 2 11 2 ()0 ()0 VT A VT A (20) On solving (20) we have 11220 mm bAbA (21) where 12 ,( 1,2) mm bb m involves parametric const. and frequency parameter. The determinant of the coefficient of (21) must vanish for a non-zero solution. Therefore the frequency equation comes out to be 11 12 21 22 0 bb bb (22) From Equation (22), a quadratic equation in 2 is obtained which gives two values of 2 . 4. Result and Discussion Frequency (22) is quadratic in2 , so it will gives two roots. The frequency is calculated for the first two mode of vibration for a c-s-c-s, trapezoidal plate with linearly varying thickness, for various values ofa/b, c/b, , and = .33. All these results are presented in graphical form. First mode of vibrations is presented in Figure (a) and second mode of vibrations is presented in Figure (b). Figures 2 and 3: In these figures different values of taper constant and different aspect ratio c/b = 1.0,0.5 and two values of thermal gradient 0.0,0.4 are taken. Figures 4 and 5: In these figures different values of thermal gradient and different aspect ratio c/b = 1.0,0.5, a/b = 1.0 and two values of taper constant 0.0,0.4 are taken. Figures 6 and 7: In these figures different aspect ratio a/b = 1.0,0.75, c/b = 1.0,0.75,0.50,0.25 and four combi- nation of thermal gradient and taper constant i.e. 0.0, 0.0;0.0, 0.4; 0.4, 0.0;0.4, 0.4 Figures 2 and 3 show that increase in taper constant makes a increase in frequency for 0.0,0.4 . Also with increase in aspect ratio c/b the frequency decreases for first two mode of vibration. 0.0 0.2 0.4 0.6 0.8 1.0 20 22 24 26 28 30 First mode c/b=1.0, a/b=1.0 =0.0 =0.4 (a) 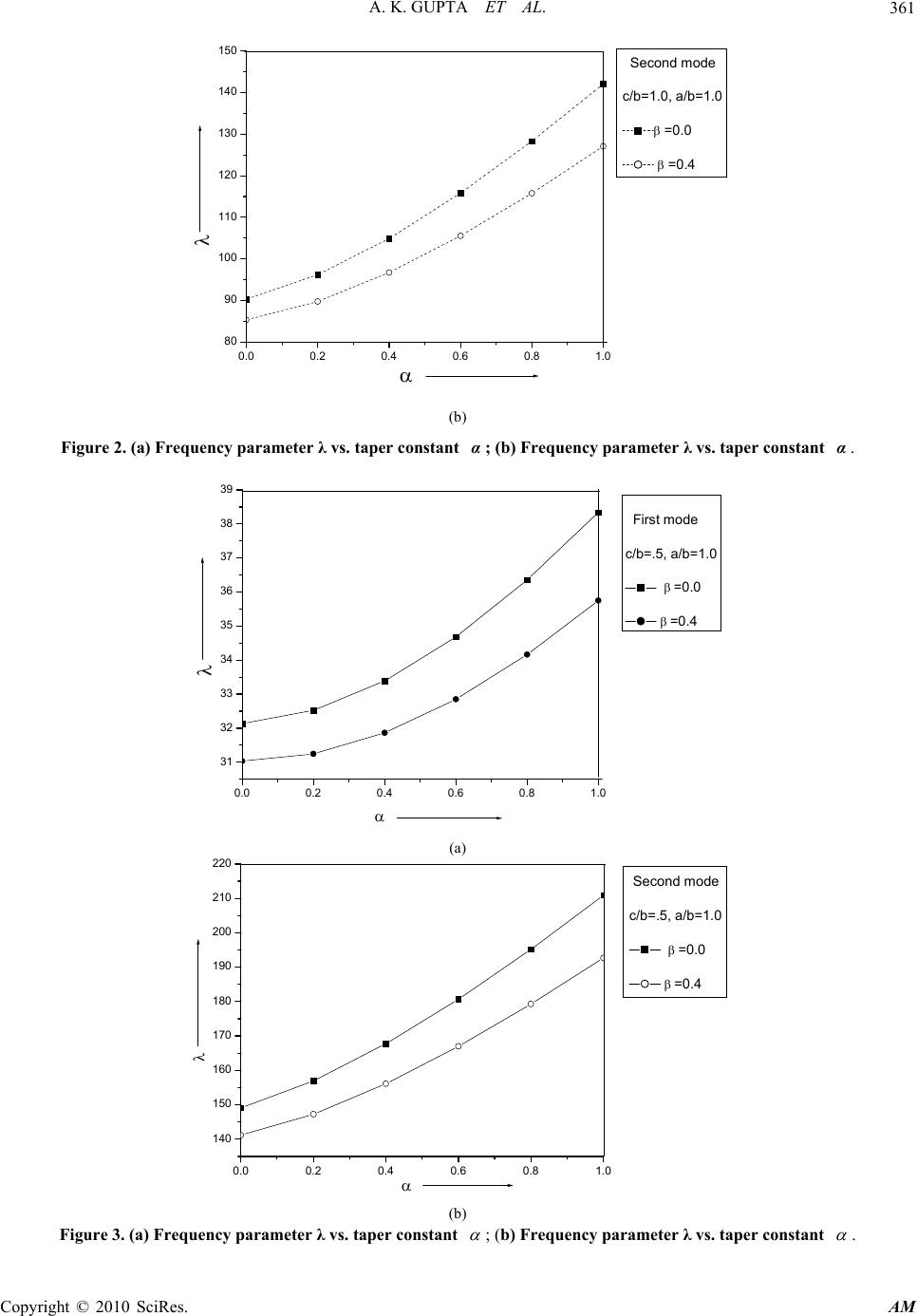 A. K. GUPTA ET AL. Copyright © 2010 SciRes. AM 361 0.0 0.2 0.4 0.6 0.8 1.0 80 90 100 110 120 130 140 150 Second mode c/b=1.0, a/b=1.0 =0.0 =0.4 (b) Figure 2. (a) Frequency parameter λ vs. taper constant α; (b) Frequency parameter λ vs. taper constant α. 0.0 0.2 0.4 0.6 0.8 1.0 31 32 33 34 35 36 37 38 39 First mode c/b=.5, a/b=1.0 =0.0 =0.4 (a) 0.0 0.2 0.4 0.6 0.8 1.0 140 150 160 170 180 190 200 210 220 Second mode c/b=.5, a/b=1.0 =0.0 =0.4 (b) Figure 3. (a) Frequency parameter λ vs. taper constant ; (b) Frequency parameter λ vs. taper constant . 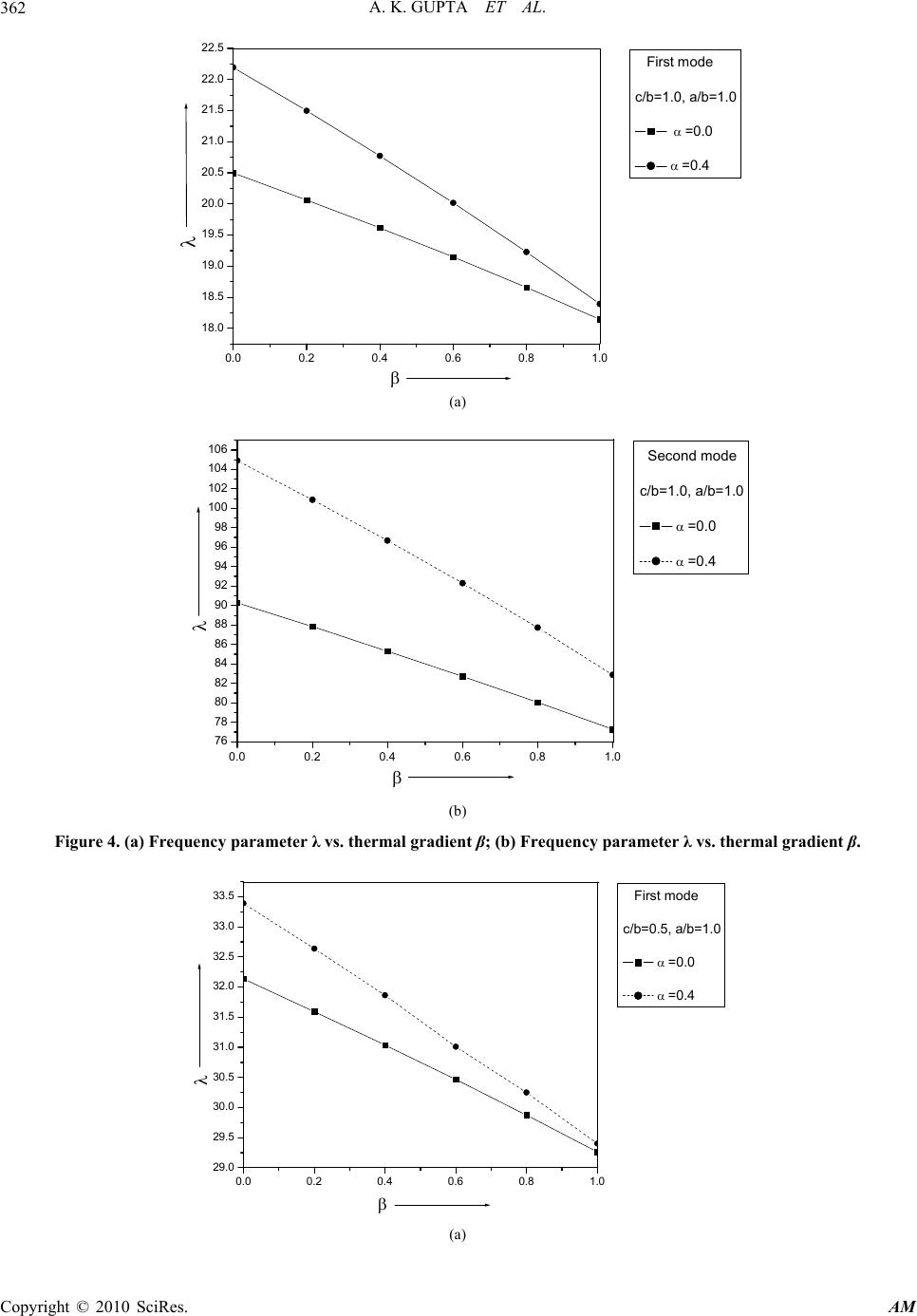 A. K. GUPTA ET AL. Copyright © 2010 SciRes. AM 362 0.0 0.2 0.4 0.6 0.8 1.0 18.0 18.5 19.0 19.5 20.0 20.5 21.0 21.5 22.0 22.5 First mode c/b=1.0, a/b=1.0 =0.0 =0.4 (a) 0.00.20.40.60.81.0 76 78 80 82 84 86 88 90 92 94 96 98 100 102 104 106 Second mode c/b=1.0, a/b=1.0 =0.0 =0.4 (b) Figure 4. (a) Frequency parameter λ vs. thermal gradient β; (b) Frequency parameter λ vs. thermal gradient β. 0.00.20.40.60.81.0 29.0 29.5 30.0 30.5 31.0 31.5 32.0 32.5 33.0 33.5 First mode c/b=0.5, a/b=1.0 =0.0 =0.4 (a)  A. K. GUPTA ET AL. Copyright © 2010 SciRes. AM 363 0.00.20.40.60.81.0 125 130 135 140 145 150 155 160 165 170 Second mode c/b=0.5, a/b=1.0 =0.0 =0.4 (b) Figure 5. (a) Frequency parameter λ vs. thermal gradient β; (b) Frequency parameter λ vs. thermal gradient β. 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 20 24 28 32 36 40 44 c/b First mode a/b=1.0 =0.0, =0.0 =0.0, =0.4 =0.4, =0.0 =0.4, =0.4 (a) 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 80 100 120 140 160 180 200 220 c/b Second mode a/b=1.0 =0.0, =0.0 =0.0, =0.4 =0.4, =0.0 =0.4, =0.4 (b) Figure 6. (a) Frequency parameter λ vs. c/b; (b) Frequency parameter λ vs. c/b.  A. K. GUPTA ET AL. Copyright © 2010 SciRes. AM 364 0.3 0.40.5 0.60.7 0.8 0.91.0 15 20 25 30 35 40 c/b First mode a/b=.75 =0.0, =0.0 =0.0, =0.4 =0.4, =0.0 =0.4, =0.4 (a) 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 60 70 80 90 100 110 120 130 140 150 160 c/b Second mode a/b=.75 =0.0, =0.0 =0.0, =0.4 =0.4, =0.0 =0.4, =0.4 (b) Figure 7. (a) Frequency parameter λ vs. c/b; (b) Frequency parameter λ vs. c/b. Figures 4 and 5 show that increase in thermal gradient the frequency decreases. The result is display- ed for the following two cases of taper constant: 0.0 , 0.4 . Also with increase in aspect ratio c/b the frequency de- creases for first two mode of vibration. Figures 6 and 7 show that with increase in aspect ratio c/b the frequency decreases for first two mode of vibra- tion. Also with increase in aspect ratio a/b the frequency increase for first two mode of vibration. Also the differ- ence be tween the lines of 0.0,0.0 and 0.4 , 0.4 is negligible. 5. Conclusions The Rayliegh-Ritz method has been successfully used to make a comprehensive study of the linear vibration characteristics of trapezoidal plates. Accurate data has obtained by varying the length ratios a/b and c/b. The results for trapezoidal plates of varying thickness are verified by the literature (4). It has been shown that the method provides accurate results. These results have been determined with considerable accuracy in order that they may serve as future data for researchers who desire to investigate the accuracy of their new numerical methods. 6. References [1] K. M. Liew and K. Y. Lam, “Vibrational Response of Symmetrically Laminated Trapezoidal Composite Plates with Point Constraints,” International Journal of Solids and Structures, Vol. 29, No. 24, 1992, pp. 1535-1547. [2] I. Chopra and S. Durvasula, “Vibration of Simply Sup- ported Trapezoidal Plates I. Symmetric Trapezoids,” Journal of Sound Vibration, Vol. 19, No. 4, 1971, pp. 379-392. [3] Y. Narita, K. Maruyama and M. Sonoda, “Transverse  A. K. GUPTA ET AL. Copyright © 2010 SciRes. AM 365 Vibration of Clamped Trapezoidal Plates Having Rec- tangular Orthotropy,” Journal of Sound Vibration, Vol. 77, 1981, pp. 345-356. [4] K. M. Liew and M. K. Lim, “Transverse Vibration of Trapezoidal Plates of Variable Thickness: Symmetric Trapezoids,” Journal of Sound Vibration, Vol. 165, No. 1, 1993, pp. 45-67. [5] M. S. Qatu, N. A. Jaber and A. W. Leissa, “Natural Fre- quencies for Completely Free Trapezoidal Plates,” Jour- nal of Sound Vibration, Vol. 167, No. 1, 1993, pp. 183- 191. [6] M. S. Qatu, “Vibrations of Laminated Composite Com- pletely Free Triangular and Trapezoidal Plates,” Interna- tional Journal of Mechanical Sciences, Vol. 36, No. 9, 1994, pp. 797-809. [7] D. V. Bambill, P. A. A. Laura and R. E. Rossi, “Trans- verse Vibrations of Rectangular, Trapezoidal and Trian- gular Orthotropic, Cantilever Plates,” Journal of Sound Vibration, Vol. 210, No. 2, 1998, pp. 286-290. [8] C. C. Chen, S. Kitipornchai, C. W. Lim and K. M. Liew, “Free Vibration of Cantilevered Symmetrically Lami- nated Thick Trapezoidal Plates,” International Journal of Mechanical Sciences, Vol. 41, No. 6, 1999, pp. 685-702. [9] H. T. Saliba, “Free Vibration Analysis of Simply Sup- ported Symmetrical Trapezoidal Plates,” Journal of Sound Vibration, Vol. 110, No. 1, 1986, pp. 87-97. [10] H. T. Saliba, “Transverse Free Vibration of Fully Clamped Symmetrical Trapezoidal Plates,” Journal of Sound Vibration, Vol. 126, No. 2, 1988, pp. 237-247. [11] A. Krishnan and J. V. Deshpande, “A Study on Free Vi- bration of Trapezoidal Plates,” Journal of Sound Vibra- tion, Vol. 146, No. 2, 1991, pp. 507-515. [12] A. K. Gupta and H. Kaur, “Study of the Effect of Ther- mal Gradient on Free Vibration of Clamped Visco-Elastic Rectangular Plates with Linearly Thickness Variation in both Directions,” Meccanica, Vol. 43, No. 3, 2008, pp. 449-458. [13] A. K. Gupta, T. Johri and R. P. Vats, “Study of Thermal Gradient Effect on Vibrations of a Non-Homogeneous Orthotropic Rectangular Plate Having Bi-Direction Line- arly Thickness Variations,” Meccanica, Vol. 45, No. 3, 2010, pp. 393-400. [14] A. K. Gupta, T. Johri and R. P. Vats, “Thermal Effect on Vibration of Non Homogeneous Orthotropic Rectangular Plate Having Bi-Directional Parabolic Ally Varying Thickness,” Proceedings of International Conference on Engineering & Computer Science, San Francisco, 2007, pp. 784-787. [15] A. K. Gupta and A. Khanna, “Vibration of Visco-Elastic Rectangular Plate with Linearly Thickness Variations in both Directions,” Journal of Sound Vibration, Vol. 301, No. 3-5, 2007, pp. 450-457. [16] C.-H. Huang, C.-H. Hsu and Y.-K. Lin, “Experimental and Numerical Investigations for the Free Vibration of Cantilever Trapezoidal Plates,” Journal of the Chinese Institute of Engineers, Vol. 29, No. 5, 2006, pp. 863-872. [17] J. S. Tomar and A. K. Gupta, “Effect of Thermal Gradi- ent on Frequencies of an Orthotropic Rectangular Plate Whose Thickness Varies in Two Directions,” Journal of Sound Vibration, Vol. 98, No. 2, 1985, pp. 257-262. [18] J. S. Tomar and A. K. Gupta, “Thermal Effect on Fre- quencies of an Orthotropic Rectangular Plate of Linearly Varying Thickness,” Journal of Sound Vibration, Vol. 90, No. 3, 1983, pp. 325-331. [19] N. J. Hoff, “High Temperature Effect in Air Craft Struc- tures,” Pergamon Press, New York, 1958. |

