V. M. R. M. PonRani et al. / Natural Science 2 (2010) 1318-1325
Copyright © 2010 SciRes. OPEN ACCESS
1323
(d)
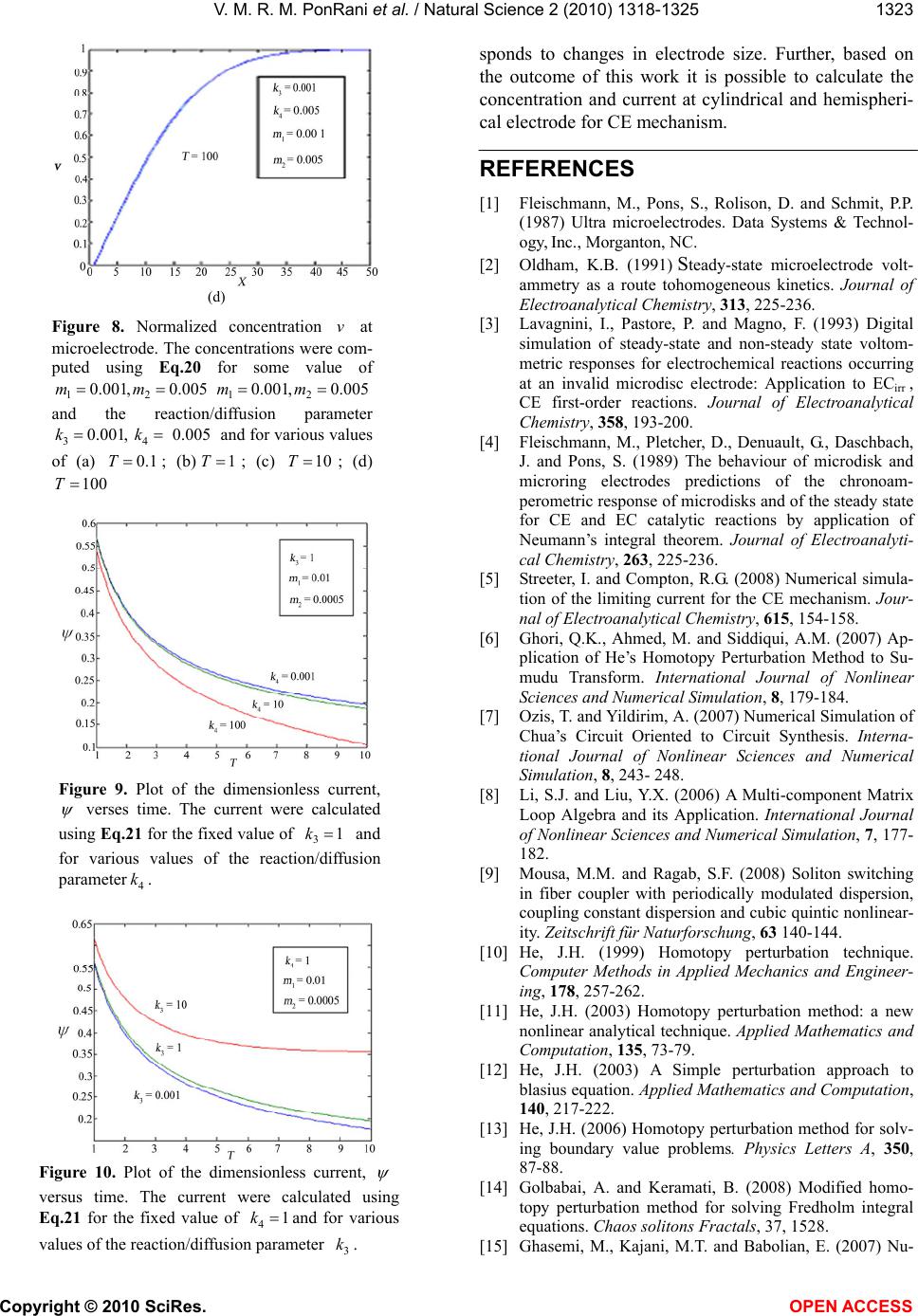
Figure 8. Normalized concentration v at
microelectrode. The concentrations were com-
puted using Eq.20 for some value of
12
0.001,0.005mm
12
0.001,0.005mm
and the reaction/diffusion parameter
34
0.001, 0.005 kkand for various values
of (a) 0.1
T; (b)1T; (c) 10T; (d)
100
T
Figure 9. Plot of the dimensionless current,
verses time. The current were calculated
using Eq.21 for the fixed value of 31k and
for various values of the reaction/diffusion
parameter 4
k.
Figure 10. Plot of the dimensionless current,
versus time. The current were calculated using
Eq.21 for the fixed value of 41kand for various
values of the reaction/diffusion parameter 3
k.
sponds to changes in electrode size. Further, based on
the outcome of this work it is possible to calculate the
concentration and current at cylindrical and hemispheri-
cal electrode for CE mechanism.
REFERENCES
[1] Fleischmann, M., Pons, S., Rolison, D. and Schmit, P.P.
(1987) Ultra microelectrodes. Data Systems & Technol-
ogy, Inc., Morganton, NC.
[2] Oldham, K.B. (1991) Steady-state microelectrode volt-
ammetry as a route tohomogeneous kinetics. Journal of
Electroanalytical Chemistry, 313, 225-236.
[3] Lavagnini, I., Pastore, P. and Magno, F. (1993) Digital
simulation of steady-state and non-steady state voltom-
metric responses for electrochemical reactions occurring
at an invalid microdisc electrode: Application to ECirr ,
CE first-order reactions. Journal of Electroanalytical
Chemistry, 358, 193-200.
[4] Fleischmann, M., Pletcher, D., Denuault, G., Daschbach,
J. and Pons, S. (1989) The behaviour of microdisk and
microring electrodes predictions of the chronoam-
perometric response of microdisks and of the steady state
for CE and EC catalytic reactions by application of
Neumann’s integral theorem. Journal of Electroanalyti-
cal Chemistry, 263, 225-236.
[5] Streeter, I. and Compton, R.G. (2008) Numerical simula-
tion of the limiting current for the CE mechanism. Jour-
nal of Electroanalytical Chemistry, 615, 154-158.
[6] Ghori, Q.K., Ahmed, M. and Siddiqui, A.M. (2007) Ap-
plication of He’s Homotopy Perturbation Method to Su-
mudu Transform. International Journal of Nonlinear
Sciences and Numerical Simulation, 8, 179-184.
[7] Ozis, T. and Yildirim, A. (2007) Numerical Simulation of
Chua’s Circuit Oriented to Circuit Synthesis. Interna-
tional Journal of Nonlinear Sciences and Numerical
Simulation, 8, 243- 248.
[8] Li, S.J. and Liu, Y.X. (2006) A Multi-component Matrix
Loop Algebra and its Application. International Journal
of Nonlinear Sciences and Numerical Simulation, 7, 177-
182.
[9] Mousa, M.M. and Ragab, S.F. (2008) Soliton switching
in fiber coupler with periodically modulated dispersion,
coupling constant dispersion and cubic quintic nonlinear-
ity. Zeitschrift für Naturforschung, 63 140-144.
[10] He, J.H. (1999) Homotopy perturbation technique.
Computer Methods in Applied Mechanics and Engineer-
ing, 178, 257-262.
[11] He, J.H. (2003) Homotopy perturbation method: a new
nonlinear analytical technique. Applied Mathematics and
Computation, 135, 73-79.
[12] He, J.H. (2003) A Simple perturbation approach to
blasius equation. Applied Mathematics and Computation,
140, 217-222.
[13] He, J.H. (2006) Homotopy perturbation method for solv-
ing boundary value problems. Physics Letters A, 350,
87-88.
[14] Golbabai, A. and Keramati, B. (2008) Modified homo-
topy perturbation method for solving Fredholm integral
equations. Chaos solitons Fractals, 37, 1528.
[15] Ghasemi, M., Kajani, M.T. and Babolian, E. (2007) Nu-