J. Mod. Phys., 2010, 1, 319-323
doi:10.4236/jmp.2010.15045 Published Online November 2010 (http://www.SciRP.org/journal/jmp)
Transition Metal-Nonmetal in Conductivity of Ceramic
Hole-Doped Cobaltites
Yurii Nikolaevich Chiang1, Mihail Olegovich Dzyuba1, Olga Georgievna Shevchenko1,
Anatolii Antonovich Kozlovskii2, Vitalii Philipovich Khirnyi2
1B.Verkin Institute for Low Temperature Physics and Engineering,
National Academy of Sciences of Ukraine, Kharkov, Ukraine
2Institute of Single Crystals, National Academy of Sciences of Ukraine,
Kharkov, Ukraine
Received September 17, 2010; revised November 8, 2010; accepted October 21, 2010
Abstract
In bulk granulated cobaltite La1–xSrxCoO3 with the size of granules of order of 1 micron at strontium hole
doping with replacement factor x = 0.35, a transition “metal-nonmetal” in the conductivity was revealed,
presumably connected with AFM ordering of the moments of granules. The assumption is proved by the
agreement between the experiment and results of calculation within the limits of a model offered for electron
transport based on the account of in-granule double exchange Zener mechanism and intergranule mechanism
of spin-polarized tunneling on the nearest neighbours with AFM exchange interaction. The calculation dif-
fers in that conductivities within granules are summarized, while total resistance of the system is represented
as a sum of resistances of the granules. In addition, the existence of AFM interaction between granules is
supported by the observed insensitivity of conductivity to a low external magnetic field (up to 5 kOe).
Keywords: Granulated Cobaltite, Double Exchange, Spin-Polarised Tunneling
1. Introduction
Intense interest is currently shown in researching trans-
port properties of the multicomponent compounds syn-
thesized on the basis of elements with prominent (pe-
rovskites) and even strong (oxipnictides with iron) mag-
netism. This results from the fact that the properties of the
above compounds are defined and are capable of being
controlled by a whole complex of the mechanisms of
interaction, including exchange mechanisms, which cor-
relate behavior of charge carriers. At that, the factor of
sample polycrystallinity which is characteristic, in par-
ticular, of the granulated composites of ceramic type,
brings its own share in even greater variety of properties.
Thus, during the study of magnetoresistance in ceramic
manganites, large magnetoresistance was found in low
fields below the ferromagnetic transition temperature TC
[l-4], while magnetoresistance of single crystals is either
quite small or completely absent under the same condi-
tions. At present, there exists an understanding that the
character of conductivity of granulated systems results
from two sources: in-granule (intrinsic) physical mecha-
nisms of conductivity and mechanisms of intergranule
interactions; this understanding exists in spite of the fact
that samples of granulated systems, even those synthe-
sized by the same solid-state technology, are capable of
being different in the character of the distribution of
granules, in their size, as well as in the percolation char-
acter of current flow.
Here, we study certain properties of granulated cobalt-
ites with La1–xSrxCoO3 (hereafter LSCO) composition, a
typical representative of the family of hole-doped com-
pounds based on transition metal oxides with perovskite
structure. In this family, the effects of correlation of
conduction electrons operated by doping can be treated
as intrinsic conductivity mechanisms. The level of dop-
ing sets the size and sign of exchange interactions as
parameters of correlation between local ionic magnetic
moments and spins of delocalized conduction electrons
[1-3]. These quantities define the type of interaction,
including ferromagnetic, when electrons are transmitted
in accordance with the scheme of double exchange [4].
Other intrinsic mechanisms of conductivity may include
in-granule electron transport mechanisms of the Mott
type arising under the conditions of aperiodical field of
force in a general sense [5].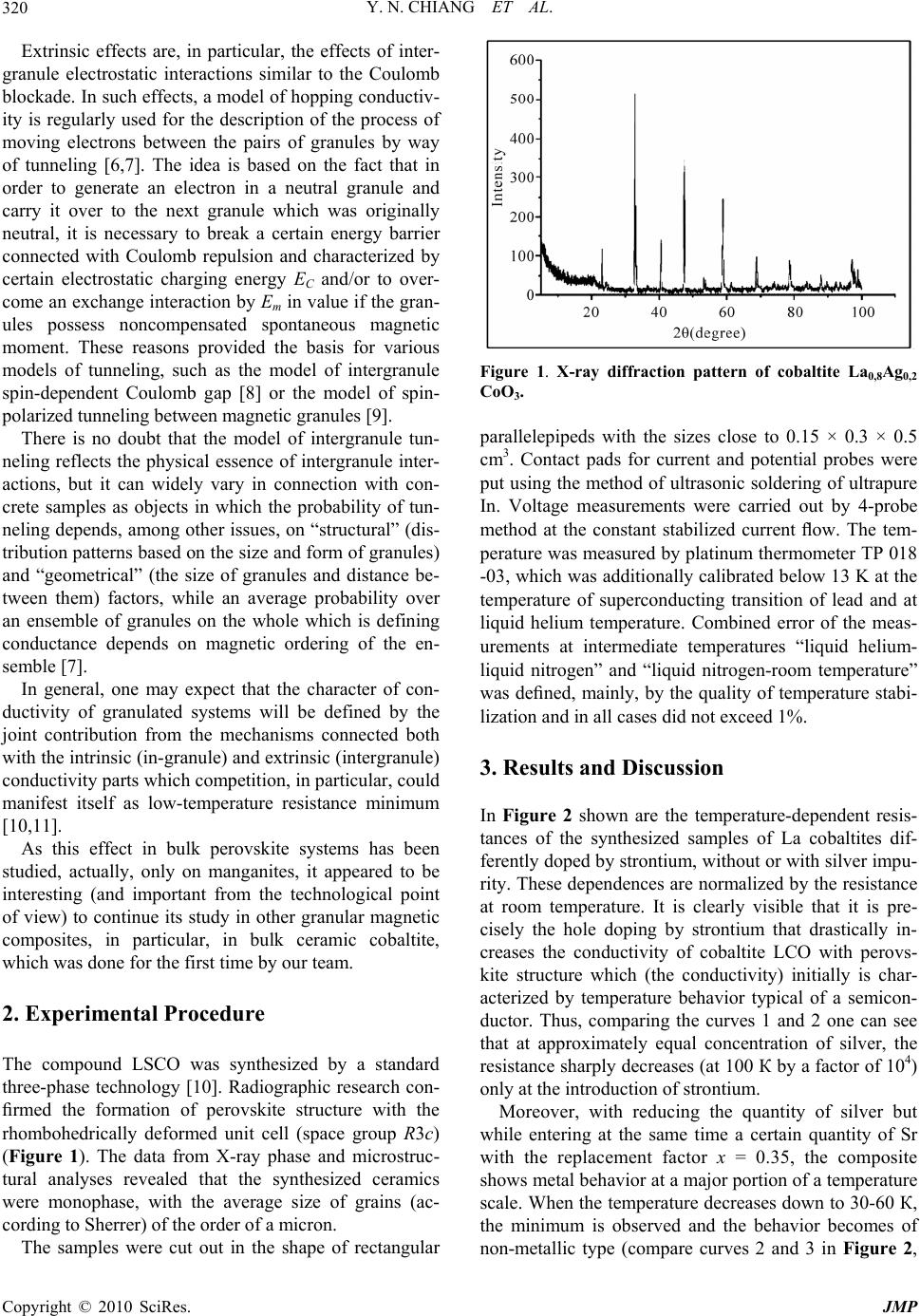

Y. N. CHIANG ET AL. 320
Extrinsic effects are, in particular, the effects of inter-
granule electrostatic interactions similar to the Coulomb
blockade. In such effects, a model of hopping conductiv-
ity is regularly used for the description of the process of
moving electrons between the pairs of granules by way
of tunneling [6,7]. The idea is based on the fact that in
order to generate an electron in a neutral granule and
carry it over to the next granule which was originally
neutral, it is necessary to break a certain energy barrier
connected with Coulomb repulsion and characterized by
certain electrostatic charging energy EC and/or to over-
come an exchange interaction by Em in value if the gran-
ules possess noncompensated spontaneous magnetic
moment. These reasons provided the basis for various
models of tunneling, such as the model of intergranule
spin-dependent Coulomb gap [8] or the model of spin-
polarized tunneling between magnetic granules [9].
There is no doubt that the model of intergranule tun-
neling reflects the physical essence of intergranule inter-
actions, but it can widely vary in connection with con-
crete samples as objects in which the probability of tun-
neling depends, among other issues, on “structural” (dis-
tribution patterns based on the size and form of granules)
and “geometrical” (the size of granules and distance be-
tween them) factors, while an average probability over
an ensemble of granules on the whole which is defining
conductance depends on magnetic ordering of the en-
semble [7].
In general, one may expect that the character of con-
ductivity of granulated systems will be defined by the
joint contribution from the mechanisms connected both
with the intrinsic (in-granule) and extrinsic (intergranule)
conductivity parts which competition, in particular, could
manifest itself as low-temperature resistance minimum
[10,11].
As this effect in bulk perovskite systems has been
studied, actually, only on manganites, it appeared to be
interesting (and important from the technological point
of view) to continue its study in other granular magnetic
composites, in particular, in bulk ceramic cobaltite,
which was done for the first time by our team.
2. Experimental Procedure
The compound LSCO was synthesized by a standard
three-phase technology [10]. Radiographic research con-
firmed the formation of perovskite structure with the
rhombohedrically deformed unit cell (space group R3c)
(Figure 1). The data from X-ray phase and microstruc-
tural analyses revealed that the synthesized ceramics
were monophase, with the average size of grains (ac-
cording to Sherrer) of the order of a micron.
The samples were cut out in the shape of rectangular
Figure 1. X-ray diffraction pattern of cobaltite La0,8Ag0,2
CoO3.
parallelepipeds with the sizes close to 0.15 × 0.3 × 0.5
cm3. Contact pads for current and potential probes were
put using the method of ultrasonic soldering of ultrapure
In. Voltage measurements were carried out by 4-probe
method at the constant stabilized current flow. The tem-
perature was measured by platinum thermometer TP 018
-03, which was additionally calibrated below 13 K at the
temperature of superconducting transition of lead and at
liquid helium temperature. Combined error of the meas-
urements at intermediate temperatures “liquid helium-
liquid nitrogen” and “liquid nitrogen-room temperature”
was defined, mainly, by the quality of temperature stabi-
lization and in all cases did not exceed 1%.
3. Results and Discussion
In Figure 2 shown are the temperature-dependent resis-
tances of the synthesized samples of La cobaltites dif-
ferently doped by strontium, without or with silver impu-
rity. These dependences are normalized by the resistance
at room temperature. It is clearly visible that it is pre-
cisely the hole doping by strontium that drastically in-
creases the conductivity of cobaltite LCO with perovs-
kite structure which (the conductivity) initially is char-
acterized by temperature behavior typical of a semicon-
ductor. Thus, comparing the curves 1 and 2 one can see
that at approximately equal concentration of silver, the
resistance sharply decreases (at 100 К by a factor of 104)
only at the introduction of strontium.
Moreover, with reducing the quantity of silver but
while entering at the same time a certain quantity of Sr
with the replacement factor x = 0.35, the composite
shows metal behavior at a major portion of a temperature
scale. When the temperature decreases down to 30-60 К,
the minimum is observed and the behavior becomes of
non-metallic type (compare curves 2 and 3 in Figure 2,

Y. N. CHIANG ET AL. 321
as well as the curve 1, Figure 2, for LACO without Sr
and the curve for LSCO without Ag in Figure 3). Ap-
parently, we have received an additional confirmation of
the insignificant role of silver for the correlation of elec-
trons in cobaltites by means of exchange processes with
the participation of oxygen ions, probably, because of
weak reactivity and oxidizing power of this element or at
least in the composites of the chemical compound that
we studied. Notice that the transition of such a type is
observed in bulk samples of granulated cobaltite LSCO,
with the size of grain 1 micron and the specified degree
of doping by strontium, for the first time. Such transition,
for example, was not observed in bulk ceramics of the
Figure 2. Resistance of hole-doped cobaltite LSACO nor-
malized by the resistance at 300 K in dependence of tem-
perature, at various doping levels. R300K, Ohm—1: 2.42; 2:
0.0077; 3: 0.0026.
Figure 3. Minimum on the temperature dependence of the
normalized resistance of hole-doped cobaltite LCO at the level
of replacement of lanthanum by strontium x  0.35. R300K: for
LSCO—4.7 × 10–4 Ohm; for LSACO see Caption to Figure 2.
Points: experiment; solid lines: fit in accordance with (1), see
text. Inset: R(T) LSACO at H = 0 (circles) and 5kOe (line).
same cobaltite but with the size of grain  50 micron and
with x > 0.35 [13]. It indicates that the effect is not only
rather critical to the level of hole doping, which in gen-
eral is characteristic of conductivity of perovskite com-
pounds based on oxides of transition metals, but also to
structural characteristics such as the size and density of
distribution of grains.
Part of the resistance curves (normalized for the resis-
tance at 300 K) with a minimum corresponding to the
transition from metal to non-metal behavior of conduc-
tivity is presented in Figure 3. The presence of the min-
imum, as well as of any extremum, on the R(T) depend-
ences means the existence in corresponding temperature
regions of competing scattering mechanisms or of elec-
tron correlation with contributions into conductivity com-
parable in value. This allows us to apply for the explana-
tion of this phenomenon those theoretical concepts the
use of which for the description of experimental data
would lead to reasonable values of theoretical parameters,
thereby confirming the rationality of the theoretical mod-
els themselves. Choosing the concept of two contribu-
tions, intrinsic and intergranule, we, thereby, accept that
the resistance of the system is an additive sum of in-
granule resistances (Rg) and intergranule “resistances”
(resistive contributions from intergranule interactions,
Rispt). Then, it is possible to represent the total resistance
of the system normalized, for example, by that resistance
at 300 K, in the following way:

11
300K
(300K) ρ;
gispt
T
RT RGG



 (1)
;
;σ
g
ispt
gispt
G,
where brackets mean the averaging of corresponding
contributions to the conductivity  over the ensemble of
granules, G is the conductance averaged over the sample,
300K the resistivity at 300 K.
As is known, the systems of (Re) SCO type (Re is a
trivalent rare-earth element) are double-phase systems
[3]. One of the phases, matrix ReCO, can be character-
ized by a thermally activated mechanism of conductivity
of semiconductor type, sm (for example, of the Mott
type [5]) while the conductivity of the other phase is that
of SCO sublattice, DE, due to the mechanism of double
ferromagnetic exchange between cobalt ions of different
valence by means of the conduction electrons [4]. As a
result, the intrinsic contribution of a granule into conduc-
tivity can be written as g = sm + DE, where the granule
conductance will make [14]:






2
σσ σexp α
m
sm DEC
GgTe ah TT

 
(2)
Here,  = (T );

the band gap; α = |Co 4+| /
|Co 3+| is a portion of Co4+ ions, TC the Curie temperature,

Y. N. CHIANG ET AL. 322
Figure 4. Normalized resistivity curve with a minimum
(points) and the fit calculated from (1) (solid line 1). Shown
separately are the intrinsic contribution from the granules
(curve 3, SM+DE) and the int ergranule contribution (curve
2, ISPT). Curve 4: spin correlation function for AFM in-
teraction betwee n gr anules.
a the lattice parameter, h the Planck constant, and m can
accept values 1 (the Arrenius law), 1/2 (when the Cou-
lomb gap is present [7]), or 1/4 (in case of variable range
hopping conductance [5]). As it was discovered in [14],
at low temperatures in cobaltites the mechanism of dou-
ble ferromagnetic exchange prevails, causing metal be-
havior of conductivity at suffcient level of hole doping
characterized by the α parameter.
An alternative contribution to the conductivity of the
granulated magnetic system can be made by an extrinsic
intergranule mechanism of conductivity which is based
on the principle of spin-polarized tunneling [6,7]. The
given model assumes that when an electron is tunnelling
through a boundary between two granules with the anti-
parallel magnetization, it will meet a potential barrier of
order of the exchange energy J in size which fact reduces
the probability of tunneling, i. e . , the conductivity, by the
factor of e –J/kT in comparison with the case of ferromag-
netic orientation of vectors of the magnetization of gran-
ules. As it was later shown in [9], the model predicts
sharp increase in the considered contribution to conduc-
tivity even in low magnetic fields  1 kOe, in case the
initial (in the zero field) distribution of directions of the
magnetizations of granules was random (paramagnetic).
The effect should have obviously been absent if the dis-
tribution in the zero field was close to antiferromagnetic
(АFМ). It follows from the data in Figure 3 that the
influence of the magnetic field up to 5 kOe on conductiv-
ity of the samples with x = 0.35 is practically absent.
This fact allows us to assume AFM orientation of the
magnetizations of granules in the zero field in these sam-
ples. Indications of АFМ exchange between the granules
are also available in [9,15,16].
In [9], the expression for intergranule conductivity for
two granules conditional upon the tunneling of spin -
polarized electrons was derived as




22
σ121 cosθ
ispt nn P

 , (3)
where polarization P = (n – n) / (n + n); n, is the
density of states of the electrons at Fermi – level with
spin upwards and downwards, accordingly. The expres-
sion establishes the dependence of intergranule conduc-
tivity on the  angle between the directions of magneti-
zation of the neighboring granules. Averaging (3) over
cos  and over probabilities of tunneling between pairs
of two nearest neighbors (so-called n-n model) for the
whole ensemble of the system granules, as well as ac-
counting for the temperature dependence of probability
of tunneling of thermoactivated charge carriers and АFМ
interaction of granules [6,7,11,16-18] allows us to pre-
sent intergranule conductance as follows
 

12
σ(0) ρ1cosθ
ispt
isptCn n
GTTUP




(4)
where U is the height of intergranule potential barrier;
n–n(U) = 0 + T3/2 [17,18]; < cos  > = [coth(J/T) –
(J/T)–1] the spin correlation function < S1 · S2 > [11,19].
Combining (2) and (4), in accordance with (1), we can
get the total (normalized) resistance of the sample. As-
suming that the temperature behavior of intrinsic con-
ductivity of granules in cobaltites can be of rather gen-
eral character, in (2) we have kept the values of a band
gap  = 100 K in 
sm and of the temperature of AFM
ordering TC = 160 K the same, as been received at the
description of low-temperature part of R(T) for Er co-
baltites in [14]. Besides, assuming the similarity of mag-
netic properties of cobaltites with close stoichiometry,
we used a uniform value of exchange energy J for the
analyzed samples. It has actually narrowed the number of
varied fitting parameters to two, namely, 0 and . This
can easily be seen from the Table 1 where the main pa-
rameters obtained for the curves fitted to the experimen-
tal data are presented. The concurrence between calcu-
lated and experimental data in the region of resistance
minimum for the analyzed samples gives ground for the
conclusion that the intrinsic conductivity of granules in
different samples of compositions with close stoichiome-
try is defined by practically universal mechanisms of
transport (as the values of α and  can be set invariable),
while the position and the depth of the minimum, all
other conditions being equal, depend mainly on the
probability of intergranule spin-polarized tunneling
characterized by the intergranule resistance n–n(U), i.e.,
on the values of 0 and . Though we used n–n(U) in the
form suggested in [17,18], however, the experimental

Y. N. CHIANG ET AL. 323
Table 1. The main parameters obtained for the curves fitted to the experimental data.

300K Ohm cm

0Ohm cm α


3/2
Ohm cm K  2 P


KJ
LaSrAgCoO 3 1.95 10

 4 1.68 10

 1

0.05 0.37 100
LaSrCoO 3 3.9 10

 4 0.8 10

 1

0.08 0.35 100
curve actually reveals stronger dependence of n–n(U) on
temperature than when considering only a spin-wave
term  T3/2. Probably it is necessary to also consider the
temperature dependence of the unbalance in the density
of states for carriers with alternate spins.
4. Conclusions
In conclusion, the conductivity of bulk granulated co-
baltites La1–xSrxCoO3 was studied with the size of gran-
ules of order of 1 micron and the replacement rate of
lanthanum by strontium x  0.35. The transition «metal –
nonmetal» in conductivity is observed at temperatures
below the temperature of magnetic transition, presuma-
bly connected with АFМ ordering of the magnetization
of granules. The analysis of the observed phenomenon is
carried out based on allowing for in-granule mechanism
of the Zener double exchange and intergranule mecha-
nism of spin-polarized tunneling between the nearest
neighbors with АFМ exchange interaction. The existence
of AFМ interaction of granules is additionally confirmed
by the fact that the value of conductivity is insensitive to
low external magnetic field (up to 5 kOe). Microscopic
parameters of double exchange and spin-polarized tun-
neling are estimated.
5. References
[1] A. Georges, G. Kotliar, W. Krauth, and M. J. Rozenberg,
Reviews of Modern Physics, Vol. 68, 1996, p. 13.
[2] V. M. Loktev and Yu. G. Pogorelov, Low Temperature
Physics, Vol. 26, 2000, p. 171.
[3] Yu. A. Izyumov, Yu. N. Skryabin, Physics-Uspekhi, Vol.
44, 2001, p. 109.
[4] C. Zener, Physical Review, Vol. 82, 1951, p. 403.
[5] N. F. Mott, E. A. Davis, “Electron Processes in Non-
Crystalline Materials”, Clarendon Press, Oxford, 1979.
[6] P. Sheng, B. Abeles and Y. Arie, Physical Review Letters,
Vol. 31, 1973, p. 44.
[7] J. S. Helman and B. Abeles, Physical Review Letters, Vol.
37, 1976, p. 1429.
[8] J. M. D. Coey, A. E. Berkowitz, L. Balcells, F. F. Putris,
and A. Barry, Physical Review Letters, Vol. 80, 1998, p.
3815.
[9] P. Raychaudhuri, K. Sheshadri, P. Taneja, S. Bandyop-
adhyay, S. Chaudhary and S. B. Roy, Physical Review,
Vol. 59, 1999, p. 3919.
[10] M. Garsia-Hernandez, F. Guinea, A. de Andres, J. L.
Martinez, C. Prieto and L. Vazquez, Physical Review,
Vol. 61, 2000, p. 9549.
[11] M. I. Auslender, E. Rozenberg, A. E. Kar’kin, B. K.
Chaudhuri and G. Gorodetsky, Journal of Alloys and
Compounds, Vol. 326, 2001, p. 81.
[12] A. G. Gamzatov, A. B. Batdalov, O. V. Melnikov, O. Yu.
Gorbenko, Izvestiya RAN, Seriya Fizicheskaya, Vol. 73,
2009, p. 1377.
[13] B. I. Belevtsev, N. T. Cherpak, I. N. Chukanova, A. I.
Gubin, V. B. Krasovitsky and A. A. Lavrinovich, Journal
of Physics: Condensed Matter, Vol. 14, 2002, p. 2591.
[14] Yu. N. Chiang, V. Ph. Khirnyi, O. G. Shevchenko and A.
A. Kozlovskii, Low Temperature Physics, Vol. 35, 2009,
p. 876.
[15] A. E. Kar’kin, D. A. Shulyatev, A. A. Arsenov, et al.,
Zhurnal Eksperimentalnoii i Teoreticheskoii Fiziki, Vol.
89, 1999, p. 9358.
[16] E. Rozenberg, M. I. Auslender, I. Felner and G.
Gorodetsky, Journal of Applied Physics, Vol. 88, 2000, p.
2578.
[17] N. Zhang, F. Wang, W. Zhong and W. Ding, Solid State
Communications, Vol. 107, 1998, p. 417.
[18] N. Zhang, W. Ding, W. Zhong, D. Xing and Y. Du, Phy-
sical Review, Vol. B 56, 1997, p. 8138.
[19] O. Ciftija, M. Luban, M. Auslender and J. H. Luscombe,
Physical Review, Vol. B 60, 1999, p. 10122.