J. Mod. Phys., 2010, 1, 312-318
doi:10.4236/jmp.2010.15044 Published Online November 2010 (http://www.SciRP.org/journal/jmp)
Formation of Neutron-Rich and Superheavy
Elements in Astrophysical Objects
Rabinarayan Panda1, Suresh Kumar Patra2
1Department of Physics, ITER, Siksha O Anusandhan University, Bhubaneswar, India
2Institute of Physics, Sachivalaya Marg, Bhubaneswar, India
Received August 9, 2010; revised September 13, 2010; accepted September 9, 2010
Abstract
We calculate the reaction and the fusion cross-sections of neutron-rich heavy nuclei taking light exotic iso-
topes as projectiles. Results of neutron-rich Pb and U isotopes are demonstrated as the representative targets
and He, B as the projectiles. The Gluaber Model and the Coupled Channel Formalism are used to evaluate
the reaction and the fusion cross-sections for the cases considered. Based on the analysis of these cross-sec-
tions, we predict the formation of heavy, superheavy and super-superheavy elements through rapid neutron/
light nuclei capture r-process of the nucleosynthesis in astrophysical objects.
Keywords: Total Nuclear Cross Section, Fusion Reaction Cross Section, Gluaber Model, Coupled Channel
Formalism
1. Introduction
Formation of superheavy elements (SHE) in the laboratory
is one of the most challenging problems in Nuclear Phys-
ics. So far the synthesis of Z = 118 element has been pos-
sible [1]. Efforts are on to synthesize still heavier elements
in various laboratories all over the world. It is certain that
if an element is created through human efforts then most
probably it may be present naturally somewhere in the
Universe. Thus the mode of formation of superheavy or
super-superheavy element in astrophysical object is a fun-
damental question in the field of Nuclear Astrophysics. In
this context, it is likely that the superheavy element with Z
= 118 and higher atomic numbers are present. It has been
reported in Ref. [2], and the stability of the most stable
superheavy elements could be as high as 109 years in some
of the calculations [3-7]. Thus, the study of unstable nuclei
with radioactive ion beam (RIB) facilities has opened an
exciting channel to look up to some of the crucial issues in
the context of both nuclear structure and astrophysics [8].
Unstable nuclei play an influential, and in some cases
dominant role.
The direct study of stellar properties in ground-based
laboratories has become feasible, due to the availability
of RIBs; for example the study of 18Ne induced neutron
pick-up reaction could reveal inform-tion about the ex-
otic 15O+19Ne reaction occurring in the CNO cycle in
stars. Study of the structure and the reactions of not only
unstable light exotic but also of the superheavy and the
super-superheavy nuclei is therefore required to improve
our understanding of the astrophysical origin of atomic
nuclei and the evolution of stars and their death, because,
the formation of neutron-rich/super-superheavy nuclei
determine the endpoint of the rapid-neutron (rn-) capture
process in nucleosynthesis.
In a recent study, Satpathy et al. [9] claimed the neu-
tron-rich U and Th-isotopes are thermally fissile and
could release orders of magnitude more energy than 235U
in a new mode of fission decay called multi-fragmenta-
tion fission, which happened frequently in astrophysical
objects, which may cause the termination of the rn-cap-
ture process. The main objective of the present letter is to
study the reaction (σr) and fusion (σf) cross-sections of
neutron-rich U and some other interesting exotic isotopes,
which are related to the formation of neutron-rich, SHE
and super-SHE elements in the Universe. The value of σr
is calculated by using the most recently developed effec-
tive field theory motivated relativistic mean field (E-
RMF) nuclear densities [10-13], in conjunction with the
Glauber model. However, σf is estimated in the non-
relativistic coupled channel calculation. From the calcu-
lated reaction and fusion cross-sections, we look for the
formation path of neutron rich, SHE and super-SHE nu-
clei in the cosmos.

R. PANDA ET AL. 313
2. Theoretical Formalism
The theoretical formalism to calculate the nuclear reac-
tion cross-section using Glauber approach has been given
by R. J. Glauber [14]. The standard Glauber form for the
reaction cross-section at high energies is expressed [14]
as:

0
21
rbTbdb


 

, (1)
where T(b), the transparency function, is the probability
that at an impact parameter b the projectile passes
through the target without interaction. This function T(b)
is calculated in the overlap region between the projectile
and target where the interactions are assumed to result
from single nucleon-nucleon collision and is given by


,
() expijti pj
ij
Tbdssb ss 

 




(2)
Here, the summation indices i, j run over proton and
neutron numbers and subscript p and t refer to projectile
and target respectively.
The original Glauber model is designed for high en-
ergy projectile, like relativistic proton reactions. It fails
to describe the collisions induced at relatively low ener-
gies. In this case, the straight-line trajectory is modified
because of the presence of the Coulomb field of the tar-
get and projectile. In such cases the present version of
Glauber model is modified in order to take care of finite
range effects [15] in the profile function and the Cou-
lomb modified trajectories. Thus for finite range ap-
proximations, the transparency function is given by

,
() expij
ij
PT
Tbb s t



 




 




Pi Tj
tsdsdt 
 


, (3)
Here the profile function ij
 is given by

2
22
1exp ,
22
eff
ij effij
NN NN
b
i
b

 


 



where tsbbeff



 , b

is the impact parameter, s

and t

are just the dummy variables for integration over
the z-integrated target and projectile densities. The val-
ues of the parameters, ij

,

and NN

are taken
from Ref. [16-18]. The detailed formalism is available in
Ref. [19-21]. The E-RMF density with G2 parameter set
[10-13,22,23] is used as input for the evaluation of σr.
For the details of the calculation of ground state proper-
ties of finite nuclei and the procedure of estimation of
nuclear reaction cross-section, we refer the reader to Refs.
[19-24]. To compute the fusion cross-section σf we fol-
low the coupled-channel calculations including all orders
of coupling. This is done in a non-relativistic framework.
The computer code CCFULL as developed in Ref. [25]
is used. The fusion cross-section is given by the formula
[25]:
  
2
0
21
fJ J
JJ
EE JPE
k



 , (4)
with PJ(E) is the inclusive penetrability and the other
symbols have the standard meaning as defined in [25].
3. Calculations and Results
It was shown in our earlier papers that the densities taken
from relativistic mean field formalism, and used in the
frame-work of Glauber model [14,24] to evaluate the
differential and total reaction cross-section is quite suc-
cessful for light systems [19-21]. Now we extend the
model to calculate the total reaction cross-section con-
sidering light exotic nuclei as projectile and heavy neu-
tron-rich isotopes as target. Here, we calculate as the
representative cases for the reaction cross-section of
neutron-rich Pb and U isotopes taking exotic He and B
nuclei as incident projectile. In Figure 1 the reaction
cross-section σr for 4He + 208,228,248,278Pb, 10,15,17,20B +
208Pb, 4He + 235,250,270,290U and 10,15,17,20B + 235U are pre-
sented. From the calculated results, the increase in σr is
quite substantial with the target mass. The same observa-
tion is also applicable, while increasing the mass of the
projectile (keeping the target mass constant). In any of
these cases, the reaction cross-section becomes favorable
with either increase of projectile mass or the mass of the
target or both. The enhancement can be understood by
the simple geometrical area of the nucleus πR2, where R
is the sum of the radii of the target and the projectile. The
nuclear radius with the mass number is connected with
the relation R = r0A1/3, where r0 = 1.36 fm and one expect


2
3/13/1
ptr AA 
 . Bradt and Peters [26] modified this
relation to take into account the deviation from the ex-
perimental systematic and it is expressed as

2
21/31/3
00rtp
rA Ab 




, where 0
b = 2.247 – 0.915


3/13/1 tp AA . This formula is further improved in
[27,28] and later on the Coulomb correction was included
[29,30]. The semi-empirical formula to calculate the total
nuclear reaction cross-section [31,32] and experimental
measurements [33,34] also shows the size dependence of
σr on the masses of target and projectile [33,34]. This
implies the probability of formation of heavier masses in
the reaction process with heavier isotope of the projectile
as well as target. In Ref. [35], within the formalism of a
Thomas-Fermi model, calculations are presented for nu-

R. PANDA ET AL. 314
clei beyond the nuclear drip-line at zero temperature. This
is possible because of the presence of an external neutron
gas which may be envisaged in the astrophysical scenario
and is the situation of the present discussion for accreting
cosmological objects.
In Figure 2 the fusion cross section σf for various neu-
tron-rich light nuclei with heavier drip-line isotopes like
4He+208,228, 2 48 ,2 78Pb, 10,15,17,20B+208Pb, 4He+235,250,270,290U
Figure 1. Th e nucl ear rea ction c ross-sect ions tak ing He and B is otopes as projecti le with differen t isotop es of Pb and U.
Figure 2. The nuclear fusion cross-sect i on s taking He and B isotopes as projectile with different isotopes of Pb and U.

R. PANDA ET AL. 315
and 10,15,17,20B+235U are shown. Similar to the reaction
cross-section, the increase in σf is quite clear with the
increase of target, projectile or both the masses. This
implies the probability of creation of heavier masses with
the increase of mass number of the projectile as well as
target and making the way for the evolution of neutron-
rich heavy nuclei much beyond the drip-line [35] due to
the presence of the external neutron gas or highly neu-
tron-rich light as well as heavy nuclei generates in the
astrophysical objects.
Analysis of Figures 1 and 2 shows that, the magnitude
of σr and σf is optimum at ~ 30 to 200 MeV of the inci-
dent projectile energy. Beyond this range, the value of σr
and σf decreases drastically. Both the cross-sections in-
dicate the suitability of the incident projectile energy for
a favorable condition of the formation of the fused ele-
ments in the astrophysical system. Thus, the chance of
the formation of heavier element is maximum, if a suit-
able energy range is created. A possible system for such
case may be relativistic jets of Gamma Ray Burst (GRBs)
or supernovae jets near the nascent neutron star [36,37].
The high energy environment in such cosmological ob-
jects is because of the supernova shock [38] and it is
quite common in the nascent neutron star or relativistic
jets of GRBs [36,37].
In these objects a highly neutron-rich and high tem-
perature scenario is made possible and which may be a
probable platform for such reactions. In this context, it is
worth citing the following example: A neutron star is
burned when a star of mass ~ 20 M⊙ undergoes its core
collapses after hyper-energetic explosions of Gamma ray
bursts. A star with initially ~ 20 M⊙ would develop car-
bon-oxygen core of ~ 3.3 M⊙. It left behind a neutron star
of ~ 1.4 M⊙, ~ 1.3 M⊙ of oxygen and ~ 0.6 M⊙ of
heavier elements, Si and Fe group, which could be ejected
in the supernova. Such a collapse gives rise to an explo-
sion of kinetic energy K. E. ~ 1051 ergs (~ 6.25 × 1056 MeV)
[36,37]. Young neutron stars have a fluid surface, a solid,
crystalline crust and a fluid interior. The fluid regions of
the star adjust themselves to its rotation which remaining
always asymmetric. The radiated power comes directly
from the rotational energy of the neutron star. The entropy
in mass elements exhibiting the neutron star at later times
will be larger than the earlier. This is because, most of the
heating occurs near the surface of the neutron star. Slowly
with time the radius of the neutron star shrinks from 100
Km to 10 Km [39,40]. The decrease in the initial radius
start from which the mass elements begin increasing the
heat rate [36,37]. It is worth mentioning of the burning
process of H, He, Li ... in the accreting astrophysical
system. To maintain hydrostatic equilibrium [41], this
continues up to formation of Iron. When this stage is
reached, depending on its mass, the astrophysical object
undergoes various phenomena like supernovae explosion,
X-rays burst, GRBs, formation of neutron star, black hole,
red giant or white dwarf etc. In some cases, it becomes
highly neutron-rich/light-nuclei (He, Li, Be...) environ-
ment which is favorable for the fusion of such low mass
nuclei and could makes the way for the formation of
heavier isotopes. This process supposes to continue up to
certain A or Z number. Slowly, this fusion process be-
comes less favorable, as they can not overcome the Cou-
lomb barrier. After this stage, the rn-capture process gains
importance which prolongs for a longer time for the for-
mation of ultra-heavy nuclei.
Thus, in the course of time, the neutron-rich light ele-
ment fused with these heavy nuclei and more heavier
isotopes with a little increase of proton number is gener-
ated in the process; for example, 4He+208Pb gives 212Po.
Again 212Po reacts with 4He to form 216Rn. A schematic
diagram for the process of SHE formation is shown in
Figure 3.
From the figure, it can be understood how this phe-
nomenon goes on to create much heavier isotopes. Simi-
larly other processes also continue to go on as shown in
Figures 1, 2 and 3, such as 20B+235U→255Bk,20B+255Bk
→275No..... and so on. A representative example is de-
picted in Figure 4. As mentioned earlier, after the su-
pernovae explosion, in the rn-process, heavy normal/
exotic nuclei including the ultra-neutron rich light iso-
topes are formed. Exotic nuclei like 6He, 11Li, 14Be, 20B,
normal actinides (e.g. 208Pb, 235U etc.) and neutron-rich
drip-line isotopes, similar to 278Pb etc. are generated.
Thereafter, fusion process of the light isotopes with
heavier nuclei becomes important. The increase of fusion
cross-sections as shown in Figure 4 confirmed the pos-
sibility of the formation of ultra-heavy isotopes as well as
super heavy elements both with lower and higher atomic
masses. The demonstration of a path for the formation of
408X132 (A = 408, Z = 132, N = 276) through complete
fusion process is given below (whose cross-sections are
shown in Figure 4):
20B+208Pb→228Fr, 20B+228Fr→ 248U, 20B+248U→ 268Bk,
20B+268Bk→ 288No, 20B+288No→ 308Bh, 20B+308Bh→
328X112, 20B+328X112 → 348X117, 20B+348X117 → 368X122,
20B+368X122 → 388X127, 20B+388X127 → 408X132 and so on.
Thus, each time the proton number Z increases by 5 units
the mass number A goes up by 20 units in the case of 20B
capture. Slowly, it creates a highly neutron-rich heavy
isotope, which is enabled to capture any more neutron n or
neutron-rich nucleus. This is termed as waiting point.
Here, the neutron-rich heavy element emits a β−
particle,
and the daughter nucleus gains a positive charge by con-
verting a neutron (n) to a proton (p). Due to this en-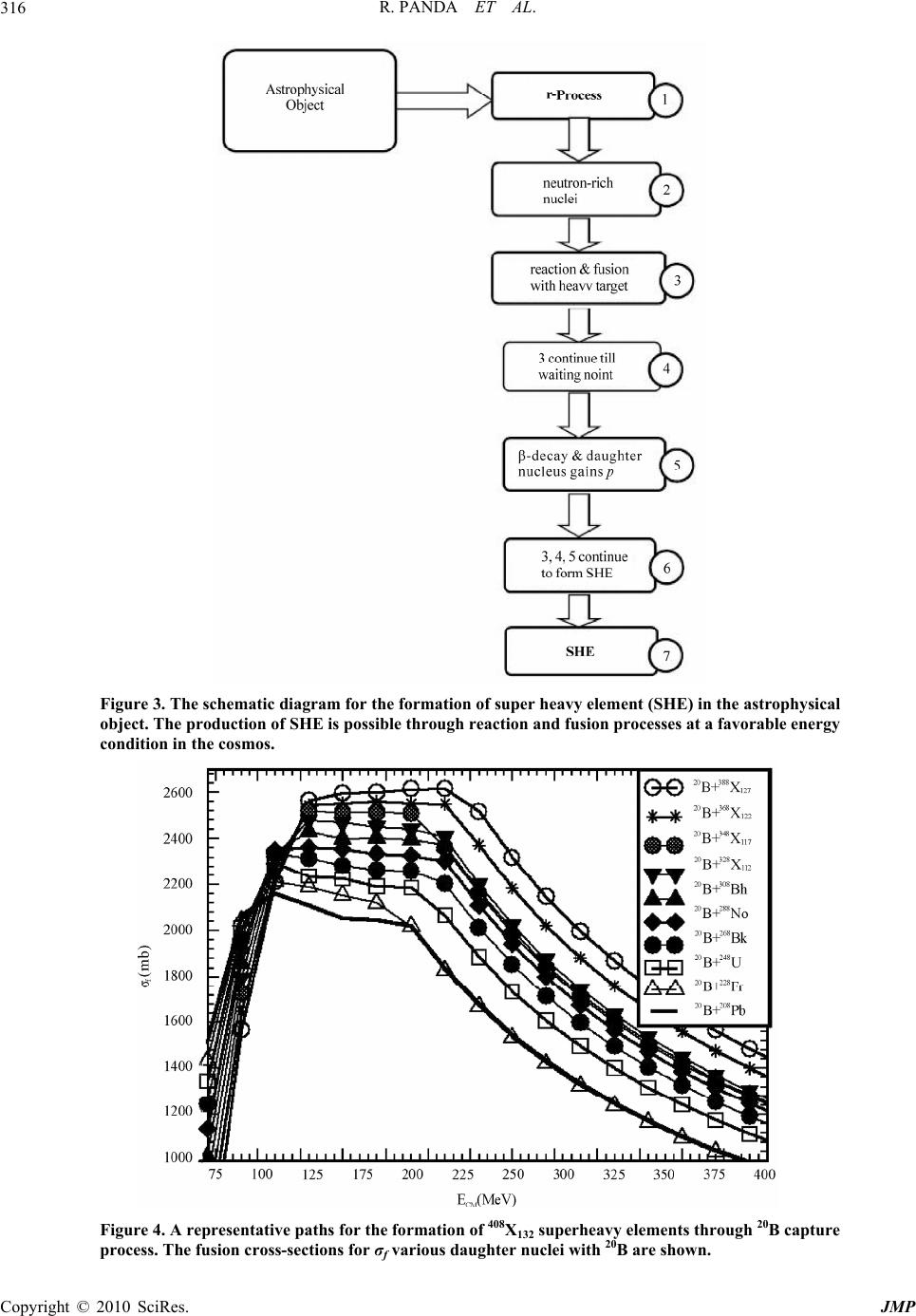

R. PANDA ET AL. 316
Figure 3. The schematic diagram for the formation of super heavy element (SHE) in the astrophysical
object. The production of SHE is possible through reaction and fusion processes at a favorable energy
condition in the cosmos.
Figure 4. A representative paths for the formation of 408X132 superheavy elements through 20B capture
process. The fusion cross-sections for σf various daughter nuclei with 20B are shown.

R. PANDA ET AL. 317
hancement in Z, the product (daughter nucleus) captures
few more n or neutron-rich light nuclei by fusion process
till it reaches the new waiting point. At this point, the
nucleus gains another proton p, by emitting β− particle.
This process continues and SHE or super-SHE is formed
in the cosmological object. In this context, it is worth
mentioning that, the dominant modes of decays are β− and
spontaneous fission for large N and large Z nuclei, re-
spectively. In the β− decay, the daughter nucleus gains a
proton, whereas for large N, the spontaneous fission re-
duces considerably due to excess number of neutrons [9]
and the neutron-rich isotope becomes fission stable as the
height of the fission barrier decreases and the width in-
creases, thereby making the nucleus more stable against
fission [9]. It is interesting to mention here that, recently it
has been reported by A. Marinov et al. [42,43], that the
evidence of a super heavy isotope with Z = 122 or 124 and
a mass number A = 292; has been found in natural Th
using inductively coupled plasma-sector field mass spec-
trometry. The estimated half-life of this isotope is t1/2 ≥
108 years, comparable with the theoretical predictions
[3-7].
4. Summary and Conclusions
In summary, we estimated the reaction and fusion cross-
section of various combinations of light and heavy iso-
topes. We extended the calculations to exotic systems
taking into consideration the possibility of availing the rn-
process and the exotic nuclei capture processes in astro-
physical objects. The enhanced cross-sections with in-
crease of mass number for both the projectile and target
made it possible for the formation of the heavier neu-
tron-rich nuclei way beyond the normal drip lines pre-
dicted by the mass models. By the neutron or heavy ion
(light neutron-rich nuclei) capture process the daughter
nucleus becomes a super heavy element which may be
available somewhere in the Universe in super-natural
condition and can be possible to be synthesized in labo-
ratories. Here the stability of the neutron-rich SHE or
super-SHE against spontaneous fission arises due to
widening of the fission barrier because of the excess
number of neutrons.
5. Acknowledgements
Discussions with Professors K. Langanke, L. Satpathy
and C. R. Praharaj are gratefully acknowledged. We are
thankful to Prof. A. Abbas for a careful reading of the
manuscript. This work has been supported in part by
Council of Scientific & Industrial Research (No. 03 (1060)
06/EMR-II) as well as the project No. SR/S2/ HEP-
16/2005, Department of Science and Technology, Govt.
of India.
6. References
[1] Yu. Ts. Oganessian, et al., “Synthesis of the Isotopes of
Elements 118 and 116 in the 249Cf and 245Cm+48Ca Fu-
sion Reaction,” Physical Review C, Vol. 74, No. 4, 2006,
p. 044602.
[2] P. Moller and J. R. Nix, “Stability and Decay of Nuclei at
the End of the Periodic System,” Nuclear Physics A, Vol.
549, No. 1, 1992, pp. 84-102.
[3] S. G. Nilsson, et al., “On the Spontaneous Fission of
Nuclei with Z near 114 and N near 184,” Nuclear Physics
A, Vol. 115, No. 3, 1968, pp. 545-562.
[4] S. G. Nilsson, et al., “On the Nuclear Structure and Sta-
bility of Heavy and Superheavy Elements”, Nuclear
Physics A, Vol. 131, No. 1, 1969, pp. 1-66.
[5] M. Brack, J. Damgaaid, A. S. Jensen, H. C. Pauli, V. M.
Strutinsky and C. Y. Wong, “Funny Hills: The Shell-
Correction. Approach to Nuclear Shell Effects and Its
Applications to the Fission Process,” Reviews of Modern
Physics, Vol. 44, No. 2, 1972, pp. 320-405.
[6] E. O. Fiset and J. R. Nix, “Calculation of Half-Lives for
Superheavy Nuclei,” Nuclear Physics A, Vol. 193, No. 2,
1972, pp. 647-671.
[7] J. R. Nix, “Calculation of Fission Barriers for Heavy and
Superheavy Nuclei,” Annual Review of Nuclear Science,
Vol. 22, 1972, pp. 65-120.
[8] A. Ozawa, T. Suzuki and I. Tanihata, “Nuclear Size and
Related Topics,” Nuclear Physics A, Vol. 693, No. 1-2,
2001, pp. 32-62.
[9] L. Satpathy, S. K. Patra and R. K. Choudhury, “Fission
Decay Properties of Ultra Neutron-Rich Uranium Iso-
topes,” PRAMANA-Journal of Physics, Vol. 70, No. 1,
2008, pp. 87-99.
[10] R. J. Furnstahl, B. D. Serot and H. B. Tang, “Analysis of
Chiral Mean-field Models for Nuclei,” Nuclear Physics A,
Vol. 598, No. 4, 1996, pp. 539-582.
[11] R. J. Furnstahl, B. D. Serot and H. B. Tang, “A Chiral
Effective Lagrangian for Nuclei,” Nuclear Physics A, Vol.
615, No. 3-4, 1997, pp. 441-482.
[12] B. D. Serot and J. D. Walecka, “Recent Progress in
Quantum Hydrodynamics,” International Journal of
Modern Physics E, Vol. 6, No. 4, 1997, pp. 515-631.
[13] R. J. Furnstahl and B. D. Serot, “Parameter Counting in
Relativistic Mean-field Models,” Nuclear Physics A, Vol.
671, No. 1-4, 2000, pp. 447-460.
[14] R. J. Glauber, “Lectures on Theoretical Physics,” In: W. E.
Brittin and L. C. Dunham, Eds., Interscience, Vol. 1, New
York, 1959, p. 315.
[15] P. Shula, “Glauber Model and the Heavy ion Reaction
Cross Section,” Physical Review C, Vol. 67, No. 5, 2003,
p. 054607.

R. PANDA ET AL. 318
[16] M. Y. H. Farag, “Modified Glauber Model for the Total
Reaction Cross-section of 12C + 12C Collisions,” European
Physics Journal A, Vol. 12, No. 4, 2001, pp. 405-411.
[17] S. K. Charagi and S. K. Gupta, “Coulomb-modified
Glauber Model Description of Heavy-Ion Reaction Cross
Sections,” Physical Review C, Vol. 41, No. 4, 1990, pp.
1610-1618.
[18] S. K. Charagi, “Nucleus-Nucleus Reaction Cross Section
at Low Energies: Modified Glauber Model,” Physical
Review C, Vol. 48, No. 1, 1993, pp. 452-454.
[19] S. K. Patra, R. N. Panda, P. Arumugam and R. K. Gupta,
“Nuclear Reaction Cross Sections of Exotic Nuclei in the
Glauber Model for Relativistic Mean Field Densities,”
Physical Review C, Vol. 80, No. 6, 2009, p. 064602.
[20] A. Shukla, B. K. Sharma, R. Chandra, P. Arumugam and S.
K. Patra, “Nuclear Reaction Studies of Unstable Nuclei
Using Relativistic Mean Field Formalisms in Conjunction
with the Glauber Model,” Physical Review C, Vol. 76, No.
3, 2007, p. 34601.
[21] B. K. Sharma, et al., “Reaction Cross-Sections for Light
Nuclei on 12C using Relativistic Mean Field Formalism,”
Journal of Physics G: Nuclear Particle Physics, Vol. 32,
No. 11, 2006, pp. 2089-2097.
[22] M. D. Estal, M. Centelles, X. Vinyas and S. K. Patra,
“Pairing Properties in Relativistic Mean Field Models
Obtained from Effective Field Theory,” Physical Review
C, Vol. 63, No. 4, 2001, p. 044321.
[23] S. K. Patra, M. D. Estal, M. Centelles and X. Vi˜nas,
“Ground-State Properties and Spins of the Odd Z = N + 1
Nuclei 61Ga-97In,” Physical Review C, Vol. 63, No. 2,
2001, p. 024311.
[24] B. A. Ibrahim, Y. Ogawa, Y. Suzuki and I. Tanihata,
“Cross Section Calculations in Glauber Model: I. Core
Plus One-nucleon Case,” Computer Physics Communica-
tions, Vol. 151, No. 3, 2003, pp. 369-386.
[25] K. Hagino, N. Rowley and A. T. Kruppa, “A Program for
Coupled-channel Calculations with All Order Couplings
for Heavy-Ion Fusion Reactions,” Computer Physics
Communications, Vol. 123, No. 1-3, 1999, pp. 143-152.
[26] L. H. Bradt and B. Peters, “The Heavy Nuclei of the Pri-
mary Cosmic Radiation,” Physical Review, Vol. 77, No. 1,
1950, pp. 54-70.
[27] S. Barshay, C. B. Dover and J. P. Vary, “Nucleus-nucleus
Cross Sections and the Validity of the Factorization Hy-
pothesis at Intermediate and High Energies,” Physical
Review C, Vol. 11, No. 2, 1975, pp. 360-369.
[28] S. Barshay, C. B. Dover and J. P. Vary, “The Validity of
the Factorization Hypothesis for Nucleus-nucleus Cross
Sections at High Energies,” Physics Letters B, Vol. 51, No.
1, 1974, pp. 5-8.
[29] A. Ingemarsson and M. Lantz, “Geometrical Aspects of
Reaction Cross Sections for 3He, 4He, and 12C Projec-
tiles,” Physical Review C, Vol. 67, No. 6, 2003, p.
064605.
[30] A. Ingemarsson and M. Lantz, “Energy Dependence of
Proton-Nucleus Reaction Cross Sections,” Physical Re-
view C, Vol. 72, No. 6, 2005, p. 064615.
[31] C.-T. Liang, Y.-A. Luo, X.-H. Li and C.-H. Cai, “Sys-
tematic Analysis of the Reaction Cross Section for d, 3He
and 4He as Projectiles,” Journal of Physics G: Nuclear
Particle Physics, Vol. 36, No. 1, 2009, p. 015102.
[32] H. P. Wellisch and D. Axen, “Total Reaction Cross Sec-
tion Calculations in Proton-nucleus Scattering,” Physical
Review C, Vol. 54, No. 3, 1996, pp. 1329-1332.
[33] J. Y. Hostachy, et al., “Elastic and Inelastic Scattering of
12C Ions at Intermediate Energies,” Nuclear Physics A,
Vol. 490, No. 2, 1988, pp. 441-470.
[34] V. Bernard, et al., “Production of Charged Pions in In-
termediate-Energy Heavy-Ion Collisions,” Nuclear Phys-
ics A, Vol. 423, No. 3, 1984, pp. 511-524.
[35] J. N. De, X. Vinyas, S. K. Patra and M. Centelles, “Nu-
clei beyond the Drip Line,” Physical Review C, Vol. 64,
No. 5, 2001, p. 057306.
[36] P. A. Mazzali, et al., “A Neutron-star-Driven X-ray Flash
Associated with Supernova SN 2006aj,” Nature, Vol. 442,
No. 7106, 2006, pp. 1018-1020.
[37] T. A. Thompson, P. Chang and E. Quataert, “Magnetar
Spindown, Hyper-energetic Supernovae, and Gamma Ray
Burst,” Astrophysics Journal, Vol. 611, No. 1, 2004, pp.
380-393.
[38] P. O. Lagage and C. J. Cesarsky, “The Maximum Energy
of Cosmic Rays Accelerated by Supernova Shocks,” As-
tronomy and Astrophysics, Vol. 125, No. 2, 1983, pp.
249-257.
[39] J. R. Wilson and R. W. Mayle, “Report on the Progress of
Supernova Research by the Livermore Group,” Physics
Reports, Vol. 227, No. 1-5, 1993, pp. 97-111.
[40] B. S. Meyer, “The r-, s-, and p- Process in Nucleosynthe-
sis,” Annual Review of Astronomy and Astrophysics, Vol.
32, 1994, pp. 153-190.
[41] J. M. Pearson, “Nuclear Physics: Energy and Matter,” Ch.
II, Adam Hilger Ltd, 1986, p. 87.
[42] A. Marinov, et al., “Evidence for the Possible Existence
of Long-lived Superheavy Nucleus with Atomic Mass
Number A = 292 and Atomic Number Z ≈ 122 in Natural
Th,” International Journal of Modern Physics E, Vol. 19,
No. 1, 2010, pp. 131-140.
[43] S. K. Patra, M. Bhuyan, M. S. Mehta and R. K. Gupta,
“Superdeformed and Hyperdeformed States in Z = 122
Isotopes,” Physical Review C, Vol. 80, No. 3, 2009, p.
034312.