J. Software Engineering & Applications, 2010, 3, 1067-1079
doi:10.4236/jsea.2010.311126 Published Online November 2010 (http://www.SciRP.org/journal/jsea)
1067
A Tile Logic Based Approach for Software
Architecture Description Analysis
Aïcha Choutri1, Faiza Belala1, Kamel Barkaoui2
1LIRE Laboratory, University Mentouri of Constantine, Constantine, Algeria; 2CEDRIC, Conservatoire National des Arts et
Métiers, Paris, France.
Received July 13th, 2010; revised August 31st, 2010; accepted September 3rd, 2010.
ABSTRACT
A main advantage of Architecture Description Languages (ADL) is their aptitude to facilitate formal analysis and veri-
fication of complex software architectures. Since some researchers try to extend them by new techniques, we show in
this paper how the use of tile logic as extension of rewriting logic can enforce the ability of existing ADL formalisms to
cope with hierarchy and composition features which are more and more present in such software architectures. In or-
der to cover ADL key and generic concepts, our approach is explained through LfP (Language for rapid Prototyping)
as ADL offering the possibility to specify the hierarchical behaviour of software components. Then, our contribution
goal is to exploit a suitable logic that allows reasoning naturally about software system behaviour, possibly hierarchi-
cal and modular, in terms of its basic components and their interactions.
Keywords: Tile Logic, LfP Model, Software Architecture, Hierarchical Composition
1. Introduction
Software Architecture (SA) has emerged as a principle
method of understanding and developing high level
structures of complex software systems. Nowadays, SA
artifacts are becoming the foundation for building
families of such systems. Then, the problem of ensuring
as early as possible the correctness of an SA occupies
increasing importance in the development life-cycle of
software products. Formal approaches should be used to
describe software architectures and express their dynamic
evolution so that one could reason on them.
Over past two decades there has been considerable
research devoted to modeling and analysis of software
architectures; among other, architecture description
languages (or ADL) as suitable notation for SA formal
specification. Their common advantage is their impressive
body representation of evidence about the utility of
architectural modeling and analysis [1]. Some of them
attempted to provide behavioral modeling and analysis
via numerous complementary behavioral formalisms.
However, the most of applied approaches share the goal
of defining mismatches in component composition.
Recently, some researchers in industry and academia
try to extend these ADL, by new techniques to analyze
and validate architectural choices, both behavioral and
quantitative, complementing traditional code-level analysis
technique [2].
According to this motivation, we show through this
paper how the tile logic as extension of rewriting logic
can support ADL artifacts allowing and enforcing formal
reasoning on software system behavior and dynamics. In
particular, we show that tile system is closely joined to
important inherent aspects of ADL, especially hierar-
chical behavior of components and compositional one.
We explain our proposed approach concretely through
LfP architecture description language [3] as ADL offering
the possibility to specify the hierarchical behavior of soft-
ware components (in terms of LfP-BD diagrams) in
addition to their structure that can be also of hierarchical
nature (LfP-AD).
Tile Logic [4] has been introduced for modular
description of open, distributed and interactive systems. It
constitutes a rewriting logic [5] extension taking into
account rewriting with side effects and rewriting
synchronization. So, it supports modular specification of
concurrent system behaviors, their interaction and
synchronization semantics thanks to its particular rules of
rewrite called tiles. These rules can be instantiated with
special terms in a given context. The main idea behind this

A Tile Logic Based Approach for Software Architecture Description Analysis
1068
logic is to impose dynamic restraints on terms to which a
rule may be applied by decorating rewrite rules with
observations ensuring synchronizations and describing
interactions.
Authors of [6,7] have proposed a mapping approach of
LfP architectural description into rewriting logic in order
to formalize its semantics and exploit this latter for
hierarchical verification of some properties using model
checking. The interest of such approach is the well care
in purely formal way of concurrency in a distributed
configuration through executable specification.
In this paper, we use Tile logic strength the results
obtained in [6,7] related to formalization and verification
of LfP software architecture description via rewriting
logic and its Maude language. Hence, owing to tile logic
elements, we can deal with and preserve naturally the
hierarchical structure and the hierarchical behavior of
SA. Besides, executable specification of tile systems
may be naturally defined by mapping tile logic into
rewriting logic which is a semantic basis of several
language implementations. In particular the proposed
model implementation requires developing a set of
strategies to control rewriting by discarding compu-
tations that do not correspond to any deduction in tile
logic.
In the remainder of this paper, Section 2 situates our
work among analogous ones in order to better surround
its problematic. Section 3 is devoted to summarize basic
concepts of tile logic. In Section 4, we present our
approach to map an architectural description into tile
logic. It is then explained and illustrated in Section 5
through LfP language. So, a successful classic case study
of Producer/Consumer system is considered to show how
we proceed to clutch tile logic to software architecture
description language. Some comments evaluating our
contribution are presented in Section 6. Last section
concludes our work and gives its perspectives.
2. Contribution Setting
It is not a novel idea to give a formal specification for
software architecture. Most of existing ADL concentrates
on providing a precise mathematical semantics for
software architecture description of a system. All well
known semantic formalisms for ADL give limitation
when software architectures deal not only with structural
aspects but also with behavioral ones. Besides, hierarchy
concept, synchronization and reconfiguration ones
restrict the use of these ADL formalisms. In the case of
Rapid [8] for example, based on POSets (Partially
Ordered event Sets), only architectural components
interactions are formalized in addition to the architectural
elements. Also, Wright [9] uses a subset process algebra
named CSP (Communicating Sequential Processes)
formal notation to describe partially components abstract
behavior in a simple manner. Recent related works focus
on defining rewriting logic based model for some
existing ADL. For example, authors in [10] define a
mapping of CBabel concepts into rewriting logic. A
particular attention has been given to specify syntactic
constructs semantic of this ADL example. LfP [3]
integrating UML notations and state/transition automaton
has been considered by the work of to associate to each
of its views (LfP-AD and LfP-BD diagrams) possibly
hierarchical an appropriate semantic meaning based on
rewriting logic too. In fact, rewriting logic has been
recognized as a semantic framework to model software
system architecture. However, complexity of such
systems structure and behavior induces rewriting logic
flat models that do not preserve compositional and
hierarchical features of ADL, so they are often difficult to
manage. In this paper, we will show that tile logic based
model, even if it is more complex to grasp, is much more
appropriate and efficient.
Tile logic is an extension of rewriting logic, supporting
modular description of concurrent system behaviors, and
their interaction and synchronization semantics. These
assets delegate it as being the most suitable formalism to
support semantic of more complex ADL, namely those
having the possibility to describe hierarchical and mo-
dular specification of distributed and open architectural
applications such as LfP descriptions.
In particular, both static and dynamic views of LfP
architecture are naturally translated according to the tile
system structure (space), and its computation flow (time),
preserving hierarchical and compositional nature of this
architectural description. Furthermore, this tile model
may be then successfully exploited to formal reasoning
on such descriptions and their analysis.
3. Tile Logic
In this section, we recall some fundamental concepts of
the underlying semantic framework, namely tile logic.
More interested readers may consult [4].
Tile Logic has been introduced for modular description
of open, distributed and interactive systems. This
formalism reminiscent to term rewriting and concurrency
theory, constitutes a rewriting logic [5] extension taking
into account rewriting with side effects and rewriting
synchronization. Although, ordinary format of rewrite
rules allows state changes expression and concurrent
calculus in a natural manner, it lacks tools to express
interactions with the environment, i.e., rewrite rules can
be freely instantiated with any term in any context. The
main idea behind tile logic is to impose dynamic
restraints on terms to which a rule may be applied by
decorating rewrite rules with observations ensuring
C
opyright © 2010 SciRes. JSEA

A Tile Logic Based Approach for Software Architecture Description Analysis
1069
synchronizations and describing interactions. gory, the superposition of these two categories of cells
The obtained rules are then called tiles, defining the
behavior of partially specified components, called
configurations, in terms of actions related to their input
and output interfaces (the possible interactions with the
internal/external environment).
Each tile, having one of the forms in Figure 1, ex-
presses that initial configuration s evolves to the final
configuration t via the tile
 , producing the effect b,
which can be observable by the rest of the system. Such a
rewriting local step is allowed, only if the sub-compo-
nents of s (its arguments) evolve to the sub-components
of t producing an effect a, which acts as a trigger for α
application.
Arrows s and t of the tile α (in Figure 1) are called
configurations (system states). They are algebraic
structures equipped with operations of parallel and
sequential composition. Each system configuration has
both input and output interfaces responsible of system
interactions with the environment.
,
ould be considered as a natural model for tile system.
x, y the
in t interfaces and, w, z the output interfaces.
on-
fig
4. Tile Logic for Architecture Description
and an internal behavior, specified by a set of tiles, to
sh
Definition 1. A tile system is a 4-tuple T = (H, V, N, R)
where H, V are monoïdal categories with the same set of
objects OH = OV, N being a set of rule names and R:
N→ H x V x V x H a function where for each α in N, if
R(α) = (s, a, b, t), then s:x
 y, a:x  w, b:y  z and t:
w  z, for suitable objects x, y, z and w; with
pu
Auxiliary tiles set may be necessary to specify consis-
tent interfaces rearrangements. A standard set of infer-
ence rules (Figure 2) allows building larger rewriting
steps, by composing tiles freely via horizontal (through
side effects), vertical (computational evolution of c
uration) and parallel (concurrent steps) operations.
In the recent literature, tiles representing an extension
of the SOS specification approach are designed for deal-
ing with open states. They seem apt for many current
applications [11-13]. Indeed, they have been used with
success to model in detail several application classes such
as coordination languages (triggers and effects represent
coordination protocols) and software architecture styles
[13,14]. This paper contributes to another meaningful and
interesting application of Tile logic, it generalizes the
approach proposed in [15] by defining a common formal
Arrows a and b decorating tile α (in Figure 1) are also
algebraic structures, they define observable effects
(actions) for coordinating local rewrites through confi-
guration interfaces (input and output ones).
In general, configurations and observations give rise to
two categories having the same class of objects (inter-
faces). The former (horizontal so-called configuration)
defines effects propagation; the latter (vertical so-called
observations) describes state evolution. Then, double cate- model based on tile logic for architecture descriptions.
Languages
Tile logic has been exploited as a common semantic
framework to define both abstract software architectures
and their behaviors [16]. Generally, each component in a
distributed system specification is described by a set of
external ports, ensuring interactions with the environment
or :a
b
st  
x y
a  b
w z
s
t
x, y: initial and final input interfaces
w, z: initial and final output interface
Figure 1. A tile representation.
Rules generating the basic tiles, horizontal and vertical identities:
R()=(s,a,b,t)
:a
t :x  y H
:Hx id tt
y
a : x  z

V
:Va id xz
a
s
t
b







Horizontal, vertical and parallel compositions
: :
ab
s
th f
bc
 
: ; ;
a
s
htf
c
 
a
:st :t
b
ch
d



;
: ;
ac
::
ac
s
th f
bd



: sac htf
bd

s
h
bd
 





Figure 2. Inference rules.

A Tile Logic Based Approach for Software Architecture Description Analysis 1070
a deliver component functionalities. It is define
cess and Fundamental
SincDL, a complete software architectur
that could be eithe
co
ociated mainly to
(internal) description given by a tile
ng, we present the four essential steps o
til
tep 1: Each software architectural Config ura tion in-
rizontal and vertical categories are formed (see
tion) that are
ded/required
ting hidden sub components
model Configura-
tiTS for a given architectural configuration Con-
ntation deduced from their partial description.
gCset, MsgCget provided
computation component name with a
at formalize
s
(1)
(2)
d by a tile tion. Its ho
system, where objects of the two categories correspond to
component interfaces. Vertical category (observations)
defines its possible actions corresponding to component
required/provided services and horizontal category gen-
erates all component possible configurations. Gathered
together via a set of tiles, horizontal and vertical catego-
ries define expected behavior of the underlying compo-
nent. Starting from a basic set of tiles and deduction rules
of this logic, system global behavior defined as a coordi-
nated evolution of its subcomponents, is naturally de-
duced. We take in what follows all these ideas formulated
through a generic semantic framework applicable for
ADL either their semantics. It will be then applied on a
specific case study.
4.1. Modeling Pro
Definitions
e in existing Ae
tiles formalize binding connection. Some auxiliary
tiles may be added to these basic tiles in order to
deal with some particular ADL connection aspects
like dynamic connection (components synchroni-
zation) as it is the case for parameterized dynamic
connection tiles defined in [16].

Definition 2. A tile system based
description has to consider static architectural configura-
tion and dynamic evolution (behavior) of software system,
our proposed model follows the same separation of con-
cerns. Two distinct, but not completely independent
views are considered. For the first one, expressed by a set
of existing components, connectors (often considered as
particular components) and connection topology, we
associate a tile system integrating these components (and
connectors) definitions. In the second view, state transi-
tion system, which is usually devoted to define compo-
nent and system behavior, is extended and formally de-
fined in the context of tile logic.
Then, a software component,r a connection points.
 Morphisms of VConf-TS are simplified to design only
two types of services: Ms
mputation component or a connector, may have two
definitions according to its granularity:
 A partial (external) description, ass o
its interface, evolving an abstract data type for each
component type (sort, operations and their pro-
perties).
 A detailed c
system formalizing both structure and behavior
component. Computation or storage component may
be either primitive or composite. For later case, the
associated tile system is a composition of a set of
hierarchical sub tile systems. If the component is a
connector (communication entity), the associated tile
system defines the corresponding communication
protocol.
In the followif
binding connection deduced from configuration
topology-connection. Two general forms of tiles can
be defined here:
1'
12 :
MsgC set
CC s
e model generation for any software architecture
description:
S
volves an associated tile system Configuration–TS defini-
Definition 2) by the involved architectural elements
(components, connectors, ports, etc.).
 Morphisms of the horizontal category formalize
connection points (in Configura
characterized by essentially components names and
interfaces, in terms of algebraic terms.
 On the other hand, morphisms of the vertical
category (observations) formalize provi
components services.
 Both categories have the same set of objects that are
algebraic terms represen
models that will be described at the next lower level.
 The set of tiles expresses configurations evolution
and its propagation over all sub-components. These
on-
figuration = (Components, toplogy-connection) is de-
fined by the 4-tuple (HConf-TS, VConf-TS, NConf-TS, RConf-TS)
such that:
 OConf-TS is composed of all components abstract
represe
 Morphisms of HConf-TS are formed upon algebraic
terms specifying component interfaces intervening in
r required by a component of name C under a
message form.
 NConF-TS is the set of tile names. Each one is obtained
by combining a
ommunication component name. If there is no
explicit connector (i.e., case of dynamic connector),
the second name will be that of other computation
component connected to the first one.
 RConf-TS: NConf-TS → H
Conf-TS × VConf-TS
 VConf-TS
 HConf-TS is a function defining tiles th
1 1
2 MsgC get

2'
23 22
3
:MsgCget CC ss
MsgC set

C
opyright © 2010 SciRes. JSEA

A Tile Logic Based Approach for Software Architecture Description Analysis 1071
s1, s1’, s2, s2’ are configurations, i.e. morphisms of
HConf-TS, C1, C3 are computation com
C2 is a connector name and MsgC1set, MsgC2get

Step
prese
articular tile system (Definitions 3 and 4).
uration-TS
of any ADL architecture de
ription, is defined in the same way as for configu
tion 4) is conceived on the
onent software architecture de-
ribed by a given state transition system with respect to
s.
is the set of tile names. Each one is
formalize all tran-
label transition and identity morphism respectively
while t-TS-trigger denotes transition
as trigger for hidden transition tile system.

mpu-
nt may be hierarchical, they
he other sub state transition systems. So, recursively we
It is clear that our approach for defining a formal
general as it provides concise and complete se-
m
scribing
tructuring aspects of a SA. It is re-
ving characteristics of a coordi-
e style of components as-
mplementary views
e
ponent name, 
are possible observation, i.e. morphisms of Hconf-TS.
2: For each computation component type in the
nt software architecture configuration, we associate
s
a p
 If it is the case of a composite computation
component (Composite-Component), then the tile
system in question Component-Config
(Definition 3) formalizes its architectural configu-
ration and has the same definition of Configu-
ration-TS. Hence, it is necessary to perform all the
process steps while adopting appropriate notations to
avoid any confusion.
Definition3. Tile system Composite-Component-TS mod-
eling composite component-
scra- tation component.
Step 3: Since transitions in the state/transition model that
describes primitive compone
tion-TS, by the 4-tuple (HCompCConf-TS, VCompCConf-TS,
NCompCConf-TS, RCompCConf-TS).
 If the software component is primitive (Primitive-
Component), its associated tile system Primitive-
Component-TS (Defini
basis of state transition system elements which is
usually used to describe the component behavior.
The set of common objects of its both categories
(horizontal and vertical) is composed of all
elementary architectural elements of the component
like attributes, ports, constraints, or other eventual
annotations. Horizontal (configurations) category
formalizes in this case component states, vertical
(observations) one specifies all its possible transition
triggers given in terms of labels. Two general tile
forms are then defined for either simple transition or
hierarchical one.
Definition4. Tile system Primitive-Component-TS mod-
eling a primitive comp
sc
a given ADL, is defined by the 4-tuple (HPrimComponent-TS,
VPrimComponent-TS, NPrimComponent-TS, RPrimComponent-TS) such that:
 OPrimComponent-TS is composed of algebraic terms
associated to all architectural elements of the
component.
 Morphisms of HPrimComponent-TS are formed upon
algebraic definitions of states in terms of well
defined tuple
 Morphisms of VPrimComponent-TS are formed upon
algebraic definitions of all existing transition labels.
 NPrimComponent-TS
ither a transition name or defined to formally
identify an unnamed transition.
RPrimComponent-TS: NPrimComponent-TS → H
PrimComponent-TS ×
VPrimComponent-TS  VPrimComponent-TS  HPrimComponent-TS is
the function defining tiles that
itions.
Two general tile forms are proposed for either simple
(tile3) or hierarchical (tile4) such as l and id denote
:1 s2
l
ts idH  (3)
:1 l ts tTStrigge 
 s2 r
 (4)
effect that acts
Finally, If the component is a communication one
(Communication-Component), its tile system model
is defined in the same way as for primitive co
id
associate to each hierarchical transition, at the next lower
level, a novel tile system as we have proceed in the pre-
vious step.
Step 4: Step 3 is repeated until all transitions become
simple.
model based on tile logic for any ADL is quite generic
and too
antics definitions for all important common ADL con-
cepts, mainly the hierarchy. Indeed, this may reduce con-
siderably the semantic gap between ADL noted before.
We will show through the instantiation of this modeling
process to the LfP language case, that the resulting model
covers entirely and naturally its formal semantics while
preserving its modular and hierarchical structure. There-
fore, we resolve the usual problem (flat model) still posed
in previous ADL formalization approaches (such as those
based on Petri nets and rewriting logic models).
4.2. Case of LfP
LfP (Language for Prototyping) [2,16] allows de
both control and s
garded as a language ha
nation language and an ADL.
4.2.1. LfP Software Architecture
LfP, like all other ADL, provides a concrete syntax to
describe SA with a declarativ
sembly. It offers two distinct and co
C
opyright © 2010 SciRes. JSEA

A Tile Logic Based Approach for Software Architecture Description Analysis
1072
finition, their links and all system global decla-
rat
d execution flow belonging to LfP class
or
s, a guard or a post con-
di
ar
Model for LfP
ically basic LfP methodology
to LfP lan-
gu
e all concentrated on Petri nets formalism in order to
use their well known analysis tools. But in practice, these
models have already proved their insufficiencies. Indeed,
the hierarchical behavior greatly expressed in LfP com-
ponents is not preserved by this translated model and
even those based on rewriting logic, recently introduced
by [5,6].
4.2.2. Tile
to allow a complete description of software system. Ar-
chitectural view uses LfP-AD diagram to define system
architectural configuration and its components, behav-
ioral view specification deals with system dynamic be-
havior in terms of hierarchical behavior diagrams:
LfP-AD. LfP constructs are well defined in [17]. In what
follows, we recall the most used ones in our approach
context.
Architecture diagram (LfP-AD): It is LfP static model
description defining the participating components to a
system de
Figure 3 summarizes graph
defined in [3] to which our approach (bold part) is trans-
planted as a new possible alternative formal semantic
model emphasizing both software system compositional
behavior and hierarchical one. LfP software architecture
description is naturally translated into set of tile systems.
Each tile system allows the formal specification of an LfP
software component (LfP-AD, class, class instance, me-
dia) or sub-component one (methods, block transitions)
including the declaration of their constraints.
The proposed generic model is instantiated
ions. More precisely, LfP-AD describes system soft-
ware architecture as a graph whose nodes are the soft-
ware entities (LfP classes) and their link edges are com-
munication entities (LfP media). The interaction point’s
connection (LfP ports) allows these entities to be assem-
bled. Any connection has to respect binding contracts
(LfP binders).
Behavior diagram (LfP-BD): it specifies LfP class be-
havior, or a communication protocol associated to LfP
media or a metho
age with respects to its methodology different views
(Functional, properties and implementation). This will
help us then to give more precise and complete definition
of all different LfP architectural elements semantics in
Tile logic based framework. Besides, executable specifi-
cation of this new LfP model may be naturally defined by
mapping [18,19] tile logic into rewriting logic which is a
semantic basis of Maude language [20] and will extend
the proprieties view in LfP methodology, by the specifi-
cation and formal analysis of other behavior constraint
kinds, strongly related to LfP features (synchronization,
hierarchical behavior, etc.). Therefore, we apply to LfP
software architecture description, the construction tile
model process presented previously, step by step while
highlighting the hierarchy preservation.
LfP media. Formally, this diagram type expresses
component (class or media) behavior through state/tran-
sition automaton. Communication between component
automatons is achieved by message queues. Since LfP
allows the description of hierarchical behaviors, two
types of transitions are defined in LfP-BD behavior
model: simple transitions and hierarchical ones (method
transitions, block transitions).
These latter, encapsulate other behaviors also ex-
pressed by sub-LfP-BD that may be reused. A transition
can be provided with annotation
tion which must be checked.
Research works around LfP semantics formalization
Figure 3. LfP methodology extension.

A Tile Logic Based Approach for Software Architecture Description Analysis 1073
Table 1. Mapping LfP Concepts into Tile Logic.
LfP elements Tile model elements
LfP-AD
Class
Media
Binder
Global declarations
LfP-AD-TS
Sub-sort of component sort
Sub-sort of component sort
Sorts, Configurations, Binder-tiles
Global definitions
Component LfP-BD
Local declarations
1. Class LfP_BD
States
Transition Name
Annotations, guards,
post-conditions
Simple transitions
Method transitions
Block transitions
Transition actions
2. Media LfP-BD
Similar to LfP-BD class
excep
and n
Component sort, Component-TS
Objects of horizontal and vertical catego-
ries
1. Class-TS
Configurations
Transition Name-Tile
Objects (interfaces or particular con-
figurations)
Simple-Transition-Tiles
Method-Tiles, Method-TS
Entailed Block-Tiles, Block-TS
Observations
2. Media-TS: Particular case of Class-TS
with Simple-Transition
t: no media type
o method transition
-Tiles only.
1 summarimost LfP
cts into tile logice model.
Ld M
sptecture
D) is
as ition 2, enriched
definitiation of global
declarations of the LfP-Aperations for
coninstis
not tiatedAD-TS , NAD-TS
RA
posed term
ng
se
ponent tile systems (Component-TS)
tions) formalize binders as they
AD-TS message sending
 NAD-TS is set of tile names. Each one is defined by
combining associated component and media names
or the reverse noted in general: B-CM, B-MC.
 RAD-TS: NAD-TS
 HAD-TS  VAD-TS  VAD-TS  HAD-TS is
a function to formalize binding contracts. For
synchronous case, each resulting tile has one of the
following forms with respect to general tiles (1) and
(2) defined in the tile model construction process.
Where:
Conf-BCM2 = binder-CM(c, p, m, i1, i2+1, synch, po),
Conf-BMC1 = binder-MC(m, c, p, i1, i2, synch, po),
Conf-BMC2 = binder-MC(m, c, p, i1, i2+1, synch, po),
c: class-name, p: port, m: media-name, i1and i2: inte-
ger that represent binder capacity and message number
respectively and po: policy.
For example, the tile B-CM expresses connection be-
tween any obj of a class c that sends a mssage
SubSort computeComponent, connector < component
Table zes the mapping of
oncep. It helps to dress the til
fP-AD Tile Baseodel (Step 1):
Architectural viewecified in LfP by an archi
s
diagram (LfP-Aformalized by a configuration tile
defisystem LfP-AD-TS
witobal
ned in Defin
onh gls as transl
D (sorts for types, o
stants and static ances). So, this Tile system
AD-TS
ed by the instan
D-TS tuple (H, V,
s
Operations
… : name, interface → component
NameC: component → name
InterfaceC: component → interface
) such as:
OAD-TS is com of component algebraic
defined accordi ts as presented in
terms are in fact abstraction of
o signature
(Figure 4). The
hierarchical com
 HAD-TS (configura
support the binding connection point’s semantics of
LfP components. Their definition is based on
signature given in (Figure 5).
 V (observations) formalize LfP
and receiving. Each one may have one of the
following form:
MsgCset: send message by class C.
MsgCget: receive message by class C.
Msg-Mget: receive message by a media M.
MsgMset: send message by media M.
ect
through its port
e
p and the media m which must perform
souting towards a receiving class object. This connec-it r
tion can be accomplished only during execution with
class and media instances, by horizontal composition
(synchronization) of this tile with: on the one hand, a
ner tile having MsgCset as effedect, and a media tile
having MsgMget as trigger, on the other hand. By analogy,
Sorts name, interface
Operations
… : string → name
(….,…): port, msg → interface
Sort component
Figure 4. Signatures for component algebraic definition.
Sort binder
Operations
Binder-CM: class-name, port, media-name, integer, integer,
mode, policy → binder
W
G: → policy
Binder-MC: media-name, class-name, port, integer, integer,
mode, policy → binder
here
-Arguments of integer sort correspond respectively to binder
storage capacity de and the number of messages.
-Sorts mode and policy are defined by:
Synch, Asynch: → mode
FIFO, LIFO, BA
Figure 5. Signature of bine.
g.C.set binder-CM(c, p, m, i1, i2, synch, po)
g.M.get
 (5)
Msg.M.set binder-MC(m, c, p, i1, i2+1, synch, po)
Msg.C.get
(6)
Ms
nch i1)Ms  B-CM : binder-CM(c, p, m, i1, i2, sy, po) (i2 <
B-MC : binder-MC(m, c, p, i1, i2, synch, po) (i2+1 < i1) 
C
opyright © 2010 SciRes. JSEA

A Tile Logic Based Approach for Software Architecture Description Analysis 1074
tile B-MC expresses a connection between media and
any receiving class instance.
LfP-Bl (Step 2):
Throuew, we generate Componen t- TS
tile syram defined by the tuple
(HComp , V, Nponent-TS, RComponent-TS) as
given would
be eithd con-
cise p primitive component
whichor.
 Osemantic elements
to
component architectural elements like attributes,
local declarations, or annotations defined in the
component LfP-BD.
 HComponent-TS (config uration s) formalizes states of the
underlined LfP-BD.
 VComposant- (observations) formalizes all transition
hod, perform block).
 NComponent-TS is the set of transition names.
nent-TS
 VComposant- TS
perator is Ä.
ms Method-TS and Bloc-TS
Block-TS, NBlock-TS, RBlock-TS) is de-
ion is
method-TS
defined in the underlined sub-LfP-BD in terms of
nsub LfP-BD specified in LfP architecture
d
5. ple Client-Server
T ge-
nerr
(CSple and show that tile
logic provides emantic frame-
work for LfP icular and for
any ADL in ge
5.1. CS LfP Model
The architectural view (LfP-AD) of our application
stated in Figure 6 contains three compon
classes “Client” and “Server” connected via a m
named “MsgPassing”. Connexion is represented by in-
terposing binders (messages queues with multiplicity
interaction semantics noted by annotations) at media
ation,
ex
gure 7).
Th
ur hierarchical transitions
ibes meth-
h
on (by two possible not detailed
xecution paths: transition methods exec and notify),
re-
s
(CS-AD-TS, Client-TS, Msg-Passing-TS, Server-TS, Start-TS,
→ 5
→ 1
D Tile Based Mode
gh behavioral vi
stem to each LfP-BD diag
nent-TS Component-TSComo
by Definition 4. Particularly, Component-TS
S or Media-TS and for simple an er Class-T
resentation we consider only
may have hierarchical behavi
Component-TS is composed of
expressed as algebraic terms that correspond
actions (from simple action to sequential compo-
sition of actions, call met
 RComponent-TS: NComponent-TS
 HCompo
 VComposant-TS  HComponent-TS is a function formalizing
transitions in terms of tiles having forms (3) or (4).
In any form of tile, initial configuration could be a
composition of initial transition state with eventual guards
or precondition, as well as final configuration could be a
composition of resulting transition state with eventual
post-condition. For both cases, the used o
Hierarchical T ran si tion Formaliz ati on (Step 3):
All tiles associated to LfP hierarchical transitions,
method transitions and bloc transitions, have to be in fact
entailed by sub tile syste
o
associated to the hidden sub-LfP-BD respectively.
Bloc-TS = (HBlock-TS, V
fined recursively in the same way as Component-TS
replacing component name by LfP block name.
But, the tile system defined for a method transit
given uple Method-TS = (Hmethod-TS, V
by the t,
Nmethod-TS, Rmethod-TS) such that:
 Omethod-TS is composed of semantic elements
associated to attributes and annotations.
 Hmethod-TS, Vmethod-TS and Nmethod-TS are defined in
similar way as for H
Component-TS, VComponent-TS and
NComponent-TS respectively.
 Rmethod-TS: NBD-TS

HBD-TS  VBD-TS  VBD-TS  HBD-TS TS
is a function formalizing only simple transitions as
tiles of form (3).
Step 4: Lastly, step3 must be repeated with respect to the
binding ports level.
We will present a part of the whole LfP specific
umber of
escription.
Case Study: Sim
Application
he aim of this section is to illustrate the proposed
ic semantic model concepts to a classical client-seve
) architectural application exam
ef
description language in part
fectively a powerful s
neral.
ents: two
edia
and
ample sufficient to deal with all architectural and be-
havioural LfP concepts mainly modular and hierarchical
ones. We only give server class behaviour (Fi
e corresponding LfP-BD defines concurrent execution
of actions requested by the client. It consists of three
states EGI, S1, END and foB N
init, start, worker and daemon.
The sub-LfP-BD (right of Figure 7) descr
ods and blocks invoked by various associated hierarchi-
cal transitions. As it is shown in the figure, we have pre-
sented hree sub-LfP-BDnly t. From top to bottom, te
first one describes the init method role by a simple tran-
sition T1 (pseudo code). Both other sub-LfP-BD describe
roles of block transitions worker (by a not detailed sim-
ple transition) and daem
e
respectively.
5.2. CS Tile Model
With respect to LfP definition instantiation given p
viously, we deduce a set of hierarchical tile system
init-TS, Daemon-TS, worker-TS,…) for our client-server
application following especially the proposed genera-
tion steps.
Step1:
Global definitions :
Opérations MaxClient:
MaxServeur:
CS-AD-TS = (HCS-AD-TS, VCS-AD-TS, NCS-AD-TS, RCS-AD-TS)
where:
C
opyright © 2010 SciRes. JSEA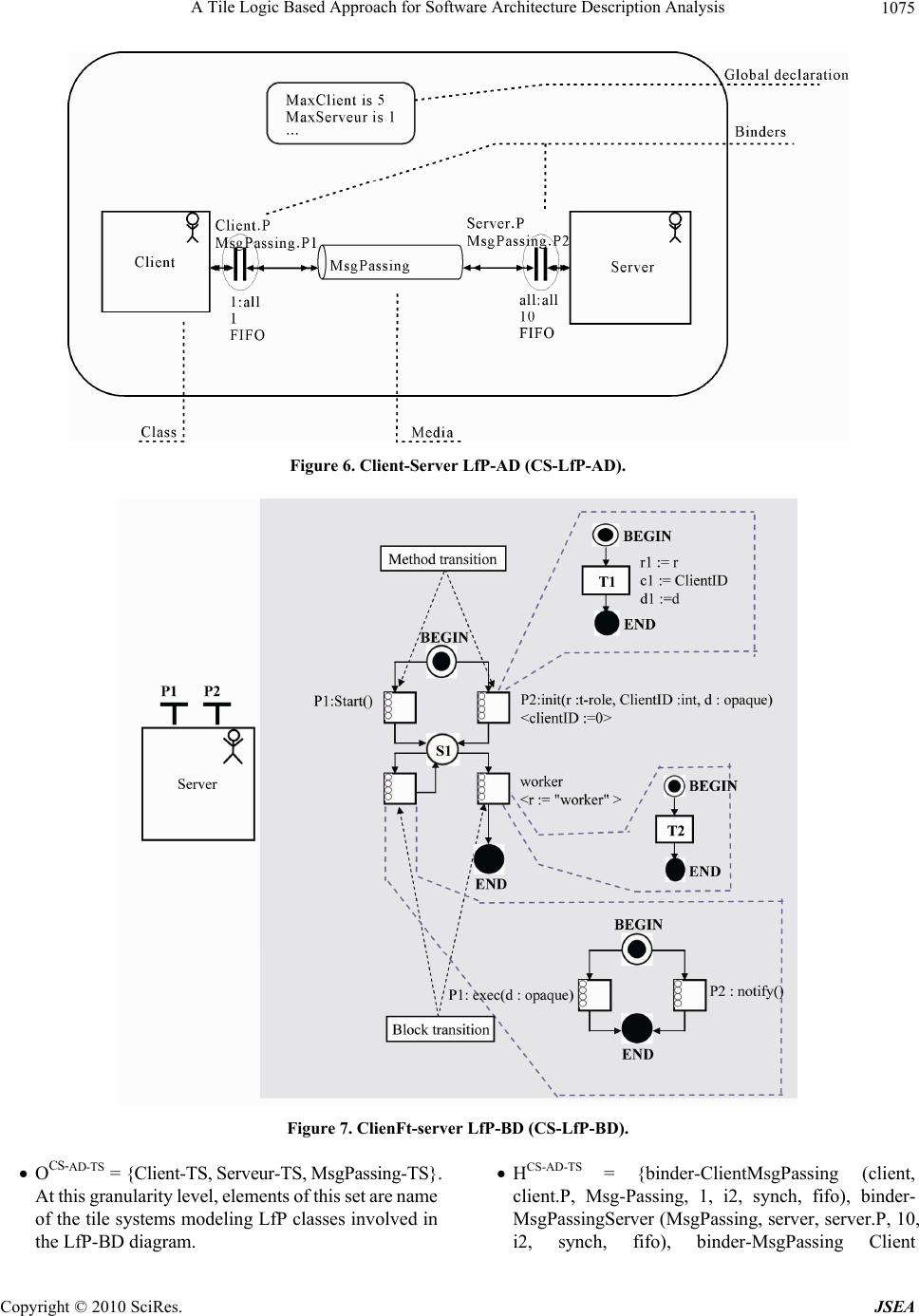

A Tile Logic Based Approach for Software Architecture Description Analysis 1075
S-LfP-AD). Figure 6. Client-Server L fP-AD (C
Figure 7. ClienFt-server LfP-BD (CS-LfP-BD).
 OCS-AD-TS = {Client-TS, Serveur-TS, MsgPassing-TS}.
At this granularity level, elements of this set are name
of the tile systems modeling LfP classes involved in
the LfP-BD diagram.
 HCS-AD-TS = {binder-ClientMsgPassing (client,
client.P, Msg-Passing, 1, i2, synch, fifo), binder-
MsgPassingServer (MsgPassing, server, server.P, 10,
i2, synch, fifo), binder-MsgPassing Client
C
opyright © 2010 SciRes. JSEA

A Tile Logic Based Approach for Software Architecture Description Analysis
1076
(Msg-Passing, client.P, client, 1, i2, synch, fifo),
binder-ServerMsgPassing (server, server.P,
MsgPassing, 10, i2, synch, fifo)}. All binder
declarations are considered by this configurations
category (objects of the category).
 VCS-AD-TS = {Msg-ServerGet, Msg-ServerSet, Msg-
ClientGet, Msg-MsgPassingGet, Msg-MsgPassing
Set}. Here all observable actions are summarized.
 NCS-AD-TS = {B-ClientMsgPassing, B-MsgPassingClient
B-MsgPassingServer, B-Server-Msgpassing}.
 RCS-AD-TS: NCS-AD-TS  H
CS-AD-TS  V CS-AD-TS 
VCS-AD-TS  HCS-AD-TS.
For synchronous case, we can define four basic tiles,
with RCS-AD-TS..
Msg-ClentS et
B-Client-MsgPassing: binder-ClientMsgPassing(P1)(21)Msg-MsgPassingGet
binder-ClientMsgPassing(P1')(21)
i
i

 

with:
P1 = (client, client.P, MsgPassing, 1, i2, synch, fifo) P1' = (client, client.P, MsgPassing, 1, i2+1, synch, fifo)
Msg-ServerSet
B-Server-MsgPassing: binder-ServerMsgPassing(P2)(210)Msg-MsgPassingGet
binder-ServerMsgPassing(P2')(210)
i
i

 

with:
P2 = (serveur, server.P, MsgPassing, 10, i2, synch, fifo) P2' = (serveur, server.P, MsgPassing, 10, i2+1, synch, fifo)
Msg-MsgPass ingSet
B-MsgPassing-Client: binder-MsgPassingClient(P3)(21)Msg-ClientGet
binder-MsgPassingClient(P3')(21)
i
i

 

With:
P3 = (MsgPassing, client, Msg-Passing.P, 1, i2, synch,
fifo)
P3' = (Msg-Passing, client, MsgPassing.P, 1, i2+1, synch,
fifo)
Msg-
: binder-MsgPassingServer(P4)(210)iMsgPassingSet B-MsgPassing-Server Msg-ServerGet
binder-MsgPassingServer(P4')(210)i

 

With:
P4 = (MsgPassing, server, MsgPassing.P, 10, i2, synch,
fifo)
P4' = (MsgPassing, server, MsgPassing.P, 10, i2+1,
synch, fifo)
For example, the tile B-ClientMsgPassing means that
starting from the configuration binder-ClientMsgPassing
(client, client.P, Msg-Passing, 1, i2, synch, fifo) of the
connection point between the Client and the media
MsgPassing, while the number i2 of messages in the
binder file is less than its capacity (equals to one), the
client can set its message (Msg-ClientSet trigger) and so,
the configuration evolves to binder-ClientMsgPassing
, client.P, MsgPassing, 1, i2+1, synch, fifo) while
g
oni-
zation of rewrites with a particular tile (having
Msg-MsgPassingGet as a trigger) to be defined into
MsgPassing-TS.
The tile B-MsgPassingServer means that starting from
nfiguration binder-MsgPassingServer (MsgPassing,
Msg-rverGet as a trigger) to be defined into
Server-TS.
By analogy, the meaning of both other tiles can be
easily deduced.
cal tile systems defined in the previous step a refined
model in terms of tile systems. As we have noted just the
server class LfP-BD is concerned by our approach illus-
tration. Its associated model is given by the following tile
ystem:
(client
i2 will be incremented. The final effect of this rewritin
(Msg-MsgPassingGet) is necessary to ensure synchr
the co
server, server.P, 10, i2, synch, fifo) of the connection
point between the media Msg-Passing and the Server,
while the number i2 of messages in the binder file is less
than its capacity (equals to 10), the media can set a mes-
sage received from the Client (Msg-MsgPassingSet
trigger) and so, the configuration evolves to binder-
, MsgPassingServer (MsgPassing, serverserver.P, 10,
i2+1, synch, fifo) while i2 will be incremented. The final
effect of this rewriting (Msg-SeverGet) is necessary to
ensure synchronization of rewrites with a particular tile
(having Se
Step 2:
At this granularity level, we associate to each hierarchi-
s
Server-TS = (HServer-TS, VServer-TS, NServer-TS, RServer-TS)
C
opyright © 2010 SciRes. JSEA

A Tile Logic Based Approach for Software Architecture Description Analysis 1077
where:
OServer-TS is a set of algebraic terms defining Server class
attributes, guards and post-conditons.
HServer-TS = {BEGINServeur, S1Serveur, ENDServeur}. Objects
category correspond to tile systems associated to
r-TS = {P1: call start (), P2: call init (r: t-role, ClientID:int,
d:opaque), Perform daemon, Perform worker}. These cate-
gory objects (tile systems) are formed around actions or
transitions of the LfP-BD.
NServer-TS = {Start, Init, Daemon, Worker}
RServer-TS: N Server-TS
 H Server-TS  V Server-TS  V Server-TS 
Server-TS
tion tile: init tile (7) and one bloc-transition-tile:
worker tile (8).
of this
LfP-BD states.
VServe
H
As basic tiles example let us consider one method-
transi

Msg ServeurGet
init: BEGINClientID !=0S1
Serveur serveur
init r,ClientID,d

  (7)
Msg ServeurGetENDserveur
perform worker
worker: S1r:'worke
Serveur r '

  (8)
Tile (7) expresses evolution involved by firing action
Msg-ServerGet (tile trigger) of initial configuration
B
a h
d preserving hierarchical behaviour view,
t us consider the init-TS and the worker-TS respec-
(rÄClientIDÄd).
 Hinit-TS  Vit-TS  V H
EGINServeur composed with a new interface<ClientID ! =
0>(precondition) that is noted by BEGINserveur Ä
<ClientID ! = 0>. Effect of this tile is materialized by the
init method invocation. We notice that in a lower
abstraction level, we can define a more detailed model
through their associated hidden tile system init-TS (step 3).
The meaning of tile (8) is similar to that of tile (7).
Step 3:
For each transition method or Bloc-transition is associated
idden sub-LfP-BD, its corresponding sub-tile system is
naturally deduce
le
tively:
init-TS = (Hinit-TS, Vinit-TS, Ninit-TS, Rinit-TS)
Oinit-TS = {r, clienID, d, r1, c1, d1}
Hinit-TS = {BEGINinit, ENDinit}
Vinit-TS = {r1:= r; c1:= ClientID; d1:= d; ! (rÄClientIDÄd)}
Sequential composition of T1 actions with local context
destroy !
Ninit-TS = {T1}
Rini-TS: Ninit-TS ininit-TS init-TS


init
T1: BEGINinit r: r; c: ClientI
11


Similarly, we define
r ,C
D;
lientID,d E ND in
d )


it
d:d; !(rClientID
1

Vworker-TS = {T2 actions}
Nworker-TS = {T2}
(9)
the following detailed tile system:
w
(10)
Each one denotes and formalizes a particular architectural
description element (architecture configuration, composite
component, primitive component). Our defined modeling
process is then applied to a particular ADL, LfP allowing
modular and hierarchical description of not only software
structure, but also its behavior. Besides, LfP language
interesting and very useful to define semantics
of
riting logic but, it is even better, if the
formalism in question could be self-s
in a natural way a complete compos
to some owner theoretical and practical characteristics.
This extraordinary privilege is exactly and
by so called tile logic; a particular e
logic. This unique formal support gives good solution to
ts not
nly static and dynamic aspects of any ADL, but also
ones, such as hierarchical behaviour composi-
orker-TS = (Hworker-TS, Vworker-TS, Nworker-TS, Rworker-TS)
Oworker-TS = OServer-TS È {<r:= worker}
Hworker-TS = {BEGINworker, ENDworker} with ENDworker = S1
a Server state
T2: BEGINr'worke
worker  
6. Comments and Evaluation
The proposed Tile model for a given software architecture
description is in fact a set of hierarchical tile systems.
Rworker-TS: Nworker-TS
 Hworker-TS  Vworker-TS  Vworker-TS 
Hworker-TS
perform workerEND r'  worker
T2 actions
It is very
formalization has some limits provided by the based flat
model since it doesn’t preserve the concepts of hierarchy
and modularity [3,6,7]. Through detailed evaluation of
our approach, we highlight and summarize the important
features of our proposed tile model and that strength
rewriting model defined in [6].
extend ADL notation at a Meta level that will facilitate
formal analysis and verification.
both architectural and behavioural description in the
same formalism. This advantage has been well enough
provided by rew
ufficient to provide
itional model thanks
easily offered
xtension of rewriting
Tile logic as extension of rewriting logic suppor
o
practical
tion and synchronization. Its specific inference rules are in
C
opyright © 2010 SciRes. JSEA

A Tile Logic Based Approach for Software Architecture Description Analysis
1078
turn instantiated not freely as for rewriting logic, but in
specific context and then composed implicitly to deduce
further possible behaviours. For example, in the case of
CS-tile model, the effect (call init (r, ClientID, d)) of init
trigger of the
system init-TS. During
a computation, if init tile is executed, the system instan-
tiates T1 automatically (rewriting synchronization rule)
and then applies the horizontal tiles composition (init
l
e
orm rker), e-
hat compositional and hierarchical be-
haviour semantics are really and naturally considered
with a good rewriting synchronization; what is not so
2]. Our model also opens
nfiguration.
[1] D. Garlan and B. Schmerl,
Modelling and Analysis,” Proc
Australian Workshop on Safety Related Programmable
. 69, 2006, pp.3-17.
uccini and B. X. Li, “A Classification and
,” The f Sre, Vo
83, No. 5, May 2010, pp. 723-744.
[3] D. Regep, “LfP: un langage de spécification pour
supporter une démarche
prototypage pour les systèmes ré
oftware Architectures,”
Computer Science, Vol. 4758, 2007, pp.
tile (7), defined in Server-TS, will be the
tile T1 (9), defined in the sub tile
* T1) that involves T1 execution which creates its loca
hcontext at the beginning and destroys it at the end. In t
wo dsame way, worker tile (8) effect (perf
riggetile fined in server-TS, trs the T2 (10) defined in the
sub tile system worker-TS. Though these concrete exam-
ples, we remark t
evident in ordinary rewriting logic.
7. Conclusions
The main contribution of this paper is to propose tile logic
based modelling process of a system architectural
description preserving the modularity and the hierarchy of
initial specification, avoiding its flat form. We highlight
the interest of our approach through LfP description
language since it is equipped with rich notation allowing
modular and hierarchical specification of software
systems.
Tile logic taking into account state changes with side
effects and rewriting synchronization, has been proven as
a high level (Meta) semantic framework, more
appropriate to deal naturally with important ADL features
that are more frequent, namely their structural and
behavioural hierarchy as well as any components
composition or synchronization. This particular advan-
tage is due to the theoretical and practical characteristics
of tile logic: categorical structures, guided rewriting via
observations, flexible formats of configurations, tiles
composition through interfaces, exploitation of three
dimensional views (horizontal for structure, vertical for
behaviour evolution and the third dimension for distri-
bution).
It is obvious that defining ADL semantics within a
complete semantic framework facilitates formal executing
and analyzing of software system specification. This work
enforces and offers new possibilities for formal debugging,
checking and executing the obtained tile logic model by
mapping it into rewriting logic [18,19]. We note here that
the executable specification to be obtained consequently,
has the advantage to discard useless deductions thanks to
guided rewritings in particular. Hence, our proposed
model for LfP architecture description can provide an
executable specification in Maude system [20] and its
Université de Paris VI, 2003.
[4] R. Bruni, “Tile logic for Synchronized Rewriting of
Concurrent Systems,” PhD. Thesis, Computer Science
Department, University of Pisa, Pisa, 1999.
[5] J. Meseguer, “Conditional Rewriting Logic as a Unified
Model of Concurrency,” Journal of Theoretical
Computer Science, Vol. 96, No. 1, April 1992, pp.
73-155.
[6] C. Jerad and K. Barkaoui, “On the Use of Rewriting Logic
for Verification of Distributed Software Architecture
Description Based LfP,” 16th IEEE International
Workshop on Rapid System Prototyping (RSP'05), June
2005, pp. 202-208.
[7] C. Jerad, K. Barkaoui and G. Touzi, “A. Hierarchical
Verification in Maude of LfP S
practical checking tools [21,2
way to several other perspectives such as semantics
enrichment of LfP component behaviour under particular
constraints such dynamic reco
REFERENCES
“Architecture-Driven
eedings of the 11th
Systems (SCS’06), Vol
[2] P. Zhang, H. M
Comparison of Model Checking Software Architecture
Techniques Journal oystems and Softwal.
de développement par
partis,” thèse de doctorat,
Lecture Notes in
156-170.
[8] D. C. Lukham, “Rapide: A language Toolset for
Simulation of Distributed System by Partial Ordering of
Events,” DIMACS Workshop on Partial Order Methods
in Verification (POMIV), July 25-26, 1996, pp. 329-358.
http://pavg.stanford.edu/rapide/rapide-pubs.html
[9] R. J. Allen, “Formal Approach to Software Architecture,”
PhD. Thesis, University of Carnegie Mellon, Pittsburgh,
May 1997.
[10] C. Braga and A. Sztajnberg, “Towards a Rewriting
Semantics for a Software Architecture Description
Language,” Proceedings of the Brazilian Workshop on
Formal Methods, Vol. 95, May 2004, pp. 149-168.
[11] R. Bruni, J. Fiadeiro, I. Lanese, A. Lopes and U.
Montanari, “New Insights into the Algebraic Properties
of Architectural Connectors,” International Federation
for Information Processing, Vol. 155, 2004, pp. 367-380.
[12] R. Bruni, U. Montanari and U. Sassone, “Observational
Congruences for Dynamically Reconfigurable Tile
Systems,” Theoretical Computer Science, Vol. 335, No.
2-3, May 2005, pp. 331-372.
[13] D. Hirsch and U. Montanari, “Consistent Transformations
C
opyright © 2010 SciRes. JSEA

A Tile Logic Based Approach for Software Architecture Description Analysis
1079
op on Distributed Systems, Vol. 28, 1999.
[1
Tran-
and U. Montanari, “Mapping Tile Logic into
June
38, No. 3, June 2009, pp.
for Software Architecture Styles of Distributed Systems,”
Worksh
4] F. Arbab, R. Bruni, D. Clarke, I. Lanese and U.
Montanari, “Tiles for Reo,” Lecture Notes in Computer
Science, Vol. 5486, 2009, pp. 37-55
[15] A. Choutri, F. Belala and K. Barkaoui, “Towards a Tile
Based LfP Semantics,” Second International Conference
on Research Challenges in Information Science (RCIS
2008), June 2008, pp. 9-16.
[16] C. Bouanaka, A. Choutri and F. Belala, “On Generating
Tile System for Software Architecture: Case of a Colla-
borative Application Session,” ICSOFT’07, Barcelone,
2007, pp. 123-126.
[17] F. Gilliers, “Développement par prototypage et Génération
de Code à partir de LfP, un langage de modélisation de
haut niveau,” thèse de doctorat, Université P. & M. Curie,
Paris, 2005.
[18] R. Bruni, J. Meseguer and U. Montanari, “Tiling
sactions in Rewriting Logic,” Electronic Notes in Theore-
tical Computer Science, Vol. 71, April 2004, pp. 90-109.
[19] J. Meseguer
Rewriting Logic,” Lecture Notes in Computer Science,
Vol. 1376, 1998, pp.62-91.
[20] M. Clavel, F. Duran, E. Eker, S. N. Marti-Oliet, Lincoln,
P. J. Meseguer and C. Talcott, “Maude 2.0 Manual,”
2003. http://maude.cs.uiuc.edu
[21] S. Eker, J. Meseguer and A. Sridharanarayanan, “The
Maude LTL Model Checker and Its Implementation,”
Proceedings of the 10th International Conference on
Model Checking Software, 2003, pp. 230-234.
[22] R. Bruni, A. LIuch and U. Montanari, “Hierarchical
Design Rewriting with Maude,” Electronic Notes Theore-
tical Computer Science, Vol. 2
45-62.