 J. Software Engineering & Applications, 2010, 3, 1032-1039 doi:10.4236/jsea.2010.311121 Published Online November 2010 (http://www.SciRP.org/journal/jsea) Copyright © 2010 SciRes JISEA Challenging the Evolutionary Strategy for Synthesis of Analogue Computational Circuits Yerbol A. Sapargaliyev, Tatiana G. Kalganova Brunel University, London, UK. Email: {yerbol.sapar, Tatiana.kalganova}@brunel.ac.uk Received July 21st, 2010; revised August 27th, 2010; accepted September 2nd, 2010. ABSTRACT There are very few reports in the past on applications of Evolutionary Strategy (ES) towards the synthesis of analogue circuits. Moreover, even fewer reports are on the synthesis of computational circu its. Last fact is mainly due to the dif- ficulty in designing of the comp lex nonlinear fun ctions that these circuits perform. In this paper, the evolving power of the ES is challenged to design four computational circuits: cube root, cubing, square root and squaring functions. The synthesis succeeded due to the usage of oscillating length genotype strategy and the substructure reuse. The approach is characterized by its simplicity and represents one of the first attempts of application of ES towards the synthesis of “QR” circuits. The obtained experimental results significantly exceed the results published before in terms of the circuit quality, economy in components and computing resources utilized, revealing the great potential of the technique pro- posed to design large scale analog circuits. Keywords: Analog Circuit Synthesis, Evolutionary Electronics, Computational Circuits, SPICE 1. Introduction The Evolvable Hardware (EHW) is one of the most promising areas of today’s electronics. The EHW where the ultimate goal is an electronic circuit is also known as Evolutionary Electronics (EE) [1]. Evolutionary Algo- rithms (EA) together with a circuit simulation tool (or real hardware) automatically designs the circuit for a given problem. This approach uses very little knowledge of conventional circuit design theory and is mainly based on the exploitation of “search and test approach”. In general, EA navigated by fitness values, provides randomly created and mutated chromosomes. Each chro- mosome encodes a structure for a circuit in a form of genotype and has to be evaluated by a fitness function. The fitness function assigns each chromosome with a fitness value that defines how close the current hardware structure is to the target by its functioning. The circuits evolved may have unconventional designs and less of all depend on the personal knowledge of a designer. Nowa- days, the EA is represented by Genetic Algorithm (GA), Genetic Programming (GP) and ES. While GA is defi- nitely the most popular tool, GP is rapidly developing in recent years and is notable by its outstanding results in the area of EE. On the other hand, ES that first was in- troduced in [2], can be named as the simplest EA due to it does not use the crossover between chromosomes dur- ing mutation stage; each mutation involves only one chromosome. One of the main targets of this paper is to discover the potentials of ES in evolving large analog circuits. The second column of Table 1 carries the statis- tics on types of EAs used in other works. The analogue CCs play an important role in applica- tions where it is required to have a limited number of mathematical functions. They suggest an economy in components eliminating the analogue-digital-analogue conversion that conventional designs usually incorporate, and provide considerably shorter delay in circuit re- sponse. The vitality of CCs is well described in [3]. Today the open-ended methods of evolutionary analog circuit synthesis are questioned (i.e., in [1,4]) with an important issue, whether they are able to create solutions that are valid and trustworthy enough being realized in silicon? In [5] the set of experiments have proven that the open-ended methods enabled to design low/high-pass filters with topology-based robustness. In [6] the fre- quency discriminator robust to wide temperature range was evolved with an open-ended GA intrinsically in FPGA. The [7] describes experiments that allowed adap- tive in-situ circuit reconfiguration in extreme tempera- ture and radiation environments. In [8], the uncon- strained evolution successfully created the analog vari-  Challenging the Evolutionary Strategy to Synthesis Analogue Computational Circuits1033 ability-tolerant CMOS circuits performing XOR and XNOR functions. The literature review on that subject enables to distinguish two approaches. The first tradi- tional one follows the paradigm wherein the evolution is, firstly, set to discover the unconventional design and later the circuit is tuned to improve the robustness [6,7,9-11]. Another approach suggests for use the evolutionary sys- tem that originally purposed for the robust designs [4,5,8]. In a current work, we go along the first way focusing on exploration of technique’s capabilities to create uncon- ventional designs, leaving the evolution of robustness for the next stage experiments. The next section overviews the previous work in the area. Section 3 introduces the whole evolutionary tech- nique. Section 4 describes the experimental results to- gether with comparison with the results obtained before. And, finally, the last section concludes the paper. 2. Previous Work In the past the low-pass filters [5,10-16], high-pass filters [5,10,11,13,17,18] and amplifiers [1,9,11,12] were suc- cessfully synthesized with the help of EA. In [1] the un- constrained evolution, both spatially and temporally had been applied towards a digital reconfigurable hardware - FPGA. By releasing the full repertoire of behavior that FPGA can be manifest, namely, allowing any connec- tions among modules, letting to evolve the granularity and synchronization, evolution had been able to find a highly efficient electronic structure, which requires 1-2 orders less silicon area to achieve the same performance as conventional design does. Natural behavior of ana- logue components started to be exploited inside a digital circuit. In analogy to this approach, the unconstrained evolu- tion in our previous endeavor to sharpen our technique was applied in [16] towards the originally analogue cir- cuits (low-pass filters) and excellent results were retained. Most of the works in the area start from evolving a low-pass filter (Table 1). The last one is a convenient tool for the probation of evolutionary technique and tuning the EA parameters towards the more sophisticated designs. In this paper, we tried to evolve the computational circuits (CCs) that perform the: cube root, cubing, square root [19] and squiring functions. CCs, in contrast to filters, enable a comparison of resulted designs with circuits published before much easier. This is due to fewer numbers of characteristics that describe the circuit. A filter, besides main characteristics such as a stop-, pass- and transi- tion-bands, has the attenuation values and ripples, which are difficult to count during the comparison. In contrast, a CC is characterized only by average error of the com- puting function, which together with circuit size (com- ponent amount) and evaluation efforts gives the Table 1. Advances on the evolution of analogue circuits. Researcher EA type GLVS CSCR Koza et al. [9] GP ILG Partially Mydlowec et al. [3] GP ILG Partially Streeter et al. [20] GP ILG Partially Lohn, Colombano [11] GA ILG Yes Goh, Li [12] GA ILG Yes Zebulum, et al. [10] GP,GA ILG,OLG,UDIP Yes Grimbleby [14] GA ILG Data n/a Dastidar, et al. [21] GA OLG Yes Ando, Iba [13] GP,GA Data n/a Yes Sripramong et al. [22] GP Fixed Yes Walker et al. [8] GA Fixed Partially Chang, Hou, Su [18] GP UDIP Yes Mattiussi, Floreano [23]GA OLG Yes Gan, Yang et al. [17] CS OLG Yes McConaghy et al. [4] GP ILG Yes Kim et al. [5] ES ILG Data n/a Walker et al. [8] GP + ES OLG No Das A., Vemuri [24] GA UDIP Yes LCR Sapargaliy- ev et al. [16] OLG ES No QR(current)OLG ES No CSCR is for circuit-structure-checking rules; PO is for parameter optimiza- tion; GLVS is for the genotype length varying strategies; CS is for Clonal Selection. sufficient picture to judge on capabilities of the method- ology. Works [10,13] gave the comparison between GP and GA. The first work was made as an analogy to the biology concept with comparison of different types of variable length genotypes strategies, whereas in the second one it was intrinsic evolution of a real hardware for robustness purposes. According to [10], the “genotype length varying strategies” refer to the way in which the chromosome’s lengths are sampled by the EA at each generation. It is easy to follow this idea if one looks at sizes of the best circuits throughout the generations. There were different kinds of strategies introduced in [10], where two of them have shown excellent results: Increasing Length Geno- types (ILG) and Oscillating Length Genotypes (OLG). If it occurred that the size of the best circuit at each fol- lowing generation never decrease than it is ILG, otherwise it is OLG. The OLG strategy is a kind of ILG in which the genotypes are also allowed to decrease in size. The main purpose of OLG is to create pathways from large to smaller genotypes with improved fitness values. The third column of Table 1 summarizes the information on OLG vs. ILG. Most of the works focus on such circuits like filters and amplifiers which, we think, are not an adequate enough challenge for the probation of the up-to-date evolutionary Copyright © 2010 SciRes JILSA  Challenging the Evolutionary Strategy to Synthesis Analogue Computational Circuits 1034 techniques. Current research is devoted to CCs which are the ones of most provoking issues for any automatic cir- cuit synthesis system. It should be mentioned that the largest analog circuit evolved in the area of EE is a squire root circuit with 64 components in [9]. We found another three papers on CCs [3,24,25] that regarded the same circuits as in this paper. In [3,9,20] they used GP cir- cuit-constructing program trees approach with four kinds of functions. They also used automatically defined func- tions and potentially enabled certain substructures to be reused. The paper [9] suggests an attractive opportunity among all others for judging on effectiveness of the evo- lutionary tool. Targeting to the same arithmetic functions and utilizing an identical evaluation procedure (fitness function), one can directly compare the fitness values (average error), circuit size (economy) and PC time spent. In this paper, we took advantage of this opportunity. In [3] two CCs were developed by the similar evolu- tionary technique as in [9], however they used time-con- tinues signals in time-domain simulations. The transient analysis of a circuit in contrast to DC-analysis provided more robust circuits despite the higher time-consumption to complete the analysis. The patent in [25] presents the conventionally designed cubing CC, that was improved in [19] by iterative refinement method. Both are taken for comparison in Section 4. The work in this paper contributes to the following is- sues of EE: a) discovers the potentials of ES towards the design of nonlinear analog circuits, and b) reveals the ability of unconstrained evolution to find more efficient and unconventional designs. 3. Evolutionary Technique of QR Circuits Reaching successful circuits most of all depends on an evolutionary technique that worked out and applied. The last one is a set of rules according to which, parameters of EA (e.g., mutation rate, crossover, selection, etc.), geno- type length varying strategies [10], mutation types and the circuit representation technique are managed. 3.1. Encoding (Representation) We use only three types of components as in [3,9]: Qn – the n-p-n bipolar transistor, Qp – the p-n-p bipolar tran- sistor and R – resistor. The linear circuit representation proposed for use, i.e., every component of a circuit rep- resented as a particular gene, and each gene consisted Rx N1 N2 Pa Qx N1 N2 N3 (a) (b) Figure 1. A gene coding (a) resistor; (b) bipolar transistor. Rx-loci and Pa-loci are the resistor’s name and parameter; Qx-loci is the transistor’s name; N1, N2, N3-loci are the nodes for the first, the se c o nd and the thir d pins. of 4 loci corresponding to component’s features: name, node numbers to each pin and parameter (only for R). On Figure 1 is a view of a gene coding a resistor (a) and a bipolar transistor (b). The gene looks exactly the same as a component line in the PSPICE netlist, so, there is no necessity to convert a genotype into a netlist. The sim- plicity of linear representation we utilized simplifies the terminology, for example, we mean “a circuit” when we mention “a chromosome”, we mean “a component” when we mention “a gene”, we mean “a population” when we mention “a netlist”, and vice versa. For a resistor’s Pa-loci, we set 64 possible values of E-12 series, i.e., there were 5 decades from 10 Ω to 1E + 6 Ω available for evolution, plus four additional parameters. 3.2. Unconstrained Evolution of “QR” Circuit In an analogue domain, the circuit-structure-checking rules at the netlist composition stage that prohibit some circuits to be tested/simulated were regarded as the main constraints in evolution. The target of these rules is usu- ally increasing the portion of rightly analyzed circuits as well as the avoiding time consumptions during resolving the implausible designs by simulation software. In [16] we called “absolutely unconstrained evolution of an analogue circuit” the process of circuit netlist generation during which no circuit-structure-checking rules applied and all the circuits are counted as valid graphs except ones that have components with dangling nodes and with isolated sub-circuits. We utilized special technique that enabled us to avoid most of the errors inherent to circuits built up of reactive components inductors and capacitors. In a current work we use Qn, Qp and R components. Here transistors can lead to unconvergences during anal- ysis. Therefore, in most of the works in Table 1 (column 4) the rules banning some transistor connections, such like emitter-to-collector and base-to-PS, were applied. In this paper, we did not apply any prohibitions to any kind of connections. We also did not prohibit the formation of “loops” of components during circuit growth. “Loop” (or sub-circuit) is a component or a group of components aside from the main circuit that does not connect to the main circuit or connects to it only via alone node. “Loops” mainly do not influence on functionality of the whole circuit, however, they participate in carrying the neutral mutations [1]. The statistics on constraint/un- constraint methods in the area of analog EE are shown in the fourth column of Table 1. The transient analysis applied to perform the evalua- tion instead of DC-analysis. Due to the tolerance that transient analysis expresses to the same circuits that under the DC-analysis are treated as unconvergent [26], we could maximize the portion of valid chromosomes in each population. This hint allows the multitude of indi- Copyright © 2010 SciRes JILSA 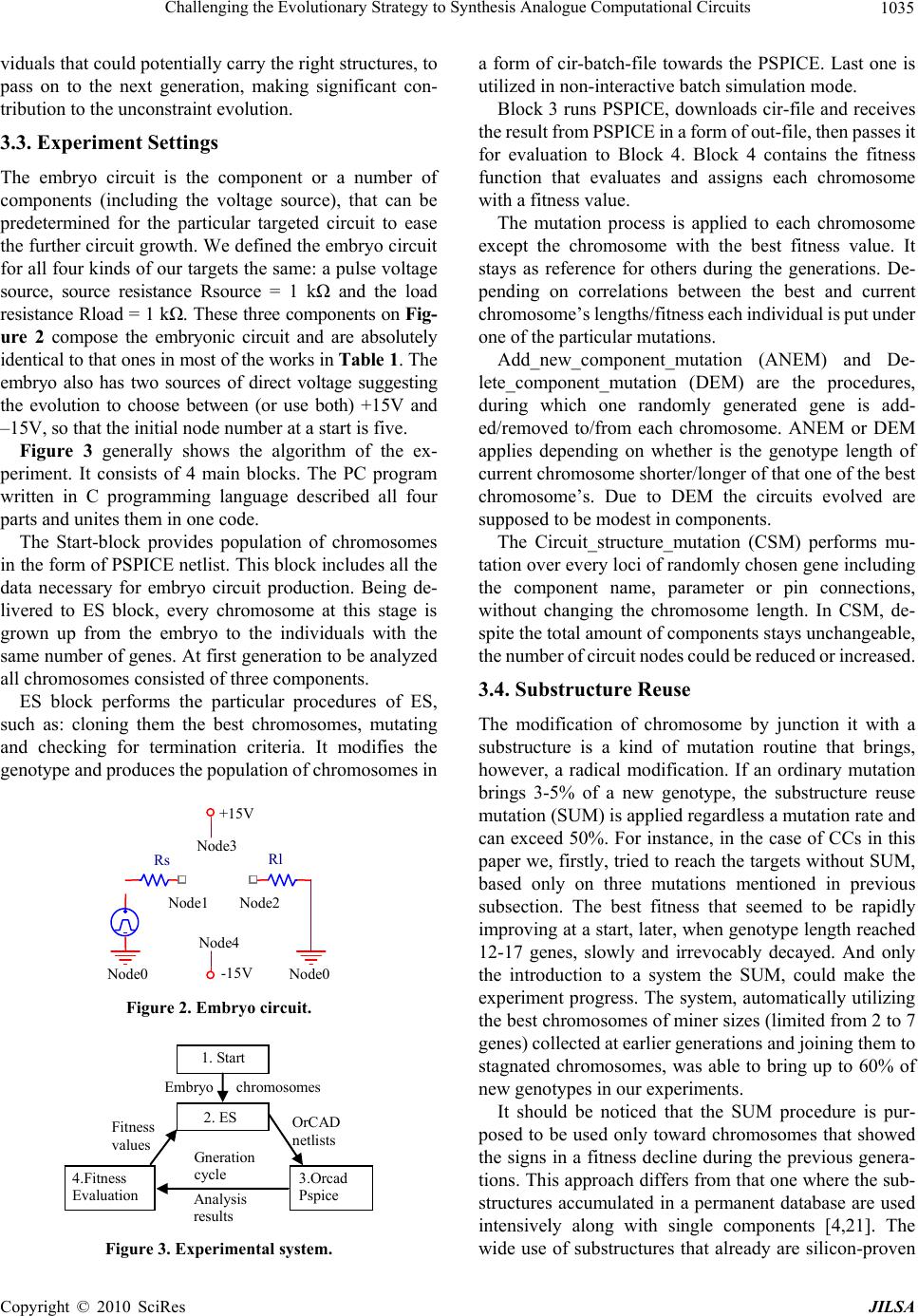 Challenging the Evolutionary Strategy to Synthesis Analogue Computational Circuits1035 viduals that could potentially carry the right structures, to pass on to the next generation, making significant con- tribution to the unconstraint evolution. 3.3. Experiment Settings The embryo circuit is the component or a number of components (including the voltage source), that can be predetermined for the particular targeted circuit to ease the further circuit growth. We defined the embryo circuit for all four kinds of our targets the same: a pulse voltage source, source resistance Rsource = 1 kΩ and the load resistance Rload = 1 kΩ. These three components on Fig- ure 2 compose the embryonic circuit and are absolutely identical to that ones in most of the works in Table 1. The embryo also has two sources of direct voltage suggesting the evolution to choose between (or use both) +15V and –15V, so that the initial node number at a start is five. Figure 3 generally shows the algorithm of the ex- periment. It consists of 4 main blocks. The PC program written in C programming language described all four parts and unites them in one code. The Start-block provides population of chromosomes in the form of PSPICE netlist. This block includes all the data necessary for embryo circuit production. Being de- livered to ES block, every chromosome at this stage is grown up from the embryo to the individuals with the same number of genes. At first generation to be analyzed all chromosomes consisted of three components. ES block performs the particular procedures of ES, such as: cloning them the best chromosomes, mutating and checking for termination criteria. It modifies the genotype and produces the population of chromosomes in -15V Rs Rl ode0 ode2 ode3 ode1 ode4 ode0 +15V Figure 2. Embryo circuit. Fitness values OrCAD netlists Gneration cycle 2. ES Analysis results 4.Fitness Evaluation 3.Orcad Pspice 1. Start Embryo chromosomes Figure 3. Experimental system. a form of cir-batch-file towards the PSPICE. Last one is utilized in non-interactive batch simulation mode. Block 3 runs PSPICE, downloads cir-file and receives the result from PSPICE in a form of out-file, then passes it for evaluation to Block 4. Block 4 contains the fitness function that evaluates and assigns each chromosome with a fitness value. The mutation process is applied to each chromosome except the chromosome with the best fitness value. It stays as reference for others during the generations. De- pending on correlations between the best and current chromosome’s lengths/fitness each individual is put under one of the particular mutations. Add_new_component_mutation (ANEM) and De- lete_component_mutation (DEM) are the procedures, during which one randomly generated gene is add- ed/removed to/from each chromosome. ANEM or DEM applies depending on whether is the genotype length of current chromosome shorter/longer of that one of the best chromosome’s. Due to DEM the circuits evolved are supposed to be modest in components. The Circuit_structure_mutation (CSM) performs mu- tation over every loci of randomly chosen gene including the component name, parameter or pin connections, without changing the chromosome length. In CSM, de- spite the total amount of components stays unchangeable, the number of circuit nodes could be reduced or increased. 3.4. Substructure Reuse The modification of chromosome by junction it with a substructure is a kind of mutation routine that brings, however, a radical modification. If an ordinary mutation brings 3-5% of a new genotype, the substructure reuse mutation (SUM) is applied regardless a mutation rate and can exceed 50%. For instance, in the case of CCs in this paper we, firstly, tried to reach the targets without SUM, based only on three mutations mentioned in previous subsection. The best fitness that seemed to be rapidly improving at a start, later, when genotype length reached 12-17 genes, slowly and irrevocably decayed. And only the introduction to a system the SUM, could make the experiment progress. The system, automatically utilizing the best chromosomes of miner sizes (limited from 2 to 7 genes) collected at earlier generations and joining them to stagnated chromosomes, was able to bring up to 60% of new genotypes in our experiments. It should be noticed that the SUM procedure is pur- posed to be used only toward chromosomes that showed the signs in a fitness decline during the previous genera- tions. This approach differs from that one where the sub- structures accumulated in a permanent database are used intensively along with single components [4,21]. The wide use of substructures that already are silicon-proven Copyright © 2010 SciRes JILSA  Challenging the Evolutionary Strategy to Synthesis Analogue Computational Circuits Copyright © 2010 SciRes JILSA 1036 could fasten the road of evolved designs to a commercial application, but in the scope of this paper, as mentioned in Section 1, we focus first on the exploring power of the evolutionary system. Table 2. Statistics for evolution of the 4 targeted circuits. Fitness Com- ponent No Gen- eration No Fitness Compo- nent No Gen- eration No No Square Root Squaring 10.28343 119 0.0302 35 92 20.19423 123 0.0459 43 309 30.44350 208 0.0563 48 143 40.79838 97 0.0951 38 97 50.25550 200 0.0776 50 135 Cube Root Cubing 10.76444 115 0.0095 50 195 21.06049 179 0.0205 38 72 30.25139 152 0.0079 49 109 40.26850 201 0.0061 44 78 50.64340 294 0.0101 37 98 Altogether ANEM-CSM-DEM-SUM enables to hold a population within restrained chromosome’s lengths and for evolution to be more focused. In general, each chro- mosome in a population is allowed gradually grow, where the speed of growth is controllable with the help of an automatic/manual tunable threshold coefficient. 3.5. Fitness Function The target for evolutionary search is to evolve four CCs which output voltages are: the cube root, cube, square root and square of their input voltages. To enable our- selves to make the estimation of the final results, we have set the same fitness terms as in [9] for all four cases. That are, we made the PSPICE simulator to perform a transient analysis of a source signal of length 0.2 second at 21 equidistant time-points; the voltage source forms a pulse signal arising from –250 mV to +250 mV for the cube root, cubing and squaring, and from 0 mV to +500 mV for the square root [19]. A fitness value is set to the sum, over these 21 fitness cases of the absolute weighted deviation between the target value and the actual output Qp 2 -15V -15V Qp 2 7 Qp 2 3 15V 15V Qn13 Qp25 R31 1e+4 Qn1 R37 3.3e+6 V_IN Rs 1K V_OUT Rl1K Qn 1 5 R1 1.5e+4 R0 1.2e+4 R4 1.5e+6 R5 4.7e+3 Qp5 Qn 3 -15V R13 1.34e+6 -15V R364.3e+4 R6 5.6e+3 15V R2 2.2e+4 Qp24 Qp10 Qp20 value: , where is the voltage p i i measured i ideal VVF 0 || i ideal VFigure 4. The evolved square root circuit. in i-th point for the ideal response and is the voltagein the i-th point obtained for the evolved circuit; p is a number of points evaluated equaling 21. The smaller the fitness value, the closer the circuit is to the target; the fitness penalizes the output voltage by 10 if it is not within 1% of the target voltage value. i measured V R0 2.7e+4 Qp4 0 Qp 3 15V Qp38 Qp2 0R42 6e+4Qp3 0 R21 2.27e+5 Qp10 Qp3 5 Qp3 3 Qp16 15V Qp1 2 V_IN Rs 1K Qp1 R7 820 V_OUT Rl 1K Qp4 4 Qn1 7 Qn2 8 Qn4 1 Qn 1 Qn14 15V R2 1.815e+1 Qn2 Qp0 R39 4.73e+6 Qn40 -15V Qp39 Qp2 4 Qp 7 Qp21 Qp43 Qn3 5 Qn1 0 Qn7 15V R10 2.82e+4 The circuits that were treated by PSPICE as error car- rying were assigned to the worst fitness. We set as a ter- mination criterion reaching either the fitness value did not improve over 20 consecutive generations or the best cir- cuit exceeded 70 components in size. 4. Experimental Results The results presented are out of 5 runs for each case with different seeds for the random number generator. The aggregated data for all 20 runs are presented in Table 2, where the best runs are marked in bold. We used 10 PCs with Pentium-4/2.8 GHz processor running at the same time independently from each other. The average time per experiment is 43 hours. The total population was 30000 individuals, mutation rate 5% and selection 10%. Figure 5. The evolved squaring circuit. ponents with the fitness 0.0302. The best-of-run circuit (Figure 6) for the problem of designing a cube root circuit appeared at generation 152 and had 39 components with the fitness 0.2508. The best-of-run circuit (Figure 7) for the problem of design- ing a cubing circuit appeared at generation 78 and has 44 components with the fitness 0.00614. The best-of-run circuit (Figure 4) for the problem of designing a square root circuit has 23 components with the fitness 0.194. The best-of-run circuit (Figure 5) for the problem of designing a squiring circuit has 35 com- 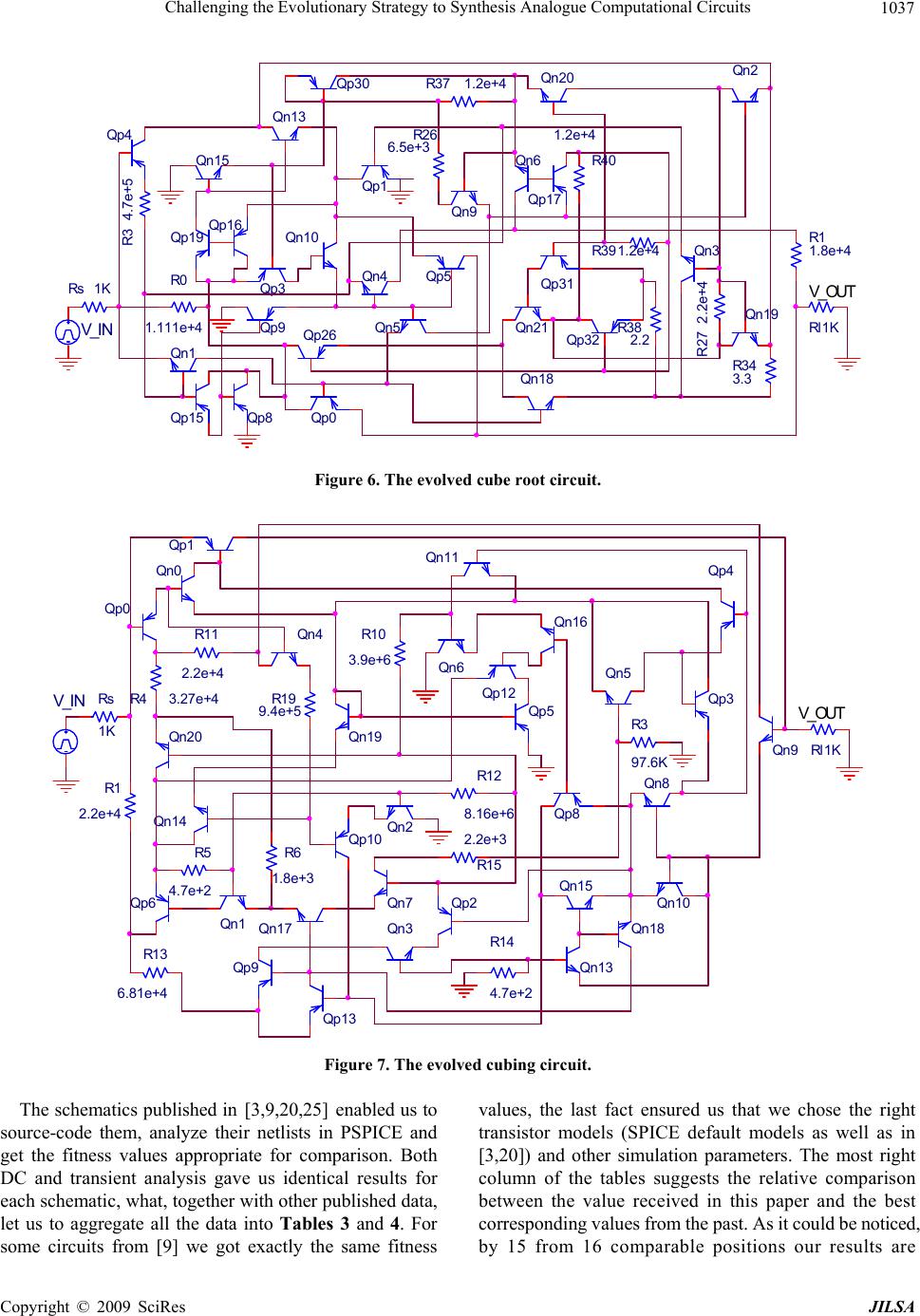 Challenging the Evolutionary Strategy to Synthesis Analogue Computational Circuits1037 V_OUT Rl1K Qp 3 Qn10 Qp15 Qn 3 Qn 6 Qp17 R37 1.2e+4 Qp 16 Qp 9 Qp19 Qp26 R40 1.2e+4 R26 6.5e+3 Qn 9 Qn2 Qp 5 Qn5 Qn21 Qp8 Qn4 Qp32 R272.2e+4 Qp31 R3 4.7e+5 Qp1 Qn13 Qp 0 R1 1.8e+4 R391. 2e+4 R34 3.3 Qn19 Qn 15 Rs 1K V_IN Qp4 R0 1.111e+4 Qn 1 Qp30 Qn20 R38 2.2 Qn18 Figure 6. The evolved cube root circuit. Rs 1K V_IN Qp 0 Qn 0 Qn7 R1 2.2e+4 Qn20 Qn6 Qn 5 Qp12 Qn2 Qp 10 Qp9 Qp13 Qn1 R5 4.7e+2 R6 1.8e+3 Qn17 R12 8.16e+6 Qp6 R13 6.81e+4 Qp5 R3 97.6K Qn16 Qp8 Qp4 Qp1 Qn3 Qp 2 Rl1K V_OUT Qn1 3 Qn9 R10 3.9e+6 Qn 19 Qn1 8 Qn14 R43.27e+4 Qn 15 R11 2.2e+4 R19 9.4e+5 Qn 8 Qn10 R14 4.7e+2 R15 2.2e+3 Qn4 Qn11 Qp3 Figure 7. The evolved cubing circuit. The schematics published in [3,9,20,25] enabled us to source-code them, analyze their netlists in PSPICE and get the fitness values appropriate for comparison. Both DC and transient analysis gave us identical results for each schematic, what, together with other published data, let us to aggregate all the data into Tables 3 and 4. For some circuits from [9] we got exactly the same fitness values, the last fact ensured us that we chose the right transistor models (SPICE default models as well as in [3,20]) and other simulation parameters. The most right column of the tables suggests the relative comparison between the value received in this paper and the best corresponding values from the past. As it could be noticed, by 15 from 16 comparable positions our results are Copyright © 2009 SciRes JILSA  Challenging the Evolutionary Strategy to Synthesis Analogue Computational Circuits 1038 Table 3. Comparison with circuits published before. Author Feature Koza et al. [9] Mydlowec et al. [3] This work Improve- ment (times) Square root Average error, mV 183.57 20.00 9.23 2.2 Fitness value 3.855 70.403 0.194 18.9 Component No 64 39 22 1.8 Evaluation No Data n/a 6,7E + 9 3,7E + 6 1800 Squiring Average error, mV Data n/a 27.00 1.44 18.7 Fitness value Not converged 4.812 0.0302 159.3 Component No 39 37 35 1.1 Evaluation No Data n/a 1,1E + 9 2,7E + 6 407 Cube root Average error, mV 80.00 - 11.90 6.7 Fitness value 1.68 - 0.2508 6.7 Component No 50 - 39 1.3 Evaluation No 3.8E + 7 - 4.5E + 6 8.4 Table 4. Comparison of evolved cubing circuit with ones published previously. Author Feature Koza et al.[9] Streeter et al.[19] Cipriani et al. [25] This work Improve- ment (times) Cubing Aver.error, mV 1.04 0.99 7.13 0.29 3.4 Fitness value 0.0219 Data n/aData n/a 0.0061 3.6 Component No 56 47 12 44 0.3 Evaluation No Data n/a 2.94E + 6- 2.34E + 61.3 considerably better. Notably, that the best by size (12 components) conventionally designed cubing circuit from [25] has an average error (7.13 mV) 25 times larger than that one (0.29 mV) of cubing circuit (44 components) evolved by us. 5. Conclusions In this paper, we applied the unconstrained evolution towards the design of analogue computational circuits, on the example of cube root, cubing, square root and squiring functions. It was one of the first successful attempts of application of Evolutionary Strategy (ES) towards the large analog circuit synthesis. The technique presented is based on ES, oscillating length genotype, three types of mutation and substructure reuse. In general, the technique is plain with a simple algorithm. In all four cases, we successfully evolved circuits with fewer numbers of components at much less computer efforts with signifi- cantly better fitness. The work discovered the capabilities of the technique developed by authors to find unconventional, economic and precise solutions. However, the designs presented are just simulated models, and are not guaranteed to be robust being in silicon. There are still “countervailing factors that impede progress toward industrial-strength automated design of analog circuits” [27] such as mismatching properties of devices, variation in the circuit’s power supply and different operating temperatures. Reaching the powerful evolutionary technique that capable of finding theoretical solutions was only the first stage of the research, whereas the second round is pur- posed to be strengthening the designs evolved towards the robust circuits in silicon. REFERENCES [1] A. Thompson, “Artificial Evolution in the Physical World,” In: Gomi, Ed., Evolutionary Robotics, AAI Books, 1997, pp. 101-125. [2] R. Ingo, “Optimierung Technischer Systeme Nach Prin- zipien der Biologischen Evolution,” PhD Dissertation, Technical University of Berlin, 1970. [3] W. Mydlowec and J. Koza, “Use of Time-Domain Simu- lations in Automatic Synthesis of Computational Circuits Using Genetic Programming,” Genetic and Evolutionary Computation Conference, Las Vegas, 2000, pp. 187-197. [4] T. McConaghy and G. G. E. Gielen, “Globally Reliable Variation-Aware Sizing of Analog Integrated Circuits via ResponseSurfaces and Structural Homotopy,” IEEE Transactions on Computer-Aided Design, Vol. 28, No. 11, November 2009, pp.1627-1640. [5] K. Kim, A. Wong and H. Lipson, “Automated Synthesis of Resilient and Tamper-Evident Analog Circuits without a Single Point of Failure,” Genetic Programming and Ev- olvable Machines (online), 2009. [6] A. Thompson and P. Layzell, “Evolution of Robustness in an Electronics Design,” International Conference on Intelligent Engineering Systems, Springer, 2000, pp. 218-228. [7] A. Stoica, D. Keymeulen, T. Arslan, V. Duong, R. Zebu- lum, I. Ferguson and X. Guo, “Circuit Self-Recovery Experiments in Extreme Environments,” Proceedings of the 2004 NASA/DoD Conference on Evolvable Hardware, Seattle, June 2004, pp. 142-145 [8] J. Walker, J. Hilder and A. Tyrrell, “Towards Evolving Industry-Feasible Intrinsic Variability Tolerant CMOS Designs,” 11th IEEE Congress on Evolutionary Compu- tation, Trondheim, May 2009, pp. 1591-1598. [9] J. Koza, “Automated Synthesis of Computational Circuits Using Genetic Programming,” IEEE Conference on Evo- lutionary Computation, Piscataway, 1997, pp. 447-452. [10] R. Zebulum, M. Pacheco and M. Vellasco, “Comparison of Different Evolutionary Methodologies Applied to Electronic Filter Design,” IEEE Conference on Evolu- tionary Computation, Piscataway, 1998, pp. 434-439. [11] J. Lohn and S. Colombano, “Automated Analog Circuit Synthesis Using a Linear Representation,” The 2nd In- ternational Conference on Evolvable Systems: From Bi- Copyright © 2010 SciRes JILSA  Challenging the Evolutionary Strategy to Synthesis Analogue Computational Circuits Copyright © 2010 SciRes JILSA 1039 ology to Hardware, Springer-Verlag, 1998, pp. 125-133. [12] C. Goh and Y. Li, “GA Automated Design and Synthesis of Analog Circuits with Practical Constraints,” Proceed- ings of the 2001 Congress on Evolutionary Computation, Vol. 1, 2001, pp. 170-177. [13] S. Ando and H. Iba, “Analog Circuit Design with a Vari- able Length Chromosome,” Proceedings of the 2000 Congress on Evolutionary Computation, Vol. 2, 2000, pp. 994-1001. [14] J. Grimbleby, “Hybrid Genetic Algorithms for Analogue Network Synthesis,” Proceedings of the 1999 Congress on Evolutionary Computation, 1999, pp. 1781-1787. [15] J. Hu, X. Zhong and E. Goodman, “Open-ended Robust Design of Analog Filters Using Genetic Programming,” Genetic & Evolutionary Computation Conference, Vol. 2, 2005, pp. 1619-1626. [16] Y. Sapargaliyev and T. Kalganova, “On Comparison of Constrained and Unconstrained Evolutions in Analogue Electronics on the Example of LC Low-Pass Filters,” IEICE Transactions on Electronics, Vol. E89-C, No. 12, December 2006, pp. 1920-1927. [17] Z. Gan, Z. Yang, G. Li and M. Jiang, “Automatic Syn- thesis of Practical Passive Filters Using Clonal Selection Principle-Based Gene Expression Programming,” Pro- ceedings of the 7th International Conference on Evolv- able Systems: From Biology to Hardware (ICES'07), Vol. 4684, 2007, pp. 1611-3349. [18] S. Chang, H. Hou and Y. Su, “Automated Passive Filter Synthesis Using a Novel Tree Representation and Ge- netic Programming,” IEEE Transactions on Evolutionary Computation, Vol. 10, No. 1, February 2006, pp. 93-100. [19] D. Smith, “A Square Root Circuit to Linearize Feedback in Temperature Controllers,” Journal of Physics E: Sci- entific Instruments, Vol. 5, No. 6, 1972, pp. 528-529. [20] M. Streeter, M. Keane and J. Koza, “Iterative Refinement of Computational Circuits Using Genetic Programming,” Proceeding of the 2002 Genetic and Evolutionary Com- putation Conference, 2002, pp 877-884. [21] T. Dastidar, P. Chakrabarti and P. Ray, “A synthesis Sys- tem for Analog Circuits Based on Evolutionary Search and Topological Reuse,” IEEE Transactions on Evolu- tionary Computation, Vol. 9, No. 2, 2005, pp. 211-224. [22] T. Sripramong and C. Toumazou, “The Invention of CMOS Amplifiers Using Genetic Programming and Cur- rent-Flow Analysis,” IEEE Transactions on Com- puter-Aided Design of Integrated Circuits and Systems, Vol. 21, No. 11, 2002, pp.1237-1252. [23] C. Mattiussi and D. Floreano, “Analog Genetic Encoding for the Evolution of Circuits and Networks,” IEEE Tran- sactions on Evolutionary Computation, Vol. 11, No. 5, 2007, pp. 596-607. [24] A. Das and R. Vemuri, “An Automated Passive Analog Circuit Synthesis Framework using Genetic Algorithms,” Proceedings of the IEEE Computer Society Annual Sym- posium on VLSI, 2007, pp. 145-152. [25] S. Cipriani and A. Takeshian, “Compact Cubic Function Generator,” U. S. Patent 6,160,427, Filed 4 September 1998, Issued December 12, 2000. [26] OrCAD, Inc. “OrCad PSpice User’s Guide,” OrCAD, USA, 2004. http://www.electronics-lab.com/downloads/ schematic/013/tutorial/PSPCREF.pdf [27] J. Koza, L. Jones, M. Keane, M. Streeter and S. Al-Sakran, “Toward Automated Design of Indus- trial-Strength Analog Circuits by Means of Genetic Pro- gramming,” Genetic Programming Theory and Practice II, Kluwer Academic Publishers, Boston, 2004.
|