 Journal of Mathematical Finance, 2013, 3, 329-334 http://dx.doi.org/10.4236/jmf.2013.32033 Published Online May 2013 (http://www.scirp.org/journal/jmf) An Empirical Study of Option Prices under the Hybrid Brownian Motion Model Hideki Iwaki1, Lei Luo2 1Faculty of Business Administration, Kyoto Sangyo University, Kyoto, Japan 2Finance Division, Citigroup Global Markets Japan, Tokyo, Japan Email: iwaki@cc.kyoto-su.ac.jp, lei.luo@citi.com Received February 20, 2013; revised April 3, 2013; accepted April 21, 2013 Copyright © 2013 Hideki Iwaki, Lei Luo. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT In this paper, we mainly discuss an empirical study of option prices under the hybrid Brownian motion model devel- oped by [1]. In a specific case of parameters, we have a simple transition probability density function that has a fat- tailed feature as time passes. We show some empirical evidences that the feature of the model reflects the real market price movements in Japanese stock market. Furthermore, we make a performance comparison between the hybrid model and the BS model using Nikkei 225 call options. In general our results show that the hybrid model is slightly better than the BS model. Keywords: Hybrid Brownian Motions; Fat-Tailed Properties; Non-Normal Distribution; Empirical Studies; Nikkei 225 Index Options 1. Introduction Measuring the risk of financial assets and pricing the financial instruments such as options are very important for financial institutions and other companies. In this area, the normal distribution is commonly used as a distribu- tion of stock return and the Black-Scholes (BS) model based on the normal distribution is mostly used in prac- tice. But fat-tailed and non-normal distributions of stock return are shown by plenty of empirical evidences. As early as 60s, [2,3] suggested the use of heavy tailed dis- tributions to describe daily returns. Reference [4] com- pared the stable distribution and t-distribution for stock prices of United States. Reference [5] presented an em- pirical evidence of the normal inverse Gaussian dis- tribution and t-distribution in the European market. As to Japanese market, [6] extensively studied on a Pearson type distribution and made an empirical study in Japa- nese stock market. The financial crisis of 2007-2009 made it clear that the extreme movements of stock return were much more likely than normal distribution. After the financial crisis the world financial market has become more and more turbulent. European sovereign debt crisis is getting worse and the governors of EU are trying to solve the problem. The companies in Japan also suffered the loss from af- termath of the earthquake in northern Japan in March 2011. Based on the facts mentioned above, we need a new approach which reflects the fat-tailed property to evalu- ate financial assets and instruments. In the paper, we in- vestigate validity of a stochastic differential equation (SDE) that is a hybrid of arithmetic and geometric Brownian motion introduced by [1]. They made an analysis on a model of the market that involves two types of market participants such as fundamental traders and technical traders. Through the analysis they pointed out that the log-return approximately follows such a hybrid Brownian motion. When we specify some parameter values, we can ex- plicitly derive a transition probability density and the variance of its distribution is increasing exponentially as time passes. This special case might reflect the real mar- ket movements in short term especially in some situa- tions like financial crises. We have fitted the model to the Japanese stock market. We show the distribution can describe the market well compared with normal distribu- tion if we focus on the short term or daily. A well-known empirical bias associated with the BS model is the volatility smile which is shown by [7] etc. The volatility is assumed to be constant in the BS model, but realized volatility of underlyings actually rise and fall C opyright © 2013 SciRes. JMF  H. IWAKI, L. LUO 330 over time. Corresponding to the observed volatility fluc- tuation, [8] introduced a stochastic volatility model and [9] gave a closed-form solution for option pricing under the stochastic volatility model. Reference [10] has made a thorough empirical study about the performance of the stochastic volatility model. When volatility is merely a function of the current asset level and time, we have a local volatility model which is a useful simplification of the stochastic volatility model. The local volatility model is developed by [11]. The hybrid model is a kind of local volatility models. To show the performance of the hybrid model in op- tion pricing empirically, we compare the performance between the hybrid model and the BS model using Nik- kei 225 index options. Since we cannot get a closed-form option pricing formula under the hybrid model, we im- plement the risk neutral option pricing by applying a tri- nomial tree method. We compare two models in an in- sample parameter estimation and an out-of-sample pric- ing performance. Our empirical evidence indicates that generally the hybrid model is slightly better than the BS model. The rest of the paper is organized as follows. Section 2 introduces the hybrid Brownian motion model and its special case. We can use this special case to describe the turbulent financial environments. Section 3 discusses fat- tailed property of the model. If we focus on distributions of daily returns, we can find that the model can fit the market data well. Section 4 shows the results of our em- pirical studies on comparison of option pricing under the hybrid model with that under the BS model and discusses some performance issues. Section 5 is our conclusion. 2. The Hybrid Brownian Motion 2.1. A General Model We consider a market containing a stock with share price at time . The log-return tt S0t is given by 0 log tt SS. Reference [1] introduced a hybrid SDE mixing both arithmetic and geometric Brownian motions to describe fluctuation of t . They make a model of market with two different types of agents. One set of agents consists of fundamental traders acting independ- ently of the current value of t . The other set consists of technical traders that trade based on the historical val- ues |0 s st. They show that after some appro- priate linearization and approximation, the aggregation of those two type trader's impacts on the log-return of stock prices leads to a general form of the hybrid SDE; 1211 22 ddd tttt d, t Xt WXW (1) where 1 , 2 , 1 and 2 are constants, and where 1t and 2t W are standard Brownian motions. In Equa- tion (1), the part of the arithmetic Brownian motion is related to the fundamental trades. On the other, the part of the geometric Brownian motion is related to the tech- nical trades. We can of course reduce it to an SDE with a single noise term. If W is the infinitesimal correlation coefficient between the two Brownian motions, then we can rewrite the SDE as 222 2 12121 2 dd 2 d tt ttt .XtXX W (2) The model has five parameters 1 , 2 , 1 , 2 and . W can explain them intuitively. 1 e is t funda- mental volatility related to the economy. 2 he is t in- vestor volatility related to the market confidence of in- vestors. 1 he is the drift related to the economy itself. 2 is the drift controlled by the investor sentiment. represes the relationship between the two volatilities above. nt 2.2. A Special Case Although there might be some positive or negative rela- tionship between 1 W and 2 W, investors cannot get the accurate information about the relationship because of information asymmetry in the financial market. They might just react randomly to the price of stock. So it might be reasonable to assume 0 . 1 also has mi- nor influence to analyze the model especially for a short term. Thus we adopt such a special case that 10 . Under the special case, [1] show the variance t VX can be written in such a tractable form that 2 2 2 1 1 2 2 2 2 2 22 2 23 112 1e ~2, t t VX ttOt where 2 2 2 2 1. plays an essential dynamic role. Assuming the condi- tion 0 , we can find that the variance grows expo- nentially as time passes. It makes fatten the tails of dis- tribution of t . Under the assumption that 0 we can simplify Equation (2) as 2 222 2 12 dd tt d 2tt .XtX W (3) We observe the momentum property from Equation (3). Since 2 in the general model is substituted by 2 22 , the positive (negative) return will try to bring a positive (negative) return next day. This mean-reversion condition in turn allows an equilibrium to establish. In general, the transition probability density of t is an integral of a hyper-geometric function of complex pa- rameters. However [1] show that under this special case Copyright © 2013 SciRes. JMF  H. IWAKI, L. LUO 331 with 0 , the transition probability density , xt of t is explicitly given by 222 12 2 21 221 1 ,fxt 2π 1 exp sinh. 2 tx tx (4) We note that we do not have any closed form transi- tion probability density except for this special case. 3. An Evidence of a Fat-Tailed and Non-Normal Distribution We show evidence such that logarithmic returns of Nik- kei 225 index follow a fat-tailed and non-normal distri- bution. We use daily closing prices of Nikkei 225 index from January 04, 2008 to September 30, 2011 which corresponds to 915 observations. Figure 1 shows normal QQ-plots for the corresponding logarithmic returns. For the Nikkei 225 index distribution, both tails are heavier than the Gaussian. Since our main interest is in the tails of the distribu- tions, we use graphical logarithmic left and right tail tests employed by [5] to examine the fit in the tails. The graphical tests were performed as follows. Let x denote the estimated cumulative distribution function of the fitted distribution, computed by numerical integration of Equation (4), and 1,, X log the order statistic of the historical data. A plot of t X against t superimposed onto a plot of g 11N lo against t shows the left tail fit for the fitted distribution, and a plot of against t FX log 1t superimposed onto a plot of log 1Nt 1N, the right tail fit. Figure 1. QQ-plots for log returns of Nikkei 225 index. Figure 2 shows the plots. The upper panel in the fig- ure shows the left tail fit, and the lower panel the right tail fit. The circles correspond to the empirical data, the line plotted around the circles corresponds to the distri- bution Equation (4), and the line deviating from the cir- cles corresponds to the normal distribution. We can find the distribution Equation (4) fits the index daily return quite well. 4. Option Pricing and Empirical Tests 4.1. An Numerical Approach for Option Pricing As we discussed in the previous sections, the hybrid model has some good features to describe the financial market. In some situations the pricing of options based on this model might be better than the traditional pricing based on the BS model. Since we cannot find a closed form option pricing formula under the hybrid model, we use a trinomial tree pricing method to derive the prices of European call options. We assume that there exists a constant instantaneous risk-free rate and there does not exist any arbitrage opportunities. Let us define r e, 0, rt tt YStT . By Ito’s lemma, we have 00 de e,d,0,; rt rt ttt YYtWtTY ,S where 2 2 10 ,lnSt SSS 2 , and where t W denotes the Wiener process under the risk neutral probability measure. We construct a trinomial tree as follows. Parting pe- riod 0,T into N parts and tTN . For every node Figure 2. Left and right tail plots for Nikkei 225 index. Copyright © 2013 SciRes. JMF  H. IWAKI, L. LUO 332 ,ni , , the value of 0,1,,;0, 1, 2,nNi Yt is given by 0 , niSiy with a constant . We set e, 3 rT yStS t to satisfy such constraints that every transition probability must be positive and that . ;,pnij Yt 0yN jumps from ,ni to three nodes; 1,,,1, ,1,,.nijnininijni Here the width of jump is given by ,jni ee ,, , rtrnt yni nt jni t y 1 , where a means the largest integer less than or equal to . At each node (, , the risk-neutral transition probability is given by a)ni (;,)pni j 22 2 2 22 2 2 ;, ee,, 1if , ee,, if ,, , 0oth rtrnt rtrn t pnij yni nttji jni y yni nttjijni jni y , erwise. Since the option price at the maturity is given by , where K denotes the strike price, and the risk-neutral transition probability has been calculated at every node, the current option price can be derived by cal- culating backwards from the final nodes to the initial node . ,max ,e ,0 rT CNjyNj K 0, 0C 0, 0 4.2. Data Description We use Nikkei 225 index call option prices for the em- pirical study. Options written on this index are the most actively traded European type contracts in Japan. We use daily closing prices of the premiums during October 2011. We also adopt three month TIBOR as the risk-free rate. For the simplicity we don’t adjust for dividends. We divide the option data into several categories according to either the moneyness or the term to expiration. As to the moneyness, we classify an option contract as at-the- money (ATM) if 0.97 1.03SK, out-of-the-money (OTM) if 0.97SK, in-the-money (ITM) otherwise. As to the term to expiration, we classify an option con- tract as short-term if days, medium-term if , long-term otherwise. Since the long term option contracts are traded scarcely, we exclude them from the test. 60T 60 180T 4.3. Parameter Estimation and In-Sample Fit In this section, we make some performance tests by comparing option pricing under the hybrid model with that under the BS model. We follow the approach taken by [10]. In order to apply the hybrid model for option pricing, we need to estimate the model parameters. Strike price K and time to maturity T are specified in the con- tract. We also know spot price S and interest rate r from the market. However, since structural parameters 1 and 2 are unobservable, we estimate them as fol- lows. First collect N prices of Nikkei 225 index call op- tions on a given day in October 2011. For each 1, ,nN , let n and n T be respectively the time to maturity and the strike price of the n-th option. Let K ˆ,, nn CtT n denote the observed market price and K,, nn CtT n be the model price. For each n, we define a function of 1 and 2 by 12 ˆ ,,,,, nnnnnn CtTKCtTK . n Then we estimate the parameters so as to minimize the sum of squared errors; 12 2 ,1 1 min, . N n n 2 (5) We employed the function optim in the R software to implement the minimization in Equation (5). Daily aver- ages of the estimated parameters are reported in Table 1 followed by the standard errors in the parentheses. denotes the total sum of squared errors and SSE SSE de- notes an average of in the sample period. SSE In general we can find the hybrid model improves the goodness of fit. In most of the trading days, the values of 1 are similar in two models and those of 2 are very small near to zero. It might indicate that the option prices are mostly determined by the BS model. This is not sur- prising because the most of the financial institutions quote the prices based on the BS model. We can find that the standard errors of 2 are significantly greater than those of 1 . This may be explained as follows. In dif- ferent days there are different market conditions not re- flected in the BS model but described by 2 . The values of 2 in the short term are larger than those in the long term. This is consistent with that the price feedback in volatility becomes larger and larger as time passes. of the hybrid model in the short term is better than that in the long term because option prices with the short term are affected heavily by the volatility fluctuations and the hybrid model can consider this kind of effect in option pricing. The performance among the out-of-the-money options is not as good as predicted, regardless to the time to maturities. However, we note that most of out-of-the- SSE Copyright © 2013 SciRes. JMF 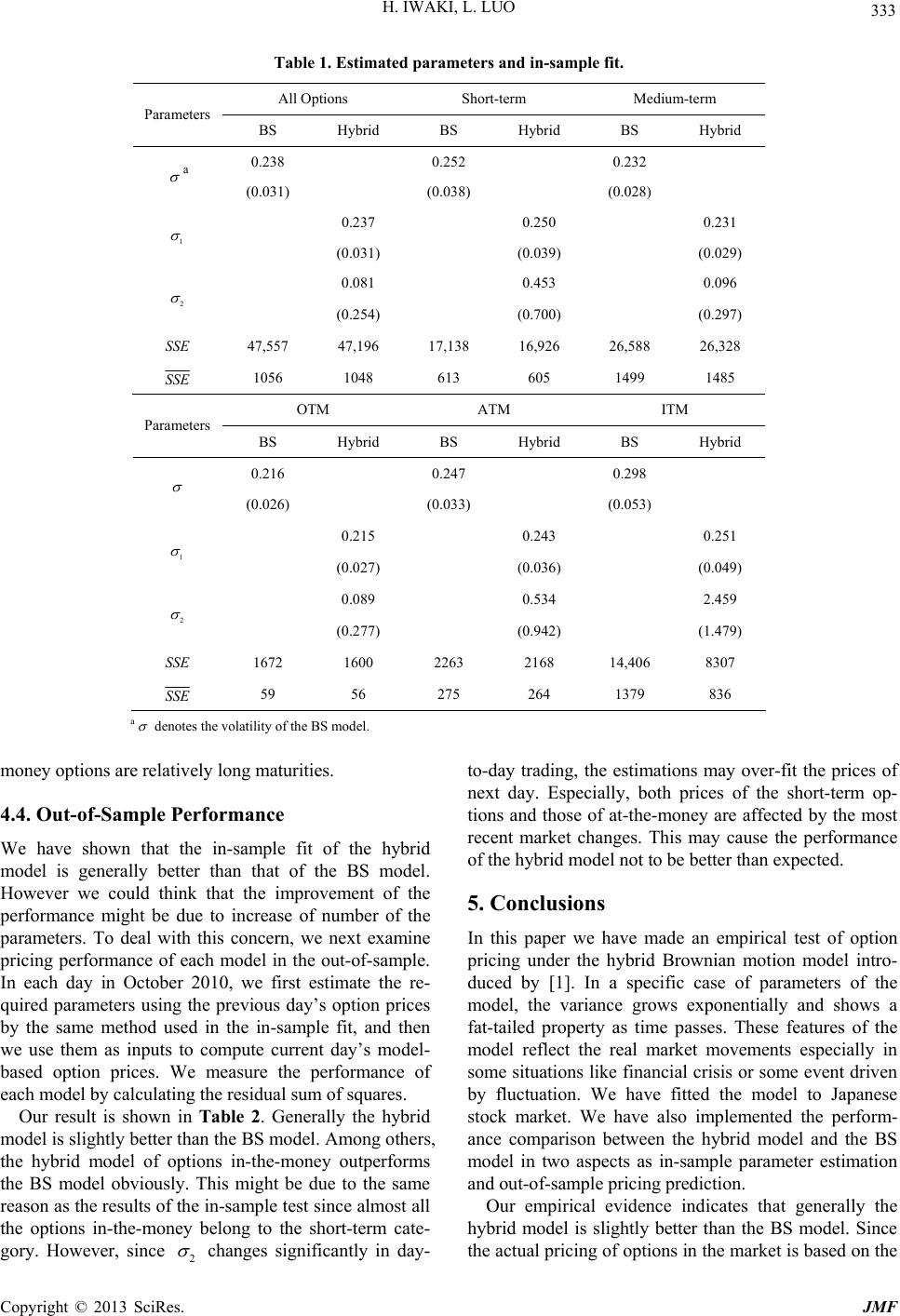 H. IWAKI, L. LUO Copyright © 2013 SciRes. JMF 333 Table 1. Estimated parameters and in-sample fit. All Options Short-term Medium-term Parameters BS Hybrid BS Hybrid BS Hybrid 0.238 0.252 0.232 a (0.031) (0.038) (0.028) 0.237 0.250 0.231 1 (0.031) (0.039) (0.029) 0.081 0.453 0.096 2 (0.254) (0.700) (0.297) SSE 47,557 47,196 17,138 16,926 26,588 26,328 SSE 1056 1048 613 605 1499 1485 OTM ATM ITM Parameters BS Hybrid BS Hybrid BS Hybrid 0.216 0.247 0.298 (0.026) (0.033) (0.053) 0.215 0.243 0.251 1 (0.027) (0.036) (0.049) 0.089 0.534 2.459 2 (0.277) (0.942) (1.479) SSE 1672 1600 2263 2168 14,406 8307 SSE 59 56 275 264 1379 836 a denotes the volatility of the BS model. money options are relatively long maturities. 4.4. Out-of-Sample Performance We have shown that the in-sample fit of the hybrid model is generally better than that of the BS model. However we could think that the improvement of the performance might be due to increase of number of the parameters. To deal with this concern, we next examine pricing performance of each model in the out-of-sample. In each day in October 2010, we first estimate the re- quired parameters using the previous day’s option prices by the same method used in the in-sample fit, and then we use them as inputs to compute current day’s model- based option prices. We measure the performance of each model by calculating the residual sum of squares. Our result is shown in Table 2. Generally the hybrid model is slightly better than the BS model. Among others, the hybrid model of options in-the-money outperforms the BS model obviously. This might be due to the same reason as the results of the in-sample test since almost all the options in-the-money belong to the short-term cate- gory. However, since 2 changes significantly in day- to-day trading, the estimations may over-fit the prices of next day. Especially, both prices of the short-term op- tions and those of at-the-money are affected by the most recent market changes. This may cause the performance of the hybrid model not to be better than expected. 5. Conclusions In this paper we have made an empirical test of option pricing under the hybrid Brownian motion model intro- duced by [1]. In a specific case of parameters of the model, the variance grows exponentially and shows a fat-tailed property as time passes. These features of the model reflect the real market movements especially in some situations like financial crisis or some event driven by fluctuation. We have fitted the model to Japanese stock market. We have also implemented the perform- ance comparison between the hybrid model and the BS model in two aspects as in-sample parameter estimation and out-of-sample pricing prediction. Our empirical evidence indicates that generally the hybrid model is slightly better than the BS model. Since the actual pricing of options in the market is based on the  H. IWAKI, L. LUO 334 Table 2. Out-of-sample pricing errors. All Options Short-term Medium-term BS Hybrid BS Hybrid BS Hybrid SSE 58,292 58,246 20,565 20,583 33,870 33,774 SSE 1297 1296 733 733 1935 1932 OTM ATM ITM BS Hybrid BS Hybrid BS Hybrid SSE 3646 3638 4928 4962 32,995 25,793 SSE 128 127 627 632 3082 2468 BS model, it is reasonable that the BS model fits the market data moderately. So it might be difficult to domi- nate the BS model remarkably. But if we can improve the algorithm of pricing method under the hybrid model, it might be possible to get better results. Furthermore, al- though we have made an empirical test using a special case of the hybrid model explained in Section 2.2 for the computational convenience, we might try to make similar tests using the general model of the hybrid Brownian motion in the near future. 6. Acknowledgements Hideki Iwaki is supported in part by Grant-in-Aid for Scientific Research (C) No. 22530310, Japan Society for the Promotion of Science. REFERENCES [1] W. T. Shaw and M. Schofield, “A Model of Returns for the Post-credit-crunch Reality: Hybrid Brownian Motion with Price Feedback,” Quantitative Finance, 2012, pp. 1- 24. doi:10.1080/14697688.2011.642810 [2] B. Mandelbrot, “The Variation of Certain Speculative Prices,” Journal of Business, Vol. 36, No. 4, 1963, pp. 394-419. doi:10.1086/294632 [3] E. F. Fama, “The Behavior of Stock-market Prices,” Journal of Business, Vol. 38, No. 1, 1965, pp. 34-105. doi:10.1086/294743 [4] R. C. Blattberg and H. J. Gonedes, “A Comparison of the Stable and Student Distributions as Statistical Models for Stock Prices,” Journal of Business, Vol. 47, No. 2, 1974, pp. 244-280. doi:10.1086/295634 [5] K. Aas and I. H. Haff, “The Generalized Hyperbolic Skew Student T-distribution,” Journal of Financial Eco- nometrics, Vol. 4, No. 2, 2006, pp. 275-309. doi:10.1093/jjfinec/nbj006 [6] Y. Nagahara, “Non-Gaussian Distribution for Stock Re- turns and Related Stochastic Differential Equation,” Asia- Pacific Financial Markets, Vol. 3, 1996, pp. 121-149. [7] M. Rubinstein, “Nonparametric Tests of Alternative Op- tion Pricing Models Using All Reported Trades and Quotes on the 30 Most Active CBOE Options Classes from August 23, 1976 through August 31, 1978,” Journal of Finance, Vol. 40, No. 2, 1985, pp. 455-480. doi:10.1111/j.1540-6261.1985.tb04967.x [8] J. Hull and A. White, “The Pricing of Options on Assets with Stochastic Volatilities,” Journal of Finance, Vol. 42, No. 2, 1987, pp. 281-300. doi:10.1111/j.1540-6261.1987.tb02568.x [9] S. Heston, “A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Cur- rency Options,” Review of Financial Studies, Vol. 6, No. 2, 1993, pp. 327-343. doi:10.1093/rfs/6.2.327 [10] G. Bakshi, C. Cao and Z. Chen, “Empirical Performance of Alternative Option Pricing Models,” Journal of Fi- nance, Vol. 52, No. 5, 1997, pp. 2003-2049. doi:10.1111/j.1540-6261.1997.tb02749.x [11] B. Dupire, “Pricing with a Smile,” Risk, Vol. 7, 1994, pp. 18-20. Copyright © 2013 SciRes. JMF
|