Energy and Power Engineering, 2010, 2, 306-312
doi:10.4236/epe.2010.24043 Published Online November 2010 (http://www.SciRP.org/journal/epe)
An Improved Catastrophic Genetic Algorithm and Its
Application in Reactive Power Optimization
Ouyang Sen
College of Electric Power, South China University of Technology
Guangzhou, China
Received April 22, 2010; revised June 19, 2010; accepted August 17, 2010
Abstract
This paper presents an Improved Catastrophic Genetic Algorithm (ICGA) for optimal reactive power opti-
mization. Firstly, a new catastrophic operator to enhance the genetic algorithms’ convergence stability is
proposed. Then, a new probability algorithm of crossover depending on the number of generations, and a
new probability algorithm of mutation depending on the fitness value are designed to solving the main con-
flict of the convergent speed with the global astringency. In these ways, the ICGA can prevent premature
convergence and instability of genetic-catastrophic algorithms (GCA). Finally, the ICGA is applied for
power system reactive power optimization and evaluated on the IEEE 14-bus power system, and the applica-
tion results show that the proposed method is suitable for reactive power optimization in power system.
Keywords: Genetic Algorithms, Reactive Power Optimization, Catastrophe, Power System
1. Introduction
The reactive power optimization (RPO), which is a non-
linear planning problem with the traits of discrete, multiple
variables and multiple constraints, has a significant influ-
ence on secure and economic operation of power systems.
It is an effective approach to improve voltage level, de-
crease network losses and maintain the power system run-
ning under normal conditions. In this field, many tradi-
tional methods have been used, including linear program-
ming (LP) [1], nonlinear programming (NLP) [2], and inte-
rior point methods (IPM) [3]. But, there are some draw-
backs in these conventional methods that can limit their
application in RPO, such as the complexity of algorithms,
poor convergence properties, and the difficulty of dealing
with dispersed variables.
Recently, Genetic Algorithm (GA) has been widely used
to RPO [4-7]. GA has been theoretically and empirically
proven to provide robust search in complex spaces. Nu-
merous papers and dissertations establish the validity of the
technique in optimization and control applications [8].
However, it is known that the main shortcoming of GA
is premature [9,10]. To overcome this, Genetic-Catastro-
phic Algorithm (GCA) is presented in [11], in which a new
operator, catastrophic operator, is proposed to recover the
population diversity when premature is happened.
Since the notion of GCA is proposed, there were several
researches. Meiying liao [12] analyze the mechanism of
catastrophic operator in GA, Yongjun Zhang [13] pre-
sented an improved catastrophic operator to enhance the
diversity of the small size populations. Others, GCA have
been successfully used in many fields of power system,
such as RPO [13], optimal power purchase planning [14]
and optimal configuration of switching devices in distribu-
tion system [15].
The GCA mentioned above is mainly concentrated on
improving the searching capability of SGA, but ignoring
the instability caused by catastrophic operator. In this paper,
based on the analysis of mechanism of GCA, an Improved
Catastrophic Genetic Algorithm (ICGA) is proposed. In
ICGA, a new catastrophic operator is designed for improv-
ing the stability of the proposed method, Besides, in order
to improve the GA’s convergent speed and searching capa-
bility, adaptive genetic algorithm (AGA) is also introduced
in this paper, in which crossover and mutation probabilities
are varied depending on the number of generations and the
fitness value, respectively.
An attempt to apply ICGA to RPO is presented in this
paper. The feasibility of the proposed algorithm for RPO is
demonstrated and compared with IEEE 14-bus systems.
The experimental results prove that the algorithm is rea-
sonable and practicable.

O. Y. SEN 307
This paper is organized as follows. Section 2 presents
brief reviews on Simple Genetic Algorithm (SGA), and
GCA, in Section 3, the ICGA method and the design of
crossover and mutation probabilities are proposed re-
spectively. In Section 4, a comparison among the ICGA,
SGA and AGA by using typical test function is con-
ducted. Then, the OPR model is mentioned in Section 5,
and the results of the simulation for IEEE 14-bus systems
are presented in Section 6. Finally a conclusion is pre-
sented in Section 7, and the end is references.
2. Genetic-Catastrophic Algorithm
GA, first proposed and investigated by John Holland in
1975 [16], is a robust probabilistic search and optimiza-
tion techniques based on the natural selection and genetic
production mechanism. Most of GA works are based on
the Goldberg’s simple genetic algorithm (SGA) frame-
work [17]. Typically, the process of SGA follows this
pattern [18]:
1) Initialization: Generate a first generation Np with
random parameters.
2) Evaluate all individuals of the generation Np
3) Selection: selects those offspring individuals with a
higher fitness value for the next generation Ns.
4) Crossover: crosses the selected best individuals to-
gether to get the new generation Nc.
5) Mutation: make random mutates of the Nc, and gets
new generation Nm.
6) Evaluate the individuals of the new generation Np,
and then go back to 3), until certain criteria (such as a
fixed number of generations. Or a time) are met.
The main difficulty of application of SGA in engi-
neering problems is premature, which occurs due to loss
of the population diversity. In order to avoid this prob-
lem and improve the convergence properties of SGA,
GCA is presented on the based of SGA. In GCA, when
premature is happened, catastrophic operator is employed
to regain the population diversity.
The process of GCA follows this pattern [11].
1) Initialization
2) Evaluation
3) Selection, Crossover and Mutation
4) If premature convergence occurs, apply catastrophic
operator, otherwise go to the step 5)
5) If the convergence criterion is satisfied, terminate
the calculation. If not, go to step 2).
The catastrophic operator includes catastrophic condi-
tion and operation, catastrophic condition is to judge
when to execute catastrophic operation. Generally, catas-
trophic operation includes two steps:
1) Remove a certain number (Nc) of individuals with
low fitness value in current population
2) Regenerate Nc individuals via various methods and
put into the current population to replace the removed
ones.
And the flow chart is shown in Figure 1.
Obviously, by adding various new individuals to the
current population, the diversity of population can great-
ly improve after employing catastrophic operator.
3. Improved Catastrophic Genetic
Algorithm
Although GCA is an effective method to overcome pre-
Figure 1. Flow chart of SGA.

O. Y. SEN 308
mature, the effect of catastrophic operator on GA’s con-
vergence properties is seldom researched. The following
subsections will discuss this in more detail.
3.1. Effect of Catastrophic Operator on GA’s
Convergence Properties
3.1.1. Effect of Traditional Catastrophic Condition on
GA’s Convergence Properties
Catastrophic condition is to decide when to execute cata-
strophic operation, Traditional catastrophic condition is
mainly based on the judge of premature convergence
[11,15], this method has following disadvantages:
1) Cause disruption of convergence because successful
convergence can still meet the catastrophic conditions.
2) Cause overly execution of catastrophic operation
because the condition is easily meet, it will bring about
the great increment of computing time.
3.1.2. Effect of Traditional Catastrophic Operation on
GA’s Convergence Properties
The key point of catastrophic operation contains two
aspects: give an appropriate value for N0 and decide how
to generate new individuals, in traditional catastrophic
operation, N0 is a constant value and the new individuals
are generated in these ways:
1) Sharply increasing mutation probability pm.
2) Remove most of the individuals except the fittest
one and randomly generate the new individuals.
These methods can critically affect the convergence
performance of GA:
1) Increase the randomness of GA search because the
new individuals are separated into the whole solution
space.
2) Prolong the convergence time because there are
many poor individuals in the new population, which can
disrupt the previous superior individuals when they are
selected to cross.
3) Disrupt the stability of GA at the late stage of evo-
lution because N0 is a constant value through whole
evolution process.
3.2. The Proposed Algorithm
In the previous subsection, it is saw that the traditional
catastrophic operator can disrupt the GA’s convergence
properties, and increase the randomness of GA due to
inappropriate design of catastrophic operator. In this
subsection, the analysis of relationship between the
evolution process and GA evolution process will be
firstly given. Then, the design of proposed method is
presented.
3.2.1. Analysis of Evolution Process and GA’s
Convergence Properties
In the whole GA evolution process, there are tradeoffs
that occur in exploration and exploitation. At the early
stage of evolution, to explore different solution space and
avoid premature, more emphasis should be put on the
exploration than exploitation. During the evolution, the
population will gradually converge to an optimum solu-
tion. At the late stage of evolution, increase exploitation
while decrease exploration will allow the GA to prevent
the converged optimum solution from disrupting.
As to catastrophic operator, the number of new gener-
ated individuals (Nc) is the source of exploration, Setting
Nc low allows the algorithm to exploit the superior indi-
viduals. Setting Nc high allows the algorithm to explore
different solution space.
3.2.2. Design of the Proposed Method
Above analysis inspire us that the convergence properties
of GA can be improved by varied Nc according to the
number of generation. Therefore, Nc is given as:
0
[exp(/ )]
cGen
NIntegerat TN

 (1)
Where Integer [] is a rounding sign, t is current gen-
eration, a is controlled parameter, TGen is maximum gen-
eration, N0 is maximum number of new generated indi-
viduals.
From the Equation (1), Nc is decreased by the number
of generation, it means that the exploration is also de-
creased by the number of generation while the exploita-
tion is on the opposite side. By this way, not only the
search ability but also the convergence properties of GA
can be enhanced,
The design of catastrophic condition and operation is
in the following details:
1) Catastrophic condition:
If (/ )0residual tT

&& tT, execute catastrophic
operation, where T is the generation steps.
2) Catastrophic operation:
Catastrophic operation is performed by the following
steps:
 Save the best individuals in current population
 Remove Nc individuals in current population
 Randomly generate Nc new individuals
 Add the new generated individuals to the current
population.
3.3. Design of Adaptive Crossover Probability
Mutation Probability
The choice of pc and pm is known to significantly affect
the performance of the GA, the pc controls the rate at
which solutions are subjected to crossover, the higher the

O. Y. SEN 309
value of pc the quicker are the new individuals intro-
duced into the population, vice versa. When a population
converges to a global optimal solution (or even a local
optimal solution), pc and pm increase and may cause the
disruption of the near-optimal solutions, therefore, it is
hoped that pc is given a high value to create more indi-
viduals at the early stage of evolution and maintaining
a relatively low value for the purpose of protecting supe-
rior individuals and algorithm’s stability at the late stage
of evolution process, in this paper, pc is gradually de-
creased depending on the number of generation in sig-
moid function form:
max min
min
()
() (2)
1exp( )
cc
cc
Gen
Gen
PP
Pt P
AT t
T




(2)
where pc(t) is crossover probability generation in t gen-
eration, Pcmax is maximum crossover probability, Pcmax is
minimum crossover probability and A is assigned
9.903438.
Mutation operator is used to maintain genetic diversity
from one generation of a population of chromosomes to
the next, the choice of pm is critical to GA performance,
large values of pm transform the GA into a purely random
search algorithm, In this paper, pm is varied adaptively
depended on both the number generation and every fit-
ness value of individual:
max min
min
()
(2)
1exp( )
max imm
mt m
Gen
max
Gen
f-f(X)PP
P exp()P
AT t
f
T

 


(3)
where Pm(t) is mutation probability of individual Xi in t
generation, Pmmax is maximum mutation probability,
Pmmax is minimum mutation probability, A is assigned
9.903438.
4. Performance Measures
In this section, the experiments that are conducted to
compare the performance of the ICGA, SGA and AGA
[19] are discussed. In order to test these methods’ con-
vergent speed, the average number of generations that
these GA methods require to generate a solution with a
certain high fitness value and the average consumed
times are taken into consideration. These can be obtained
by performing the experiment repeatedly (in our case,
100 times). To measure the convergence probability of
these methods, the number of instance (in 100 trials) for
which the GAs have successfully converged to the given
optimal solution is also employed.
4.1. Test Functions
In this research, the following multimodal functions with
varying complexities are used [19]:
22 2
11 2121
( ,)100()(1)
2.0482.048 (1,2)
i
f
xxxxx
xi


 

 (4)
22 2
12
212 222
12
sin
(, ) 0.5[1.0 0.001()]
10010 0(1,2)
i
xx
fxx xx
xi



 

(5)
Function f1 is a two-dimension function and has only
one minimum in its whole solution space. But it is an
abnormal function and is not optimized easily. Its global
minimum is f1(1,1)) = 0; Function f2 is a rapidly varying
multimodal function with two variables, and is symmet-
ric about the origin with the height of the barrier between
innumerable adjacent minima increasing as the global
optimal solution is approached. f(0,0) = 0 is its global
minimum.
4.2. Experiment Results
In all our experiments, the population size for all func-
tions is 64 and TGen is given 100, For the SGA, Pc = 0.9,
Pm = 0.1, For the AGA, k1 = k3 = 1, k2 = k4 = 0.5, Pcmax
= 0.9, Pcmin = 0.5, Pmmax = 0.1, Pmmin = 0.01. And for the
ICGA, Pcmax = 0.9, Pcmin = 0.5, Pmmax = 0.1, Pmmin = 0.01,
a = 10, N0 = 59. The algorithm will be stop when each
GAs attaining a solution with an objective functional
value of f1 (f2) equal to the threshold 0.0001, the ex-
perimental results are presented in Table 1:
As Table 1, both average generation and consumed
time of ICGA are less than SGA and AGA, Others, the
convergence times of ICGA is the best, it indicates that
ICGA can effectively ‘jump’ from the local optimum.
5. Reactive Power Optimization Model
RPO is mainly implemented by setting generator bus
voltages, VAR compensators and transformer taps. The
core of the RPO problem is to determine the reasonable
reactive power compensation point and the best com-
pensation capacity, than it can minimize the real power
losses and improve voltage profile. The models of reac-
tive power optimization are described as follows:
5.1. Objective Function
1
(cossin)
N
lossjj ijijijij
ijh
PVVG B




 (6)

O. Y. SEN 310
Table 1. Comparison of performance of SGA, AGA and ICGA.
Function Average Generations Convergence Times Consumed Time
f1 SGA 91 AGA 61 ICGA 41 SGA 82 AGA 92 ICGA 97 SGA 0.47 AGA0.36 ICGA 0.28
f2 48 35 28.9 71 91 99 0.39 0.32 0.22
where Ploss is net loss for meritorious indicators, N is the
number assemble of transmission lines in the network, Vi
is the voltage value at bus i, Vj is the voltage value at bus
j, δij is the phase-angle difference of the voltage value
between bus i and j, Gij and B ij are admittance matrix
elements in the real and imaginary parts.
5.2. Constraints
1
1
(cos sin)
(sin-cos)
N
ii jijijijij
j
N
ii jijijijij
j
PV VGdBd
QV VGdBd











(7)
where Pi, Qi, Vi is active power, reactive power and
voltage of node i respectively.
Variable equation:
Power system safe operation must be made within the
scope. Select capacitive reactive power compensation
capacity Ci, adjustable transformer tap position Tj and
generator terminal voltage V
gk as the control variables.
And select and Node voltage amplitude Vi as state vari-
ables reactive power generators Qgj..
min max
min max
min max
iii
jjj
gkgk gk
CCC
TTT
VVV





(8)
The unequal constraint (9) is the unequal constraint of
the control variable vector, where Tjmin, Timax is adjustable
load transformer tap position of the upper and lower limit.
Cimin, Cimax is capacitive reactive power compensation
capacity of the upper and lower limit; Vgkmin, Vgkmax is
generator terminal voltage the upper and lower limits.
min max
min max
iii
gjgj gj
VVV
QQQ





 (9)
The unequal constraint (10) is the unequal constraint
of dependent variable vector, where Vimin, Vimax are the
node voltage amplitude of the upper and lower limit.
Qgjmin, Qgjmax are the limits of generators reactive power.
The control variables are self-constrained and dependent
variables are constrained by adding them as penalty
terms to the objective function (Equation (1)). So the
objective function is changed to:
22
()( )
max minmaxmin
min loss
Q
Vgi
i
VQ
VVQ Q
i igigi
P 






(10)
where λV and λQ are penalty factors; ΔVi and ΔQgi are the
violations of load-bus voltages and generators reactive
power, respectively, defined as:
min min
min max
max max
0
iiii
iiii
iii i
VVVV
VVVV
VVV V



 



(11)
min min
min max
max max
0
gigi gigi
gigigi gi
gi giigigi
QQQQ
QQQQ
QQQ Q


 



(12)
6. Numerical Results
The study is implemented using Matlab and tested on an
IEEE 14-bus system, which includes three transformers,
two generators and three compensation points. The step
size of reactive power compensation and transformer tap
ratios is 0.05 pu and 0.0125 pu respectively. Capacity
ceiling of Reactive compensation device is 0.5 pu, and
the step is 0.01 pu. The control variables are showed as:
Y= [UG1 U
G2 Q G3 Q G6 Q G8 T 47 T 49 T 56]. Details of this
system and parameters are given in [20]. The number of
generation is 30 and other parameters are following: TGen
= 30, N0 = 29, λV = 15, λQ = 1.5.The best optimization
results of SGA, ICGA and GCA are given in Table 2,
which are obtained from different kinds of algorithm
respectively performing 30 times.
As Table 2, the initial generator reactive power QG2
and load voltages VD3~VD14 are outside their limits, after
optimization by the three methods, all the state variables
are regulated back into their limits, besides, Ploss is de-
creased to 0.1375 by ICGA while that of 0.1378 by GCA
and 0.1385 by SGA, thus, ICGA may find better out-
come than the rest kinds of methods.
Table 3 shows the comparison of the best, worst, av-
erage and standard deviation values for different methods.
Due to probabilistic characteristic of evolutionary algo-
rithms, results reported here correspond to average from
30 trials.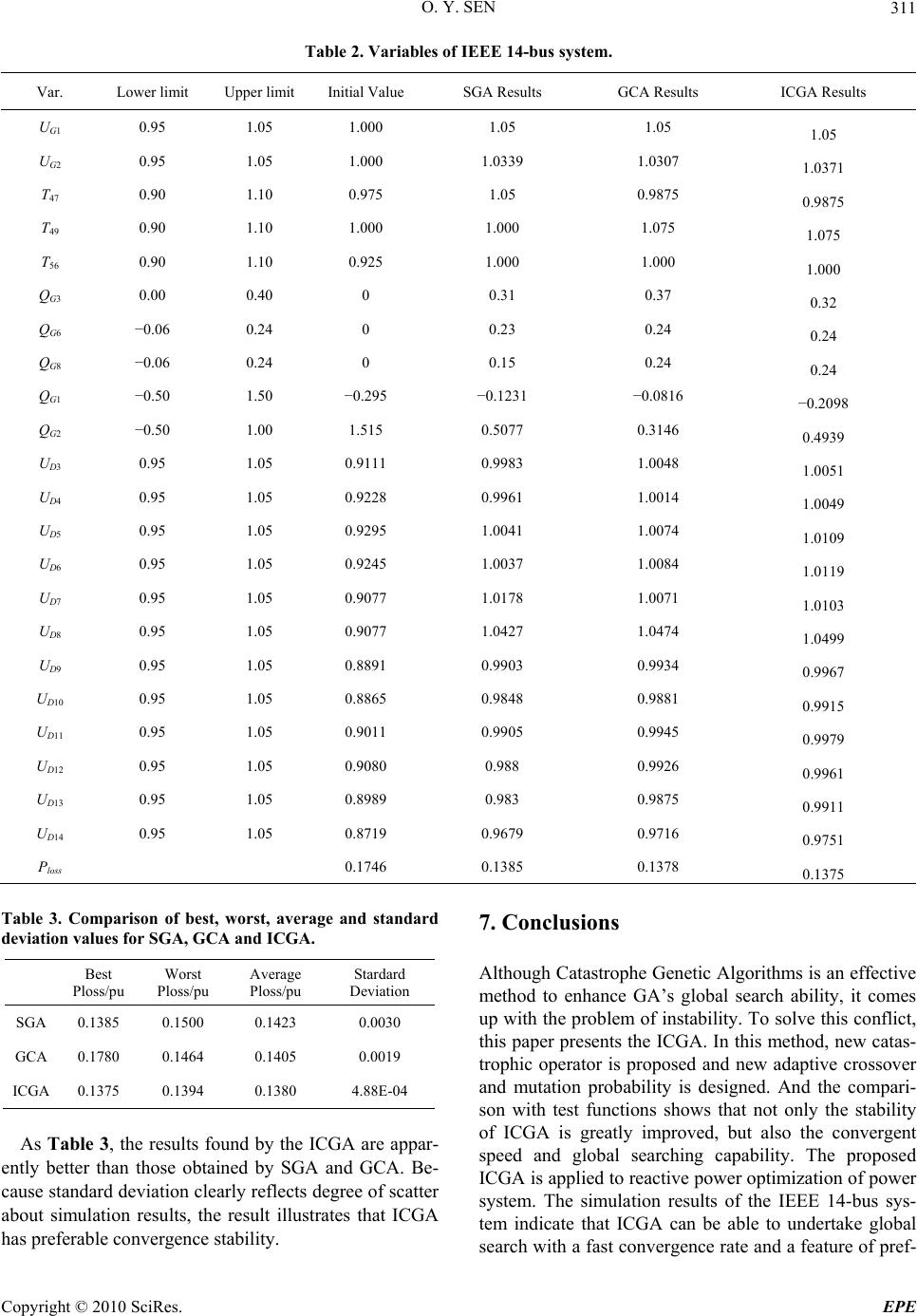

O. Y. SEN 311
Table 2. Variables of IEEE 14-bus system.
Var. Lower limit Upper limit Initial Value SGA Results GCA Results ICGA Results
UG1 0.95 1.05 1.000 1.05 1.05 1.05
UG2 0.95 1.05 1.000 1.0339 1.0307 1.0371
T47 0.90 1.10 0.975 1.05 0.9875 0.9875
T49 0.90 1.10 1.000 1.000 1.075 1.075
T56 0.90 1.10 0.925 1.000 1.000 1.000
QG3 0.00 0.40 0 0.31 0.37 0.32
QG6 −0.06 0.24 0 0.23 0.24 0.24
QG8 −0.06 0.24 0 0.15 0.24 0.24
QG1 −0.50 1.50 −0.295 −0.1231 −0.0816 −0.2098
QG2 −0.50 1.00 1.515 0.5077 0.3146 0.4939
UD3 0.95 1.05 0.9111 0.9983 1.0048 1.0051
UD4 0.95 1.05 0.9228 0.9961 1.0014 1.0049
UD5 0.95 1.05 0.9295 1.0041 1.0074 1.0109
UD6 0.95 1.05 0.9245 1.0037 1.0084 1.0119
UD7 0.95 1.05 0.9077 1.0178 1.0071 1.0103
UD8 0.95 1.05 0.9077 1.0427 1.0474 1.0499
UD9 0.95 1.05 0.8891 0.9903 0.9934 0.9967
UD10 0.95 1.05 0.8865 0.9848 0.9881 0.9915
UD11 0.95 1.05 0.9011 0.9905 0.9945 0.9979
UD12 0.95 1.05 0.9080 0.988 0.9926 0.9961
UD13 0.95 1.05 0.8989 0.983 0.9875 0.9911
UD14 0.95 1.05 0.8719 0.9679 0.9716 0.9751
Ploss 0.1746 0.1385 0.1378 0.1375
Table 3. Comparison of best, worst, average and standard
deviation values for SGA, GCA and ICGA.
Best
Ploss/pu
Worst
Ploss/pu
Average
Ploss/pu
Stardard
Deviation
SGA 0.1385 0.1500 0.1423 0.0030
GCA 0.1780 0.1464 0.1405 0.0019
ICGA 0.1375 0.1394 0.1380 4.88E-04
As Table 3, the results found by the ICGA are appar-
ently better than those obtained by SGA and GCA. Be-
cause standard deviation clearly reflects degree of scatter
about simulation results, the result illustrates that ICGA
has preferable convergence stability.
7. Conclusions
Although Catastrophe Genetic Algorithms is an effective
method to enhance GA’s global search ability, it comes
up with the problem of instability. To solve this conflict,
this paper presents the ICGA. In this method, new catas-
trophic operator is proposed and new adaptive crossover
and mutation probability is designed. And the compari-
son with test functions shows that not only the stability
of ICGA is greatly improved, but also the convergent
speed and global searching capability. The proposed
ICGA is applied to reactive power optimization of power
system. The simulation results of the IEEE 14-bus sys-
tem indicate that ICGA can be able to undertake global
search with a fast convergence rate and a feature of pref-

O. Y. SEN 312
erable convergence stability. It is proved to be efficient
and practical during the reactive power optimization.
8. References
[1] K. R. C. Mamandur and R. D. Chenoweth, “Optimal
control of reactive power flow for improvements in volt-
age profiles and for real power loss minimization,” IEEE
Transaction on PAS, Vol. 100, No. 7, 1981, pp. 3185-
3194.
[2] L. C. Li, J. Y. Wang, L. Y. Chen, et al., “Optimal reactive
power planning of electrical power system,” Proceedings
of the CSEE, Vol. 19, No. 2, 1999, pp. 66-69.
[3] M. B. Liu and X. C. Wang, “An application of interior
point method to solution of optimization problems in
power systems,” Power System Technology, Vol. 23, No.
8, 1999, pp. 61-64, 68.
[4] K. J. Iba, “Reactive Power Optimization by Genetic Al-
gorithm,” IEEE Transactions on Power System, Vol. 9,
No. 2, 1994, pp. 685-692.
[5] P. Nallagownden, L T. Thin and N. C. Guan, “Applica-
tion of Genetic Algorithm for the Reduction of Reactive
Power Losses in Radial Distribution System,” IEEE In-
ternational Conference on Power and Energy, Vol. 26,
No. 5, 2006, 76-81.
[6] P. Sreejaya and R. Rejitha, “Reactive power and Voltage
Control in Kerala Grid and Optimization of Control
Variables Using Genetic Algorithm,” IEEE International
Conference on Power System Technology, 2008, 1-4.
[7] H. W. Yan and J. N. Tao, “Reactive power optimization
research of power system considered the generation
transmission and distribution,” IEEE International Con-
ference on Industrial Technology, Chengdu, 2008, pp.
1-4.
[8] D. E. Goldberg and P. Segrest, “Finite Markov chain
analysis of genetic algorithms,” Proceedings of 2nd In-
ternational Conference Genetic Algorithms, 1987, pp.
1-8.
[9] J. E. Baker, “Reducing bias and inefficiency in the selec-
tion algorithm,” Proceedings of the 2nd Annual Confer-
ence on Genetic Algorithms, Massachusetts Institute of
Technology, Cambridge, 1985, pp. 14-21.
[10] D. E. Goldberg, “Genetic algorithms and rule leaming in
dynamic system control,” Proceedings of International
Conference on Genetic Algorithms and Their Applica-
tions, Pittsburgh, 1985, pp. 8-15.
[11] X. D. Jin and Z. Li, “Genetic-Catastrophic Algorithms
and Its Application in Nonlinear Control System,” Jour-
nal of System Simulation, Vol. 9, No. 2, 1997, pp. 111-
115.
[12] M. Y. Liao and Y. J. Zhang, “Study on the Effect of Cata-
clysm Operator on Genetic Algorithm,” Computer Engi-
neering and Application, Vol. 41, No. 13, 2005, pp. 54-
56.
[13] Y. J. Zhang, Z. Ren, H. M. Zhong, Z. Y. Tang and C.
Shang, “Cataclysmic Genetic Algorithms Based Optimal
Reactive Power Planning,” Automation of Electric Power
Systems, Vol. 26, No. 23, 2002, pp. 29-32.
[14] Y. J. Zhang, W. G. Yuan, B. F. Li and M. C. Liao, “Op-
timal Power Purchase Planning of Hainan Power Grid
Company,” The 8th International Power Engineering
Conference, December 2007, Singapore, pp. 1854-1858.
[15] D. Wang, Y. K. Shi, J. Y. Cong, H. Sun and J. Y. Zou,
“Application of Catastrophic Genetic Algorithm to the
Opitmal Configuration of switching Devices in Distribu-
tion System,” High Voltage Apparatus, Vol. 40, No. 3,
2004, pp. 180-182.
[16] J. H. Holland, “Adaptation in natural and artificial sys-
tems,” University of Michigan Press, Ann Arbor, 1975.
[17] D. E. Goldberg, “Genetic Algorithms in Search, Optimi-
zation and Machine Learning,” Addison-Wesley Pub-
lishing Company Inc., Massachusetts, 1989.
[18] L. Davis, Ed., “Genetic Algorithms and Simulated An-
nealing,” Pitman, London, 1987.
[19] M. Srinivas and L. M. Patnaik, “Adaptive probabilities of
crossover and mutation in genetic algorithm,” IEEE
Transactions on System, Man and Cybernetics, Vol. 24,
No. 4, 1994, pp. 656-667.
[20] Y. J. Zhang, “Cataclysmic Genetic Algorithm and MAS
Based Model for Reactive Power Optimization for Power
System,” Ph.D. Dissertation, South China University of
Technology, Guangzhou, 2004.