Paper Menu >>
Journal Menu >>
 Energy and Power Engineering, 2010, 2, 298-305 doi:10.4236/epe.2010.24042 Published Online November 2010 (http://www.SciRP.org/journal/epe) Copyright © 2010 SciRes. EPE Thermodynamic and Experimental Analysis of an Ammonia-Water Absorption Chiller Dingfeng Kong, Jianhua Liu, Liang Zhang, Hang He, Zhiyun Fang School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai, China E-mail: kongdingfeng2002@163.com Received August 4, 2010; revised September 15, 2010; accepted October 16, 2010 Abstract A single stage ammonia-water absorption chiller with complete condensation is designed, built and tested. The apparatus is designed for a cooling capacity of 2814 W, which is obtained using electric heater as heat- ing source. The thermodynamic models have been derived using the First and Second Laws. Calculated re- sults are compared with experimental data. The results show that the cooling capacity of experimental appa- ratus is found between 1900 and 2200 W with the actual coefficient of performance (COP) between 0.32 and 0.36. The contribution of the components to internal entropy production is analyzed. It shows that the larger irreversibility is caused by spanning the largest temperature and dissipated thermal energy by heat transfer losses at the generator and evaporator. In the experimentation, the low pressure is lower than the designed value. This is a consequence of a large capacity in the falling film absorber which performs as expected. This decreases the evaporation pressure, and the evaporating temperature could be reduced to the designed value. Keywords: Absorption Chiller, Ammonia-Water, Thermodynamic Modeling, Experimental, Performance 1. Introduction Widespread efforts are currently underway to utilize available energy resources efficiently by minimizing waste energy and develop replacements for the tradition- ally refrigerants (CFCs and HCFCs), which contribute to ozone depletion and greenhouse warming. Absorption chillers which are heat-powered refrigeration systems have got more and more attention, due to the recognition of rational utilization of energy and the concerns about ecological problem. The ammonia-water mixture is environmental friendly, which is the only working pair currently used for refrig- eration purposes in absorption systems, and despite of the new mixtures under investigation, the ammonia-water mixture is the only one with a clear future [1]. The prin- ciple of the absorption is providing the necessary pres- sure difference between the vaporizing and condensing processes, which alternately condenses under high pres- sure in the condenser by rejecting heat to the environ- ment and vaporizes under low pressure in the evaporator by absorbing heat from the medium being cooled. Am- monia-water absorption chillers have been widely used in many occasions [2]. Amount of work associated with theoretical and ex- perimental analysis of the commercial absorption chillers, using ammonia-water as the working fluid, is available in the literature [3,4]. There are three classical kinds of en- doreversible modeling in previous approach [5-9]. K. C. Ng et al. presented an explicit irreversible thermody- namic model, which considered external and internal losses, to permit easy determination of optimal operating conditions of chiller, as well as a predictive and diagnos- tic capability [10-14]. Via comparison with actual data of an absorption chiller, firstly, it clearly demonstrated that all endoreversible models fail to capture part of the key losses which contribute to the chiller COP. By account- ing for only the external irreversibilities, they over pre- dict the chiller COP by as much as 160-180%. Secondly, endoreversible models portray an incorrect trend for COP in the upper region of the characteristic plot, which also predicts no maximum for the COP at the practical cooling range of absorption chillers. The reasons for this is all endoreversible models ignore the presence of in- ternal losses stemming from heat and mass transfer in the generator and absorber, internal regeneration and throt- tling. A key element of accounting for internal entropy production is the use of a process average temperature to The research is funded by The Innovation Fund Project for Graduate Student of Shanghai (JWCXSL0901)  D. F. KONG ET AL. Copyright © 2010 SciRes. EPE 299 analyze energy and entropy flows. An accurate process average temperature is essential to perform chiller diag- nostics, or predict chiller performance under different operating conditions, or evaluate efficiency improve- ments that would derive from diminishing a given source of irreversibility. H. T. Chua et al. developed a general definition of the process average temperature. It is based on the method of computing for the process average temperature for the evaporator, condenser, generator and absorber [15]. However, most of the research is carried out with commercially fashioned chillers that have been specifi- cally designed as an air-cooled system. To investigate the system characteristics being consistent with the reality, an experimental apparatus is designed and fabricated, using the irreversible thermodynamic model. All air- cooled components are replaced by water-cooled com- ponents, and variation of some operating parameters should be carried out. The model considers both the ex- ternal and internal losses in ammonia-water absorption chiller to accurately predict the chiller COP at its nomi- nal range of cooling capacity. 2. Experimental Testing of the Apparatus 2.1. Description of the Apparatus An experimental apparatus has been designed and built to study the performance of a single stage ammonia– water system with complete condensation. A schematic diagram and a photograph of the experimental apparatus are shown in Figure 1. The major components are the generator, vertical sieve tray tower with complete con- densation (VST), absorber, condenser, evaporator, solu- tion heat exchanger (SHE), subcooler, ammonia fluid reservoir (AFR), solution fluid reservoir (SFR), pump and refrigerant expansion device (RED) and weak solu- tion expansion device (SED). The ammonia-water mixture is heated in the generator Pump 1 Generator VST Condenser SHE Absorber Subcooler Evaporator SFR AFR Cooling water SED RED Control valve 1 1 2 5 3 4 6 9 10 10a 11 12 12a 78 Pump 2 Control valve 2 Figure 1. A schematic diagram of the apparatus. State points are same in figures and tables below.  D. F. KONG ET AL. Copyright © 2010 SciRes. EPE 300 by electric heater, which is equipped with three sets of electric resistances, 3000 W each. The heater power can be adjusted and controlled. The heat power reaches val- ues of up to 9000 W. An electro connecting pressure gauge is installed in the generator. For normal operating conditions, the system high pressure side is approxi- mately 14 bar. The electric heater is turned off under the conditions of more than 23 bar. Then ammonia vapour is separated, but it is mixed up with fractions of water va- pour. The purification process is carried out by a VST, where a counter-current contact is established between an upward vapour flow and a downward liquid flow. The VST is built with the seamless tube in Steel ASTM 1020 of 68 mm inner diameter and a total length of 1800 mm, divided into 6 sections, in order to disas- semble conveniently, 300 mm each. Two pairs of 10 mm thick Pyrex glasses are installed in each section mounted on 102 mm from bottom, which allow checking if flood- ing inside the VST occurs. To reduce heat losses to the environment, the stripping section of VST and generator are insulated with a mineral wool preformed pipe of thickness 15 mm. The vapour enriched in ammonia content leaving the VST is condensed in a plate type condenser, cooled by water, which removes heat from the gas mixture and the vapour is condensed to a liquid. After the vapour is com- pletely condensed, the liquid leaves the condenser and passes to the subcooler. The subcooler is a shell and tube heat exchanger, which reduces the temperature of the liquid. When the liquid mixture leaves the subcooler, the pressure drops as it passes through a RED into the evaporator. After leaving the evaporator, the vapour is further heated as passing through the subcooler to the absorber. The high pressure weak solution leaving the generator enters a SHE. Finally, the weak solution passes through a SED and enters into the absorber with the re- frigerant vapour coming from the subcooler. Then the vapour is absorbed into the weak solution from the gen- erator in the water-cooled absorber, which is a falling film type. The strong solution is now at the lower cycle pressure, and it must be sent to the stripping section. This is achieved by a diaphragm pump. Then the cycle is completed. 2.2. Data acquisition System The experimental apparatus has been equipped with an acquisition data system based on a PC and an acquisition data card. Refrigerant, absorbent temperatures are col- lected from PT-100 probe with accuracy of ±0.15 K. Pressures are obtained from piezoelectric transducers with an accuracy of ±0.2 bar. The cooling water flow rate in the condenser and absorber is measured by means of a rotary flowmeter with an accuracy of ±0.2%. The rest of flow rate in the apparatus is measured by means of a Coriolis sensor with accuracy of ±0.1% and elec- tromagnetic turbine sensors with an accuracy of ±0.3%. Concentrations of the binary mixture are determined by titration with an uncertainty of ±4%. Before experimen- tation, the entire instruments have been calibrated. Evaporation and condensation temperatures, high and low pressures, and concentration are recorded. 2.3. Experimental Procedure After the system is evacuated with a vacuum pump, the SFR and generator are filled with 120 l of aqueous solu- tion of ammonia with mass concentration of 0.40. All valves on the apparatus are closed. The required experi- mental generation heat value is of 6000 W. In order to generate the needed temperature, it is needed to adjust the power of electric heater. The rate of heating is con- trolled below 363 K/h. When the generation pressure is raised in the scope of 6-7 bar, the SED and pump 1 are opened to start the cycle of ammonia-water solution. The cooling water valve of condenser is opened, when gen- eration pressure gradually equals to condensing pressure. Then the valve through the vapour on the top of VST is opened. The cooling water flow is adjusted to control pressure of VST whenever necessary. The quantity of reflux is controlled to avoid for weeping or flooding. The RED is opened as the liquid mixture passes into the evaporator. The suction valve of saturated vapour leav- ing from evaporator on the absorber is opened, while the cooling water valve of absorber is opened. The absorbent pressure and absorbent temperature are controlled to de- signed values by adjusting cooling water flow on ab- sorber. The cooling capacity is determined using a calo- rimetric measuring procedure based on the regulations of the thermal balance. In each test, a 120 kg of fresh water in a thermal balance water box is kept at 293 K. An aquarium pump is used to circulate the water. Once the apparatus has reached the steady state, all test data are recorded by the data acquisition system. 3. Mathematical Model A mathematical model is developed to analyze the per- formance of the experimental system. Temperatures and pressures of working fluid are based on designed values. Water and ammonia properties are obtained from stan- dard properties of pure substances table in the ASHRAE [16]. Specifically, ammonia-water properties are based on procedures developed by Tillner-Roth and Friend [17].  D. F. KONG ET AL. Copyright © 2010 SciRes. EPE 301 3.1. First and Second Law Analysis The thermodynamic models of components ensure en- ergy balance, mass balance and entropy production ap- plying the Second Law of Thermodynamics. With the expression for heat transfer rate i Q, the thermal con- ductance of component is calculated from 1 [()() ] j iinout Qmhmh (1) int i S represents the summations of the entropy genera- tion due to heat and mass transfer in the certain compo- nent. int / iiiiiii out in SmsmsQT (2) From Equation (2), an accurate process average tem- perature i T is essential as defining and deriving int i S, which translates into accurate evaluation of heat ex- changer effective thermal conductance. i T is intent upon performing chiller diagnostics, or predicting chiller performance under different operating conditions, or evaluating efficiency improvements that would derive from diminishing a given source of irreversibility. (/) i dH TdH T (3) From Equation (3), i T is computed from the properly weighted piecewise compilation of measured tempera- tures along nonisothermal paths. In practical situations, the thermodynamic system is expected to relate to as an effective blackbox which can be probed from the outside only, i.e., for which only nonintrusive measurements at the inlets and outlets are realistic. These claims were demonstrated in Ref. 18. So the correct process average temperature should be calculated using experimental measurements and basic thermodynamic analysis for ammonia-water absorption chiller. All the terms on the right hand side of Equation (3) can be computed from the thermodynamic properties of the refrigerant if the local pressures and temperatures at the inlets and outlets are known. 3.2. Assumptions It is saturated state, when the weak solution leaves the generator at the generation temperature. The refrigerant leaves the condenser at the con- densing temperature as saturated liquid. The refrigerant leaving the evaporator is evapo- rated completely as saturated vapour. The strong solution leaves the absorber at the ab- sorbent temperature as saturated liquid. The energy balances do not contain the heat losses in the VST, so the effect of VST is neglected. Applying Equations (1) and (2) for each component, the heat transfer rates and entropy generation are sum- marized in Table 1 below. 3.3. System Thermal Balance The internal energy and the entropy of the working fluids in the absorption cycle are written as follows: intint int int int intint totgcaeSHE sc int intint PSEDRED S SSSSSS SS S (4) 3.4. Coefficient of Performance The general refrigeration system can be considered as a perfectly reversible system, the net refrigerating effect is the heat absorbed by the refrigerant in the evaporator. The theoretical COP is given by e th g COPQ Q (5) In the absorption refrigeration system, the total energy supplied to the system is the total of the heat supplied in the generator and work done by the pump. The actual COP of the ammonia-water absorption chiller is calcu- lated from e gP COP Q QW (6) 4. Discussion 4.1. Comparison between Actual and Calculated Performance Table 2 tabulates the summary of heat transfer rates and performance parameters of the apparatus. The actual COP decreases reaching values of 90% at the theoretical COP of 0.469. Therefore the work of the pump can not be neglected when considering the performance of ab- sorption chiller. Referring to the Figure 2, the actual results are found to lie between 75% and 85% of the calculated values. The difference may result from heat loss from the gen- erator, low concentration and large resistance of refrig- erant and supercooling degree does not meet the re- quirements, etc. When deciding which one is main factor, multiply the surface area of the generator with the dif- ference between the temperature of the surrounding and that of the generator. Then divide the result with the ad-  D. F. KONG ET AL. Copyright © 2010 SciRes. EPE 302 Table 1. Summary of first and second law relations for each component of the apparatus. Component Mass balance Energy balance Entropy generation Generator 47 8 mmm 44 7788 mx mxmx g447788 Qmhmhmh int g447788gg /SmsmsmsQT Condenser 910 mm c9910 Qmh-h int c9109cc ()/SmssQT- Absorber 612a 1 mm m 66 12a12a11 mxm xmx a661212 11aa Qmhmh mh int a11661212aa / aa SmsmsmsQT Evaporator 11 12 mm e121211 Qmh-h int e121211ee ()/SmssQT- SHE 23 mm45 mm SHE3 3 24 4 5 Qmhhmhh-- int SHE2 2435 ()Smssss+- Subcooler 10 10a mm1212a mm sc101010a12 12a 12 Qmhh mhh-= - int sc10 10a12a1012 ()Smssss+- Pump 1 12 mm P2211 Wmhmh int P221P ()SmssW- SED 56 mm RED5 56 6 Qmhmh= int SED565 ()Smss- RED 10a 11 mm RED10a10a11 11 Qmhmh= int RED10a 11 10a ()Smss- Table 2. Properties of the various state points for the chiller. State h (kJ/kg) m (kg/s) P (bar) T (K) x (kg/kg) s(kJ/kg·K) 1 65 0.01756 2.06 309 0.40 0.7647 2 65 0.01756 14.37 309 0.40 0.6493 3 326 0.01756 14.37 363 0.40 1.854 4 430 0.01481 14.37 393 0.29 1.858 5 100 0.01481 14.37 319 0.29 0.649 6 100 0.01481 2.06 319 0.29 0.6497 7 1830 0.00274 14.37 368 0.95 5.6577 8 350 0.01781 14.37 368 0.40 1.4752 9 1680 0.00274 14.32 318 0.998 5.9196 10 500 0.00274 14.32 318 0.998 1.7853 10a 414 0.00274 14.32 313 0.998 1.6321 11 414 0.00274 2.36 258 0.998 1.6415 12 1440 0.00274 2.36 258 0.998 6.3315 12a 1526 0.00274 2.36 293 0.998 6.5272 Summary of heat transfer rates and performance parameters of the apparatusCOP0.424 th COP 0.467 P636WW sc 236WQ SHE 4300WQ g6000WQ e2814WQ a4526WQ c4100WQ. dition of the ratio of the thickness of the generator and thermal conductivity of the generator and that of the thickness of the insulation material and thermal conduc- tivity of the insulation material. It can be seen that, the heat loss from the generator is the main reason of the difference. In the experimentation, adjust the flow of refrigerant by changing the opening of RED to ensure the constant temperature level of the generator along with increasing the heat load. The calculated cooling capacity increases almost linearly with the generator heat input. It is dis- covered that to operate the experimental apparatus there is a minimum generator input (around 4800 W). When the heat input is lower than the minimum value, the sys- tem is not able to produce any cooling capacity. To ob- tain a rectifying effect, a minimum vapour generated is required. Then the vapour rises through the VST and flows counter-currently with a liquid introduced at the 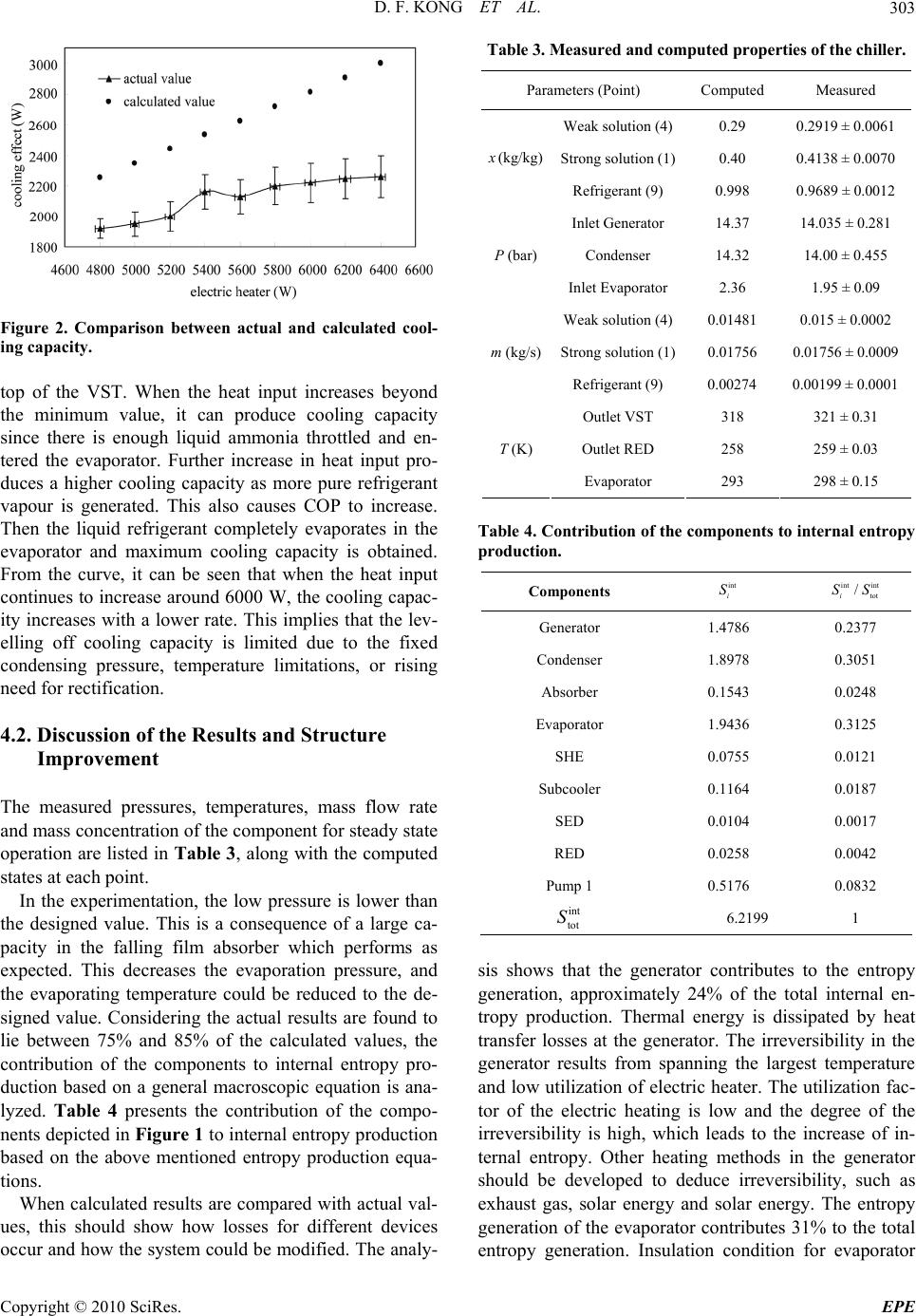 D. F. KONG ET AL. Copyright © 2010 SciRes. EPE 303 Figure 2. Comparison between actual and calculated cool- ing capacity. top of the VST. When the heat input increases beyond the minimum value, it can produce cooling capacity since there is enough liquid ammonia throttled and en- tered the evaporator. Further increase in heat input pro- duces a higher cooling capacity as more pure refrigerant vapour is generated. This also causes COP to increase. Then the liquid refrigerant completely evaporates in the evaporator and maximum cooling capacity is obtained. From the curve, it can be seen that when the heat input continues to increase around 6000 W, the cooling capac- ity increases with a lower rate. This implies that the lev- elling off cooling capacity is limited due to the fixed condensing pressure, temperature limitations, or rising need for rectification. 4.2. Discussion of the Results and Structure Improvement The measured pressures, temperatures, mass flow rate and mass concentration of the component for steady state operation are listed in Table 3, along with the computed states at each point. In the experimentation, the low pressure is lower than the designed value. This is a consequence of a large ca- pacity in the falling film absorber which performs as expected. This decreases the evaporation pressure, and the evaporating temperature could be reduced to the de- signed value. Considering the actual results are found to lie between 75% and 85% of the calculated values, the contribution of the components to internal entropy pro- duction based on a general macroscopic equation is ana- lyzed. Table 4 presents the contribution of the compo- nents depicted in Figure 1 to internal entropy production based on the above mentioned entropy production equa- tions. When calculated results are compared with actual val- ues, this should show how losses for different devices occur and how the system could be modified. The analy- Table 3. Measured and computed properties of the chiller. Parameters (Point) Computed Measured Weak solution (4)0.29 0.2919 ± 0.0061 Strong solution (1)0.40 0.4138 ± 0.0070 x (kg/kg) Refrigerant (9) 0.998 0.9689 ± 0.0012 Inlet Generator 14.37 14.035 ± 0.281 Condenser 14.32 14.00 ± 0.455 P (bar) Inlet Evaporator 2.36 1.95 ± 0.09 Weak solution (4)0.01481 0.015 ± 0.0002 Strong solution (1)0.01756 0.01756 ± 0.0009 m (kg/s) Refrigerant (9) 0.00274 0.00199 ± 0.0001 Outlet VST 318 321 ± 0.31 Outlet RED 258 259 ± 0.03 T (K) Evaporator 293 298 ± 0.15 Table 4. Contribution of the components to internal entropy production. Components int i S int int tot / i SS Generator 1.4786 0.2377 Condenser 1.8978 0.3051 Absorber 0.1543 0.0248 Evaporator 1.9436 0.3125 SHE 0.0755 0.0121 Subcooler 0.1164 0.0187 SED 0.0104 0.0017 RED 0.0258 0.0042 Pump 1 0.5176 0.0832 int tot S 6.2199 1 sis shows that the generator contributes to the entropy generation, approximately 24% of the total internal en- tropy production. Thermal energy is dissipated by heat transfer losses at the generator. The irreversibility in the generator results from spanning the largest temperature and low utilization of electric heater. The utilization fac- tor of the electric heating is low and the degree of the irreversibility is high, which leads to the increase of in- ternal entropy. Other heating methods in the generator should be developed to deduce irreversibility, such as exhaust gas, solar energy and solar energy. The entropy generation of the evaporator contributes 31% to the total entropy generation. Insulation condition for evaporator  D. F. KONG ET AL. Copyright © 2010 SciRes. EPE 304 may be improved to diminish irreversibility, to promote COP and cooling capacity. The entropy generation of the condenser contributes 30% to the total entropy generation. Counter-current condenser causes a larger temperature differences lead- ing to a bigger entropy generation, in spite of high heat transfer efficiency. When the thermodynamic state point remains in 10a instead of 10 with the subcooler before throttling, the cooling capacity is 9% more than the values without a subcooler. The entropy generation of the subcooler con- tributes 1.9% to the total entropy generation. It is con- cluded that, if the apparatus with a subcooler, the bene- fits outweigh its drawbacks. Simultaneous heat and mass transfer in the absorber contributes only about 2.5% to the internal entropy pro- duction of the chiller. The result also presents the con- tribution of the RED and SED on the chiller’s perform- ance, and it is only a significant, though not a dominating mechanism. 5. Conclusions A mathematical model is developed to analyze the per- formance of a single stage ammonia-water absorption refrigeration chiller with complete condensation. The apparatus is tested with heat input values between 4800 and 6400 W for a high pressure of 14 bar. The cooling capacity is found to be between 1900 and 2200 W with COP between 0.32 and 0.36. The actual results are found to lie between 75% and 85% of the calculated values. Comparisons between actual and calculated values show that heat loss from the generator have a remarkable effect on the system performance, and the cooling capac- ity is also limited due to fixed condensing pressure, tem- perature limitations, or rising efficiency for rectification. A more efficient thermal system should have a higher COP and a lower total entropy generation. The entropy generation is used to identify and quantify performance degradation and the components responsible for it. The results show that the larger irreversibility is caused by spanning the largest temperature and dissipated thermal energy by heat transfer losses at the generator and evapo- rator. 6. Acknowledgements An earlier version of this paper was presented at 2010 Asia-Pacific Power and Energy Engineering Conference. 7. References [1] F. Ziegler, “Recent Developments and Future Prospects of Sorption Heat Pump Systems,” International Journal of Thermal Sciences, Paris, Vol. 38, 1999, pp. 191-208. [2] A. Apte, “Ammonia Absorption Refrigeration Plants the Ideal Refrigeration System for New Millennium,” Trans- parent Energy Systems Private Limited, Pune, 2006. http://www. tespl.com [3] K. C. Ng, T. Y. Bong, H. T. Chua and H. L. Bao, “Theo- retical and Experimental Analysis of an Absorption Chiller,” International Journal of Refrigeration, London, Vol. 17, 1994, pp. 351-358. [4] A. Kececiler, H. I. Acar and A. Dogan, “Thermodynam- ics Analysis of Absorption Refrigeration System with Geothermal Energy: An Experimental Study,” Energy Conversion and Management, London, Vol. 41, 2000, pp. 37-48. [5] J. Chen and B. Andresen, “Optimal Analysis of Primary Performance Parameters for an Endoreversible Absorp- tion Heat Pumps,” Heat Recovery Systems and CHP, London, Vol. 15, 1995, pp. 723-731. [6] A. Bejan, J. V. C. Vargas and M. Solokov, “Optimal Allocation of a Heat Exchanger Inventory in Heat-Driven Refrigerators,” International Journal of Heat Mass Transfer, Vol. 38, No. 5, 1995, pp. 2997-3004. [7] N. E. Wijeysundera, “Analysis of the Ideal Absorption Cycle with External Heat-Transfer Irreversibilities,” En- ergy, London, Vol. 20, 1995, pp. 123-130. [8] C. Wu, “Cooling Capacity Optimization of a Waste Heat Absorption Refrigeration Cycle,” Heat Recovery Systems and CHP, Vol. 13, No. 4, 1993, pp. 161-166. [9] C. Wu, “Specific Heating Load of an Endoreversible Carnot Heat Pump,” International Journal of Ambient Energy, Vol. 14, 1993, pp. 25-28. [10] K. C. Ng, H. T. Chua and Q. Han, “On the Modeling of Absorption Chillers with External and Internal Irreversi- bilities,” Applied Thermal Engineering, Vol. 17, No. 5, 1997, pp. 413-425. [11] H. T. Chua, J. M. Gordon, K. C. Ng and Q. Han, “En- tropy Production Analysis and Experimental Confirma- tion of Absorption Systems,” International Journal of Refrigeration, Vol. 20, No. 3, 1997, pp. 179-190. [12] K. C. Ng, K. Tu and H. T. Chua et al., “Thermodynamic Analysis of Absorption Chillers: Internal Dissipation and Process Average Temperature,” Applied Thermal Engi- neering, Vol. 18, No. 8, 1998, pp. 671-682. [13] H. T. Chua, “Universal Thermodynamic Modeling of Chillers: Special Application to Adsorption Chillers,” Ph.D. Dissertation, National University of Singapore, Singapore, 1998. [14] H. T. Chua, H. K. Toh, A. Malek and K. C. Ng, K. Srini- vasan, “A General Thermodynamic Framework for Un- derstanding the Behavior of Absorption Chillers,” Inter- national Journal of Refrigeration, Vol. 23, No. 7, 2000, pp. 491-507. [15] H. T. Chua, H. K. Toh and K. C. Ng, “Thermodynamic Modeling of an Ammonia-Water Absorption Chiller,” International Journal of Refrigeration, Vol. 25, No. 7, 2002, pp. 896-906.  D. F. KONG ET AL. Copyright © 2010 SciRes. EPE 305 [16] “Thermo Physical Properties of Refrigerants,” ASHRAE Handbook, 2005. [17] R. Tillner-Roth and D. G. Friend, “A Helmholtz Free Energy Formulation of the Thermodynamic Properties of the Mixture {Water + Ammonia},” Journal of Physical and Chemical Reference Data, Vol. 27, No. 1, 1998, pp. 63-96. [18] K. C. Ng, H. T. Chua and K. Tu, “The Role of Internal Dissipation and Process Average Temperature in Chiller Performance and Diagnostics,” Journal of Applied Phys- ics, Vol. 83, No. 4, 1998, pp. 1831-1836. Nomenclature AFR Ammonia fluid reservoir COP Coefficient of performance h Specific enthalpy (kJ/kg) m Mass flow rate (kg/s) P Presser (bar) Q Heat transfer rate (W) RED Refrigerant expansion device s Specific entropy (kJ/kg•K) S Entropy production rate (W/K) SED Weak solution expansion device SFR Solution fluid reservoir SHE Solution heat exchanger T Temperature (K) VST Vertical sieve tray tower with complete con- densation W Work (kJ) x Ammonia mass concentration Subscripts a Absorber c Condenser e Evaporator g Generator i Component numbering index in Inlet conditions int Internal out Outlet conditions P Pump RED Refrigerant expansion device sc Subcooler SED Weak solution expansion device SHE Solution heat exchanger th Theoretical value Phase numbering index Superscripts tot Total value |

