Energy and Power En gi neering, 2010, 2, 262-270
doi:10.4236/epe.2010.24038 Published Online November 2010 (http://www.SciRP.org/journal/epe)
Novel Control Strategy for Multi-Level Active Power
Filter without Phase-Locked-Loop
Guojun Tan, Xuanqin Wu, Hao Li, Meng Liu
School of Information and Electrical Engineering, China University of Mining and Technology, Xuzhou, China
Received June 13, 2010; revised August 9, 2010; accepted September 21 , 20 1 0
Abstract
Active power filter (APF) using novel virtual line-flux-linkage oriented control strategy can not only realizes
no phase-locked-loop (PLL) control, but also achieves a good inhibitory effect to interfere. However, there
are some problems in the conventional method, such as the error of amplitude, the shift of phase angle and
the non-determinacy of initial oriented angle. In this paper, two one-order low-pass filters are adopted in-
stead of the pure integrator in the virtual line-flux-linkage observer, which can steady the phase and ampli-
tude. Furthermore, an original scheme of harmonics detection under the rotating coordinate is advanced
based on the simplified space vector pulse width modulation (SVPWM) strategy. Meanwhile, by using the
new SVPWM algorithm, the voltage space vector diagram of the three-level inverter can be simplified and
applied into that of two-level inverter, and this makes the control for Neutral Point potential easier.
Keywords: Active Power Filter, Harmonics Detection, Virtual Line-Flux-Linkage Observer, Active Power
Filter Control without Phase-Locked-Loop, Space Vector Pulse Width Modulation
1. Introduction
The use of nonlinear loads such as power electronic de-
vices leads to serious harmonics pollution and lager
voltage fluctuation. Moreover, lager unbalance voltage
and current distortions in the power system are harmful
to the electrical equipment and power systems. Shunt
active power filter (SAPF) can well compensate the har-
monic whose frequency and amplitude both changes, and
it is also recognized as an effective way to manage the
grid harmonic, to reactive power pollution and to im-
prove the quality of the power. Active power filter (APF)
is a new power electronics device for dynamic harmonics
restriction and reactive compensation without influenced
by system inductance [1,2], besides it has such functions:
adaptive ability for the parametric variation of system
and load, automatic tracing and compensation for the
varying harmonics [3,4]. There are some remarkable
advantages in nature of three-level APF, such as lower
distortion of output waveform, lower endure voltage and
less switch loss, high efficiency and low electromagnetic
interference (EMI), so it helps to raise the installed ca-
pacity and improves the harmonics compensation effect
as well as system reliability.
On the one hand, the traditional harmonic current de-
tection which is based on instantaneous reactive power
adopts phase-lock-loop (PLL) to acquire the voltage
vector angle [5-7], when the grid voltage fluctuation is
more serious, PLL will be in unlocked cond ition because
of the larger frequency offsets which can not accurately
track the phase position. To solve th e problem, th is paper
uses the virtual line-flux-linkage orientation to observe
the vector angle, which converts the observation of vec-
tor angle to the flux. By using the vo ltage integral on the
AC side of the active filter to estimate the grid flux, PLL
can be omitted; meanwhile, the power grid interference
can be inhibited well. On the other hand, the traditional
harmonic current detection requires that the integrated
vector combined by the sine and cosine function should
be synchronous and phase coincidence to the integrated
vector of the three-phase positive sequence fundamental
voltage, otherwise, the detection accuracy of the funda-
mental positive sequence reactive component will be
affected by phase difference [8]. Therefore, the harmonic
detection principle based on the rotating coordinates is
proposed in this paper. The application of virtual flux in
active filter system also includes controlling generation
of compensation cu rrent, so it has a very good control to
harmonic current detection and compensation current ge-

G. J. TAN ET AL.263
neration, and the voltage space vector modulation strat-
egy SVPWM (Space Vector Pulse Width Modulation)
can be easily applied to active filter co ntrol.
In this paper, the simplified three-level SVPWM with
neutral point potential ad aptive control is applied to con-
trol multi-level active filter, based on this, a n ovel multi-
level voltage active filter phase reconstruction algorithm
is proposed.
2. Mathematical Model for Thre e -Level APF
and the Rotating Coordinate Based
Harmonics Detection Diagram
Figure 1 is the main circuit of NPC three-level APF,
while vector diagram of the virtual line-flux-linkage ori-
ented system is shown in Figure 2. When the virtual
line-flux-linkage is at axis, then mathematical model
of three-level APF is in reference frame [9,10]:
ddq
Z
XAXBe
 (1)
where:


0
ssdd
ZdiagL LCC (2)
12
12
11
22
00
00
001
001
00110
Sdd
Sqq
dq
dq
LSS
LSS
ASS
SS










 





(3)
12
0T
d qdcdc
XiiVV

 (4)


11000Bdiag (5)
0
d
qm
e
eE




 (6)
In (2) to (6),
s
L
SS
: AC side inductance of APF; d: capacitance of
DC side; m: peak voltage of power system; : the
D-axis and Q-axis AC current of APF; 12dc dc VV: the
upper and down DC voltage relevant to neutral point;
112 2dqdq
: the D-axis and Q-axis components of
switching fu nction.
C
E
,S
,
dq
ii
,
,, S
According the virtual line-flux-linkage oriented strat-
egy showed in Figure 2, the reference compensation
current ca n b e obtained:
~
*
~
*
dh Ld
qh Lq
ii
ii





(7)
~
~
L
dLdLd
L
qLqLq
iii
iii







(8)
where:
,
L
dLq
ii: The D-axis and Q-axis current of nonlinear
load;
,
L
dLq
ii

: The D-axis and Q- axis funda mental current o f
nonlinear load through low pass filter from,
L
dLq
ii;
~~
,
L
dLq
ii: The D-axis and Q-axis component harmonics
current of nonl ine ar load.
3. The diagram of Novel Virtual
Line-Flux-Linkage Observer
The essence of virtual line-flux-linkage oriented method
is to gain accurate space angle (

) estimation of the ori-
ented vector


, as shown in Figure 2, the angle can be
obtained:
22
22
sin
cos













(9)
Then the estimation of

is converted to the evalua-
tion of

and

components of the virtual line-flux-
linkage.
di
eL v
dt
di
eL v
dt

















(10)
In (10), v

and v

are the

,

voltage quantity
at AC side of three-phase APF, respectively. Integrated
both sides of (10),
vdt Li
vdt Li












 (11)


,


:

,

value of virtual line-flux-linkage.
It can be seen from (11) that the flux linkage can be
evaluated by the voltage integral at AC side of APF,
while it brings a problem of the integral initial value
which cause an error of the flux linkage, furthermore, the
method of pure integrator doesn’t retrain the DC com-
ponent of the input signal, even a little DC component
can make the integrator saturation. In this manner, the
flux linkage in

 axes can be a circular trajectory
with DC offset corresponding to the centre of the circle,
meanwhile, it cause the inaccuracy of virtual line-flux-
linkage oriented angle and impact both the authenticity
of current feedback and the veracity of voltage space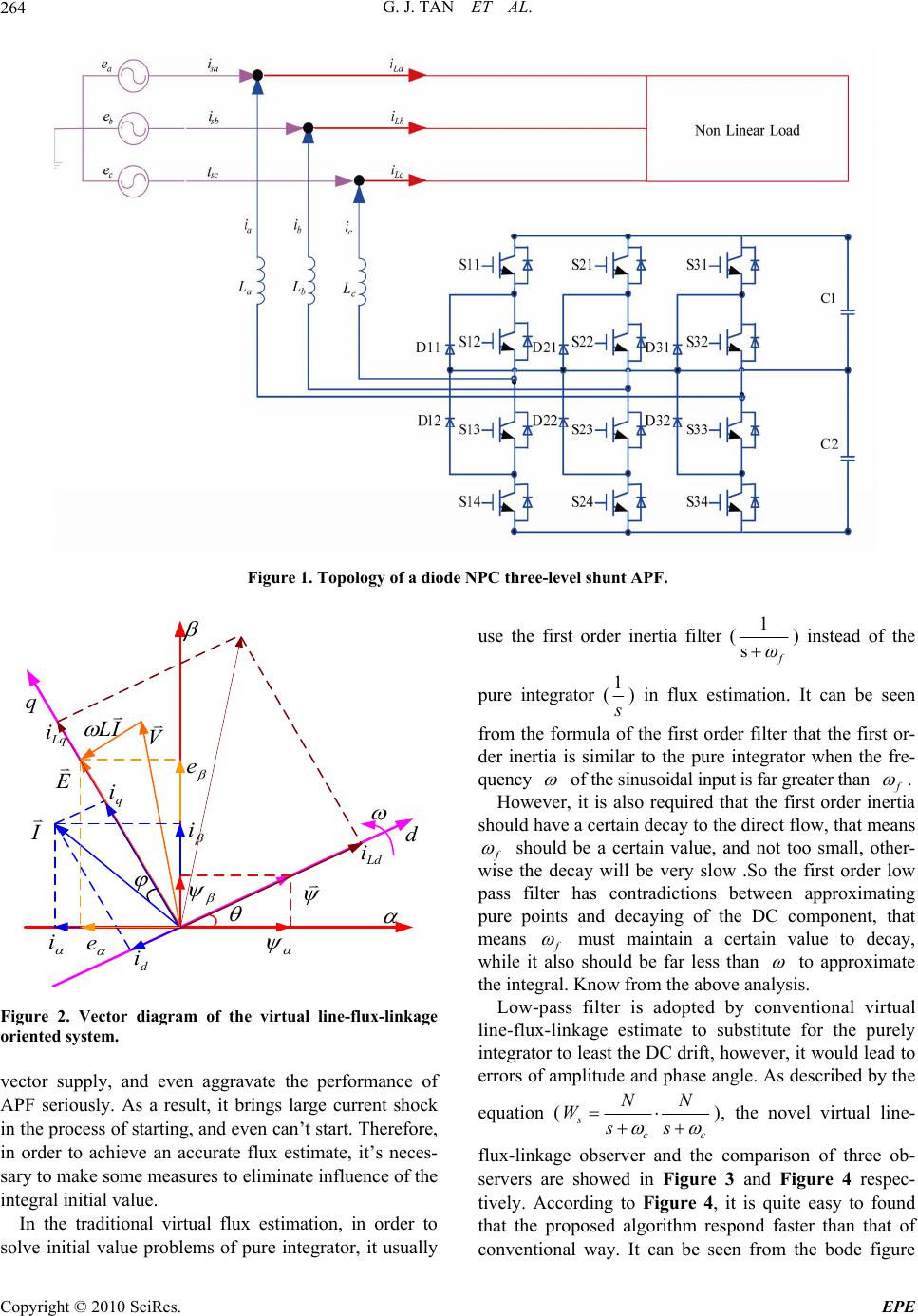

G. J. TAN ET AL. 264
Figure 1. Topology of a diode NPC three-level shunt APF.
1
s


d

q









e

i

e

i
E

V

I

IL 
q
i
d
i
Ld
i
Lq
i
Figure 2. Vector diagram of the virtual line-flux-linkage
oriented system.
nd even aggravate the performance of
PF seriously. As a result, it brings large current shock
blems of pure integrator, it usually
ter (use the first order inertia fil) instead of the
f


pure integrator (
vector supply, a
A
in the process of starting, and even can’t start. Therefore,
in order to achieve an accurate flux estimate, it’s neces-
sary to make some measures to eliminate influence of the
integral initial value.
In the traditional virtual flux estimation, in order to
solve initial value pro
1) in flux estimation. It can be seen
s
from the formula of the first orderthat the first or- filter
der inertia is similar to the pure integrator when the fre-
quency

of theinusoidal input is far greate r than s
f

.
Howevr, it is also required that the first order ia enerti
should have a certain decay to the direct flow, that means
f

should be a certain value, and not too small, other-
wise theecay will be very slow .So the first order low d
pa
mea
ss filter has contradictions between approximating
pure points and decaying of the DC component, that
ns
f

must maintain a certain value to decay,
while it also should be far less than

to approximate
the integral. Know from the above analysis.
Low-pass filter is adopted by conventional virtual
line-flunkage estimate to substitute for the purely
integrator to least th e DC drift, howev, it would lead to
errors of amplitude and phase angle. As desc
x-li er ribed by the
equation (scc
NN
Wss




), the novel virtual line-
flux-linkage observer and the comparison of three ob-
servers are showed in Figure 3 and Figure 4 respec-
tively. Acc, it is quite easy to found ording to Figure 4
that the proposed algorithm respond faster than that of conventional way. It can be seen from the bode figure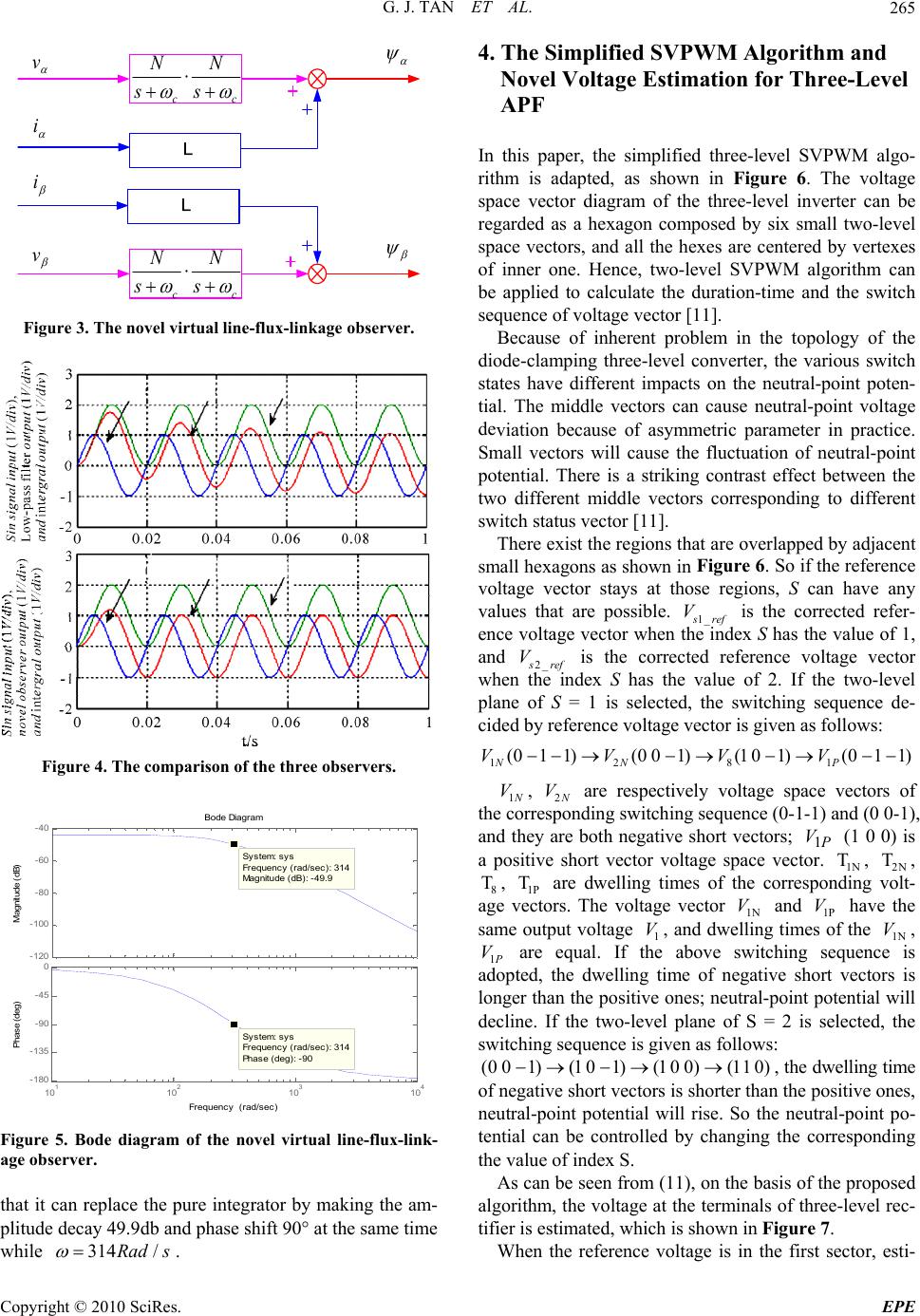

G. J. TAN ET AL.265

v

i


v

i



cc
s
N
s
N
 


cc
s
N
s
N
 


Figure 3. The novel virtual line-flux-linkage observer.
Figure 4. The comparison of the three observers.
Bode D i agram
F requency (rad/sec)
101102103104
-180
-135
-90
-45
0
System: sys
F requency (rad/sec): 314
Phase (deg): -90
Phase (deg)
-120
-100
-80
-60
-40
System: sys
F requency (rad/sec): 314
Magn itude (dB): -49.9
Magnitude (dB)
Figure 5. Bode diagram of the novel virtual line-flux-link-
age observer.
that it can replace the pure integrator by making the am-
plitude decay 49.9db and phase shift 90° at the same time
while 314/Rad s

.
4. The Simplified SVPWM Algorithm and
rit
sp tor diagram of the three-level inverter can be
garded as a hexagon composed by six small two-level
se neutral-point voltage
de
Novel Voltage Estimation for Three-Level
APF
In this paper, the simplified three-level SVPWM algo-
hm is adapted, as shown in Figure 6. The voltage
ace vec
re
space vectors, and all the hexes are centered by vertexes
of inner one. Hence, two-level SVPWM algorithm can
be applied to calculate the duration-time and the switch
sequence of voltage v ector [11].
Because of inherent problem in the topology of the
diode-clamping three-level converter, the various switch
states have different impacts on the neutral-point poten-
tial. The middle vectors can cau
viation because of asymmetric parameter in practice.
Small vectors will cause the fluctuation of neutral-point
potential. There is a striking contrast effect between the
two different middle vectors corresponding to different
switch status vector [11].
There exist the regions that are overlapped by adjacent
small hexagons as shown in Figure 6. So if the reference
voltage vector stays at those regions, S can have any
values that are possible. 1_
s
ref
V is the corrected refer-
ence voltage vector when the index S has the value of 1,
and 2_
s
ref
V is the corrected reference voltage vector
when the index S has the value of 2. If the two-level
plane of S = 1 is selectedswitching sequence de-
cided by reference voltage ve ctor is give n as follows:
1281
(0)(001)(10 1)(0 11)
NN P
VVVV
, the
1 1

 
1
N
V, 2
N
V are respectively voltage space vectors of
the corresponding switching sequence (0-1-1) and (0 0-1),
both negative short vectors; (1 0 0) is
voltage space
and they a
8, T
re
a positive short vector
are
P
V1
vector.
es o
1N 2N
1P dwelling times of the corresponding volt-
age vectors. The voltage vector 1N
V and 1P V have the
same output voltage 1
V, and dwelling timf the 1N V,
1
T, T,
T
P
V are equal. If the above switching senc
p the dwelling time of negative short vectors is
longer than the positive ones; neutral-point potential will
decline. If the two-level plane of S = 2 is selected, the
ching sequence is given as follows:
(001)(101)(100)(110)
quee is
ad
s
o te
wit
d,

 , the dwelling time
of negative short vectors is shorter than the positive ones,
neutral-point potential will rise. So the neutral-point po-
tential can be controlled by changing th
As can be seen from (11), on the basis of the proposed
algorithm, the voltage at the terminals of three-level rec-
e corresponding
the value of index S.
tifier is estimated, which is shown in Figure 7.
When the reference voltage is in the first sector, esti-

G. J. TAN ET AL. 266
Figure 6. The simplified th ree-level S VPWM algorithm.
Figure 7. The novel three-level voltage estimation algorithm.
mated three-phase voltages are given by:
11211
()
acalcdcdc aonboncon
uuuttt
 
33
333
11
)
33333
11211
cos(60 )()
33333
aon con
ccalcdcdc conaonbon
tt
uu uttt
 



 (15)
where, are the estimated voltage of
DC bus voltage of three-
are the duration-time of
three-phase for two-level algorithm, respectively.
Design and
Experimental Results Analysis
To verify the viability of proposed non PLL control
scheme for multi-level APF and evaluate performance of
this method, the test platform is established and operated,
and its control sketch is showed in Figure 9. As shown
in Figure 10, the structure of full-digital controller is
composed of DSP (TMS320F2812 of TI) and FPGA.
The system can implement DC bus voltage contro
5. The Main Circuit
l, har-
112
cos(60 )(
bcalc dcdc bon
uu ut
 



acalc
u,
three-level rectifier.
level rectifier.
bcalc
u,
aon
t,
ccalc
u
dc
u is
bon
t, tcon
Figure 8. Experiments waveform of the novel three-level
voltage estimation algorithm.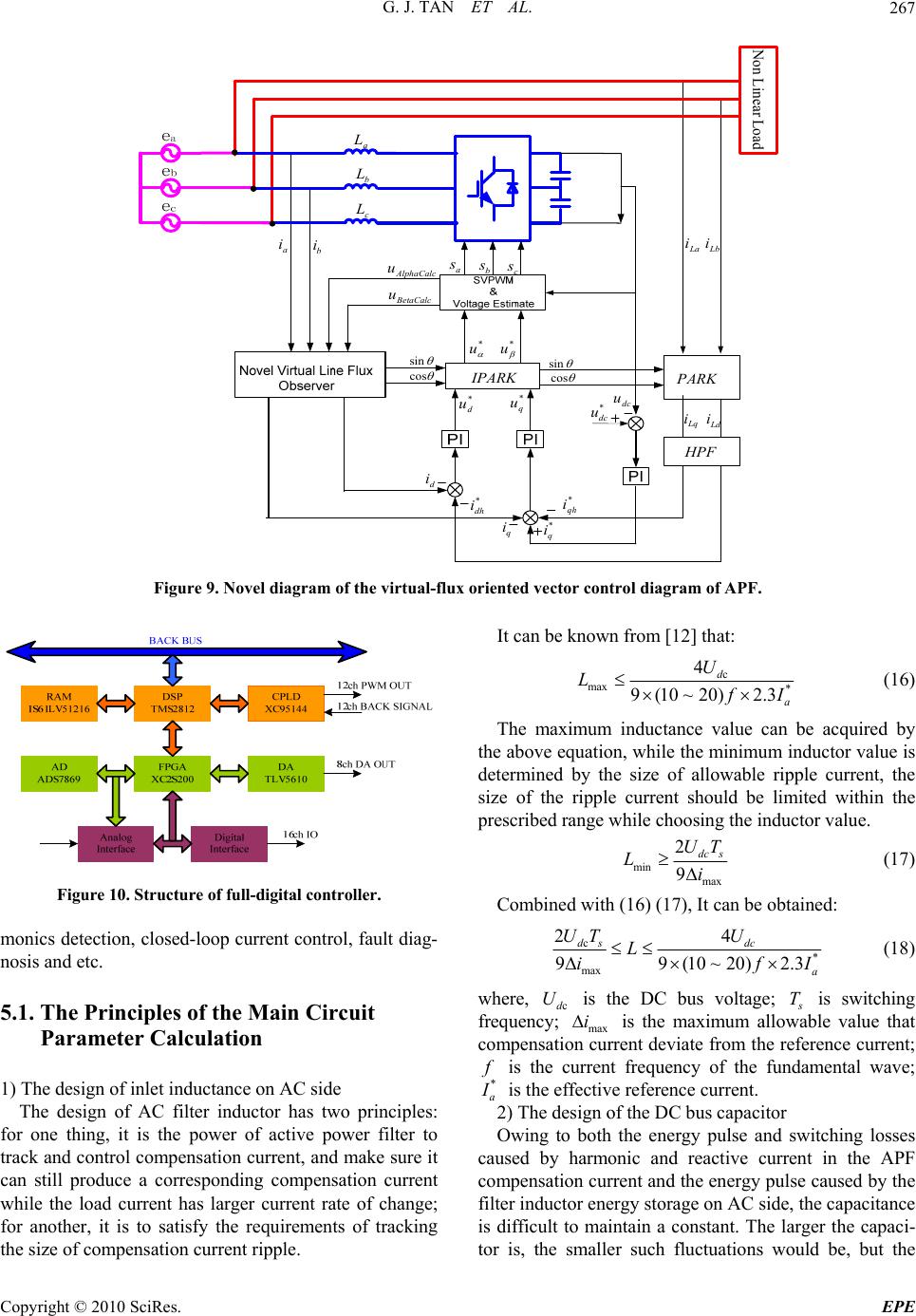

G. J. TAN ET AL.267
*
q
i
*
dh
i
d
i
q
i
*
dc
u
a
i
b
i
dc
u
*
d
u
*
q
u
*

u
*

u
a
s
b
s
c
s

sin

cos

sin

cos
*
qh
i
La
i
Lb
i
I
PARK
P
ARK
a
L
b
L
c
L
LoadLinear Non
Ld
i
Lq
i
HP
F
AlphaCalc
u
BetaCalc
u
Figure 9. Novel diagram of the virtual-flux oriented vector control diagram of APF.
Figure 10. Structure of full-digital controller.
monics detection, close
osis and etc.
5.1. The Principles of the Main Circuit
Parameter Calculation
1) The design of inlet inductance on AC side
The design of AC filter inductor has two principles:
for one thing, it is the power of active power filter to
track and control compensation current, and make sure it
can still produce a corresponding compensation current
while the load current has larger current rate of change;
for another, it is to satisfy the requirements of trackin
the size of compensation current ripple.
It can be known from [12] that:
d-loop current control, fault diag-
n
g
c
max *
4
9(10~20)2.3
d
a
U
LfI  (16)
The maximum inductance value can be acquired by
the above equation, while the minimum inductor value is
determined by the size of allowable ripple current, the
size of the ripple current should be limited within the
prescribed range while choosing the inductor value.
min max
2
9dc s
UT
Li  (17)
Combined with (16) (1 7), It can be obtained:
c
99(10 ~ 20)
ds dc
L
if


*
max
24
2.3 a
UT U
I
(18)
where, cd U is the DC bus voltage;
s
T is swi
cy; max itching equenfr

is the maximum allowable value that
compensation current deviate from the reference current;
f is the current frequency of the fundamental wave;
*
a
I
is the effective reference current.
osses
causecurrent in the APF
mpensation current and the energy pulse caused by the
apacitance
is difficult to maintain a constant. The larger the capaci-
tor is, the smaller such fluctuations would be, but the
2) The design of the DC bus capacitor
Owing to both the energy pulse and switching l
d by harmonic and reactive
co
filter inductor energy storage on AC side, the c

G. J. TAN ET AL. 268
capacitance value is not unlimited, so the design princi-
ples of DC bus capacitor is to work as a minimum ca-
pacitance while APF can be under normal operative con-
dition.
It can be known from [12] that:
min 2
c
ST
C (19)
c
(1) d
U


maxdc
dc
U
U



w
(20)
here, c
S is the compensating capacity of APF, T is
the control cycle of DC bus voltage, cd
U is the DC
voltage,

is the voltage wave pace, maxdc U is the
maximum allowable value of the voltage wave.
3) The controllable range of DC bus voltage
DC bus voltage selection should be considered as fol-
lows: it is not only necessary to
function, but also should not lead to too fierce current
chase APF
should be greater than the peak value of AC power grid
line voltage, that is
achieve a certain current
anges. The DC voltage threshold of three-ph
c3 dm
UE, otherwise,
can not be tracked. Take grid fluctuations and linear con-
e aer
be
the current
trol rangnd other factors into considation, the DC
voltage can c32
dm
E. Where, m E is the peak
value of the phase voltag e on AC side.
According to the above design principles, the main
cuit parameters of the APF test platf
U
cir orm are as follow:
ansformer: 380
V
d-side transformer is used to buck-boost in the
hi e effect caused by the
leakage reactance of transformer can
the non-linear load is of a large ca
portion harmonic. As can be seen in Figure 11, the
voltage distortion caused by tra
makes the phase-lock-loop in use
not n
ual flux orie
ux, the virtual-lin
er compensation,
th
tio low-pass
fil n
ux-linkage observer with two first-order low-pass
fil no 3, the
rientation angle and amplitude errors of the virtual flux
the novel
gorithm responses faster than traditional methods which
a) Power line voltage: 380 V/50 Hz, tr
/120 V, and system impedance is neglected;
b) Three-phase uncontrolled rectifier bridge is adopted
as the nonlinear load, its R = 8  inductance L = 1.5
mH;
c) Incoming inductance of APF: L = 1.7 mH, DC bus
voltage: d
U = 320 V, capacitance: C = 2300 uF.
5.2. The Experimental Results Analysis
The gri
gh-power applications system, thnot be ignored if
pacity or in high pro-
nsformer leakage reactance
unlocked condition thus it
can not accurately track the phase position which cad
the whole system shock. Thus, in the event that the
orientation angle is not exactly, APF can compensate
the harmonic of the nonlinear loads, on the cotrary, it
will cause system shock.
The virtual flux observer proposed in this paper uses
two first-order low-pass filters instead of pure integrator.
As the integral part has characteristics of a low-pass filter,
the amplitude of n times harmonic attenuate by n
times of fundamental when it comes through pure inte-
grator, which has some effect on filtering high harmonic,
that is to say, the virtnted has a good inhibi-
tion on the grid voltage distortion. It can be seen from
Figure 12, while using active filter control based on
novel virtual fl line-fluxkage switch
smoothly before and after net-side pow
e virtual flux angle can be able to accurately track the
phase position without the effect of grid voltage distor-
n.
The traditional virtual line-flux-linkage uses
ter instead of pure integrator which causes a certain
error of amplitude and phase agle, the new virtual
line-fl
ter instead of pure integral can be made no amplitude
error and phase shift. As can be seen in Figure 1
o
vector lead to higher current vector burr, and
al
makes the current vector stabilize rapidly.
a
i
a
e
PLL

)/5.4(
)/10()/60(
1
divsRadPL L
divAcurrentanddivVvoltageide

ofAngle
Grid
)/10(divmst
Figure 11. Control of the active filter based on phase-lock-
phase.
s
dc
u





)/25.1(
),/2.0(
),/100(
1divsRadlin kagefluxne
divweblinkagefluxlinertual
divVk

livirtua lofAngle
viofComponents
linDCofVolta ge
)/20(divmst
Figure 12. control of the active filter based on novel virtual
flux.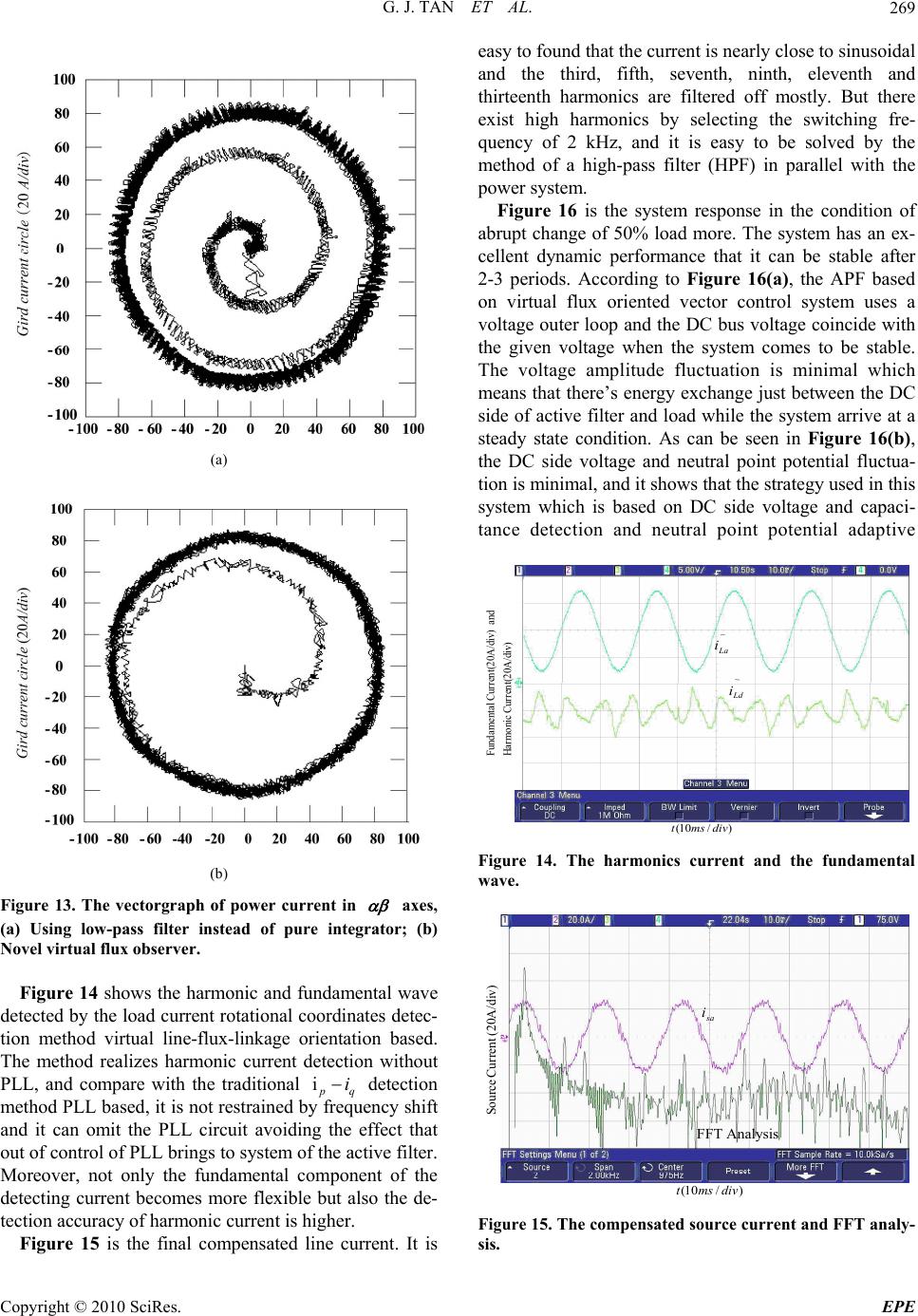

G. J. TAN ET AL.269
(a)
(b)
Figure 13. The vectorgraph of power current in


axes,
(a) Using low-pass filter instead of pure integrator; (b)
Novel virtual flux observer.
Figure 14 shows the harmonic and fundamental wave
detected by the load current rotational coordinates detec-
tion method virtual line-flux-linkage orientation based.
The method realizes harmonic current detection without
PLL, and compare with the traditional i
p
q
i
by freque
detection
method PLL based, it is not restrained ncy shift
and it can omit the PLL circuit avoiding the effect that
out of control of PLL brings to system of the active filter.
Moreover, not only the fundamental component of the
detecting current becomes more flexible but also the de-
tection accuracy of harmonic current is higher.
Figure 15 is the final compensated line current. It is
easy to found that the curre nearly close to sinusoidal
nd the third, fifth, seventh, ninth, eleventh and
thirteenth harmonics are filtered off mostly. But there
exist high harmonics by selecting the switching fre-
quency of 2 kHz, and it is easy to be solved by the
method of a high-pass filter (HPF) in parallel with the
power system.
Figure 16 is the system response in the condition of
abrupt change of 50% load more. The system has an ex-
cellent dynamic performance that it can be stable after
2-3 periods. According to Figure 16(a), the APF based
on virtual flux oriented vector control system uses a
voltage outer loop and the DC bus voltage coincide with
the given voltage when the system comes to be stable.
The voltage amplitude fluctuation is minimal which
means that there’s energy exchange just between the DC
side of active filter and load while the system arrive at a
steady state condition. As can be seen in Figure 16(b)
the DC side voltage and noint potential fluctua-
nt is
a
,
eutral p
tion is minimal, and it shows that the strategy used in this
system which is based on DC side voltage and capaci-
tance detection and neutral point potential adaptive

La
i
~
Ld
i
A/div)C urrent(20 Harmonic
and A/div)Current(20 lFundamenta
)/10(divmst
Figure 14. The harmonics current and the fundamental
wave.
sa
i
Analysis FFT
(20Current Source
)/10(divmst
Figure 15. The compensated source current and FFT analy-
sis.
A/div)

G. J. TAN ET AL. 270
dc
u
/div)
an
sa
i
(10A Currents Source
d
div )200V/lin DC of Voltages
)/50(divmst
(a)
k(
updc
u
_
downdc
u
_
intneutral_po
u
(50/divint
div)0V/
)po ne utr al of Volt age s
andli DC of Voltages
)/50(divmst
(b)
Figure 16. The dynamic response of the system, (a) The
power system current and DC bus voltage response under
abrupt condition; (b) DC bus voltage and neutral point
potential response under abrupt c ondition.
hese results proved that the novel control algorithm
with virtual line-flux-linkage-oriented based control sys-
tem possess strong robustness, and also demonstrated
that the simplified three-level SVPWM strategy with
neutral point potential self-adaptation is valid.
6. Conclusions
The experimental results show that the scheme of adopt-
ing the proposed virtual line-flux-linkage-oriented ob-
server can realize the non-PLL control for APF, and dis-
played that the load current detection under rotatin
ordinate oriented by virtual line-flux-linkage can n
only detects harmonics cut rapidly but also makes
e compensating current tracked reference fast, and in-
dicated that APF system with the method of discusse
flux oriented and rotating coordinate based harmonics
detection has the characteristics of decreasing line total
harmonic distortion (THD) significantly and superior
dynamic property, thus it is obvious that leading the sim-
plified three-level SVPWM strategy with neutral point
potential self-adaptation in control can improve the sys-
tem’s overall performance.
7. References
[1] M. EI-Habouk, M. K Darwish and P. Mehta, “Active
Power Fliter. A Review,” IEE Proceedings of Electron
Power Application, Vol. 147, No. 7, January 2000, pp.
403-414.
[2] M. Izhar and C. M. Hr, “Performance for Passive
rque Control of
ng. “A 31-
s,” IEEE
Industrial Electrics, Vol. 49, No. 3, June
] L. S. Czarnecki, “On Some Misinterpretation of the In-
da “A New Method to Elimate
urrents by Magnetic Flux Compensation
on Basic Design,” IEEE Transactions on
, Vol. PAS-90, No. 5, Septem-
adze
Filter Inreducing Harmonics in the Distribution System,”
Power and Energy Conference, Selangor, November
2004, pp. 104-108.
[3] M. Jasinski, D. Swierczynski and M. P. Kazmierkowski,
“Novel Sensorless Direct Power and To
Space Vector Modulated ac/dc/ac Converter,” IEEE In-
ternational Symposium, Vol. 2, May 2004, pp.
1147-1152 .
nk(10
[4] Y. Ye, M. Kazerani, V. H. Quintana, “A Novel Modeling
and Control Method for Three-Phase PWM Converters,”
IEEE 32th Annual, PESC, Vancouver, Vol. 1, June 2001,
pp. 102-107.
[5] C. K. Lee, S. Y. Ron Hui and H. S.-H. Chu
Level Casecade Inverter for Power Application
Transactions on
2002, pp. 613-617.
[6 stantaneous Reactive Power p-q Theory,” IEEE Transac-
tions on PE, Vol. 19, No. 3, May 2004, pp. 828-836.
[7] M. Malinowski, M. P. Kazmerkowski, S. Hansen,
FBlaabjerg and C. D. Marques,“Virtual-Flux-Based Di-
rect Power Control of Three-phase PWM Rectifiers,”
IEEE Transactions on Industry Applications, Vol. 37, No.
4, August 2001, pp. 1019-1027.
[8] H. Sasaki and T. Machida “A New Method to Elimate
AC Harmonic Currents by Magnetic Flux Compensation
Considerations on Basic Design,” IEEE Transactions on
Power Application System, Vol. 90, No. 5, 1971, pp.
2009-2019
[9] R. D. Zhao and Y. K. He, “Simulation Study on the Vir-
tual Line Flux Oriented Vector Control of the PWM Rec-
tifier,” Proceedings of the CSU 2EPSA, Vol. 17, No. 5,
October 2005, pp. 94-98.
10] H. Sasaki and T. Machi
compensation can effectively control the neutral-poin
potential both in static and dynamic operating conditions.
T
t
[
g co-
o
ber 1971, pp. 2009-2019.
[11] J. H. Seo, C. H. Choi and D. S. Hyun, “A New Simplified
Space-Vector PWM Method for Three-Level Inverter,”
IEEE Transactions on Power Electronics, Vol. 16, No. 4,
AC Harmonic C
Considerations
Power Application System
t
rren
th d
July 2001, pp. 545-550.
[12] E. Teresa and J. A. Pomilio, “Shunt Active Power Filter
Synthesizing Resistive Load,” IEEE transactions on
Power Electron, Vol. 17, No. 2, March 2002, pp. 273-278.