Paper Menu >>
Journal Menu >>
 Energy and Power En gi neering, 2010, 2, 248-253 doi:10.4236/epe.2010.24036 Published Online November 2010 (http://www.SciRP.org/journal/epe) Copyright © 2010 SciRes. EPE Numerical Simulation of Water Droplets Deposition on the Last-Stage Stationary Blade of Steam Turbine Danmei Xie, Xinggang Yu, Wangfan Li, Youmin Hou, Yang Shi, Sun Cai School of Power and Mechanical Engineering, Wuhan University, Wuhan, China E-mail: dmxie@whu.edu.cn, lwf1988725@163.com Received June 29, 2010; revised August 10, 2010; accepted September 17, 2010 Abstract Based on the method of discrete phase, the law of droplets’ deposition in the last stage stationary blade of a supercritical 600 MW Steam Turbine is simulated in the first place of this paper by using the Wet-steam model in commercial software FLUENT, where the influence of inlet angle of water droplets of the station- ary blades is also considered. Through the calculation, the relationship between the deposition and the di- ameter of water droplets is revealed. Then, the amount of droplets deposition in the suction and pressure sur- face is derived. The result is compared with experimental data and it proves that the numerical simulation result obtained in this paper is reasonable. Finally, a formula of the relationship between the diameter of wa- ter droplets and the inlet angle is fit, which could be used for approximate calculation in the engineering ap- plications. Keywords: Stea m Turbine, Stationary Blade, Wet Steam, Water Droplets Deposition, Discrete Phase, Numerical Simulation 1. Introduction In the energy industry, high efficiency steam turbine is widely used as a driving machine and its dominant posi- tion in the power industry will stay for a long time. For the last stage of steam turbine in the th ermal power plant and nuclear station, steam will spontaneously condensate and generate a large number of tiny water droplets, called the primary water droplets with the diameter of about 0.01-2.0 μm, when it expands to wet steam zone in the cascade channel. The amount of primary water drop- lets accounts for nearly 90% of the liquid mass in wet steam [1]. The remainder part will form water film or stream of steam, due to inertia and turbulent diffusion deposition on the blade surface, wh ich will be brought to the trailing edge by the steam and split out to form sec- ondary water droplets under action of pulling force of steam. Compared with the primary water droplets, the number of the secondary water droplets is smaller and the diameter is larger (less than 200 μm), but the mass of a single droplet is larger. It is difficult to speed up the flow speed. Severe erosion will b e caused on the moving blade when it impacts the surface of moving blade with a high relative velocity. For the steam turbine running in the wet steam turbine area, such erosion is obvious and it threatens the safe operation [2]. Moreover, according to Baumann moisture loss formula, 1% of the moisture produces 1% of loss [3], it can be seen that this erosion will reduce the efficiency of units. It is necessary to study the law of droplets deposition on the blades of the final stage of the steam turbine. At present, the numerical simulation result of the droplets deposition on the channel of stationary blades of steam turbine differ greatly from that obtained with the experimental data [4-6]. That is because most of the cal- culations are based on such assumptions as the direction of flow is parallel to the blade setting angle, and the in- fluence of inlet angle for water droplets to the d eposition amount and location of deposition is ignored, when the discrete phase model is used to calculate the droplets deposition. By considering the influence of inlet angle of water droplets of the stationary blade, this paper studies the relationship between the deposition and the diameter of water droplets and the amount of droplets deposition in the suction and pressure surface. 2. Steam Control State Equations Generally, the three physics laws of conservation, namely: mass conservation law, momentum conservation law and  D. M. XIE ET AL. Copyright © 2010 SciRes. EPE 249 energy conservation law, must be followed in fluid cal- culations. According to the characteristics and nature of the flow, other constraint equations should be included, such as: viscosity transport equation, fraction conserva- tion equation, etc. 2.1. Mass Conservation Equation (Continuity Equation) im i uS tx (1) The equation is suitable to either compressible flows or incompressible flows. Source Sm is the mass trans- ferred from the dispersed secondary phase to continuous phase (for example, mass caused by the liquid evapora- tion), the source term can also be the source defined by customer. 2.2. Momentum Conservation Equation The momentum conservation equation in the direction of i of the inertial (non-accelerating) coordinate system is: ij iij ii jij p uuu gF tx xx (2) where ρ is the static pressure, τij is the stress tensor, ρgi and Fi are the gravitational body force and external body forces of the i direction, such as the lift force due to in- teraction of the discrete phase. Fi includes other relevant source terms, such as porous medium and customer de- fined source term. 2.3. Energy Conservation Equation () () () () ()()() T ppp TuTvTwT txy z kTkTkT S xc xyc yzc z (3) where ρ is fluid density, t is time. u, v, w is the velocity component in x, y, z axis of fluid infinitesimal vector u. T is temperature, k is the heat transfer coefficient for the fluid, cp is specific heat capacity of fluid, ST is the inner heat source for the fluid. 2.4. State Equation Virial state equation [7] is used as the steam state equa- tion use. 3 g 2 ggg 1 DCBRTP (4) where ρg is the density, T is temperature, P is pressure. B, C and D are the first, the second and the third order virial coefficients respectively. Above Equations (1)-(4) co nstitute closed equ ations of solution to the problem. If two-phase flow is investig ated, the impact of particles on the continuous phase formula should be added to the above equations. 3. Calculation Model and Boundary Condition 3.1. Calculation Model and Structure The physical dimensions in the cross section of 73% height of a 600 MW steam turbine stationary blade are used referr ed in physical modeling in this paper. Becau se that the internal flow of steam turbine is within limited space in irregular regions and its solution is within that area both for contraction and expansion conditions, non- uniform mesh are used in meshing and the mesh spacing are adjusted according to speed and pressure gradient and liquid phase deposition in this paper, to ensure that each part of the node spacing is relatively stable. The wall of blade is the place to where droplets are attached. The blade trailing edge is the zone where the secondary droplet is formed when water film is torn due to steam separation. Intensive energy exchange occurs in the blade trailing edge with severe turbulence and pressure fluctuation. So refining meshing is applied in these two regions. Figure 1 shows the final computing mesh in this paper. 3.2. Boundary Condition Inlet and outlet boundary conditions are set as pressure inlet and pressure outlet, the blade wall is treated as no slip wall, and the upper and lower boundary is set as pe- riodic boundary conditions. The design parameters of a Figure 1. Two-dimensional grid of stationary blade.  D. M. XIE ET AL. Copyright © 2010 SciRes. EPE 250 600 MW steam turbine are listed as followings: mean total pressure of inlet is 18793.76 Pa; mean total tem- perature of outlet is 330.96 K; mean back pressure of outlet is 11924.83 Pa; outlet pressure of inner hollow stationary blade is 9200Pa; inlet humidity of wet steam is 0.0794, outlet humidity is 0.083. In this paper, wet-steam module in multi-phase is used, and some user-defined function code is compiled. The Realizable k-ε turbulence model is selected from turbu- lence equations, SIMPLE algorithm is set for the pres- sure and velocity coupling, and second order upwind scheme are used for discrete equations. 3.3. The Relationship between the Inlet Angle of Droplets and the Diameter of Droplets The literature [8] showed th at the depositio n water on the surface of last stage stationary blade follows such law as: most water on the surface of stationary blade is from inert deposition of second ary water droplets, and the dis- tribution of secondary water droplets with different size is related to the circumferential speed of the secondary last moving blade. As the speed and direction of secon- dary water droplets into the flow of stationary blade are greatly related with the circumferential speed of secon- dary last moving bucket, the axial clearance and the steam flow. In general, the larger the circumference speed or the smaller the axial clearance, the larger the inlet angle of droplets when sprayed into the stationary blade. The direction of secondary water droplets with about 10 µm diameter into the statio nary b lad e chan n el is basically close to the inlet angle of steam. The water droplets of the level of average diameter of about 20-25 μm will enter the stationary blade channel with angle slightly greater than 90 °. As for water droplets of 40 μm, due to a great inertia force, will flow into the channel with large negative incidence angle. Droplets of larger diameter will be directly thrown to outer edge or dia- phragm owing to small proportion of the total droplets’ mass or great inertia force. Therefore, the impact of lar- ger diameter of the droplets in the stationary blade can be basically negligible. Based on the above analysis, the diameter of partial droplets and their corresponding proportion of mass as well as the entry angle needed for the numerical simula- tion are calculated and collected. Here α is taken as the supplementary angle of inlet angle. Some data is shown in Table 1. 4. Parameter Setting of Discre te Phase In this paper, the discrete phase model (DPM) is used to investigate the movement of water droplets in the last stage of stationary blade and the impact of water droplets to the vapor phase flow field. In FLUENT, the discrete phase model is applied by defining the initial position, the speed, the size and the temperature of particles. Ini- tial condition of particles defined by the physical prop- erty of particle can be used to initialize the trajectory of particles and heat and mass transfer calculations. In this paper, the injection type is group injection, and the particle type is inert. 1000 particle streams are de- fined in this calculation [9]. In this paper, a distribution method called Rosin- Rammler is employed to define the distribution of parti- cle size. In this way, the overall range of particle size is divided into discrete size groups, while each size group is represented by a single particle stream of group injec- tion. For Rosin-Rammler distribution, it’s assumed that there is an exponential relationship between the particle diameter d and the mass fraction Yd of particles whose diameter is larger than d, as: (/) n dd d Ye (5) where d is the mean diameter (average diameter), n is the spread pa r ameter. Figure 2 shows the droplets size distribution and Table 1. Data of diameter of droplets, proportion of mass and inlet angle. Diameter of Droplets D/μm Proportion of Mass Q Entry Angle α/º 2 0.00066 88 7 0.0102 82 12 0.02878 78 17 0.04638 73 21 0.05101 70 25 0.04417 67 30 0.02601 62 35 0.010058 57 40 0.002437 53 Figure 2. The diameter of droplets and the curve of mass distribution [9]. 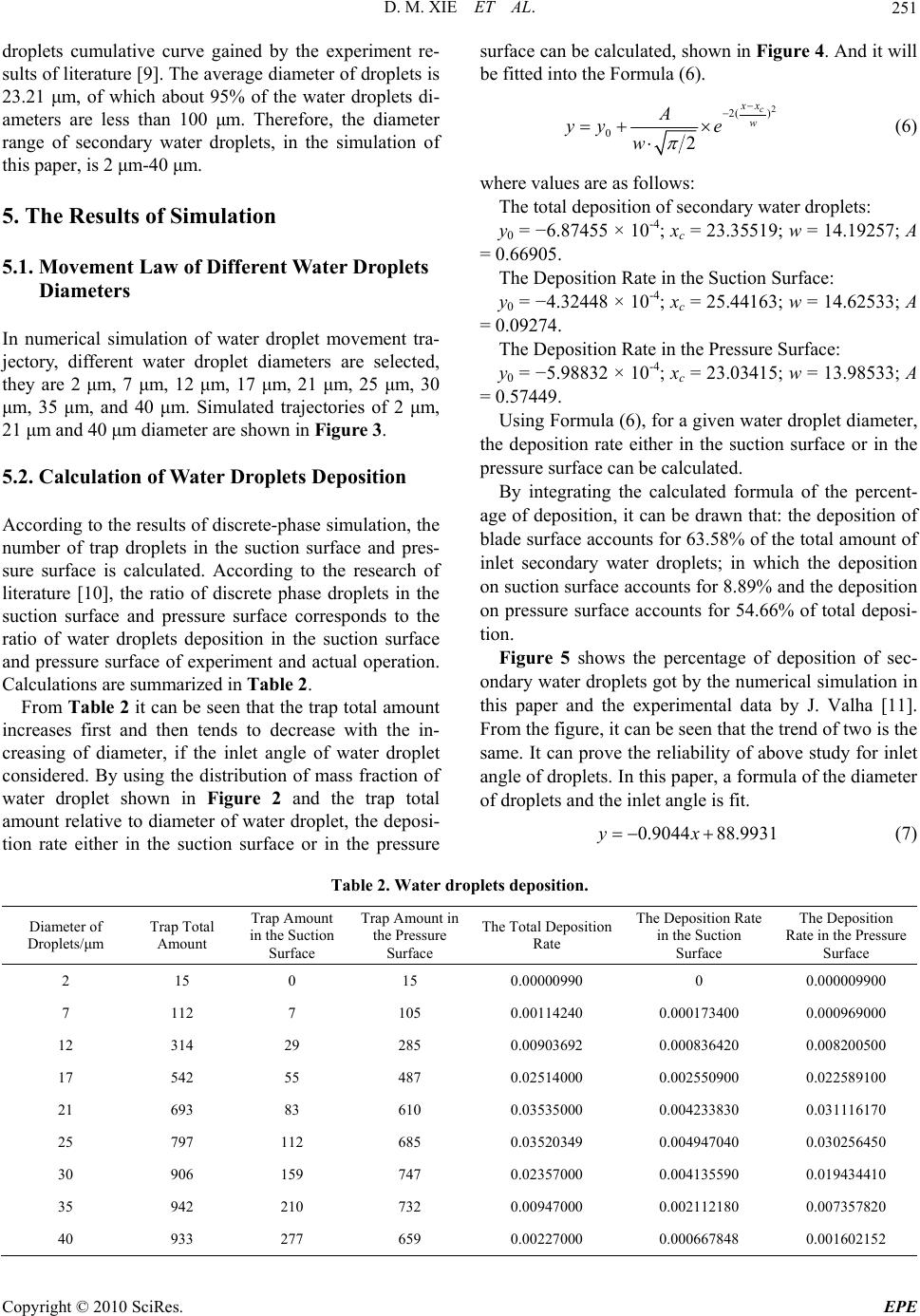 D. M. XIE ET AL. Copyright © 2010 SciRes. EPE 251 droplets cumulative curve gained by the experiment re- sults of literature [9]. The averag e diameter of droplets is 23.21 μm, of which about 95% of the water droplets di- ameters are less than 100 μm. Therefore, the diameter range of secondary water droplets, in the simulation of this paper, is 2 μm-40 μm. 5. The Results of Simulation 5.1. Movement Law of Different Water Droplets Diameters In numerical simulation of water droplet movement tra- jectory, different water droplet diameters are selected, they are 2 μm, 7 μm, 12 μm, 17 μm, 21 μm, 25 μm, 30 μm, 35 μm, and 40 μm. Simulated trajectories of 2 μm, 21 μm and 40 μm diameter are shown in Figure 3. 5.2. Calculation of Water Droplets Deposition According to the results of discrete-phase simulation, the number of trap droplets in the suction surface and pres- sure surface is calculated. According to the research of literature [10], the ratio of discrete phase droplets in the suction surface and pressure surface corresponds to the ratio of water droplets deposition in the suction surface and pressure surface of experiment and actual operation. Calculations are summarized in Table 2. From Ta ble 2 it can be seen that the trap total amount increases first and then tends to decrease with the in- creasing of diameter, if the inlet angle of water droplet considered. By using the distribution of mass fraction of water droplet shown in Figure 2 and the trap total amount relative to diameter of water droplet, the deposi- tion rate either in the suction surface or in the pressure surface can be calculated, shown in Figure 4. And it will be fitted into the Formula (6). 2 2( ) 02 c xx w A yy e w (6) where values are as follows: The total deposition of secondary water droplets: y0 = −6 .87455 × 10-4; xc = 23.35519; w = 14.19257; A = 0.66905. The Deposition Rate in the Suction Surface: y0 = −4.32448 × 1 0-4; xc = 25.44163; w = 14.62533; A = 0.09274. The Deposition Rate in the Pressure Surface: y0 = −5.98832 × 1 0-4; xc = 23.03415; w = 13.98533; A = 0.57449. Using Formula (6), for a given water droplet diameter, the deposition rate either in the suction surface or in the pressure surface can be calculated. By integrating the calculated formula of the percent- age of deposition, it can be drawn that: the deposition of blade surface accounts for 63.58% of the total amount of inlet secondary water droplets; in which the deposition on suction surface accounts for 8.89% and the deposition on pressure surface accounts for 54.66% of total deposi- tion. Figure 5 shows the percentage of deposition of sec- ondary water droplets got by the numerical simulation in this paper and the experimental data by J. Valha [11]. From the figure, it can be seen that th e trend of two is the same. It can prove the reliability of above study for inlet angle of droplets. In this paper, a formula of the diameter of droplets and the inlet angle is fit. 0.9044 88.9931yx (7) Table 2. Water droplets deposition. Diameter of Droplets/μm Trap Total Amount Trap Amount in the Suction Surface Trap Amount in the Pressure Surface The Total Deposition Rate The Deposition Rate in the Suction Surface The Deposition Rate in the Pressure Surface 2 15 0 15 0.00000990 0 0.000009900 7 112 7 105 0.00114240 0.000173400 0.000969000 12 314 29 285 0.00903692 0.000836420 0.008200500 17 542 55 487 0.02514000 0.002550900 0.022589100 21 693 83 610 0.03535000 0.004233830 0.031116170 25 797 112 685 0.03520349 0.004947040 0.030256450 30 906 159 747 0.02357000 0.004135590 0.019434410 35 942 210 732 0.00947000 0.002112180 0.007357820 40 933 277 659 0.00227000 0.000667848 0.001602152  D. M. XIE ET AL. Copyright © 2010 SciRes. EPE 252 (a) (b) (c) Figure 3. Water droplets trajectory of each diameter. (a) water droplets trajectory of diameter of 2 μm; (b) water droplets trajectory of diameter of 21 μm; (c) water droplets trajectory of diameter of 40 μm.  D. M. XIE ET AL. Copyright © 2010 SciRes. EPE 253 Figure 4. The percentage of water droplets deposition. Figure 5. The ratio of secondary water droplets of experi- ment data [11]. where x is the diameter of droplet. Using Formula (7), for a given water droplet diameter, the deposition rate of second water droplet on each sur- face can be calculated. It can be easily used in approxi- mate engineering calculations of inlet angle in the last stage of stationary blade of steam turbine. 6. Conclusions Taking a last stage stationary blade of a supercritical 600 MW steam turbine as an object, droplets with different diameter are selected to simulate the movement trajec- tory of particles, and the influence of the inlet angle of water droplets changing with the droplets diameter are taken into account. By simulating calculation, a formula of the diameter of droplets and the inlet angle is fit and a curve of water droplets deposition is drawn according to the formula. compared the curve with the experimental data, it can be found out that the tendency of results by the two methods are same. Furthermore, the relationship between the di- ameter of water droplets and inlet angle is fit as a for- mula in the paper, which can be used for approximate calculation in the engineering application. 7. References [1] Z. P. Feng, L. Li and G. J. Li, “The Status and Progress of Numerical Study on Two-Phase Condensate Flows of Steam Turbine,” Shanghai, 2002, pp. 1-10. [2] Y. M. Hou, “Optimization Design of New Type Hollow Stationary Dehumidity Blade in the Last Stage of SC Steam Turbine,” Wuhan University, Wuhan, 2010. [3] M. J. Moore and C. H. Sieverding, “Low Pressure Tur- bine and the Condenser Aerothermodynamics,” Z. M. Weng, M. Z. Yu, D. J. Cheng and B. Liu Translate, Xi’an Jiaotong University Press, Xi’an, Vol. 66, 1992. [4] S. A. Slater, A. D. Lee Ming and J. B. Young, “Particle Deposition from Two Dimensional Turbulent Gas Flows,” International Journal of Multiphase Flow, Vol. 29, No. 5, 2003, pp. 721-750. [5] C. G. Li, X. J. Wang, et al., “Numerical Investigation of Movement and Deposition of Water Droplets on Steam Turbine Stationary Cascade,” Power Engineering, Vol. 42, No. 9, 2008, pp. 22-26. [6] Y. F. Zhao, Y. Z. Wang, Y. F. Liu and B. Sun, “Removal Method of Depositional Droplets and Energy Analysis in Hollow Cascade,” Power Engineering, Vol. 24, No. 3, 2004, pp. 515-519. [7] L. Li, Z. P. Feng and G. J. Li, “Numerical Simulation of Wet Steam Flow with Spontaneous Condensation in Tur- bine Cascade,” Journal of Engineering Thermophysics, Vol. 23, No. 3, 2002, pp. 309-311. [8] M. Z. Yu and Y. Huang, “Dewetting Method and Deposi- tion Law of Steam Turbine at the Last Stage,” Turbine Technology, Vol. 5, 1988, pp. 44-50. [9] X. J. Wang, C. Lu, J. C. Liu, et al. “Slot Location of the Hollow Stationary Blade to Water Performance Test,” Engineering for Thermal Energy and Power, Vol. 22, No. 5, 2007, pp. 12-15. [10] S. Cai, D. M. Xie, et al. “Numerical Simulation of Suc- tion Slot Structure on the LP Last Stage Stationary Blades of Steam Turbine,” Asia-Pacific Power and Energy En- gineering Conference, Chengdu, 2010. [11] J Valha, “Liquid Phase Movement in the Last Stages of Large Condensing Steam Turbines,” Proceedings of the Institution of Mechanical Engineers, Conference Pro- ceedings 1964-1970, Vol. 178-184. |

