Energy and Power Engineering, 2010, 2, 213-222
doi:10.4236/epe.2010.24032 Published Online November 2010 (http://www.SciRP.org/journal/epe)
Multi-Deployment of Dispersed Power Sources Using
RBF Neural Network
Yaser Soliman Qudaih, Takashi Hiyama
Computer Science and Electrical Engineering Department, Kumamoto University,
Kumamoto, Japan
Received June 16, 2010; revised August 2, 2010; accepted September 6, 2010
Abstract
Multi-deployment of dispersed power sources became an important need with the rapid increase of the Dis-
tributed generation (DG) technology and smart grid applications. This paper proposes a computational tool to
assess the optimal DG size and deployment for more than one unit, taking the minimum losses and voltage
profile as objective functions. A technique called radial basis function (RBF) neural network has been util-
ized for such target. The method is only depending on the training process; so it is simple in terms of algo-
rithm and structure and it has fast computational speed and high accuracy; therefore it is flexible and reliable
to be tested in different target scenarios. The proposed method is designed to find the best solution of multi-
DG sizing and deployment in 33-bus IEEE distribution system and create the suitable topology of the system
in the presence of DG. Some important results for DG deployment and discussion are involved to show the
effectiveness of our proposed method.
Keywords: Dispersed Power Sources Deployment, RBF Neural Network, Power Losses Reduction
1. Introduction
The optimal deployment of the dispersed power sources
has been discussed as an important factor related to the
effect of the DG penetration [1-3]. Keane and O’Malley
explain the background to the technical constrains faced
by DG projects using linear programming method to
determine the optimal allocation [1]. Almost the same
approach has been analytically discussed to find the
proper size and allocation of DG unit to reduce power
losses of the distribution networks [2,3]. On the other
hand, Nara et al. have already presented that the distribu-
tion system losses can be further reduced if DGs are op-
timally allocated on demand side of distribution system
using Tabu search algorithm [4]. The same objective to
find the power loss reduction of distribution feeder using
parametric formula was proposed as in [5]. The extended
efforts of this topic come from Kashem et al. where they
intend to prove that the appropriate size and location of
DG play a significant role in minimizing power losses in
distribution systems by introduction of sensitivity analy-
sis [6]. Other researchers like Le et al. and Durga et al.
point this problem from different views. The first group
discusses the matter of DG size and allocation taking
economic aspects into consideration using sequential
quadratic programming (SQP) algorithm [7]. Meanwhile,
Durga and Mithulananthan consider the DG existence in
the corridor of deregulated electricity market [8]. How-
ever, all of the above mentioned efforts tried to solve the
DG size and allocation problems based on analytical
method and only able to provide a single solution for
their objective studies. The general approach to provide
the optimal results using such kind of optimization tech-
niques is by iteration process. If the step time is small,
the result is highly accurate but slowing the computa-
tional time. Conversely, if the step time is big, the com-
putational time is fast but the result is less accurate.
Therefore, the analytical method will end up with high
computational burden, time-consuming and less flexible
for different objective functions.
The discussion about the existence of DG units is
broadened to different aspects, such as reliability, ancil-
lary service support and the idea to provide the storage
device for leveling the output power of the DG units. The
optimal allocation for reliability concerns is another im-
portant factor related with DG technology improvement
as in [9-13], more specifically about the DG contribution
to primary frequency control [14]. The most comprehen-

Y. S. QUDAIH ET AL. 214
sive result was achieved by Thong et al. as they intro-
duce the distributed generation to support and provide
ancillary services for the power system in terms of DG
systems voltage support capability, loss compensation
and stability support capability [15]. According to [16],
authors compare the network performance between the
installation of DG and compensating capacitor for loss
minimization. Also, a plenty of researches discuss the
replacement of capacitor such as in [17-19] that inspire
related studies for DG allocation. However, again, those
methods even for capacitors allocations and related stud-
ies for DG allocation are highly computationally de-
manding. In addition, many other studies discuss auxil-
iary systems such as energy capacitor system (ECS), to
be involved in solving the problems of DG influences.
However, such a study doesn’t consider the power losses
issue if the location of the ECS changes [20].
Intelligent applications are also involved in solving the
matter of DG size and deployment such as using genetic
algorithm (GA), artificial neural network (ANN) and
particle swarm optimization (PSO) as in [21-23], respec-
tively. Unlike other researches which implement intelli-
gent systems to solve the equations of the system with
respect to the problem or to create the suitable control to
the system’s behaviors, this study presents a completely
different policy by developing a new powerful tool to
solve the problem directly without being involved in the
mathematical structure of the system. Especially for the
ANN methods, they have simpler computational tech-
niques and higher pattern recognition abilities than other
optimization method [24,25]. Moreover, this method does
not require knowledge on internal system behavior; re-
quires less computational effort and provides compact
solutions for multi-objective problems [26]. In some
cases, only training process is required and the optimum
point is directly determined without solving any non-
linear mathematical equations or statistical assumptions
as in the conventional optimization methods [27]. For
these reasons, the ANN methods is suitable to estimate
the voltage profile and total power losses under connec-
tion of DG units where their outputs are intermittent and
fluctuated based on environmental conditions.
In this study, the variant of ANN methods called radial
basis function (RBF) neural network is utilized as a
computational tool to assess the existence of DG unit.
There are two structures for this purpose under the same
input signals. The input signal is denoted as the potential
size of DG unit in 33 nodes that can be considered as the
domain operating condition of the proposed structure.
The first structure is for the optimal measurement of
voltage profile in 33 nodes and the second structure is
only for the optimal power losses measurement. Basi-
cally, one single RBF structure can be created for this
study; however the over-fitting condition may occur
during the validation step. In comparison with other
ANN structure, like three layered feed-forward network
(TFFN) and adaptive neuro-fuzzy inference system
(ANFIS) methods, the RBF method is recognizably fast
during the training process and the structure in terms of
number of hidden neurons is directly confirmed soon
after the training process. The accuracy of this technique
is noticeably high during the validation process which is
similar to ANFIS network outcomes [28]. For utilizing
this technique, only training process is required and after
the structure is confirmed; wide different scenarios can
be set including finding the optimal size and location of
DG unit. The only drawback of this method that may be
encountered is the difficulty in dealing with different
objective of studies. But, again only training process is
necessary to solve this change; therefore the method is
flexible and reliable to solve different cases, targets and
scenarios.
The paper is divided into five sections. Section 1
reviews the DG and their influences. It also provides an
overview of other previous researches and the methods
on how to find the optimal size and location of DG unit
in different objectives. Section 2 describes the case study
in terms of system configuration and the way to approach
the load flow study. Our intentions from this part is to
obtain the load flow result as training data set which may
represent the voltage profile and total power losses as the
function of DG sizing in each bus. Then, the RBF struc-
ture which covers the training procedure and validation
process will be explained in Section 3. Section 4 provi-
des the simulation results including discussion part. Fi-
nally, the conclusion is drawn in Section 5.
2. Case Study
The target of the proposed design is the 33-nodes IEEE
distribution system. Therefore, it is necessary to generate
the power flow data of this system using the data shown
in Table 1 [29].
Two outcomes are expected from the load flow study;
i.e., voltage magnitudes and total power losses based on
the certain limit of DG size in each node as the ope-
rating condition of the entire network. The procedure to
calculate the total power losses is explained as follows
and inside the mathematical equations, the voltage mag-
nitude is also explicitly obtained.
In this study, a set of simplified feeder-line flow for-
mulations is employed [30]. Considering the single-line
diagram depicted in Figure 1.
The recursive Equations (1-3) are used to compute the
power flow. For the sake of simplicity, some assump-
tions have been taken into account that may be considered

Y. S. QUDAIH ET AL. 215
Table 1. The 33-bus distribution system data.
Load at receiving end
Line no. From bus To bus Resistance (Ω) Reactance (Ω) Real power (MW) Reactive power (MVAr)
1 1 2 0.0922 0.0477 0.1 0.6
2 2 3 0.493 0.2511 0.09 0.04
3 3 4 0.366 0.1864 0.12 0.08
4 4 5 0.3811 0.1941 0.06 0.03
5 5 6 0.819 0.707 0.06 0.02
6 6 7 0.1872 0.6188 0.2 0.1
7 7 8 1.7114 1.2351 0.2 0.1
8 8 9 1.03 0.74 0.06 0.02
9 9 10 1.04 0.74 0.06 0.02
10 10 11 0.1966 0.065 0.045 0.03
11 11 12 0.3744 0.1238 0.06 0.035
12 12 13 1.468 1.155 0.06 0.035
13 13 14 0.5416 0.7129 0.12 0.08
14 14 15 0.591 0.526 0.06 0.01
15 15 16 0.7463 0.545 0.06 0.02
16 16 17 1.289 1.721 0.06 0.02
17 17 18 0.732 0.574 0.09 0.04
18 2 19 0.164 0.1565 0.09 0.04
19 19 20 1.5042 1.3554 0.09 0.04
20 20 21 0.4095 0.4784 0.09 0.04
21 21 22 0.7089 0.9373 0.09 0.04
22 3 23 0.4512 0.3083 0.09 0.05
23 23 24 0.898 0.7091 0.42 0.2
24 24 25 0.896 0.7011 0.42 0.2
25 6 26 0.203 0.1034 0.06 0.025
26 26 27 0.2842 0.1447 0.06 0.025
27 27 28 1.059 0.9337 0.06 0.02
28 28 29 0.8042 0.7006 0.12 0.07
29 29 30 0.5075 0.2585 0.2 0.6
30 30 31 0.9744 0.963 0.15 0.07
31 31 32 0.3105 0.3619 0.21 0.1
32 32 33 0.341 0.5302 0.06 0.04
Substation voltage-12.66 kV.
upon the application. For instance, the distribution lines
are represented as series impedance; constant load de-
mand and balanced power sink of the values Zi,i+1 = Ri,i+1
+ jXi,i+1 and SL = PLv + jQL, respectively. The real and
reactive power flow at the receiving end of branch i + 1
and the voltage magnitude at the receiving end are res-
pectively expressed by the following equations:
22
11,1
2
ii
iiLiii
i
PQ
PPPR
V


  (1)

Y. S. QUDAIH ET AL. 216
Figure 1. Single-line diagram of the basic feeder in radial
distribution system.
22
11,1
2
ii
iiLiii
i
PQ
QQQX
V


  (2)
22
1,1,1
22
22
,1 ,12
2(.. )
()
iiiiiiii
ii
ii ii
i
VVRPXQ
PQ
RX
V


 

 (3)
Equations (1-3) are known as the distflow equations.
Hence, if P0, Q0 and V0 at node number 1 are estimated,
then the same equations at the other nodes can be calcu-
lated by applying the above branch equations. That is
known as forward update. Similarly a backward update is
applied by the following set of equations:
'2 '2
11,1
2
ii
iLiii
i
PQ
PPP R
V


  (4)
'2 '2
11,1
2
ii
iiLiii
i
PQ
QQQ X
V


  (5)
22 ''
11,1,1
'2 '2
22
-1, -1,2
2(..)
()
iiiiiii
ii
ii ii
i
VVRPXQ
PQ
RX
V

 

 (6)
Where, '
iiLi
PPP and '
iiLi
QQQ .
The power loss of the line section connecting between
buses i and i+1 is calculated as:
22
,1 2
(, 1)ii
Lossi i
i
PQ
Pii R
V


 (7)
Total power loss in the base case and in the case of
diesel generator will be calculated by summing the
whole losses of all sections of the feeder as:

1
,
0
,1
n
Loss TLoss
i
PPii



 (8)
Based on the above mathematical model, Matlab/
Simulink model has been developed [31]. The expected
load power flow measurement are the voltage profile in
each bus and the total power losses as the size of DG unit
is varied in every location inside the network. The opti-
mal size and location of the next DG unit can be found
using the proposed algorithm without any need to repeat
the power flow calculations or the training process, as
will be explained in the next sections. These outcomes
will be used as the training data patterns in the next sec-
tion. The reason of transforming this model into intelli-
gent techniques model is because of the slowness in time
simulation. In the conventional model, it takes some
times to wait until the objectives of power flow result for
one operating condition are confirmed. With intelligent
method, the entire computational burden will be avoided
and the model will be flexible to deal with different sce-
narios.
3. RBF Neural Network Structure
RBF neural network is a typical neural network structure
using local mapping instead of global mapping as in
multi layer perceptron (MLP) [32]. In MLP method, all
inputs cause an output, while in RBF method; only in-
puts near a receptive field produce activation function.
The hidden layer is locally tuned neurons centered over
receptive fields. Receptive fields are located in the input
space areas where input vectors exist. If an input vector
lies near the center of a receptive field, then that hidden
layer will be activated. Because of this approach, the
training process using RBF network is very simple. Once
the set goal error is reached, the training is stopped and
the number of hidden nodes is confirmed.
In this study, two structures of RBF neural network
which is for estimation of voltage profile and total power
loss is developed. Basically, a single structure for this
study can be designed; however much higher error may
occur during the validation process. The basic configura-
tion of the proposed network is shown in Figure 2. In
this figure, there are 33 input signals (N1-N33) for both
estimation purposes that represent the size of the DG unit
for each node. On the other hand, there are 33 output
signals for voltage profile estimation and only a single
output signal for the total losses.
For each task, the development of RBF structure fol-
lows three important stages. They are the establishment
of training data set, training process and validation.
Firstly, the training data set was taken from 33-bus IEEE
test system mentioned in Section 2. This data set is to
cover the entire domain of total losses and voltages as a
function of input power between 0 and 4 MW connected
at every node. For this assumption, there are 133 training
data patterns. The second stage is the training process.
During the training process, the input vector which will
result in lowering the network error is used to create a
new hidden neuron. If the current error after the neuron
insertion is low enough, the training stops. In this study,
the parameter of training process: the mean squared error
goal (GOAL), spread of radial basis functions (SPREAD),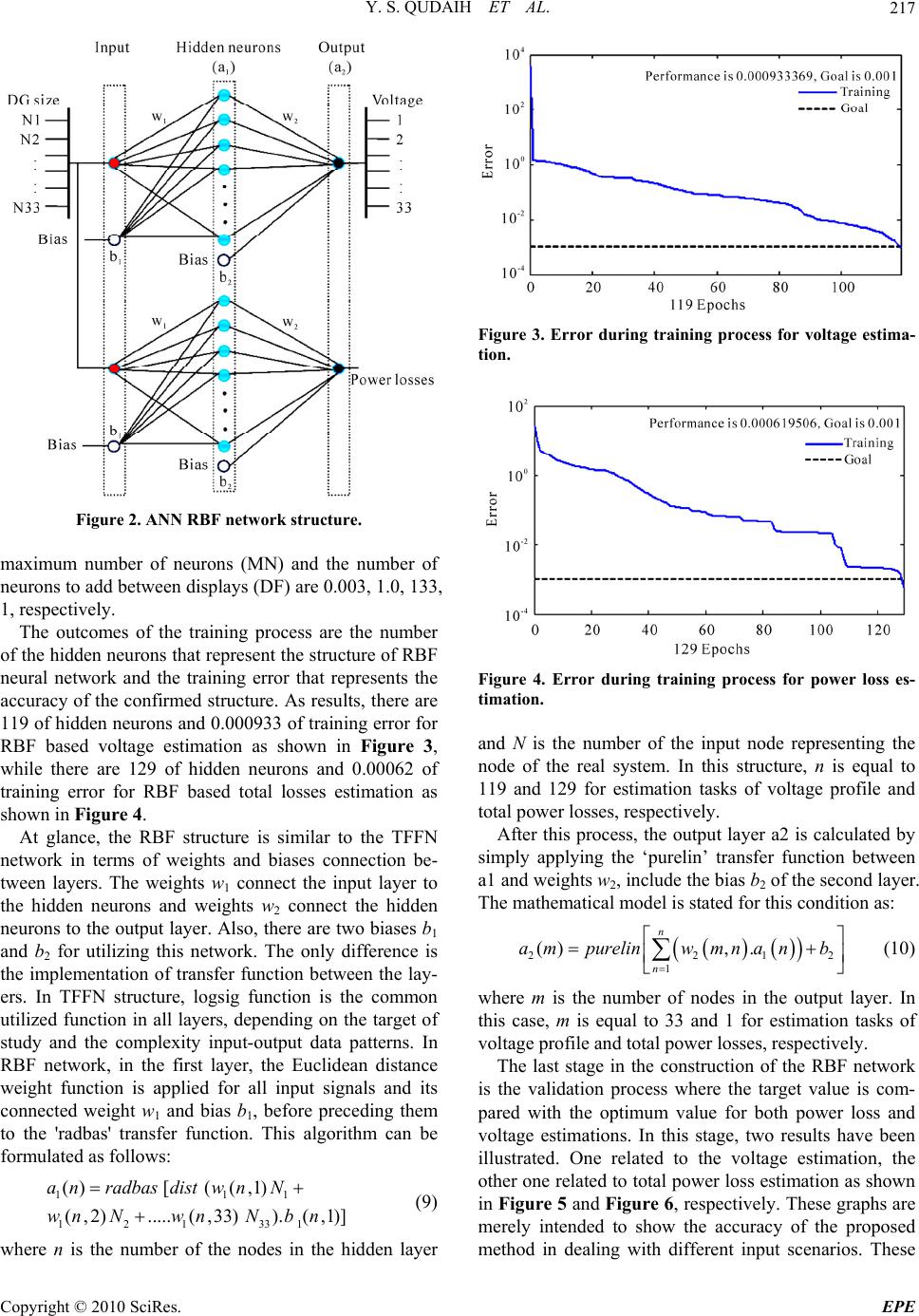

Y. S. QUDAIH ET AL. 217
Figure 2. ANN RBF network structure.
maximum number of neurons (MN) and the number of
neurons to add between displays (DF) are 0.003, 1.0, 133,
1, respectively.
The outcomes of the training process are the number
of the hidden neurons that represent the structure of RBF
neural network and the training error that represents the
accuracy of the confirmed structure. As results, there are
119 of hidden neurons and 0.000933 of training error for
RBF based voltage estimation as shown in Figure 3,
while there are 129 of hidden neurons and 0.00062 of
training error for RBF based total losses estimation as
shown in Figure 4.
At glance, the RBF structure is similar to the TFFN
network in terms of weights and biases connection be-
tween layers. The weights w1 connect the input layer to
the hidden neurons and weights w2 connect the hidden
neurons to the output layer. Also, there are two biases b1
and b2 for utilizing this network. The only difference is
the implementation of transfer function between the lay-
ers. In TFFN structure, logsig function is the common
utilized function in all layers, depending on the target of
study and the complexity input-output data patterns. In
RBF network, in the first layer, the Euclidean distance
weight function is applied for all input signals and its
connected weight w1 and bias b1, before preceding them
to the 'radbas' transfer function. This algorithm can be
formulated as follows:
111
121331
()[( (,1)
( ,2).....( ,33)).(,1)]
anradbasdistw nN
wnNwnNb n

 (9)
where n is the number of the nodes in the hidden layer
Figure 3. Error during training process for voltage estima-
tion.
Figure 4. Error during training process for power loss es-
timation.
and N is the number of the input node representing the
node of the real system. In this structure, n is equal to
119 and 129 for estimation tasks of voltage profile and
total power losses, respectively.
After this process, the output layer a2 is calculated by
simply applying the ‘purelin’ transfer function between
a1 and weights w2, include the bias b2 of the second layer.
The mathematical model is stated for this condition as:
 
2212
1
(), .
n
n
ampurelinwm nanb








 (10)
where m is the number of nodes in the output layer. In
this case, m is equal to 33 and 1 for estimation tasks of
voltage profile and total power losses, respectively.
The last stage in the construction of the RBF network
is the validation process where the target value is com-
pared with the optimum value for both power loss and
voltage estimations. In this stage, two results have been
illustrated. One related to the voltage estimation, the
other one related to total power loss estimation as shown
in Figure 5 and Figure 6, respectively. These graphs are
merely intended to show the accuracy of the proposed
method in dealing with different input scenarios. These

Y. S. QUDAIH ET AL. 218
Figure 5. Validation result for voltage profile after the train-
ing process.
Figure 6. Validation result for total losses after the training
process.
results are highly accurate to be applied in finding the
optimal size and location of DG unit as our main objec-
tives in this study.
4. Results Analysis and Discussion
To reach our objectives in this study, several tests have
been performed in order to find the best solution for op-
timal size and deployment of several DG units. At the
beginning, all inputs from N1 to N33 are zeroed to rep-
resent the base case where no DG is connected. The
simulation runs to find the voltage at every node and the
total losses in the system. After that, the inputs are re-
placed by a ramp function at every node. The data gener-
ated by ramp function is shown in Figure 7 representing
the DG size increased from 0 to 5 MW gradually with a
specified step. The reason of selecting these data ranges
is to match with the maximum load demand of the speci-
fied system and also to implement a variety of DG sizes
with a small step difference. Under this scenarios, the
simulation runs to find the total losses in the system and
the voltage at every node.
The optimum size of DG unit taking the minimum
losses as the reference on each node can be measured by
applying the ramp signal shown in Figure 7 for the con-
structed RBF network presented in Figure 2. Under this
approach, the optimal DG unit size at nodes no. 9, 18 and
32 can be obtained as 1.7, 0.7, 1.1 MW related to a
minimum losses of 139.4, 149.2, 141.1 kW, respectively.
This result is shown in Figure 8, taking the assumption
of distance location; near (node No. 9), middle (node No.
18) and far (node No. 32) from the main source in upper
system. This kind of information is very beneficial to the
utility because the optimal size can be early identified
once there will be a plan to connect DG source at any
location of the network. Again, the proposed method
provides excellent support to test different scenarios
without heavy computational steps. By using this ap-
proach, the optimum size of the DG unit at each location
is illustrated in Figure 9. Similar outcomes in Figure 9
have been achieved as in [3] using analytical method.
However, as mentioned before, that using analytical
technique only provides a single solution for certain ob-
jectives. In fact, our proposed method can handle differ-
ent test scenarios and the result achieved in Figure 9 is
the one solution among the wide range of objectives.
It is shown in Figure 9 that there is a potential to in-
stall higher capacity of DG unit very close to the upper
Figure 7. Input data for the RBF network which represents
the DG sizes.
Figure 8. Total power loss of the system versus DG sizes at
different nodes.

Y. S. QUDAIH ET AL. 219
system, then the size is gradually decreased to the middle
distance of the network. Also, in some locations far away
from the main source, like nodes No. 19, 23, 26 and 27;
the optimal size in medium capacity of DG unit can be
connected under minimum losses. However, these results
do not represent basically the optimal size for the overall
minimum losses of entire network, but only for those
specified locations. Further clarification is necessary to
find the exact position of the DG units in the entire net-
work based on the minimum losses. This concept is
clearly depicted in Figure 10. For instance, the optimal
size of DG unit at node 1 is around 5MW, but the mini-
mum loss of the network under this size is not the lowest
one and so on for other nodes. Based on Figure 10, the
lowest minimum losses is at node No. 6 with the optimal
size of the DG unit equals to 2.66 MW, followed by node
No. 26 with the size of 2.4 MW. Having this information
provides hierarchical locations to install the DG unit,
depending on the availability of power source on the
network. If the main consideration is the minimum power
losses, then nodes 7-18 and nodes 27-33 are the reason-
able options. For instance, the node No. 7 can be the al-
ternative solution with 2.4 MW in optimal size to replace
the location of DG unit in bus 6 due to the abundance of
Figure 9. Optimal size of the DG at every node of the distri-
bution system.
Figure 10. Total minimum power loss of the distribution
system at every node with the 1st DG.
sunlight for PV system or the availability of biomass/fuel
cells source at node No. 7. Especially the group nodes no.
27-33, this is also the other benefits from the proposed
study that there is a high potential to install DG unit far
away from the main source which is a common recent
trend.
The proposed method is properly working to find the
optimal location and size of more than one DG unit in
the distribution system. Following the information in
Figure 9, bus No. 6 is the best location for single DG
unit of 2.6 MW based on the minimum power losses in
Figure 10. For the second unit, the optimal place and
size can be reached by using the same RBF structure
taking the first DG unit into account. The updated chart
for this process is shown in Figure 11. In this figure, the
size of DG at bus No. 6 is zero because the first unit is
already installed there. As results, the DG units of 0.7,
0.6 and 0.6 MW are optimally located in the buses 16, 17
and 18, respectively. The related minimum losses are
shown in Figure 12. The advantage of this method is no
further training process, therefore the computational
process is fast and it has high adaptability and accuracy
to different input scenarios.
As a comparison between the proposed method with
Figure 11. Updated chart for the optimal size of the second
DG at every node of the distribution system.
Figure 12. Total minimum power loss of the distribution
system at every node after installing the second DG unit.

Y. S. QUDAIH ET AL. 220
other methods in terms of performance and consuming
time, Table 2 has been prepared.
In the past, there were debates about system voltage
violation caused by the existence of DG unit. This is
probably true if the optimal size cannot be determined
before connecting the unit to the network. However, if
the proper size can be decided early before the installa-
tion then the presence of DG unit will improve the volt-
age level quality of the entire network. In order to inves-
tigate the voltage profile in the presence of DG systems,
a base case defined as the system without any DG con-
tribution is compared with the cases of optimum DG
connected at the suitable location as declared from the
above discussion. The same nodes 9, 18 and 32 are tested
with the optimal DG capacity presence and the voltage
profile at every bus is measured to conclude that the
voltage profile of the system is not only kept in the range
but noticeably improved. Figure 13 shows that without
DG unit the voltage level at node 18 reaches 0.915 p.u
which may be critical within the permitted range. This
problem can be solved by installing a unit of 1.1MW at
node No. 32. The significant voltage improvement of this
point is observed when the location of unit much closer
to the upper system (DG unit at node No. 9). For other
cases, this method can prepare a look up chart showing
all voltage ranges with respect to the presence of optimal
DG unit to survey for the best voltage profile. Therefore,
the only condition to be provided to reach the voltage
improvement in this study is the installation of optimal
size DG unit in the right location.
Another important result from our proposed method is
that the voltage profile of the entire network can be mo-
nitored as the DG size is changed in specified location.
The 3-D graph in Figure 14 shows the placement of DG
unit at node No. 18. In the figure the x-axis represents
the location which is the 33 nodes of the real system and
N1 to N33 in the RBF neural network, y-axis represents
the size of the DG incremented with a specified step
from 0 to 5 MW ramp function, that representing the
power injected to the system, and z-axis represents the
voltage at every node of the system in per unit. It is no-
ticeable that there is no sign of voltage violation during
the process till the optimum size of the DG is achieved
which implies that DG contribution does not affect the
voltage of the distribution system during loss reduction
process in the steady state condition. Again, this result is
obtained fast without having any computational burdens.
5. Conclusions
This paper reports a simple and well defined approach to
solve the problem of multi DG deployment. RBF Neural
network structure has been developed to achieve the goal
of this paper in a short and easy way. Different sizes of
Table 2. Comparison results.
Power Loss (KW) CPU Time (s)
Base Case 211 --
Proposed Method One DG 139.4 2.9
Proposed Method Multi-DG68 2.9
ABC [30] 139.5 5.3
TFFN 139.4 > 500
Figure 13. Voltage profile of the system in the base case
compared with the optimum DG placed at different loca-
tions.
Figure 14. Voltage profile of the system with DG allocated
at Node 18.
the DG were considered in the form of incrementally
ramp function to the RBF neural network in order to de-
termine the optimal size of the first DG and other DG
units will be found gradually. The optimal size of DG
units is the one at the node of minimum power loss and
non-violated voltage. RBF neural network appears as an
efficient and simple method to find the optimal size and
allocation of the distribution system and to monitor the
voltage profile in the same time. By applying such a

Y. S. QUDAIH ET AL. 221
scenario the optimal size and deployment of DG units in
the medium tension distribution networks can be easily
found. In addition, the contribution of dispersed power
sources technology in reducing power losses and en-
hancing the voltage profile is proved.
6. References
[1] A. Keane and M. O’Malley, “Optimal Allocation of Em-
bedded Generation on Distribution Networks,” IEEE
Transactions on Power Systems, Vol. 20, No. 3, 2005, pp.
1640-1646.
[2] C. Wang and M. H. Nehrir, “Analytical Approaches for
Optimal Placement of Distributed Generation Sources in
Power Systems,” IEEE Transactions on Power Systems,
Vol. 19, No. 4, 2004, pp. 2068-2076.
[3] N. Acharia, P. Mahat and N. Mithulananthan, “An Ana-
lytical Approach for DG Allocation in Primary Distribu-
tion Network,” Electrical Power and Energy Systems,
Vol. 28, No. 10, 2006, pp. 669-678.
[4] K. Nara, Y. Hayashi, B. Deng, K. Ikeda and T. Ashizawa,
“Optimal Allocation of Dispersed Generators for Loss
Minimization,” Electrical Engineering in Japan, Vol. 136,
No. 2, 2001, pp. 1-8.
[5] M. H. Narazi and M. Parniani, “Determining and Opti-
mizing Power Loss Reduction in Distribution Feeders due
to Distributed Generation,” Power Systems Conference
and Exposition, IEEE PES, Atlanta, 2006, pp. 1914-1918.
[6] M. A. Kashem, A. D. T. Le, M. Negnevitsky and G. Led-
wich, “Distributed Generation for Minimization of Power
Losses in Distribution Systems,” IEEE Power Engineer-
ing Society General Meeting, Art. No. 1709179, 2006.
[7] A. D. T. Le, M. A. Kashem, M. Negnevitsky and G.
Ledwich, “Optimal Distributed Generation Parameters
for Reducing Losses with Economic Consideration,”
IEEE Power Engineering Society General Meeting, Art.
No. 4275824, 2007, pp. 1-8.
[8] D. Gautam and N. Mithulananthan, “Optimal DG Place-
ment in Deregulated Electricity Market,” Electric Power
Systems Research, Vol. 77, No. 12, 2007, pp. 1627-1636.
[9] C. L. T. Borges and D. M. Falcão, “Optimal Distributed
Generation Allocation for Reliability, Losses, and Volt-
age Improvement,” Electrical Power and Energy Systems,
Vol. 28, No. 6, 2006, pp. 413-420.
[10] D. Trebolle, T. Gómez, R. Cossent and P. Frías, “Distri-
bution Planning with Reliability Options for Distributed
Generation,” Electric Power Systems Research, Vol. 80,
No. 2, 2010, pp. 222-229.
[11] M. Fotuhi-Firuzabad and A. Rajabi-Ghahnavie, “An Ana-
lytical Method to Consider DG Impacts on Distribution
System Reliability,” Proceedings of the IEEE Power En-
gineering Society Transmission and Distribution Confer-
ence, Art. No. 1547168, 2005, pp. 1-6.
[12] I.-S. Bae, J.-O. Kim, J.-C. Kim and C. Singh, “Optimal
Operating Strategy for Distributed Generation Consider-
ing Hourly Reliability Worth,” IEEE Transactions on
Power Systems, Vol. 19, No. 1, 2004, pp. 287-292.
[13] Y. Yue, Q. Kejun and Z. Chengke, “The Effect of Dis-
tributed Generation on Distribution System Reliability,”
Proceedings of the Universities Power Engineering Con-
ference, Art No. 4469070, 2007, pp. 911-916.
[14] J. Morren, S. W. H. de Haan and J. A. Ferreira, “Contri-
bution of DG Units to Primary Frequency Control,”
European Transaction on Electrical Power, Vol. 16, No.
5, 2006, pp. 507-521.
[15] V. van Thong, J. Driesen and R. Belmans, “Using Dis-
tributed Generation to Support and Provide Ancillary
Services for the Power System,” International Confer-
ence on Clean Electrical Power, ICCEP’07, Art. No.
4272375, 2007, pp. 159-163.
[16] S. Rhim, T. Rahman, I. Musirini, S. Azmi, M. Mohamed,
M. Hussain, M. Faridun, “Comparing the Network Per-
formance Between the Installation of DG and Compen-
sating Capacitor Using EP,” International Journal of
Power, Energy and Artificial Intelligence, Vol. 1, pp 14-
21.
[17] H. N. Ng, M. M. A. Salama and A. Y. Chikhani, “Classi-
fication of Capacitor Allocation Techniques,” IEEE
Transactions on Power Delivery, Vol. 15, No.1, 2008, pp.
387-392.
[18] Y. T. Hsiao and C. Y. Chien, “Optimisation of Capacitor
Allocation Using an Interactive Trade-off Method,” IEE
Proceedings, Generation, Transmission and Distribution,
Vol. 148, No. 4, 2001, pp. 371-374.
[19] M. Delfanti, G. P. Granelli, P. Marannino and M. Mon-
tagna, “Optimal Capacitor Placement Using Determinis-
tic and Genetic Algorithms,” IEEE Transactions on
Power Systems, Vol. 15, No. 3, 2000, pp. 1041-1046.
[20] Y. Qudaih and T. Hiyama, “Reconfiguration of Power
Distribution System Using Multi Agent and Hierarchical
Based Load Following Operation with Energy Capacitor
System,” Proceedings of the 8th International Power En-
gineering Conference, Singapore, 2007, pp. 263-267.
[21] V. Calderaro, A. Piccolo and P. Siano, “Maximizing DG
Penetration in Distribution Networks by Means of GA
Based Reconfiguration,” International Conference on
Future Power Systems, Art. No. 1600510, 2005.
[22] J. N. Fidalgo, J. A. F. M. Torres and M. Matos, “Fair
Allocation of Distribution Losses Based on Neural Net-
works,” International Conference on Intelligent Systems
Applications to Power Systems, Art. No. 4441685, 2007,
pp. 1-6.
[23] W. Prommee and W. Ongsakul, “Optimal Multi-Distrib-
uted Generation Placement by Adaptive Weight Particle
Swarm Optimization,” International Conference on Con-
trol, Automation and Systems, Korea, 2008, pp. 1663-
1668.
[24] A. Mellit and S. A. Kalogirou, “Artificial Intelligence
Techniques for Photovoltaic Applications: A review,”
Progress in Energy and Combustion Science, Vol. 34, No.
5, 2008, pp. 574-632.
[25] A. Mellit, S. A. Kalogirou, L. Hontoria and S. Shaari,

Y. S. QUDAIH ET AL. 222
“Artificial Intelligence Techniques for Sizing Photo-
voltaic Systems: A review,” Renewable and Sustainable
Energy Reviews, Vol. 13, No. 2, 2009, pp. 406-419.
[26] F. Giraud and Z. M. Salameh, “Analysis of the Effects of
a Passing Cloud on a Grid-Interactive Photovoltaic Sys-
tem with Battery Storage Using Neural Networks,” IEEE
Transactions on Energy Conversion, Vol. 14, No. 4, 1999,
pp. 1572-1577.
[27] A. Mellit, M. Benghanem and S. A. Kalogirou, “An
Adaptive Wavelet-Network Model for Forecasting Daily
Total Solar-radiation,” Applied Energy, Vol. 83, No. 7,
2006, pp. 705-722.
[28] Syafaruddin, E. Karatepe, T. Hiyama, “Feasibility of
Artificial Neural Network for Maximum Power Point Es-
timation of Non Crystalline-Si Photovoltaic Modules,”
The 15th ISAP Conference, Curitiba, 2009.
[29] M. E. Baran and F.Wu, “Network Reconfiguration in
Distribution System for Loss Reduction and Load Bal-
ancing,” IEEE Transactions on Power Delivery, Vol. 4,
No. 2, 1989, pp. 1401-1407.
[30] R. Srinivasa, S. V. L. Narasimham and M. Ramalingaraju,
“Optimization of Distribution Network Configuration for
Loss Reduction Using Artificial Bee Colony Algorithm,”
Proceedings of World Academy of Science, Engineering
and Technology, Vol. 35, 2008, pp. 709-715.
[31] Y. Qudaih and T. Hiyama, “Wealth in DG Diversity for
Power Distribution System Operation Improvement,”
Transmission & Distribution Conference & Exposition:
Asia and Pacific, Dalian, 2009, pp. 1-4.
[32] A. Mellit, M. Menghanem and M. Bendekhis, “Artificial
Neural Network Model for Prediction Solar Radiation
Data: Application for Sizing Standalone Photovoltaic
Power System,” Proceedings of IEEE Power Engineering
Society General Meeting, Vol. 1, 2005, pp. 40-44.