Paper Menu >>
Journal Menu >>
 Int. J. Communications, Network and System Sciences, 2010, 3, 893-898 doi:10.4236/ijcns.2010.311121 Published Online November 2010 (http://www.SciRP.org/journal/ijcns) Copyright © 2010 SciRes. IJCNS Consensus of a kind of Dynamical Agents in Network with Time Delays Hongwang Yu, Baoshan Zhang School of Mathematics and Statistic, Nanjing Audit University, Nanjing, China E-mail: yuhongwang@nau.edu.cn Received August 4, 2010; revised September 18, 2010; accepted October 23, 2010 Abstract This paper investigates the collective behavior of a class of dynamic agents with time delay in transmission networks. It is assumed that the agents are Lyapunov stable distributed on a plane and their location coordi- nates are measured by some remote sensors with certain error and transmitted to their neighbors. The control protocol is designed on the transmitted information by a linear decentralized law. The coordination of dy- namical agents is shown under the condition that the error is small enough. Numerical simulations demon- strate that our theoretical results are valid. Keywords: Multi-Agent System, Time Delay, Consensus Protocol 1. Introduction Distributed coordination of network of dynamic agents has attracted a great attention in recent years. Modeling and exploring these coordinated dynamic agents have become an important issue in physics, biophysics, sys- tems biology, applied mathematics, mechanics, computer science and control theory [1-10]. How and when coor- dinated dynamic agents achieve aggregation is one of the interesting topics in the research area. Such problem may also be described as a consensus control problem. To describe the collective behavior of agents in a large scale network, the agent in the network usually is mod- eled by a very simple mathematical model, which is an approximation of real objects. Saber and Murray [3,4] proposed a systematical framework of consensus prob- lems in networks of dynamic agents. In their work the dynamics of the agent is modelled by a simple scalar continuous-time integrator x u , the convergence analysis is provided in different types of the network topologies. Following the work of [2,3], G. Xie and L. Wang [8] study the case where the dynamics of each agent is second order. In their work, they show that by means of a simple linear control protocol based on the structure of the graph, the dynamical agents will eventu- ally achieve aggregation, i.e., all agents will gradually move into a fixed position of the line, meanwhile their velocities converge to zero. In networks of the dynamic agents, time delays and sensor error may arise naturally, e.g., because of the moving of the agents, the congestion of the communica- tion channels and the finite transmission speed due to the physical characteristics of the medium transmitting the information. The different protocols with time delays have been investigated [2,4]. And the sensor error or communicated errors are also to be considered in the consensus protocol [9]. It is shown that the collective behavior of dynamical agent will depend on the commu- nicated error and the algebraic characterization of the communicated network topology. In this paper, we study the consensus of multiagent systems where the dynamics of each agent is second or- der. The agents may represent the vehicles or mobile robots spread over a wild area and they communicate by means of some remote sensors with certain error and time delay. When the agents are moving in a plane, the consensus conditions will depend on the time delay, communicated error and the algebraic characterization of network topology, as well as the dynamical behavior of agents. This paper is organized as follows. In Section 2, we recall some properties on graph theory and give the problem formulation. In Section 3 the main results of this paper are given and some simulation results are pre- sented in Section 4. Final section is a conclusion.  894 H. W. YU ET AL. 2. Preliminaries By , we denote an undirected graph with an weighted adjacency matrix (, , )GVEA [] ij A a EVV , where is the set of nodes, is the set of edges. The node indexes belong to a finite index set 1 {, ,} M Vp p 1, , M M . An edge of G is denoted by . The adjacency elements are defined in following way: (, ji )p ij eE ij ep ij a . Moreover, we assume for all 0 ij a 0 ii aiM . The set of neighbors of node is denoted by i p |( ij NpV , i p) j pE Ddiagd . A diagonal matrix is a degree matrix of G with . Then the Laplacian of the ,,d 1M 1 M iij j da weighted graph G is defined as . A graph is called connected if there exists a path between any two distinct vertices of the graph. LDA An important fact of L is that all the row sums are zero, therefore, is an eigenvector of L associ- ated with zero eigenvalue. Moreover, the graph G is connected if and only if its Laplacian L is satisfied rank(L) = M − 1 and all eigenvalues of L are of positive real numbers except that only one eigenvalue is zero [2]. 11,,1 T M Consider a network of dynamical agents defined by a graph . The node set V consists of dy- namical agents (, , )GVEA , i Pi M. Let 2 12 (, ) T iii x xx R P be the coordinate of dynamical agent i, then the dynamics of are identical and described as follows. i p ii iii i i ii x v mvKv u x yF v (1) where i x is indicates the location vector of agent i in the plane, represents its velocity vector p 12 (, ) T iii vvv of the ith agent, is its mass and is i m11 12 21 22 kk Kkk a dynamical feedback matrix of the agent. F is an obser- vation matrix of the agent by some remote sensor. In what follows we simply assume that and ii 1 i mpx . Let which means that the location informa- tion of the ith agent is only measured by some remote sensor and is transmitted to its neighbors through the network. The matrix C is assumed to be the form [0]FC 1 1 i i C . The parameter i indicates that the network communicated error or the coordinates used for sensor could be different from that of the agents. For the dynamic agent (1) in network we have follow- ing assumption. Assumption 1. The dynamics (1) is Lyapunov stable when it disconnected with its neighbors, meaning that the dynamical agent as an autonomous will gradually stop by moving a finite distance for any non-zero initial velocity. We shall give the conditions, under which the network of dynamical agents (1) achieve asymptotical consensus meaning that there exists a fixed position (equilibrium) such that for 2 RxiM 21 lim( ) lim( )0 i t i t x tx vt (2) Due to time-delay in communicated network, the con- trol protocol of the dynamical agent i is a neighbor- based linear control law in the form that p (( ())( ())) ji iijjijiij pN uayttytt (3) where i is the set of neighbors of agent i and ij are adjacency elements of A. The N p a() 0 ij t , denoting the communication transmission time-delay from agent j p to agent i. In this paper, we discuss the consensus of dynamical agent under the condition of the communi- cated error and the time delay. We focus on the simplest possible case where the time-delays in all channels are equal to p and the communicated errors are equal to . Remark 1. If we choose 0 and 11 22 kkk , 1221 0kk , then the two-dimension agent systems (1) with the control protocol (3) can be decoupled into two identical linear systems and it was discussed by some literatures with or without time delays( such as [8,9]). 3. Consensus of Dynamic Agents We denote the initial locations and the initial velocities of the agents by 1 (0) ( (0)(0)) TT M xx xT 1 (0) ( (0)(0)) TT M vv v , T respectively. Under control protocol (3) with () ij t , the dynamical equation of agent is written by i p ()()( ()()) ji iiijj i pN tAtB att where , () ( (),()) TT iii txtvt T iM 22 22 22 0 0 I A K , . (4) 22 22 22 22 00 0 BI T Furthermore, let 1, then the dynamic network is of the following form () ((),,()) TT M tt t 12 ()()( )ttt (5) where 12 , M I ALB (6) Copyright © 2010 SciRes. IJCNS  H. W. YU ET AL. 895 And L is the Laplacian associated with the connected graph G. Because (5) is a standard linear time-delay dy- namical systems, its stability analysis is equivalent to analyzing the eigenvalues and eigenvectors of matrix . 12 Lemma 1. The matrix 12 has two eigen- vectors associated with zero eigenvalue. Let e e , be the left and right eigenvectors (denoted by matrices) of matrix associated with zero eigenvalue, respectively. Then 22 11 T TM K I M , 1 22 110 M K M (7) and 22 I , where 11,,1 T M MR. Proof It is well known that (refer to [2,11]) the graph is connected if and only if its Laplacian satisfies that rank(L) = M − 1. Moreover, is an eigenvector of L associated with zero eigenvalue. Then, there is only one zero eigenvalue of L, all the other ones are positive and real. By the definition of (6) and , one has (, ,)GVEA 1 e 11,,1 T M 2 22 12 22 22 22 22 22 22 22 22 22 42 11 0 110 00 110 0 M M M T TM T TM KI e M I IKI K M eLeLKII M Thus, 22 11 T TM K I M represents the two left eigenvectors of . Similarly, it is easy to check 42 0M , which im- plies that 1 22 110 M K M represents two left- eigenvectors of . And it is holds that 22 I . Theorem 1 If the dynamical feedback matrix K in dynamical agent (1) satisfies Assumption 1, i in the C of (1) and the time delays () ij t in (3) satis- fies min max (8) with min 22 2( ) abc d eab , max 22 2( ) abc d eab (9) where , ,, and 21 12 ak k 22 ()4(e a 11 22 bkk 22 )bb c11 2212 21 ckkkk d abc M denotes the biggest eigenvalue of matrix L, then all of the eigen- values of 12 e 0 defined in (6) are of negative real parts except for only two zero eigenvalues. Proof As the graph G is connected, one denotes the eigenvalues of L by 12M . There exists an orthogonal matrix W such that 12 {, ,,} M iag T WLW d 44 44 44 44 () () 00 M T T WI W WII AeB . One can verify the following formulae. 44 44 144 44 2 44 44 () ( )( 00 00 M I AeLBWI AeB ) A eB Then the dynamical behavior of the network (1) is char- acterized by the eigenvalues of , iiMAeB . First we discuss the block with 10 . By Assump- tion 1, one has 1122 0,kk12211122 kk kk (10) and 1 ()Ae B rank 2 12 0, (ss , its four eigenvalues satisfy 3 4 ) 0,() 0Res Res For 0 i , one has 22 2 0 ii I AB C eek . As ()rank C2 , then . Therefore, 12 () i AeB rank 4 e has only two zero eigenvalues. Consider the characteristic polynomial of i A Be for iM . 11 12 21 22 43 2 1234 ()( ()) 010 00 i AB i ii ii sdetsIA B s s1 s kk ksk e ee e s e asasas a where 11122211 221221 321121122 22 2 4 , 2 ()()], ( , [ 1) i i i e e akkakkkk akk e kk a (11) Construct the Routh array of () i AB s 4 24 3 13 2 12 1 1 0 1 1 0 0 0 aa s aa sbb s c s d s Copyright © 2010 SciRes. IJCNS  896 H. W. YU ET AL. with 22 2 12 3 1214 1 , i aa a bbdae a (1), 22 131212331 4 1 111 . ba abaaa aaa cbab By the criterion, for stability it is necessary that 111 1 . Therefore, the dynamical network is stable if and only if the following inequalities hold Routh Hurwith 0, 0,ab0, 0 cd 1 4 12 3 22 12331 4 0 0 0 0 a a aa a aaaaa a (12) By (10) and (11), it is obvious that the first and second inequalities in (12) hold, and one may easily verify that the third inequality in (12) holds only if the fourth ine- qualities holds. Then 22 12331 4 112211 2212212112 222 22 1122112221 12 {()() [() ()]} [()( ii aaaaa a kk kkkkkk kk eekkkk )] 2 So the fourth inequality in (12) can be rewritten as the following form. 222 (0) ii i bc abceab (13) where 2112 , ,. From it, one may obtain ak k 11 22 bkk 11 2212 21 ckkkk 22 22 2( )2( ii i ii abc dabc d eab eab ) 2 where . Under the case, the matrix i 222 ()4 () ii dabceabb c A Be is H urwith. Then it is obvious that the matriies i A Be are H urwith for all under the condition of (8) and (9). There- fore, all of the eigenvalues of the matrix 12 defined in (6) are of negative real parts except for only two zero eigenvalues. 2,i,M e Theorem 2 Under conditions of Theorem 1, the con- trol protocol (3) globally and asymptotically achieves the collective behavior of the dynamic agents. Proof Under conditions of Theorem 1, all of the ei- genvalues of the matrix 12 defined in (6) are of negative real parts except for only two zero eigen- values. By e 4 14 , ,,)44 12 :(, M M R MM one denotes right-eigenvectors of associated with eigen- values 12 2 ,,, M respectively. It holds that , 22 1, 1 0,,, M diagJ J J denotes the Jordan form of two order associated with the eigenvalues 1 and 2 . i J denotes the Jordan form of four order associated with the eigenvalues 43 4241 ,, iii and 4i for all . 2, ,iM 414 , ) Let 14 :(, , TT 4 12 , M M R MM TT T , where ;4 ii M are 4 M row left-eigenvectors of correspondingly. Then it is holds that . 41 (Re R As 34 )( 4 ) )( MM Re e0(Re) 2(42) 42)(42) M M )2( 0 00 MM , one has 22 (42 I limJt te 2(4 2) (42)(42 0 00 M MM and 22 42)2 )M ( I lim( ) texp t Let 12 () and 2 1 , one has li tm()exp t . Due to the fact that 1 44 ·· M M I , and satisfy the property 22 I . 1 22 2 22 ( 0 exp k 2 (0 ) ·( ·(0) kI 1 22 lim()lim)(0) 10) 1 00 tt MM MM t t M Ik M 11 11 Therefore, 1 (0) ( ij x kv , 2,,} M 1 1 lim ({[0)]} M j tj xt M ) 0, and it is obvious that lim( ){1 i tvt i This implies the protocol (3) globally asymptotically achieves the collective behavior of the dynamic agents. Corollary 1 The dynamical feedback matrix K is chosen to be 1221 1 kkk and 11222 , then the control protocol (3) globally and asymptotically achieves the collective behavior of the dynamic agents if the time kkk satisfy 22 21 2 delays ln kk . Proof It is easy to verify according to the proof of Theorem 1 and Theorem 2. Under Assumption 1, one has 122111 22 kk kk . Thus, one finds that and it further implies that min 0c 0 and max 0 in (9) for bounded time delay. Thus we have the following result. Corollary 2 The dynamical agents achieve collective behavior if the network communicated error is suf- ficient small for the bounded time delays. 4. Simulations Numerical simulations will be given to illustrate the theoretical results obtained in the previous section. Con- Copyright © 2010 SciRes. IJCNS 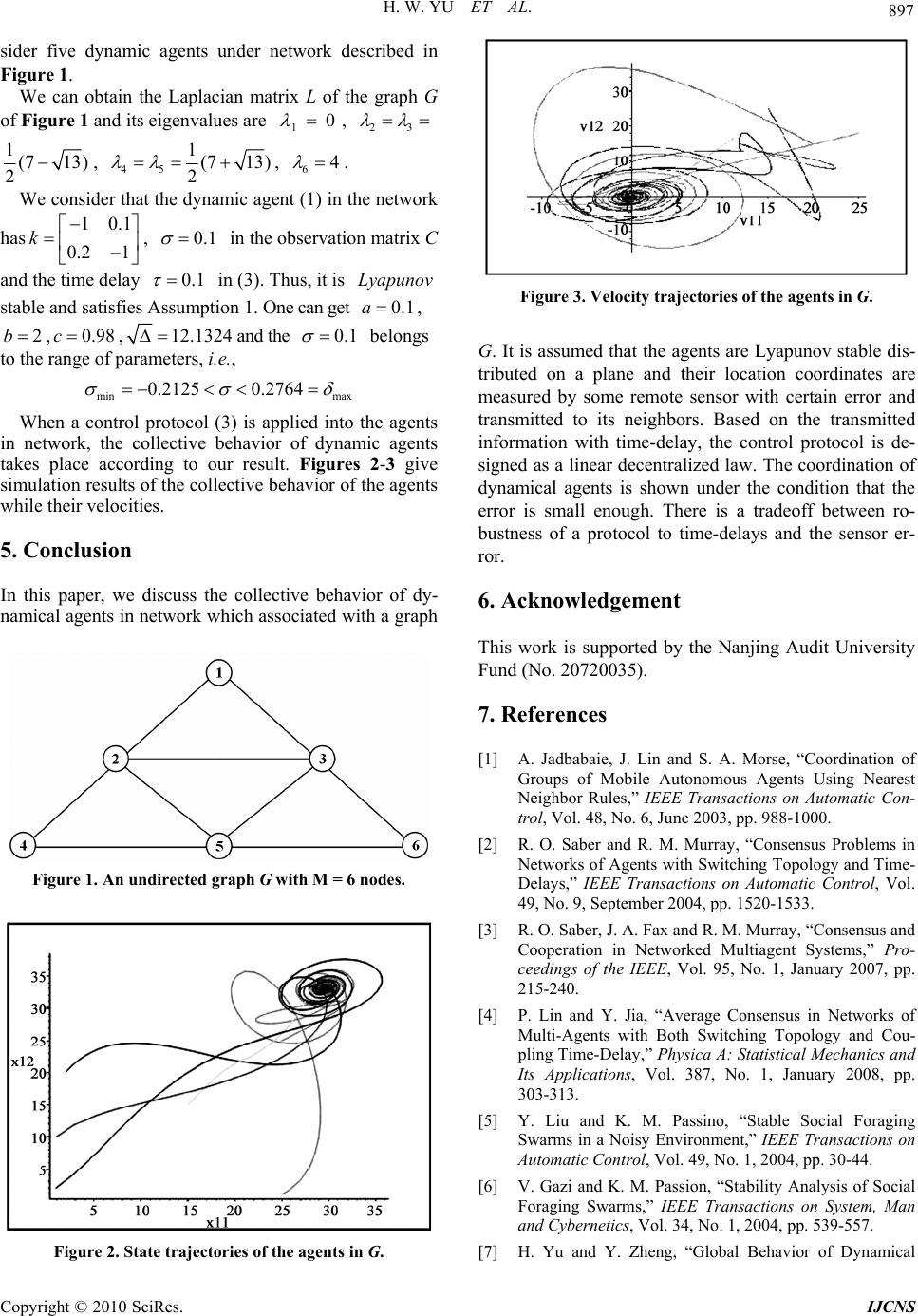 H. W. YU ET AL. 897 sider five dynamic agents under network described in Figure 1. We can obtain the Laplacian matrix L of the graph G of Figure 1 and its eigenvalues are , 10 23 1(713) 2, 45 1(7 13) 2 , 64 . We consider that the dynamic agent (1) in the network has , 10.1 0.2 1 k 0.1 in the observation matrix C and the time delay 0.1 in (3). Thus, it is stable and satisfies Assumption 1. One can get Lyapunov 0.1a , , ,20.98cb12.132 4and the 0.1 belongs to the range of parameters, i.e., min max 0.2125 0.2764 When a control protocol (3) is applied into the agents in network, the collective behavior of dynamic agents takes place according to our result. Figures 2-3 give simulation results of the collective behavior of the agents while their velocities. 5. Conclusion In this paper, we discuss the collective behavior of dy- namical agents in network which associated with a graph Figure 1. An undirected graph G with M = 6 nodes. Figure 2. State trajectories of the agents in G. Figure 3. Velocity trajectories of the agents in G. G. It is assumed that the agents are Lyapunov stable dis- tributed on a plane and their location coordinates are measured by some remote sensor with certain error and transmitted to its neighbors. Based on the transmitted information with time-delay, the control protocol is de- signed as a linear decentralized law. The coordination of dynamical agents is shown under the condition that the error is small enough. There is a tradeoff between ro- bustness of a protocol to time-delays and the sensor er- ror. 6. Acknowledgement This work is supported by the Nanjing Audit University Fund (No. 20720035). 7. References [1] A. Jadbabaie, J. Lin and S. A. Morse, “Coordination of Groups of Mobile Autonomous Agents Using Nearest Neighbor Rules,” IEEE Transactions on Automatic Con- trol, Vol. 48, No. 6, June 2003, pp. 988-1000. [2] R. O. Saber and R. M. Murray, “Consensus Problems in Networks of Agents with Switching Topology and Time- Delays,” IEEE Transactions on Automatic Control, Vol. 49, No. 9, September 2004, pp. 1520-1533. [3] R. O. Saber, J. A. Fax and R. M. Murray, “Consensus and Cooperation in Networked Multiagent Systems,” Pro- ceedings of the IEEE, Vol. 95, No. 1, January 2007, pp. 215-240. [4] P. Lin and Y. Jia, “Average Consensus in Networks of Multi-Agents with Both Switching Topology and Cou- pling Time-Delay,” Physica A: Statistical Mechanics and Its Applications, Vol. 387, No. 1, January 2008, pp. 303-313. [5] Y. Liu and K. M. Passino, “Stable Social Foraging Swarms in a Noisy Environment,” IEEE Transactions on Automatic Control, Vol. 49, No. 1, 2004, pp. 30-44. [6] V. Gazi and K. M. Passion, “Stability Analysis of Social Foraging Swarms,” IEEE Transactions on System, Man and Cybernetics, Vol. 34, No. 1, 2004, pp. 539-557. [7] H. Yu and Y. Zheng, “Global Behavior of Dynamical Copyright © 2010 SciRes. IJCNS  H. W. YU ET AL. Copyright © 2010 SciRes. IJCNS 898 Agents in Directed Network,” Proceedings of the 26th Chinese Control Conference, 2007, pp. 557-561. [8] G. Xie and L. Wang, “Consensus Control for a Class of Networks of Dynamic Agents,” International Journal of Robust and Nonlinear Control, Vol. 16, 2006, pp. 1-16. [9] L. Yang, H. Yu and Y. Zheng, “Aggregation of Dynamical Agents in Network,” 7th World Congress on Intelligent Control and Automation, June 2008, pp. 6348-6352. [10] N. Biggs and Algebraic, “Graph Theory,” Cambridge University Press, Cambridge, 1994. [11] R. A. Horn and C. R. Johnson, “Matrix Analysis,” Cam- bridge University Press, Cambridge, 1987. |

