Int. J. Communications, Network and System Sciences, 2010, 3, 888-892
doi:10.4236/ijcns.2010.311120 Published O nline Novem ber 2010 (http:// www.SciRP.org/journal/ijcns)
Reduction PAPR of OFDM Signals by Combining SLM
with DCT Transform
Zhongpeng Wang
School of Information and Electronic Engineering, Zhejiang University of Science and Technology,
Hangzhou, China
Received July 20, 2010; revised August 31, 2010; accepted October 6, 2010
Abstract
One of main disadvantage of Orthogonal frequency division multiplexing (OFDM) is high peak-to-average power
ratio (PAPR). In this paper, two effective PAPR reduction schemes are proposed. These techniques combine
the DCT and SLM techniques. The scheme 1 is composed of the DCT followed by the SLM technique, and
the DCT is used followed by conventional SLM in proposed scheme 2. Simulation results show that the pro-
posed schemes can obtain significant PAPR reduction performance with that of ordinary SLM techniques.
Keywords: SLM, DCT Transform, PAPR, OFDM
1. Introduction
Orthogonal frequency division multiplexing (OFDM) has
been recently seen rising popularity in wireless applica-
tions. For wireless communications, an OFDM-based
system can provide greater immunity to multi-path fad-
ing and reduce the complexity of equalizers. Now
OFDM have been included in digital audio/video broad-
casting (DAB/DVB) standard in Europe, and IEEE
802.11, IEEE 802.16 wireless broadband access systems,
etc.
However, OFDM also has its shortcoming. The major
drawback of OFDM signal is its large peak-to-average
power ratio (PAPR), which causes poor power efficiency
or serious performance degradation to transmit power
amplifier. To reduce the PAPR, many techniques have
been proposed. Such as clipping, partial transmit sequence
(PTS) [1], selected mapping (SLM) [2], interleaving,
nonlinear companding transforms, hadamard transforms
[3] and other techniques etc [4,5]. These schemes can
mainly be categorized into signal scrambling techniques,
such as PTS, and signal distortion techniques such as
clipping. Among those PAPR reduction methods, the
simplest scheme is to use the clipping process. However,
using clipping processing causes both in-band distortion
and out-of-band distor tion. The bit error rate of system is
degraded by using clipping. The SLM is relatively at-
tractive since it can obtain better PAPR by modifying the
OFDM signal without distortion. The main disadvantage
of SLM is that its complexity is high. Now many exten-
sion schemes for reducing complexity of LSM have been
presented [6,7]. In this paper, an efficient reducing PAPR
technique based on joint SLM and DCT matrix transform
is proposed.
The organization of this paper is as follow. Section 2
presents OFDM signal model and formulates the prob-
lem of PAPR. Section 3, the reduction PAPR schemes
based on combined DCT transform matrix and SLM
technique are proposed. Numerical results are presented
in Section 4. Sect i on 5 draws conclusions.
2. OFDM Signal and Problem Formulation
2.1. OFDM Signal Model and PAPR Problem
In this section, we review the basic of OFDM transmitter
and the PAPAR definition. Consider an OFDM consist-
ing of N subcarriers. Let a block of N symbol


,0,1,,1
k
Xk N

X is formed with each symbol
modulating one of a set of subcarriers.

,
k
f
k


0,1,,1N


fkfk
. The N subcarriers are chosen to be or-
thogonal, that is,


, where and )/(1 NTf 
T
is
the original symbol period. Therefore, the complex
baseband OFDM signal can be written as
NTteX
N
tx tfj
N
kkk 


0 ,
1
)( 2
1
0

(1)
In general, the PAPR of OFDM signals is de-
)(tx

Z. P. WANG
889
fined as the ratio period between the maximum instanta-
neous power and its average power during an OFDM
symbol
2
0
2
0
max( )
PAPR 1/()( )
tNTNT
xt
NTx tdt





 (2)
Reducing themax( )
x
t is the principle goal of PAPR
reduction techniques. In practice, most systems deal with
a discrete-time signal, therefore, we have to sample the
continuous-time signal ()
x
t.
To better approximate the PAPR of continuous-time
OFDM signals, the OFDM signals samples are obtained
by times oversamping. By sampling defined
in Equation (1), at frequenc
L)(tx
y T
s, wher L is
the oversampling factor, the discrete-time OFDM symbol
can be written as
Lf e
10 ,
1
)( 2
1
0
 


NLneX
N
nx kn
NL
j
N
kk

(3)
Equation (3) can be implemented by using a length
(NL) IFFT operation. The new input vector X is ex-
tended from original X by using the so-called
zero-padding scheme, i.e., by inserting ze-
ros in the middle of X. The PAPR computed form the
L-times oversampled time domain OFDM signal sam-
ples can be defined as
NL ）（ 1

2
01
2
max( )
PAPR()10lg()
tNL xn
xn Exn
 





N
(4)
However, the PAPR does not increase significantly
after . In order to avoid aliasing the out-of-band
distortion into the data bearing tones and in order to ac-
curately describe the PAPR an oversampling factor
is required.
4L
4LWe can evaluate the performance of PAPR using the
cumulative distribution of PAPR of OFDM signal. The
cumulative distribution function (CDF) is one of the
most regularly used parameters, which is used to meas-
ure the efficiency of and PAPR technique. The CDF of
the amplitude of a signal sample is given by
)exp(1)( zzF (5)
However, the complementary CDF (CCDF) is used
instead of CDF, which helps us to measure the probabil-
ity that the PAPR of a certain data block exceeds the
given threshold. The CCDF of the PAPR of the data
block is desired is our case to compare outputs of various
reduction techniques. This is given by
()1()
1(())1(1exp( ))
N
PPAPRzPPAPRz
F
z
 
 
2.2. Selected Mapping (SLM)
The SLM technique was first described by Bauml et al.
[3]. In the SLM, the input data sequences are multiplied
by each of the phase sequences to generate alternative
input symbol sequences. Each of these alternative input
data sequences is made the IFFT operation, and then the
one with the lowest PAPR is selected for transmission.
Figure 1 shows the block of the SLM technique. X is the
OFDM data block, u is the phase vectors and u is
the modified data vectors in the frequency domain. So
the time domain signal
B X
NTteBX
N
txftkj
ku
Nk
kku  


0 ,
1
)( 2
,
1
0

(7)
where 1,2,,uU

 and is length of X, also the
number of s ub -carriers. N
Among the modified data blocks, the one with the
lowest PAPR is selected for transmission. The amount of
PAPR reduction for SLM depends on the number of phase
sequences U and the design of the phase sequences.
2.3. DCT Transform
The Discrete Cosine Transform (DCT) is a Fourier-like
transform, which was first proposed by Ahmed et al.
(1974) [8]. The idea to use the DCT transform is to re-
duce the autocorrelation of the input sequence to reduce
the peak to average power problem and it requires no
side information to be transmitted to the receiver. In the
section, we briefly review DCT transform.
The formal definition of the DCT of one-dimensional
of length N is given by the fo llowin g fo rmula:
1
0
(2 1)
() ()()cos2
for 01
N
cn
nk
Xkk xnN
kN











(8)
Similarly, the inverse transformation is defined as
1
0
(2 1)
()()() ()cos2
for 01
N
c
u
nk
xnkkX kN
nN











(9)
For both equations ( ) and ( ) ()u

is defined as
10
() 20
for k
N
u
for k
N








(10)
The equation ( ) is expressed in matrix below
cN
X=Cx (11)
z
(6) where and are both vector with , and
c
Xx1NC
N

Z. P. WANG
890
is a DCT transform matrix with . The row (or
column) of the DCT matrix NN C
N
are orthogonal matrix
vectors. Then we can use this property of the DCT ma-
trix and reduce the pe ak power of OFDM signals.
3. Proposed Schemes
The main idea of the proposed scheme is to use a com-
bination of two appropriate methods. One is the DCT
matrix transform technique and the other is the SLM
technique. The technique is similar to the scheme pro-
posed in literature [6]. The transmitter block is showed in
Figure 1. We call this scheme is scheme 1. In the trans-
mit end, the data stream is firstly transformed by DCT
matrix, then the transformed data is processed by the
SLM unit. If data block passed by DCT matrix before
IFFT, the autocorrelation coefficients of IFFT input is
reduced, then the PAPR of OFDM signal could be re-
duced.
In this paper, we use DCT matrix after SLM to further
reduce the PAPR of signal. We call this scheme as
scheme 2. In his fashion, the autocorrelation of the signal,
which has been processed by SLM, is reduced by DCT
matrix transform. The PAPR of fine output signal is fur-
ther reduced. The block of transmitter is showed in Fig-
ure 2.
4. Simulation Results
In this section, computer simulations are used to evaluate
the peak-to-average ratio reduction capability with pro-
posed scheme. The channel is modeled an additive while
Gaussian noise (AWGN). In simulation, an OFDM sys-
tem is considered with subcarrier and QPSK
modulation. In SLM unit, U different random phase se-
quences are used.
64N
The results of original SLM are given in Figure 3. We
can see that the reduction effect is improved with the
increasing of s ub -block numb er U.
The results of proposed schemes 1 are given in Figure
4 and Figure 5 is the results of proposed scheme 2. From
these figures, we see that our proposed scheme 1 and
scheme 2 for QPSK have better performance than origi-
nal SLM (Figure 3).When U = 2 and CCDF = 10-3, the
proposed scheme 1 may reduces PAPR about 1.8 dB and
the proposed scheme 2 may reduces about 1.2 dB.
Data
Source
IFFT
DCT
Partition
into
blocks
IFFT
IFFT
Sele tio n
optimal
combination
of phase
factors with
lowver PAPR
Parallel to
seri al
X(1)
X(2)
X(u)
B(2)
B(u)
B(1)
Figure 1. Diagram of proposed SLM scheme 1.
Data
Source
IFFT
DCT
transfor m
Partit ion
into bloc ks
and
serial to
parallel
conversion
IFFT
IFFT
Seletion
optimal
combination
of phase
factors with
lowver PAPR
Parallel to
serial
X(1)
X(2)
X(u)
B(2)
B(u)
B(1)
Figure 2. Diagram of proposed SLM scheme 2.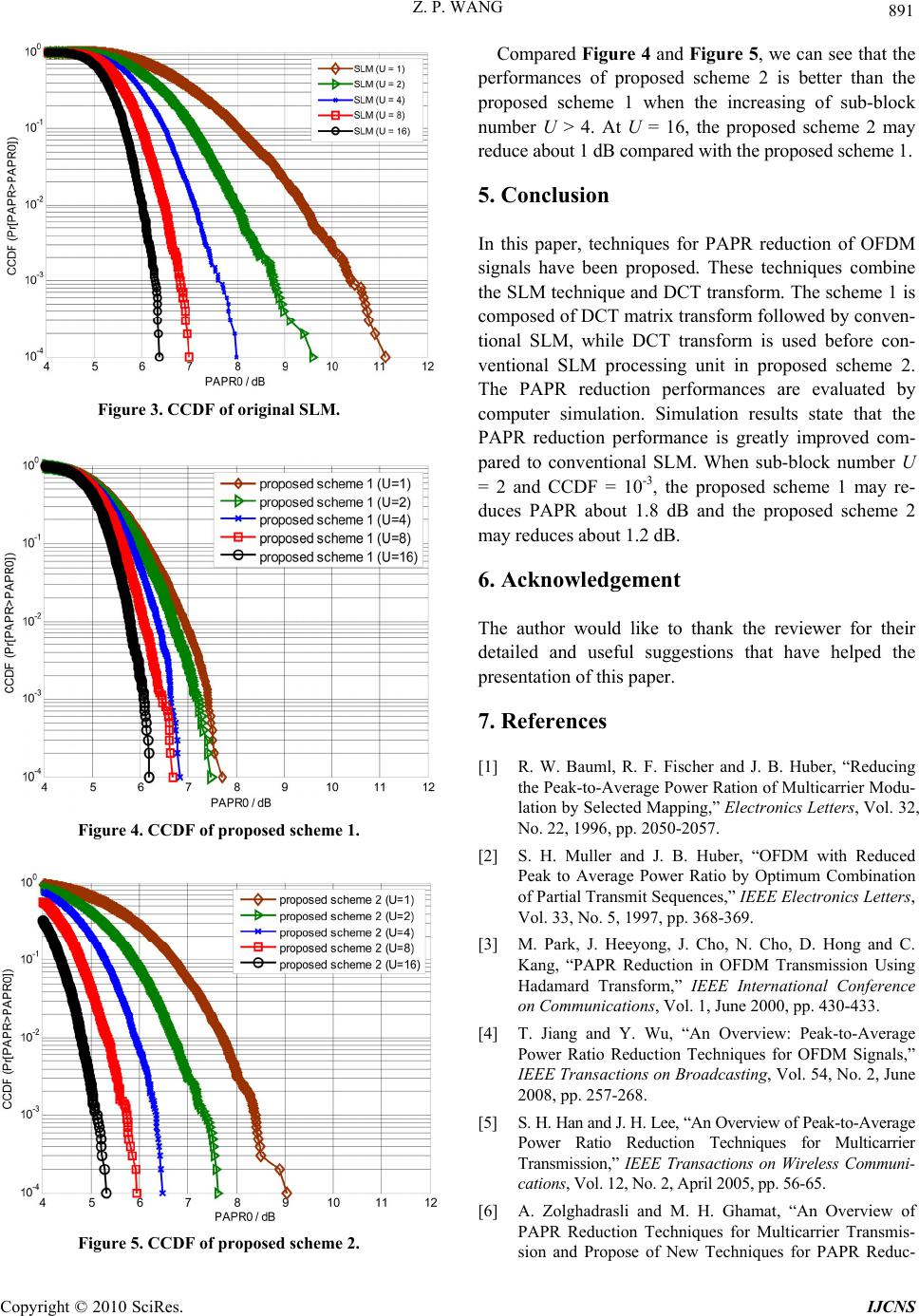

Z. P. WANG
891
Figure 3. CCDF of original SLM.
Figure 4. CCDF of proposed scheme 1.
Figure 5. CCDF of proposed scheme 2.
Compared Figure 4 and Figure 5, we can see that the
performances of proposed scheme 2 is better than the
proposed scheme 1 when the increasing of sub-block
number U > 4. At U = 16, the proposed scheme 2 may
reduce about 1 dB compared with the proposed scheme 1.
5. Conclusion
In this paper, techniques for PAPR reduction of OFDM
signals have been proposed. These techniques combine
the SLM technique and DCT transform. The scheme 1 is
composed of DCT matrix transform followed by con ven-
tional SLM, while DCT transform is used before con-
ventional SLM processing unit in proposed scheme 2.
The PAPR reduction performances are evaluated by
computer simulation. Simulation results state that the
PAPR reduction performance is greatly improved com-
pared to conventional SLM. When sub-block number U
= 2 and CCDF = 10-3, the proposed scheme 1 may re-
duces PAPR about 1.8 dB and the proposed scheme 2
may reduces about 1.2 dB.
6. Acknowledgement
The author would like to thank the reviewer for their
detailed and useful suggestions that have helped the
presentation of this paper.
7. References
[1] R. W. Bauml, R. F. Fischer and J. B. Huber, “Reducing
the Peak-to-Average Power Ration of Multicarrier Modu-
lation by Selected Mapping,” Electronics Letters, Vol. 32,
No. 22, 1996, pp. 2050-2057.
[2] S. H. Muller and J. B. Huber, “OFDM with Reduced
Peak to Average Power Ratio by Optimum Combination
of Partial Transmit Sequences,” IEEE Electronics Letters,
Vol. 33, No. 5, 1997, pp. 368-369.
[3] M. Park, J. Heeyong, J. Cho, N. Cho, D. Hong and C.
Kang, “PAPR Reduction in OFDM Transmission Using
Hadamard Transform,” IEEE International Conference
on Communications, Vol. 1, June 2000, pp. 430-433.
[4] T. Jiang and Y. Wu, “An Overview: Peak-to-Average
Power Ratio Reduction Techniques for OFDM Signals,”
IEEE Transactions on Broadcasting, Vol. 54, No. 2, June
2008, pp. 257-268.
[5] S. H. Han and J. H. Lee, “An Overview of Peak-to-Average
Power Ratio Reduction Techniques for Multicarrier
Transmission,” IEEE Transactions on Wireless Communi-
cations, Vol. 12, No. 2, April 2005, pp. 56-65.
[6] A. Zolghadrasli and M. H. Ghamat, “An Overview of
PAPR Reduction Techniques for Multicarrier Transmis-
sion and Propose of New Techniques for PAPR Reduc-

892 Z. P. WANG
tion,” Iranian Journal of Electrical and Computer Engi-
neering, Vol. 7, No. 2, Summer-Fall 2008, pp. 115-120.
[7] N. V. Irukulapati, V. K. Chaka and A. Jain, “SLM Based
PAPR Reduction of OFDM Signal Using New Phase Se-
quence,” Electronics Letters, Vol. 45, No. 24, 2009, pp.
1231-1232.
[8] N. T. Ahmed, Natarajan and K. R. Rao, “Discrete
Consine Transform,” IEEE Transactions on Computer,
Vol. 23, 1974, pp. 90-93.