Paper Menu >>
Journal Menu >>
 Int. J. Communications, Network and System Sciences, 2010, 3, 843-849 doi:10.4236/ijcns.2010.311114 Published O nline Novem ber 2010 (http:// www.SciRP.org/journal/ijcns) Copyright © 2010 SciRes. IJCNS Power Spectral Analysis of Orthogonal Pulse-Based TH-UWB Signals Sudhan Majhi, Paul Richardson Electrical and Computer Engineering, University of Michigan, Dearborn, USA E-mail: sudhanmajhi@gmail.com, richarpc@umd.umich.edu Received April 28, 2010; revised July 8, 2010; accepted September 10, 2010 Abstract The paper analyzes power spectral density (PSD) of orthogonal pulse-based signals for time hopping ultra wideband (TH-UWB) systems. Our extensive studies show that the PSD of these signals depends not only on the time dithering code and the modulation schemes, but also on the energy spectral density (ESD) of or- thogonal pulses. The different order orthogonal pulses provide different ESD which changes the shape of continuous spectral component with symbols. We show that orthogonal pulse-based signals reduce the dy- namic range of amplitude of discrete spectral components. Further, we reduce the dynamic range by adopting longer TH code over orthogonal pulse-based signals. As a result, UWB system performance improves with average transmitted power. The theoretical analysis of PSD of orthogonal pulse-based TH-UWB signal is provided in details and verified through simulation results. Keywords: Time Hopping Ultra Wideband Radio, Orthogonal Pulse Modulation, Power Spectral Density 1. Introduction Impulse radio Ultra Wideband (IR-UWB) radio is a promising technology for short range wireless commu- nications. The information is conveyed by short-duration pulse, which has potential to deliver high data rates with low power spectral densities (PSD). Federal Communi- cation Commission (FCC) has limited the PSD of the signal to –41.25 dBm/MHz in the band from 3.1 GHz to 10.6 GHz. However, the UWB signal interferes with other radio signals due to its noise like signal character- istic. The power distribution of UWB signal over a large bandwidth can be id entified by analyzing the PSD of the signal. The reduction of PSD of UWB signal reduces UWB interference on narrowband (NB) systems and keeps UWB signal under the FCC spectral mask [1]. Recently, orthogonal pulses have taken a lot of atten- tion in time hopping UWB (TH-UWB) systems [2]. Sev- eral modulation schemes such as pulse shape modulation (PSM), combined on-off -keying (OOK) and PSM, called OOK-PSM, combined PSM and pulse position modula- tion (PPM), called PSM-PPM, combined orthogonal PPM (OPPM) and bi-orthogonal PSM (BPSM), called OPPM-BPSM, have been proposed to simplify the TH-UWB systems [3-5]. The orthogonal pulse-based modulation schemes are becoming more popular due to the simplicity of newly developed pulse designed algo- rithms [6,7]. Th e efficiency of these orthogonal pulses is studied in [8,9]. The spectral characteristic of these or- thogonal pulses is provided in [10]. However, only few papers described the PSD of orthogonal pulse-based modulation schemes. In this paper, we analyze the power spectral de nsity of orthogonal pulse-based TH-UWB signal for PSM, BPSM, OPPM-PSM and OPPM-BPSM schemes. We show that orthogonal pulse-based modulation schemes adjust the continuous power spectrum component with FCC limita- tion and reduce the dynamic range of the amplitude of the discrete spectral components. Again we smooth the PSD of the signal by employing longer TH code over the orthogonal pulse-based modulation. The simulation re- sults are provided for PSD of TH-UWB signal for OPPM and OPPM-PSM schemes based on modified Hermite pulses (MHPs). The rest of the paper is organized as follows. Section 2 discusses a generalized orthogonal pulse-based TH-UWB signal. Section 3 presents derivation of PSD of orthogo- nal pulse-based TH-UWB signal. Section 4 characterizes PSD of TH-UWB signal for PSM, BPSM and OPPM- BPSM schemes. In Section 5, simulation results and discussion are provided. Finally, conclusion is drawn in Section 6.  844 S. MAJHI ET AL. 2. Generalized Orthogonal Pulse-Based UWB Signal Model In M-ary PSM scheme, different symbols are transmitted by different order orthogonal pulses. It requires M or- thogonal pulses at the transmitter and M correlators at the receiver. In M-ary BPSM scheme, symbols are transmit- ted by using positive or negative amplitude of the or- thogonal pulses. It requires orthogonal pulses at the transmitter and correlators at the receiver to transmit and receive all M possible symbols. In OPPM- BPSM scheme, M symbols are transmitted by using L pulse positions and N biorthogonal pulses where /2M /2M k M 2= , and [5]. l L2= 1 2lk =N OPPM-BPSM is a generalized modulation scheme of PSM, BPSM, OPPM-PSM and OPPM-PSM scheme [5]. By changing the number of pulse positions and orthogo- nal pulses, one can construct a wide variety of modulai- tons. For example, M-ary PSM scheme can be designed by using one pulse position and M orthogonal pulses whereas an M-ary BPSM can be constructed by using one pulse position and biorthogonal pulses. M-ary OPPM-PSM can be constructed by using L positions and 2N orthogonal pulses. /2M Since PSM, BPSM and OPPM-PSM are particular cases of OPPM-BPSM, only OPPM-BPSM signal model is provided. The M-ary OPPM-BPSM signal for user is given as thk )(=)( )()()()( k lc k jf k nmtx j k mnl TcjTtwdEts (1) where j is the index of time frame, Etx is the transmitted energy of the signal and {1} m d 0n f}{)(k j c <0 )( k jNc 1= m d 1/2, M , is the amplitude of pulse , n represents the order of the orthogonal pulse. The pulses have finite energy and are normalized to ensure equal energy per transmission, that is where . The pulse repetition interval Tf is divided into N h time slots of length Tc, where , is a pseudorandom TH code sequence, and . is the additional time shift from nominal position. For PSM scheme, , and . For BPSM scheme, , 1,2)=(m 1M 1 )(k l 0= )(k l 1= )( )( tw k n 1 chTTN 1, M 0,1,=n =|)(| 2dttwn 0,1,=n h m d n0,1,= and . For OPPM-PSM scheme, , and 0= )k 1= m ( l d N, 12 <<<< L f T where 0= 1 . For OPPM-BPSM scheme, 1= m d and other terms are same as OPPM-PSM. 3. Power Spectral Density Analysis In orthogonal pulse based signal, different symbols are transmitted by different order orthogonal pulses. The continuous spectrum, energy spectral density (ESD), changes with symbol. The discrete spectral component changes with orthogonality of the pulses and TH code. Therefore, a mathematical frame work is essential to understand the orthogonal pulse based PSD in the pres- ence of deterministic TH code. We assume that the analysis is only for 1 user. For simplicity, the super- script/subscript terms in (1) are omitted/modified. After some modification, sum of M symbol can be written from (1) as )(=)(, 1 0= 1 0= lchlffpll s N h M l pTchTTlNtwats (2) where l is the amplitude and l a is the pulse position. The terms l, l a and l are independent and sta- tionary process. The index is related to TH code, hl , and TH period, p. To simplify the analysis of the PSD of TH-UWB signal, it is assumed that the number of time frames for a symbol is s and it is equal to p. Since (2) depends on the time dithering, it can be written in continuous form as wp c, N N N ).(=)( fpp l TlNtsty (3) The PSD is computed by evaluating the Fourier trans- form (FT) of the autocorrelation function of , i.e., )(ty )()(=)( tytyEfPy (4) where denotes the FT and denotes the expectation operator. Therefore, the PSD can be ex- pressed as [11]. {.}{.}E )( )()( )( 1 )()( |)(| 1 =)( * 2 *2 fp qp k fp qpp fp y TN k ffSfSE TN fSfSEfSE TN fP (5) where and are two independent random vari- ables with the same probability distribution function. is the FT of . It can be expressed as p q )(fSp)(tsp l fj lll M l peafTfWfS 2 1 0= )()(=)( (6) where is the FT of the transmitted pulse . The time domain representation of (2 order MHPs can be expressed as )( fWl)(twl h)tl )(1)2()(2=)( 12twlttwtnw lll (7) The FT of can be expressed as )( 1fwl )](2)( 4 1 [=)( 1fWffWjfW lll (8) where “ · ” stands for derivative with respect to fre- Copyright © 2010 SciRes. IJCNS  S. MAJHI ET AL. 845 quency. For M HP, is defined as )( 0fW 22 4 02=)( f efW (9) The time and frequency domain representation of MHPs are given in Figure 1. )(fTl th is the FT of the TH code which transmits the symbol l .=)( )( , 2 1 0= f Th p lN c T hl cfj s N h lefT (10) To find the closed form expression of in (5), the expectation of is to be evaluated. It is given as )( fPy 2 |)(| fSp }.)( )()()( {=|)(| 2 * * 1 0= 1 0= 2 nl fj nln lnl M n M l p eaafT fTfWfWEfSE (11) Since l and n are independent random variables derived from the same process and l a a and n are in- dependent random variables derived from different processes. Therefore, (11) can be rewritten as }}.{}{}{ )()()()( }{|)(||)({|=|)(| )(2 ** 1 0= 222 1 0= 2 nl fj nl nlnl M nln lll M l p eEaEaE fTfTfWfW aEfTfWfSE (12) Similarly, the second expectation in (5) can be ex- pressed as Figure 1. Time and frequency (logarithmic plot) domains representation of modified Hermite pulses (MHPs). 11 ** =0 =02 {()()}= () ()()() }{ . MM pql nln ln jfln ln ESfSfWfWfT fTf EaEaE e * (13) The waveforms and are generated by two i.i.d processes. Therefore, the expectation in (13) is independent of and and equal to the case )(tsp n )(tsq l nl of (12), i.e., )()()()( }{}{}{=)}()({ ** 1 0= 1 0= )(2 * fTfTfWfW eEaEaEfSfSE nlnl M n M l nl fj nlqp (14) Substituting (12) and (14) in (5), the final PSD can be formulated as in (15). )()()()()( )}({}{}{ |)(||)(| }{}{}{}{=)( ** 1 0= 1 0= 2 )(2 22 1 0= )(2 2 fp k nlnl M n M l fp nl fj nl ll M l fp nl fj nlly TkNffTfTfWfW TNeEaEaE fTfW TNeEaEaEaEfP (15) 4. Characterization of PSD of TH-UWB Signal Although UWB signals are alike in the frequency do- main, they are diverse in the time domain due to their different characteristics of time domain parameters p, f, l and l. We see that the PSD of orthogonal pulse-based modulation signals consists of continuous and discrete spectral components which change with the order of pulse waveforms and modulation schemes. The variations of PSD over different orthogonal pulse-based signaling are given in the following subsection. N T aw 4.1. PSD of M-ary Pulse Shape Modulation (PSM) In PSM scheme, symbols are modulated only by the or- der of orthogonal pulses. The generalized terms in (15) are specified by l = 1 and a0= l . The expectations of these variables are , nlnl and respectively. The PSD of the PSM signal can be written from (15) as 1 {aE=}{ 2 l aE 0=}{} aE 1=}{ )(2 nl fj eE )()(=)( fpfpfP ky (16) where 22 1 0= |)(||)(|1=)( fTfWTNfp ll M l fp (17) and Copyright © 2010 SciRes. IJCNS  846 S. MAJHI ET AL. )( )()()()()1(=)(** 1 0= 1 0= 2 fp k nlnl M n M l fpk TkNf fTfTfWfWTNfp (18) We see that is continuous spectrum component. It depends on the TH code and the ESD of the or- der orthogonal pulse. Since ESD of different order or- thogonal pulses are not identical, the selectio n of order of the orthogonal pulses plays an important role for con- tinuous spectral component. )( fp thl )( fpk is the discrete spectral components which in- duces UWB interference on the other narrow band sys- tems [12]. The discrete components of the signal appear based on the term . It shows that the position of discrete component depends on the TH code and its dynamic range of amplitude depends on the or- thogonality of pu lses. Since pulses are or thogon al in time and frequency domains, the value of is approximately zero, as a result, the dynamic range of amplitude of the discrete spectral components becomes very small. This small dynamic range increases the av- erage transmitted power in pulse and improves the UW B system performance. It helps UWB signal to coexist with other systems without any serious performance degrada- tion. In addition, it facilitates UWB signal to keep its spectrum under the FCC spectral mask without mini- mizing the averag e transmitte d power in the signal. )( fp kTkNf )()( *fWfW nl 4.2. PSD of M-ary Biorthogonal PSM (BPSM) In BPSM scheme, symbols are modulated by order and amplitude of the pulses, i.e., and 1}{ l a0= l . The expectation of these variables are , 1=} 2 ) {l aE (2 fj 0=}{}{ nlnl aEaE and . 1=}{ nl eE The corresponding PSD of BPSM scheme can be ex- pressed from (15) as ))()((2exp |)(|1=)( ,, 2 1 0= 1 0= 1 0= fcklhl l s N k s N h M l fpy TkhTccfj fWTNfP (19) The continuous PSD component of BPSM signal is same as PSM scheme. However, the discrete spectral components become zero due to the antipodal pulse. The PSD of the TH-UWB signal for BPSM scheme is smoothed. This allows the signal to coexist with other NB signals. The extensive studies found that any antipo- dal signal has only continuous spectral component [12]. The continuous component can be easily fitted to FCC by using appropriate MHPs. 4.3. PSD of M-ary OPPM-BPSM For OPPM-BPSM scheme, and 1}{ l a 1)(= l l, where is the constant time shift length. This implies, , and 1{ 2 l aE =} 0=}{nlaaE 2fmTj ))/2(2cos(1=}{ TmfeE . The corresponding PSD of OPPM-BPSM signal can be expressed as ))()((2exp |)(|1=)( ,, 2 1 0= 1 0= 1 0= fcklhl l s N k s N h M l fpy TkhTccfj fWTNfP (20) The PSDs of BPSM and OPPM-BPSM schemes are identical. However, OPPM-BPSM can be used for higher level modulation scheme for higher data rate systems. Therefore, OPPM-BPSM modulation is an attractive choice of TH-UWB signal from several aspects. 5. Simulation Results and Discussions In this section, PSD is provided for orthogonal pulse- based signaling and compared with conventional OPPM scheme. In simulation, different orders of MHPs are used with two different lengths of TH code 8 and 16. The other simulation parameters are set to ns and pulse width is 7 ns. 60= f T Since BPSM and OPPM-BPSM have antipodal signal, they have only continuous spectral component and shape of their spectral is same as continuous component of non antipodal signal. The only difference is that the spectral of antipodal signal does not contain any discrete compo- nent. The PSD in non antipodal modulation schemes is more complicated. Since OPPM and OPPM-PSM are special cases of OPPM-BPSM, OPPM and OPPM-PSM have been chosen to compare the PSD of the signal. The PSD of 8-ary OPPM is given in Figure 2 for order pulse and in Figure 3 for and order pulses with TH code of length 8 and . Since each time only one pulse is used in OPPM scheme, orthogonality is maintained by position not by pulse. The 3r order pulse almost satisfies the FCC spectral mask except some discrete components. However, and order pulses do not satisf y the FCC spectral mask shown in Figure 3. The dynamic range of the amplitude of dis- crete components of OPPM scheme is about 8 dB which is very high. The power of the signal is calculated based on the line where the dynamic range is zero (4 dB bellow from the pick point). As FCC rules, pick amplitude must be bellow the –41.25 dBm limit. Therefore, the power of the signal is calculated based on the line which is maxi- mized up to –45.25 dBm. As a result, signal provides low average transmitted power which degrades the system 3rd d 4th c T5th 4t 7.5= h5th Copyright © 2010 SciRes. IJCNS  S. MAJHI ET AL. Copyright © 2010 SciRes. IJCNS 847 Figure 2. PSD of 8-ary OPPM scheme with 3rd order MHP and TH code length is 8. Figure 3. (a) PSD of 8-ary OPPM scheme with 4th order MHP; (b) PSD of 8-ary OPPM scheme with 5th order MHP and TH code length is 8. 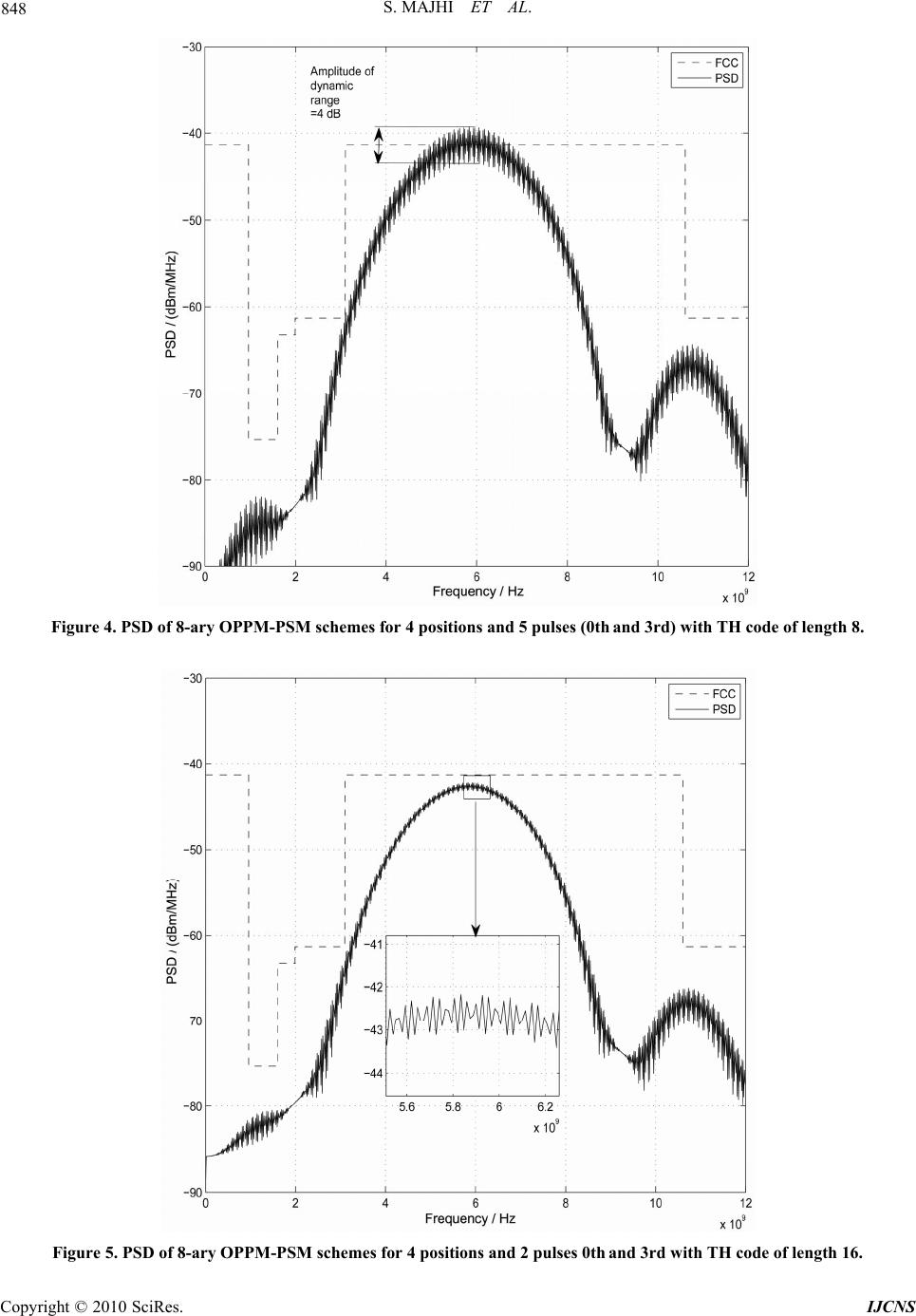 848 S. MAJHI ET AL. Figure 4. PSD of 8-ary OPPM-PSM schemes for 4 positions and 5 pulses (0th and 3rd) w i th TH code of length 8. Figure 5. PSD of 8-ary OPPM-PSM schemes for 4 positions and 2 pulses 0th and 3rd with TH code of length 16. Copyright © 2010 SciRes. IJCNS  S. MAJHI ET AL. Copyright © 2010 SciRes. IJCNS 849 performance. Not that if the dynamic range becomes zero, the maximum limit becomes –41.25 dBm. Figure 4 shows the PSD of 8-ary OPPM-PSM for 4 positions and 2 orthogonal pulses with TH code of length 8. We see that that dynamic range of the amplitude of the discrete spectral component of OPPM-PSM scheme is 4 dB which is lesser than the OPPM scheme even the same length of TH code is used. It is because of the orthogo- nality of pulses. So by reducing dynamic range, we can improve the UWB system performance by increasing the average transmitted power in the signal pulse as well as we can reduce the UWB interference over other radio systems. Again by applying TH code over these or- thogonal pulse-based modulations, dynamic range of amplitude of discrete component further could be re- duced. Figure 5 shows the PSD of 8-ary OPPM-PSM with TH code of length 16 and . The dynamic range is almost reduced to 1 dB. However, it can not be reduced to zero whatever the length of TH code used. We also see that the average transmitted power in Figure 5 is more than the previous cases. Therefore, orthogonal pulse-based TH-UWB signaling has several advantages than its complexity burden. 3.75= c T 6. Conclusion PSD of orthogonal pulse-based TH-UWB signal has been analyzed based on stochastic signal theory. This shows that the continuous and discrete components change with order of pulses and modulation schemes. The discrete component can be removed by employing an antipodal signal. If the signal is not antipodal, the dy- namic range of amplitude of the discrete component can be reduced by using orthogonal pulse-based modulation and long TH code. Therefore, it has been proved that the orthogonal pulse-based signaling not only reduce the dynamic range of discrete spectral component also im- prove the system performance by increasing the average transmitted power in the signal. 7. References [1] S. Majhi, A. S. Madhukumar and A. B. Premkumar, “Reduction of UWB Interference at NB Systems Based on a Generalized Pulse Waveform,” IEICE Electronics Express, Vol. 3, 2006, pp. 361-367. [2] W. Lee and S. Jitapunkul, “Orthogonal Pulse Design for UWB Systems with Timing Jitter,” International Con- ference on Advanced Communication Technology, Phoenix, February 2009, pp. 22-27. [3] A. B. P. Sudhan Majhi, A. S. Madhukumar and P. Richardson, “Combining OOK with PSM Modulation for TH-UWB Radio Systems: A Performance Analysis,” EURASIP Journal on Wireless Communications and Networking, Vol. 2008, 2008. [4] C. Michell, G. T. F. de Abreu and R. Kohno, “Combined Pulse Shape and Pulse Position Modulation for High Data Rate Transmission in Ultra-Wideband Communication,” International Journal of Wireless Information Networks, Vol. 10, October 2003, pp. 167-178. [5] S. Majhi, A. S. Madhukumar, A. B. Premkumar and F. Chin, “M-ary Signaling for Ultra Wideband Communica- tion Systems Based on Pulse Position and Orthogonal Pulse Shape Modulation,” IEEE Wireless Communication and Networking Conference (WCNC), March 2007, pp. 2795-2799. [6] I. Dotlic and R. Kohno, “Design of the Family of Or- thogonal and Spectrally Efficient Uwb Waveforms,” IEEE Journal of Selected Topic in Signal Processing, Vol. 1, No. 1, June 2007, pp.21-30. [7] Y. Chen, E. Gunawan, K. S. Low, S. Wang, Y. Kim and C. B. Soh, “Pulse Design for Time Reversal Method as Applied to Ultrawideband Microwave Breast Cancer De- tection: A Two-Dimensional Analysis,” IEEE Transac- tions on Antennas and Propagation, Vol. 55, No.1, Janu- ary 2007, pp. 194-204. [8] Y. Kim and F. B. Womack, “Performance Evaluation of UWB Systems Exploiting Orthonormal Pulses,” IEEE Transactions on Communications, Vol. 55, No. 5, May 2007, pp. 929-935. [9] J. H. Hwang, S. C. Kim, B. K. S. Yoon and J. S. Park, “Performance Analysis of PO-THMA UWB System Us- ing Mutually Orthogonal MHP Pulses,” IEEE Transac- tions on Consumer Electronics, Vol. 53, No. 1, February 2007. pp. 39-45. [10] J. A. N. da Silva and M. L. R. de Campos, “Spectrally Efficient UWB Pulse Shaping with Application in Or- thogonal PSM,” IEEE Transactions on Communications, Vol. 55, No. 2, 2007, pp. 313-322. [11] J . E. Padgett, J. C. Koshy and A. A. Triolo, “Physi- cal-Layer Modeling of UWB Interference,” White Paper of Telcordia Technologies, January 2003, pp. 1-121. [12] S. Majhi, A. S. Madhukumar and Z. Ye, “Coexisting Narrowband and Ultra Wideband Systems: Analysis of Power Spectral Density and In-Band Interference Power,” WSEAS Transaction on Communication, Vol. 6, February 2007, pp. 118-124. |

