Circuits and Systems
Vol.07 No.06(2016), Article ID:66625,15 pages
10.4236/cs.2016.76081
A Process Variation Tolerant OTA Design for Low Power ASIC Design
R. Benschwartz, P. Sakthivel
Department of Electronics and Communication Engineering, College of Engineering Guindy, Anna University, Chennai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 April 2016; accepted 17 May 2016; published 20 May 2016
ABSTRACT
Technology development and continuous down scaling in CMOS fabrication makes Mixed Signal Integrated Circuits (MSIC) more vulnerable to process variation. This paper presents a well defined novel design methodology for process variability aware design by incorporating the major challenge of statistical circuit performance relating the device and circuit level variation in an accurate and efficient manner to improve the reliability, robustness and stability of the circuit. The device sensitive parameters are identified and accurately quantified by continuous realistic assessments using statistical methods. The modularity of the methodology can be validated by the output performance obtained from the gain and phase response of OTA which is highly stable when subjected to worst case process variation scenario. In the proposed optimization, the circuit is strengthened by fixing the optimum aspect ratio without adding any additional compensation devices complicating the circuit resulting in low power consumption of only 0.116 mW in standard CMOS 0.18 µm technology with 1.8 V power supply.
Keywords:
MSIC, Process Voltage Temperature, Operational Transconductance Amplifier, Monte Carlo Simulation

1. Introduction
Large demand of high performance CMOS mixed signal systems requires stable output performance independent of power supply, process and temperature variations. With the technology development and supply voltage reduction impact of process variation, parameters are more dominant in low power battery operated electronic systems. Highly accurate and high precision stable OTA driving large capacitive loads are used as error amplifiers in low-voltage low-drop-out (LDO) regulators [1] - [3] . Due to constraints on the minimization of design time and die area/cost, efficient circuit developments with design reuse and/or technology migration methodologies have been developed for principle analog blocks, such as operational transconductance amplifiers (OTAs), com- parators, LNAs and so on [4] . Despite its popularity, only uncompleted design procedures were proposed for this OTA which arbitrarily reduced the degree of freedom in the design equations, hence precluding the possibility to meet optimized performance. Indeed, the approach proposed in [5] sets arbitrarily the compensation capacitor equal to the load capacitor, and that presented in [6] introduces constraints that require an onerous recursive procedure. With the scaling down of device sizes and supply voltages, single-stage cascode or telescopic amplifiers are not suitable for high-gain wide-bandwidth amplifiers. A low-power low-area and frequency-com- pensated multistage amplifier capable of driving large capacitive loads is a necessity. OTA [7] - [12] required a robust frequency compensation scheme due to their potential closed-loop stability problems. In an OTA, the ratio of transconductance to current consumption reflects the power efficiency. In order to obtain lower power, the efficiency of the OTA must be improved. In addition with the scaling of the supply voltages, the reduction of the threshold voltage is not aggressive, which limits signal swings. In recent years, the process variation parameters of the MOSFET have become a dominant cause in variation affecting the stability of the circuit. Therefore, OTAs generate large distortion when produced by the present manufacturing process. Many design methodologies have been developed to optimize the design of OTA’s. In this paper, a new methodology is adopted to design the OTA and hence satisfies the state of art design specification.
2. Challenges in Statistical Optimized Design Methodology
The major challenge of statistical circuit performance analysis is how to relate the device-level variation to the circuit-level variation in an accurate and efficient manner. Two conventional approaches for simulating the impact of device variation on circuit performance are as follows: 1) corner-model method and 2) Monte Carlo (MC) SPICE simulation [14] . The corner method is simple, computationally efficient, and thus widely adopted by circuit designers. However, the corner approach usually gives overly pessimistic or optimistic performance prediction due to insufficient attention to the quantitative correlations between the corner models and the circuit performance variations. The MC SPICE provides more accurate prediction using statistical information but is computationally expensive for complex VLSI circuits. In addition, the accuracy of the MC approach depends on the accuracy of the variations of the SPICE model parameters. The latter accuracy can be improved with greater attention paid to the ET variation data [15] . Principal component analysis (PCA) was introduced to capture the complex correlations of device parameters [16] . PCA transforms the correlated device parameters into uncorrelated variable (principal component). Each device parameter is a linear or nonlinear combination of the principal components. There is no physical interpretation of these principal components. However, the accuracy of PCA can be problematic in nanoscale CMOS technology due to highly nonlinear device characteristics and heterogeneity of device parameter [17] . To overcome this issue, an ET-based direct sampling methodology (DSM) extracts device model parameters for all test sites and preserves the existing complex nature of parameter correlations [17] [18] . DSM can predict more accurate distribution of circuit performance due to stochastic process variations. However, the accuracy of the DSM relies on the number of generated device parameter sets. The more generated parameter sets lead to more accurate predicted results. The efficiency of the device parameter extraction for significant number of test sites could be problematic due to a more complex process introduced in the advanced CMOS technology. Backward propagation of variance approach was introduced to model the process variations based on physical process parameters and the propagation of the variance. The model is efficient and general for all kinds of variability studies. However, the model requires a very accurate nominal SPICE model card with correct sensitivities to different process parameters. In addition, the model does not account for nonlinearities of the sensitivity, which could lead to inaccurate results when variations are large. The improved set of model parameter variations will directly improve the accuracy of MC circuit simulations. Furthermore this paper proposes a systematic optimized methodology that correlates the corner model approach and montecarlo simulation. This paper presents a methodology to develop a variability aware computationally compact parameter set for the parameters that impact on the sensitivity of the device parameter.
3. The Principle of Approach
Process variations can be incorporated in the design of OTA by considering the worst case condition as shown in Table 1 under a desired level of confidence. Instead of choosing a minimal or the nominal value, optimal
Table 1. Worst case corner conditions for typical, slow and fast transistors [M5].
values have to be chosen by incorporating various methodologies. In this paper an OTA is designed considering the process sensitive parameter in the design. The proposed optimization design flow is shown in Figure 1. The optimal value of the process sensitive parameter is chosen such that the values are not allowed to be greater than the worst case value (i.e. the degradation in performance is allowed to be greater than the maximum acceptable). For simplicity threshold voltage variation and drain current variation is described in this paper. Initially to model circuit process variability is modeled by worst case corner models for OTA as shown in Table 1 are generated from slow nMOS and slow pMOS (SS) to model the worst-case delay (WS), and from fast nMOS and fast pMOS (FF) to model the worst-case power (WP); whereas, the corner models for digital applications are generated from fast nMOS and slow pMOS (FS) to model the worst-case “1”, (WO) and from slow nMOS and fast pMOS (SF) to model the worst-case “0” (WZ). A standard set of model parameters {e.g. Vth, W, L, Tox, µeff, γ, Rbs, Cov, Cj} is used to account for process variability and model the worst-case corner performance of devices and circuits.
Threshold Voltage Mismatch (VTH)
The threshold voltage Vth is mainly determined by process variation dependent sensitive parameters {Vth, W, L, Tox, µeff, γ, Rbs, Cov, Cj}, whose effect strongly dominates over the intrinsic imbalance at nominal conditions. This clearly shows that variations are very critical in ULP/ULV mixed signal standard CMOS circuits. Since the performance of the device changes drastically with PVT associated parameters. To model the threshold voltage Vth, the standard deviation (σ) limits are preset to include any process variability over a wide range. The worst case corner models are generated by offsetting the selected compact model parameter (P) of the typical (TT) compact model by ±dp = nσ to account for a window of process variability, where n is the number of σ for P so that it is selected to set the upper and lower limits. The corner models of BSIM4 TT model parameter Vth0 is defined as
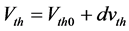 (1)
(1)
where 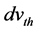 is used to set the fixed UL and LL of the models. The variation of threshold voltage ∆Vth due to global and local mismatch is calculated and the variance
is used to set the fixed UL and LL of the models. The variation of threshold voltage ∆Vth due to global and local mismatch is calculated and the variance 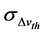 is determined.
is determined.
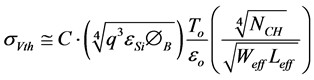 (2)
(2)
where C is a constant and is given by 0.8165 [19] or 0.7071 [20] with or without the dopant variation along the depth of the channel region, respectively; q is the electronic charge, εSi and εox are the permittivity of silicon and
silicon-dioxide (SiO2), respectively; 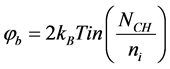 is the bulk potential of the channel region of MOS-
is the bulk potential of the channel region of MOS-
FETs with kB, T, and ni are the Boltzmann constant, absolute temperature, and intrinsic carrier concentration, respectively. Weff and Leff represent the effective dimension of W and L, respectively. The impact of vth on device scaling as shown in Figure 2.
Figure 1. Proposed design optimization flow for OTA considering Worst case (PVT) scenario.
Figure 2. Estimated Vth variation for variation in width W = 3.25 µm and 4.2 µm.
Normal distribution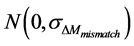 , where
, where 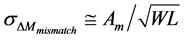 [20] - [22] .
[20] - [22] . 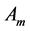 is the technology depen- dent constant of ∆M. Thus for threshold voltage model Vth0, the variance of
is the technology depen- dent constant of ∆M. Thus for threshold voltage model Vth0, the variance of  between two transistor is given by
between two transistor is given by , where
, where 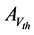 is an area dependant constant of
is an area dependant constant of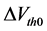 , depends on ∆XW, ∆XL, ∆Tox, ∆U0 and ∆K1. Now for a single device we get
, depends on ∆XW, ∆XL, ∆Tox, ∆U0 and ∆K1. Now for a single device we get

where 



Thus the model parameter M including both local and global process variability components is given by

Equation (5) is the generalized compact model of the target technology for process variability aware analysis. Thus for compact model parameter Vth is given by

This Equation (6) is used to build a statistical corner model for threshold voltage Vth realistic analysis of process variability. Similar method is adopted for all the sensitive parameters in the design. Montecarlo simulations are made for 200 runs and the histogram of Vth for M5 is shown in Figure 3. The mean and standard deviation of the parameter is observed, compared with the value and scattered plot is obtained as shown in Figure 4. The optimized value is validated with Equation (6) and optimized.
4. Proposed Optimized Ota Design Flow Considering the Worst Case Scenario
General methodology adopted for process variation insensitive design
1) Select transistor gate length from intrinsic gain plat, so that the designed OTA satisfies the required gain.
2) Determine the transconductance gm to realize the OTA’s required frequency response. Analytical expression for the transfer function and settling behavior must be derived for a specific topology.
Figure 3. Histogram for Vth variation representing the mean and standard deviation.
Figure 4. Scatter plot representing Gm and Vth over all corners.
3) Optimize gm/IDS to meet the required specification. Once gm/IDS (intrinsic gain) is determined, FT, Cgg and the associated parasitic capacitors can be obtained from the statistical variation sensitive model parameter lookup table developed.
4) Determine IDS from gm and gm/IDS.
5) The mismatch in the relative drain current △IDS/IDS is calculated. The variance of the relative drain current including global and local mismatch is derived.
6) Relative drain current mismatch △IDS/IDS is calculated by including the variation sensitive compact model parameter set {Vth0, W, L, Cox, µeff, γ, RDS, Cov, Cj}.
7) The process variability sensitive model parameter is included and optimized IDS is calculated.
8) Determine the transistor gate widths W from the calculated IDS and current density plot.
OTA Design Optimization Flow
1) Determine the value of the total capacitance including the global and local variability sensitive compact model parameter, with overlap capacitance Cov {CGSO, CGDO, CGSL AND CGDL}; {CJS, CJD} defining the source to drain junction area capacitance; and {CJSWS, CJSWD, CJSWGS, CJSWGD} defines the source to drain junction sidewall capacitance.
2) Determine the variance of the model parameter and add it to the mean value to analyze the change in value of the parameter.
3) Determine the gate length from the DC requirements and optimize gm/IDS for the output of the optimized OTA design.
4) Optimize the circuit parameters [Vth, W, L, Tox, µeff, γ, Rbs, Cov, Cj] of the OTA with an iteration loop until the variation in output is tolerable to the change in variation sensitive parameter.
5) Optimize the bias currents and fix the region of transistor to satisfy the reqired design specification.
6) Determine the gate width (Weff) of the transistor to be used in amplifier design.
7) Repeat the above process for each transistor in the design.
5. Design Approach
Generally the design of OTA can be divided into two distinct design related activities that are most port independent of one another. The tail current transistor for the differential amplifier will only consume voltage thus reducing the output swing. The first of these activities involves choosing or creating basic structure for the op-amp. Once the structure has been selected, the designer must select dc current and begin to size the transistors and design the compensating circuit. Most of the work involved in completing a design is the second activity of the design process. Note that the devices must be properly scaled in order to meet all the ac and dc requirements imposed on the top. Before designing the OTA one must sort out all the requirements and boundary conditions that will be required to guide the design flow.
5.1. Analysis and Design of DC Gain
The overall gain of the OTA is given by


where Av0 is the DC gain of the OTA, gm is the trans conductance of the MOS, r0 is the effective output impedance. The design procedure begins by choosing a device length to be used throughout the circuit. In general in designing analog circuit we normally avoid channel-length modulation. Therefore the chosen length











5.2. Tuning of Aspect Ratio
The aspect ratio of the transistor








If the value determined for 



If the value of 






For a phase margin 60˚, the location of the output pole was assumed to be placed at 2.2 times GB. Based on this assumption and the relationship for pole 2. The transconductance 



Knowing the 


Noting that one must now check to make sure ha the maximum output voltage specification is satisfied. Finally the device size of 


5.3. Small Signal Analysis of OTA
In analog circuit designs, the small signal model is widely used to analyze the behavior of analog circuits. To ensure the accuracy of the model, we must verify the small signal model with CMOS circuit. In order to achieve simplicity without losing of accuracy, the intrinsic part of complete small signal equivalent circuit of CMOS transistor, has been applied in the small signal model. The verification of the small signal model is illustrated by a CMOS two-stage OTA shown in Figure 1. The conventional small signal model of CMOS amplifier is widely used based on the hybrid-pi model of CMOS transistor shown in Figure 5. In the hybrid-pi model, the Gate- Source capacitor (Cgs) and Gate-Drain capacitor (Cgd) have not been considered. The capacitor Cgs can be neglected while the voltage VGS is an ideal voltage source. In the two stage OTA, the input voltage Vin connects to M1 and M2 is generally assumed to be the ideal voltage source in the small signal model. Thus, the Gate-Source capacitor of M1 can be ignored in the small signal model. The Gate-Drain capacitor Cgd1 of NMOS input differential pair M1 and M2 is connected to input voltage Vin and cannot be ignored.
The Gate-Source capacitor of M6, Cgs6, must be considered in the small signal model since VGS6 is not an ideal voltage source. The Gate-Drain capacitor of M6, Cgd6, is connected to the output node Vout. Thus, capacitor Cgd5 will affect the circuit performance of the two-stage OTA and cannot be ignored in the small signal model. The complete small signal equivalent circuit of CMOS transistor has been discussed in [6] . In order to achieve simplicity without losing of accuracy, the intrinsic part of complete small signal equivalent circuit of CMOS transistor, has been applied in the modified model. Therefore, the modified small signal model of the two-stage OTA can be obtained as shown in Figure 6. The modified model contains three parasitic capacitors Cgd1, Cgs5, and Cgd5 compared to the conventional model. In order to achieve simplicity without losing of accuracy, the intrinsic part of complete small signal equivalent circuit of CMOS transistor, has been applied in the small signal model. The nominal value of the parasitic capacitors Cgd1, Cgs6, and Cgd6, can be obtained from the SPICE simulations of the two stage OTA shown in Table 2.
Table 2. Optimized parameters of transistor.
Figure 5. Small signal model of OTA.
Figure 6. Schematic of OTA.
5.4. Miller Compensation Technique
This technique is applied by connecting a capacitor from the output to the input of the second transconductance
stage





complex frequency plane, resulting from the negative feedback reducing the output resistance of the second stage.
From the simplified model

The overall transfer function that results
From the standard second order system

where 



Since 





5.5. Phase Margin (PM)
This Phase Margin will define the stability of an amplifier. Higher value of PM will allow the output signal to achieve steady state without much ringing. Lower values will cause ringing at the output. The value of phase margin depends on the application. For most or well defined PM of 60˚ is needed


For stability of OTA the phase margin PM ≥ 60˚ then 






6. Simulation Results
The OTA is designed using conventional and proposed optimization methodology as shown in Figure 6 is designed and simulated in CADENCE spectre in 180nm CMOS technology. The supply voltage of the OTA is 1.8 V. The size of the transistors is optimized and the transistor parameter together with transconductance is shown in Table 3.
All significant variation sensitive process parameters are varied by the optimum percentage value from their nominal values and Monte Carlo simulations for the two-stage OTA and corner analysis is made with the variation range of each circuit parameter and results are obtained model can be obtained as shown in Table 4. The circuit parameters are varied up to its maximum allowable value from their nominal values. By consider the variation range of each circuit parameter, the performance bounds can be evaluated by the proposed approach. It is observed that the aspect ratios of the transistors are as minimum as possible demonstrating to give stabilized response as shown in Figure 7(c). Table 4 shows a summary of the performance parameters of OTA under typical conditions. The frequency and phase response of the OTA designed with conventional and proposed me-


Figure 7. Frequency response of OTA (a) Conventional design with W5 variation; (b) Conventional design with temperature variation; (c) Proposed design with W5 variation.
Table 3. Optimal value of small signal parameters obtained from montecarlo analysis 200 runs.
Table 4. Simulated performance of OTA with proposed design methodology.
thodology is shown in Figure 7. Simulated results show that the DC gain of the OTA with conventional methodology for a load of 2 pF and 5 pF is 64.11 dB and 66.43 respectively. The slewrate of the OTA is observed from the simulated response obtained from the step input as shown in Figure 8. Figure 9 shows the variation of gain and phase margin of the OTA with conventional and proposed design methodology with varying width (W µm), temperature representing PVT variations. It is observed that the frequency of the OTA designed with optimized methodology is more stable than the conventionally designed. The both the OTA is simulated for the worst case corner models with the constraints as shown in Table 1 and it is observed that the gain and phase variation more in conventionally designed OTA.
To study robustness to mismatch and process variations, montecarlo analysis with over 200 runs were performed. The results are shown in Table 1. Figure 9(a) shows the variation in gain for OTA with the conventional and proposed design methodology over all process corners. It is observed that the deviation in gain is more in conventionally designed OTA. Figure 9(c) shows the change in gain for the conventional and optimized OTA with varying loads. Figure 10 shows the layout of the optimized OTA is implemented in CADENCE 0.18 µm CMOS technology thus proving the enhancement in stability of the frequency responses even under worst case mismatches and process variations. Figure 11 depicts the comparative analysis of the power consumption by different OTA’s. Table 5 depicts the performance summary of conventionally designed OTA’s with the proposed design methodology.


Figure 8. Simulated response for step input for CL (a) 5 pF; (b) 2 pF.


Figure 9. Variation of gain in OTA for worst case process corners (a) Conventional design; (b) Proposed design; (c) Change in gain for OTA by both conventional and proposed designs.
Figure 10. Layout of the optimized OTA 180 nm CMOS technology.
Figure 11. Power comparison of proposed optimized OTA.
Table 5. Performance summary of the OTA and comparison with recently published work.
7. Conclusion
This paper presents a simple and efficient design methodology to stabilize the gain and phase margin of a conventional OTA in 180 nm CMOS process subjected to process variation. An efficient methodology to evaluate the performance of the circuit considering the PVT variations is modeled. By considering the worst case design scenarios in the design a combination of analytical and simulation based circuit optimization is performed. A significant improvement in stability of the device process sensitive parameters is observed in all stages in the design. From the comparative analysis, it is identified that the OTA designed by proposed optimized methodology consumes only 23 percent of the average power consumed by different other OTA’s designed by conventional methodology. The circuit simulation results confirm that the frequency response of OTA is more stabilized and this proves the superiority of the proposed design approach over all the conventional approach. From the performance metrics observed a series of comparison is made confirming the technical merits of reliability, robustness and performance enhanced characteristics using the proposed design approach.
Cite this paper
R. Benschwartz,P. Sakthivel, (2016) A Process Variation Tolerant OTA Design for Low Power ASIC Design. Circuits and Systems,07,956-970. doi: 10.4236/cs.2016.76081
References
- 1. Sánchez-Sinencio, E. and Andreou, A.G. (1999) Low-Voltage Low-Power Integrated Circuits and Systems. IEEE Press, New York.
- 2. Rincón-Mora, G.A. (2000) Active Capacitor Multiplier in Miller-Compensated Circuits. IEEE Journal of Solid-State Circuits, 35, 26-32.
http://dx.doi.org/10.1109/4.818917 - 3. Rincón-Mora, G.A. and Allen, P.E. (1998) A Low-Voltage, Low Quiescent Current, Low Drop-Out Regulator. IEEE Journal of Solid-State Circuits, 33, 36-44.
http://dx.doi.org/10.1109/4.654935 - 4. Gregorian, R. and Temes, G.C. (1986) Analog MOS Integrated Circuits for Signals Processing. John Wiley & Sons.
- 5. Allen, P. and Holberg, D. (1987) CMOS Analog Circuit Design. Holt Rinehart and Winston Inc.
- 6. Eschauzier, R.G.H., Kerklaan, L.P.T. and Huijsing, J.H. (1992) A 100-MHz 100-dB Operational Amplifier with Multipath Nested Miller Compensation Structure. IEEE Journal of Solid-State Circuits, 27, 1709-1717.
http://dx.doi.org/10.1109/4.173096 - 7. You, F., Embabi, S.H.K. and Sánchez-Sinencio, E. (1997) Multistage Amplifier Topologies with Nested G-C Compensation. IEEE Journal of Solid-State Circuits, 32, 2000-2011.
http://dx.doi.org/10.1109/4.643658 - 8. Leung, K.N. and Mok, P.K.T. (2001) Nested Miller Compensation in Low Power CMOS Design. IEEE Transactions on Circuits and Systems II, 48, 388-394.
http://dx.doi.org/10.1109/82.933799 - 9. Ng, H.T., Ziazadeh, R.M. and Allstot, D.J. (1999) A Multistage Amplifier Technique with Embedded Frequency Com- pensation. IEEE Journal of Solid-State Circuits, 34, 339-347.
http://dx.doi.org/10.1109/4.748185 - 10. Leung, K.N., Mok, P.K.T., Ki, W.-H. and Sin, J.K.O. (2000) Three Stage Large Capacitive Load Amplifier with Damping-Factor Control Frequency Compensation. IEEE Journal of Solid-State Circuits, 35, 221-230.
http://dx.doi.org/10.1109/4.823447 - 11. Thandri, B.K. and Silva-Martinez, J. (2003) A Robust Feed Forward Compensation Scheme for Multistage Operational Transconductance Amplifiers with No Miller Capacitors. IEEE Journal of Solid-State Circuits, 38, 237-243.
http://dx.doi.org/10.1109/JSSC.2002.807410 - 12. Lee, H. and Mok, P.K.T. (2003) Active-Feedback Frequency Compensation Technique for Low Power Multistage Amplifiers. IEEE Journal of Solid-State Circuits, 38, 511-520.
http://dx.doi.org/10.1109/JSSC.2002.808326 - 13. Zhao, X., Zhang, Q.S. and Deng, M. (2014) A 1-V Recycling Current OTA with Improved Gain-Bandwith and Input Output Range. IEICE Electronic Express, 11, 1-9.
- 14. Power, J., Donnellan, B., Mathewson, A. and Lane, W. (1994) Relating Statistical MOSFET Model Parameter Variabilitie’s to IC Manufacturing Process Fluctuations Enabling Realistic Worst Case Design. IEEE Transactions on Semiconductor Manufacturing, 7, 306-318.
http://dx.doi.org/10.1109/66.311334 - 15. Chen, J., Orshansky, M., Hu, C. and Wan, C.-P. (1998) Statistical Circuit Characterization for Deep-Submicron CMOS Designs. Proceedings of ISSCC, 90-91.
http://dx.doi.org/10.1109/isscc.1998.672388 - 16. Power, J.A., Mathewson, P.A. and Lane, W. (1993) An Approach for Relating Model Parameter Variabilities to Pro- cess Fluctuations. Proceedings of the 1993 International Conference on Microelectronic Test Structures, Barcelona, 22-25 March 1993, 63-68.
- 17. Orshansky, M., Chen, J.C. and Hu, C. (1999) Direct Sampling Methodology for Statistical Analysis of Scaled CMOS Technologies. IEEE Transactions on Semiconductor Manufacturing, 12, 403-408.
http://dx.doi.org/10.1109/66.806117 - 18. Chen, J., Hu, C., Wan, D., Bendix, P. and Kapoor, A. (1996) E-T Based Statistical Modeling and Compact Statistical Circuit Simulation Methodologies. IEEE International Electron Devices Meeting Technical Digest, San Francisco, 8-11 December 1996, 635-638.
http://dx.doi.org/10.1109/iedm.1996.554063 - 19. Stolk, P., Widdershoven, F. and Klaassen, D. (1998) Modeling Statistical Dopant Fluctuations in MOS Transistors. IEEE Transactions on Electron Devices, 45, 1960-1971.
http://dx.doi.org/10.1109/16.711362 - 20. Mizuno, T., Okamura, J.-I. and Toriumi, A. (1994) Experimental Study of Threshold Voltage Fluctuation Due to Statistical Variation of Channel Dopant Number in MOSFET’s. IEEE Transactions on Electron Devices, 41, 2216-2221.
http://dx.doi.org/10.1109/16.333844 - 21. Pelgrom, M.J.M., Duinmaijer, A.C.J. and Welbers, A.P.G. (1989) Matching Properties of MOS Transistors. IEEE Journal of Solid-State Circuits, 24, 1433-1439.
http://dx.doi.org/10.1109/JSSC.1989.572629 - 22. Pelgrom, M., Tuinhout, H. and Vertregt, M. (2010) Modeling of MOS Matching. In: Gildenblat, G., Ed., Compact Modeling: Principles, Techniques and Applications, Springer-Verlag, New York, 453-490.
http://dx.doi.org/10.1007/978-90-481-8614-3_15 - 23. Tian, Y. and Chan, P.K. (2010) Design of High-Performance Analog Circuits Using Wideband gm-Enhanced MOS Composite Transistors. IEICE Transaction on Electronics, E93-C, 1199-1208.
http://dx.doi.org/10.1587/transele.E93.C.1199 - 24. Carrillo, J.M., Torelli, G. and Duque-Carrillo, J.F. (2011) Transconductance Enhancement in Bulk-Driven Input Stages and Its Applications. Analog Integrated Circuits and Signal Processing, 68, 207-217.
http://dx.doi.org/10.1007/s10470-011-9603-z - 25. Mirzaie, H.K. and Hossein, S. (2011) A 0.5 V Bulk-Input OTA with Improved Common-Mode Feedback for Low- Frequency Filtering Applications. Analog Integrated Circuits and Signal Processing, 59, 83-89.
- 26. Lo, T.-Y. and Hung, C.-C. (2008) A 40-MHz Double Differen-Tial-Pair CMOS OTA with 60-dB IM3. IEEE Transactions on Circuits and Systems I: Regular Papers, 55, 258-265.
http://dx.doi.org/10.1109/TCSI.2007.910747 - 27. Hassan K. and Hossein, S. (2012) On the Design of a Low-Voltage Two Stage OTA Using Bulk-Driven and Positive Feedback Techniques. International Journal of Electronics, 99, 1309-1315.
http://dx.doi.org/10.1080/00207217.2012.669710

















