 Journal of Modern Physics, 2013, 4, 151-156 http://dx.doi.org/10.4236/jmp.2013.44A014 Published Online April 2013 (http://www.scirp.org/journal/jmp) Discussion for the Solutions of Dyson-Schwinger Equations at m ≠ 0 in QED3 Huixia Zhu1,2, Hongtao Feng3,4, Weimin Sun1,4,5, Hongshi Zong1,4 1Department of Physics, Nanjing University, Nanjing, China 2The College of Physics and Electronic Information, Anhui Normal University, Wuhu, China 3Department of Physics, Southeast University, Nanjing, China 4State Key Laboratory of Theoretical Physics, Institute of Theoretical Physics, CAS, Beijing, China 5Joint Center for Particle, Nuclear Physics and Cosmology, Nanjing, China Email: zonghs@chenwang.nju.edu.cn Received February 10, 2013; revised March 14, 2013; accepted March 25, 2013 Copyright © 2013 Huixia Zhu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT In the case of nonzero fermion mass, within a range of Ansätze for the full fermion-boson vertex, we show that Dyson-Schwinger equation for the fermion propagator in QED3 has two qualitatively distinct dynamical chiral symme- try breaking solutions. As the fermion mass increases and reaches to a critical value mc, one solution disappears, and the dependence of mc on the number of fermion flavors is also given. Keywords: QED3; Fermion Propagator; Solutions of DSEs 1. Introduction Nowadays, it is widely accepted that Quantum Chro- modynamics (QCD) in 3 + 1 dimensions is the funda- mental theory for strong interaction. Dynamical chiral symmetry breaking (DCSB) is of fundamental impor- tance for strong interaction physics. DCSB can be ex- plored via the gap equation, viz., the Dyson-Schwinger equation (DSE) for the dressed-fermion self-energy. As is well known, the gap equation has two solutions in the chiral limit, i.e. the Nambu-Goldstone (NG) solution which is characterized by DCSB, and the Wigner (WN) solution in which chiral symmetry is not dynamically broken. However, when the current quark mass m is nonzero, the quark gap equation has only one solution which corresponds to the NG phase and the solution cor- responding to the WN phase does not exist [1,2]. This conclusion is hard to understand and one will naturally ask why the Wigner solution of the quark gap equation only exists in the chiral limit and does not exist at finite current quark mass. The authors of Ref. [3] first discussed this problem and asked whether the quark gap equation has a Wigner solution in the case of nonzero current quark mass. Subsequently, the authors of Refs. [4-7] fur- ther investigated the problem of possible multi-solutions of the quark gap equation. As far as we know, partly due to the complexity of the non-Abelian character of QCD, this problem has not been solved satisfactorily in the lit- erature. In the present paper we try to propose a new ap- proach to investigate this problem in the framework of a relatively simple Abelian toy model of QCD, namely, quantum electrodynamics in 2 + 1 dimensions (QED3). As a field-theoretical model, QED3 has been exten- sively studied in recent years. It has many features simi- lar to QCD in 3 + 1 dimensions. This is because QED3 is known to have a phase where the chiral symmetry of the theory is spontaneously broken and the fermions are con- fined in this phase [8]. Moreover, QED3 is supernor- malizable, so it is not plagued with the ultraviolet diver- gences which are present in QED4. These are the basic reasons why QED3 is regarded as an interesting toy model: studying QED3 it might be possible to investigate confinement [8-10] and dynamical chiral symmetry breaking (DCSB) [11-16] within a theory which is struc- turally much simpler than QCD while sharing the same basic nonperturbative phenomena. Herein we try to use the DSEs for the fermion and photon propagators in QED3 to describe novel aspects of the interplay between explicit and dynamical chiral symmetry breaking. 2. Dyson-Schwinger Equation for Fermion Propagator The Lagrangian of QED3 with N flavors of fermions in a C opyright © 2013 SciRes. JMP  H. X. ZHU ET AL. 152 general covariant gauge in Euclidean space, ignoring the issues discuss in Ref. [15], can be written as ifications that anticipate your paper as one part of the entire jour- nals, and not as an independent document. Please do not revise any of the current designations. 2 11 A 42 F 1, ,jN 22 Ap Bp 1,Smp 1,Smp 2 1 N jj j LieAm (1) where the 4 × 1 spinor j is the fermion field with being the flavor indices. Based on Lorentz structure analysis, the inverse fer- mion propagator in the chiral limit can be written as 1 Spip (2) One assumes that dressed fermion propagator at finite m is analytic in the neighborhood of m = 0, so the can be written as 1 11 0 22 22 , , mSmp Smp S pm ipApBp ipCmp ipEp Fp 2 2 d ,, m Dmp 2 2 ,, ,. Cmp Dmp (3) where 22 22 Ep Ap Fp Bp Setting e2 = 1, the DSE for the fermion propagator can be written as 11 0 3 3 ,, d,;, 2π Smp Smp kSmkmpkD ,mpk 1 0,Smp ;,mpk (4) where is the bare inverse fermion propagator and is the full fermion-photon vertex. Sub- stituting Equation (3) into Equation (4), one can obtain 3 2 23 1d 142π Tr,; , k Ep p ipSmkm ,pkDmq (5) and 3 2 3 1d 42π Tr,; , k Fp m Smk mp ,kD mq (6) where q = p – k. The full photon propagator can be writ- ten as 2 4 22 q qq q q ,1, qq Dmq qm 2 ,mq (7) with the vacuum polarization defined by 22 2 ,,mqq qqmq (8) The DSE satisfied by the photon vacuum polarization tensor reads 3 2 3 d ,2π Tr,; ,, k mq N Smp mpkSmk 2 ,mq (9) The boson polarization has an ultraviolet divergence which is present only in the longitudinal part. By applying the projection operator 2 3qq Pq (10) one can remove this divergence and obtain a finite vac- 2 ,mq [15]. uum polarization The DSEs for the photon and fermion propagators form a set of coupled integral equations for the three 22 2 ,and, Ep Fpmq ;,mpk once scalar functions the full fermion-photon-vertex is known. Unfortunately, although several works attempts to re- solve the problem, none of them are completely satisfac- tory [17-23]. Thus, in phenomenological applications, one often proceed by adopting reasonable approximation for ;,mpk such that Equations (5), (6) and (9) are reduced to a closed system of equations which may be solved directly. In this letter, following Ref. [15], we choose the following AnsÄatzefor the full fermion-pho- ton vertex 22 ;, ,mpkfE pEk (11) and the form of function f is: 1) 1; 2) 22 1 2Ep Ek 22 Ep Ek. ; 3) The first one is the bare vertex. This structure plays the most dominant role in the full fermion-photon vertex in high energy region and the full fermion-photon vertex reduces to it in large momentum limit. The second form is inspired by the BC-vertex [18]. Previous works [15,24] show that the numerical results of DSEs employing this Ansatz is as good as that employing BC and CP vertex [19]. Since the numerical results obtained using the last Ansatze coincide very well with earlier investigation [15,25], we choose this one as a reasonable Ansatze to be used in this work. Using those AnsÄatzefor the full fer- mion-photon vertex, the coupled DSEs for the fermion propagator and photon vacuum polarization reduce to the following form Copyright © 2013 SciRes. JMP  H. X. ZHU ET AL. Copyright © 2013 SciRes. JMP 153 22 2 1 f q q 3 2 23 2222 22 2d 1(2π) Ekpq kq k Ep pqEkk Fk (12) 2 3 2 32 22222 d 22π Fk f k Fp m qEkk Fk 2 1q (13) 22 22 222 3 2 23 222 22222 23 4d 2π kE pkkq Nk qqEkkFkE p kqq f pF p 22 Ep Ap 22 (14) where the Landau gauge has been chosen. In the chira limit, and pBp 2 2 Bp 2 2 Bp 20Bp . From Equations (12)-(14), it is not difficult to find that the above coupled equations have one Wigner solution and two dynamical symmetry breaking solu- 20Bp Bp tions: and . As was point- 2 0Bp ed out in Ref. [4], if is a solution of the gap equation in the chiral limit, then so is . While these two solutions are distinct, the chiral symmetry en- tails that each yields the same pressure. In the chiral limit, the two dynamical symmetry breaking solutions are symmetric about the Wigner solution Bp . However, just as will be shown below, this might be changed when the fermion mass is not zero. 3. Numerical Results Our next task is to solve for the two scalar functions and 2 ,Emp 2 , mp . These two functions can be obtained by numerically solving the three coupled inte- gral Equations (12)-(14). Starting from E = 1, F = 1 and П = 1, we iterate the three coupled integral equations until all the three functions converge to a stable solution which is plotted in Figure 1 (solid line). From Figure 1, it is easy to find that all the three sca- lar functions in the DCSB phase (N = 1) are constant in the infrared region, while in the ultraviolet region the vector function behaves as 21Ap and the photon vacuum polarization behaves as 21qq . Never- theless, in contrast to the case of massless QED3 [15], in the large momentum region, the fermion self-energy re- duces to the bare mass m in Equation (6). Since all the three functions are positive in the whole range of p2, we define them as the “+” solution. If we do interation starting from F = −1, E = 1 and П = 1, we can obtain another stable solution. The typical be- haviors of the three functions in the DCSB phase for a fixed mass and number of fermion flavors are also plot- ted in Figure 1 (the dotted line). From Figure 1, we see that the DSEs for the fermion propagator has two distinct nonzero solutions. Especially, the infrared value of the fermion self-energy is negative, so we define it as the “−” solution. In the low energy region, each of the three functions in the second solution is also almost constant, but it is different from the corresponding one in the “+” solution. As p2 or q2 increases, each function of the “−” solution approach to the corresponding one of the “+” solution. To reveal the difference between these two solutions, we consider m as a continuous parameter in the DSEs. We plot the infrared value of E, F, П in Figure 2. When m = 0, from DSEs one obtains one E and П, but two F which are symmetric about F = 0 in Figure 2 for each vertex ansatze. For the “+” solution of DSEs, as m in- creases, E(0) and F(0) increases while П(0) decreases. However, the three infrared values in the “−” solution show a different trend as m increases. When m reaches its critical value, we obtain only one solution for DSEs. In addition, from Figure 2, it can be seen that the critical mass exists for any truncated scheme of DSEs used in this work. Furthermore, we investigate the influence of the num- ber of fermion flavors on the critical mass. By employing ansatze 2, we can obtain the relation between the critical mass and the number of fermion flavors and it is plotted in Figure 3. We observe that the critical mass decreases as N increases and it vanishes at N = Nc, which is similar to the critical number of fermion flavors for DCSB in the chiral limit [16]. 4. Conclusion To summarize, in this paper, working in the framework of Dyson-Schwinger equations and employing a range of ansatze for the full fermion-photon vertex of QED3, westudy the interplay between explicit and dynamical chiral symmetry breaking in QED3. In the case of non- zero fermion mass, it is found that, besides the ordinary solution, the fermions gap equation has another solution which has not been reported in the previous work of QED3. In the low energy region, one observes that these two solutions are apparently different, but in the high energy region they coincide with each other. In addition, it is found that this solution exists only when the mass is 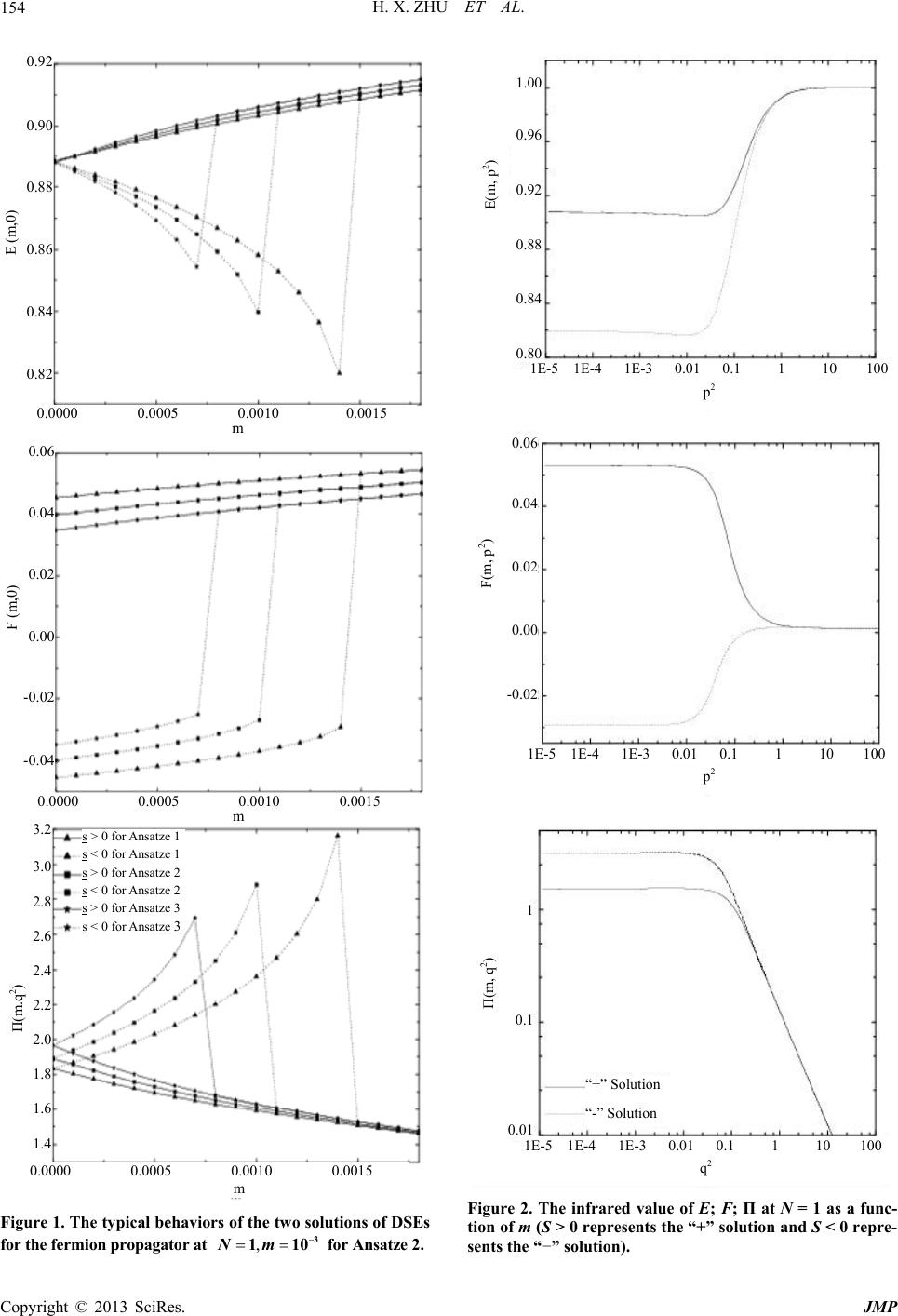 H. X. ZHU ET AL. 154 0.92 0.90 0.88 0.86 0.84 0.82 0.0000 0.0005 0.0010 1.00 0.96 0.92 0.88 0.84 0.80 0.0015 m 0.0000 0.0005 0.0010 0.0015 m 0.06 0.04 0.02 0.00 -0.02 -0.04 F (m,0) 0.0000 0.0005 0.0010 0.0015 m 3.2 3.0 2.8 2.6 2.4 2.2 2.0 1.8 1.6 1.4 Π(m.q 2 ) E (m,0) s > 0 for Ansatze 1 s < 0 for Ansatze 1 s > 0 for Ansatze 2 s < 0 for Ansatze 2 s > 0 for Ansatze 3 s < 0 for Ansatze 3 E(m, p 2 ) 1E-5 1E-4 1E-3 0.01 0.1 1 10 100 p 2 0.06 0.04 0.02 0.00 -0.02 F(m, p 2 ) 1E-5 1E-4 1E-3 0.01 0.1 1 10 100 p 2 Figure 1. The typical behaviors of the two solutions of DSEs for the fermion propagator at 3 for Ansatze 2. , Nm110 1E-5 1E-4 1E-3 0.01 0.1 1 10 100 1 0.1 0.01 Π(m, q 2 ) “+” Solution “-” Solution q 2 Figure 2. The infrared value of E; F; П at N = 1 as a func- tion of m (S > 0 represents the “+” solution and S < 0 repre- sents the “−” solution). Copyright © 2013 SciRes. JMP  H. X. ZHU ET AL. 155 0.01 1E-3 1E-4 1E-5 1E-6 N c m 0.0 0.5 1.0 1.5 2.0 2.5 N Figure 3. The relation between the critical mass and the number of fermion flavors. smaller than a critical value. The critical mass decreases apparently with the rise of the number of fermion flavors and vanishes at a critical value Nc, which corresponds to the critical number of fermion flavors of QED3 in the chiral limit. It is an interesting phenomena which deserve further investigations. 5. Acknowledgements This work was supported by the National Natural Sci- ence Foundation of China (Grant No. 11047005, 11105029, 10935001, and 11075075) and the Research Fund for the Doctoral Program of Higher Education (un- der Grant No 2012009111002). REFERENCES [1] C. D. Roberts and A. G. Williams, “Dynamical Chiral- Symmetry Breaking and Confinement with an Infra- red-Vanishing Gluon Propagator,” Physical Review D, Vol. 49, No. 9, 1994, pp. 4683-4693. doi:10.1103/PhysRevD.49.4683 [2] C. D. Roberts and S. M. Schmidt, “Dyson-Schwinger Equations: Density, Temperature and Continuum Strong QCD,” Progress in Particle and Nuclear Physics, Vol. 45, Suppl. 1, 2000, pp. S1-S103. doi:10.1016/S0146-6410(00)90011-5 [3] H. S. Zong, W. M. Sun, J. L. Ping, X. F. Lu and F. Wang, “Does There Exist Only One Solution of the Dyson- Schwinger Equation for the Quark Propagator in the Case of Non-Zero Current Quark Mass,” Chinese Physics Let- ters, Vol. 22, No. 12, 2005, pp. 3036-3039. doi:10.1088/0256-307X/22/12/014 [4] L. Chang, Y. X. Liu, M. S. Bhagwat, C. D. Roberts and S. V. Wright, “Dynamical Chiral Symmetry Breaking and a Critical Mass,” Physical Review C, Vol. 75, No. 1, 2007, Article ID: 015201. doi:10.1103/PhysRevC.75.015201 [5] R. Williams, C. S. Fischer and M. R. Pennington, “qq Barq Condensate for Light Quarks Beyond the Chiral Limit,” Physics Letters B, Vol. 645, No. 2-3, 2007, pp. 167-172. doi:10.1016/j.physletb.2006.12.055 [6] R. Williams, C. S. Fischer and M. R. Pennington, “Quark Condensates: Flavour Dependence,” Acta Physica Polo- nica B, Vol. 38, No. 9, 2007, pp. 2803-2810. [7] Y. Jiang, H. Gong, W. M. Sun and H. S. Zong, “Wigner Solution of the Quark Gap Equation at Nonzero Current Quark Mass and Partial Restoration of Chiral Symmetry at Finite Chemical Potential,” Physical Review D, Vol. 85, No. 3, 2012, Article ID: 034031. doi:10.1103/PhysRevD.85.034031 [8] P. Maris, “Confinement and Complex Singularities in 3-Dimensional QED,” Physical Review D, Vol. 52, No. 10, 1995, pp. 6087-6097. doi:10.1103/PhysRevD.52.6087 [9] C. J. Burden, J. Praschifka and C. D. Roberts, “Photon Polarization Tensor and Gauge Dependence in 3-Dimen- sional Quantum Electrodynamics,” Physical Review D, Vol. 46, No. 6, 1992, pp. 2695-2702. doi:10.1103/PhysRevD.46.2695 [10] G. Grignani, G. Semenoff and P. Sodano, “Confinement- Deconfinement Transition in Three-Dimensional QED,” Physical Review D, Vol. 53, No. 12, 1996, pp. 7157-7161. doi:10.1103/PhysRevD.53.7157 [11] J. M. Cornwall, “Confinement and Chiral-Symmetry Breakdown Estimates of FΠ and of Effective Quark masses,” Physical Review D, Vol. 22, No. 6, 1980, pp. 1452-1468. doi:10.1103/PhysRevD.22.1452 [12] R. D. Pisarski, “Chiral Symmetry Breaking in 3-Dimen- sional Electrodynamics,” Physical Review D, Vol. 29, No. 10, 1984, pp. 2423-2426. doi:10.1103/PhysRevD.29.2423 [13] T. Appelquist, et al., “Critical Behavior in (2 + 1)-Di- mensional QED,” Physical Review Letters, Vol. 60, No. 25, 1988, pp. 2575-2578. doi:10.1103/PhysRevLett.60.2575 [14] D. Nash, “Higher-Order Corrections in (2 + 1)-Dimen- sional QED,” Physical Review Letters, Vol. 62, No. 26, 1989, pp. 3024-3026. doi:10.1103/PhysRevLett.62.3024 [15] P. Maris, “Influence of the Full Vertex and Vacuum Po- larization on the Fermion Propagator in (2 + 1)-Dimen- sional QED,” Physical Review D, Vol. 54, No. 6, 1996, 4049-4058. doi:10.1103/PhysRevD.54.4049 [16] H. T. Feng, W. M. Sun, F. Hu and H. S. Zong, “The In- fluence of the Gauge Boson Mass on the Critical Number of the Fermion Flavors in QED3,” International Journal of Modern Physics A, Vol. 20, No. 13, 2005, pp. 2753- 2762. doi:10.1142/S0217751X05021130 [17] A. Bashir, A. Huet and A. Rays, “Gauge Dependence of Mass and Condensate in Chirally Asymmetric Phase of Quenched Three-Dimensional QED,” Physical Review D, Vol. 66, No. 2, 2002, Article ID: 025029. doi:10.1103/PhysRevD.66.025029 [18] J. S. Ball and T. W. Chiu, “Analytic Properties of the Vertex Function in Gauge-Theories,” Physical Review D, Vol. 22, No. 10, 1980, pp. 2542-2549. doi:10.1103/PhysRevD.22.2542 Copyright © 2013 SciRes. JMP  H. X. ZHU ET AL. Copyright © 2013 SciRes. JMP 156 [19] D. C. Curtis and M. R. Pennington, “Truncating the Schwinger-Dyson Equations-How Multiplicative Renor- malizability and the Ward Identity Restrict the 3-Point Vertex in QED,” Physical Review D, Vol. 42, No. 12, 1990, pp. 4165-4169. doi:10.1103/PhysRevD.42.4165 [6] J. E. King, “Transverse Vertex and Gauge Technique in Quantum Electrodynamics,” Physical Review D, Vol. 27, No. 7, 1983, pp. 1821-1829. [7] A. KizilersÄu, M. Reedders and M. R. Pennington, “One-Loop QED Vertex in Any Covariant Gauge: Its Complete Analytic Form,” Physical Review D, Vol. 52, No. 2, 1995, pp. 1242-1259. doi:10.1103/PhysRevD.52.1242 [8] C. J. Burden and P. C. Tjiang, “Deconstructing the Vertex Ansatz in Three-Dimensional Quantum Electrodynam- ics,” Physical Review D, Vol. 58, No. 8, 1998, Article ID: 085019. [9] K.-I. Kondo and H. Nakatani, “Cutoff Dependence of Self-Consistent Solutions in Unquenched QED3,” Pro- gress Theoretical Physics, Vol. 87, No. 1, 1992, pp. 193- 206. doi:10.1143/PTP.87.193 [10] C. S. Fischer, R. Alkofer, T. Dahm and P. Maris, “Dy- namical Chiral Symmetry Breaking in Unquenched QED3,” Physical Review D, Vol. 70, No. 7, 2004, Article ID: 073007. doi:10.1103/PhysRevD.70.073007 [11] T. Appelquist, M. Bowick, D. Karabali and L. C. R. Wi- jewardhana, “Spontaneous Chiral-Symmetry Breaking in 3-Dimensional QED,” Physical Review D, Vol. 33, No. 12, 1986, pp. 3704-3713. doi:10.1103/PhysRevD.33.3704
|