Journal of Modern Physics, 2013, 4, 49-56
http://dx.doi.org/10.4236/jmp.2013.44A008 Published Online April 2013 (http://www.scirp.org/journal/jmp)
Quasi-Biennial Modulation of the Solar Neutrino Flux:
A “Telescope” for the Solar Interior
Loris D’Alessi1, Antonio Vecchio1, Vincenzo Carbone1,2*, Monica Laurenza3, Marisa Storini3
1Dipartimento di Fisica, Università della Calabria, Cosenza, Italy
2Liquid Crystal Laboratory (INFM), Cosenza, Italy
3INAF/IAPS-Roma, Via del Fosso del Cavaliere, Roma, Italy
Received February 18, 2013; revised March 21, 2013; accepted March 31, 2013
Copyright © 2013 Loris D’Alessi et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
An oscillating magnetic field deep within the solar radiative region can significantly alter the helioseismic g-modes. The
presence of density gradients along g-modes, can excite Alfvén waves resonantly, the resulting waveforms show sharp
spikes in the density profile at radii comparable with the neutrino’s resonant oscillation length. This process should ex-
plain the observed quasi-biennial modulation of the solar neutrino flux. If confirmed, the coupling between solar neu-
trino flux and g-modes should be used as a “telescope” for the solar interior.
Keywords: Solar Neutrinos; Solar Cycle; Solar Interior
1. Introduction Sakurai claimed that fluctuations of the core temperature,
which is responsible of the pp chain efficiency, should be
at the origin of this quasi-biennial modulation [6]. How-
ever the analysis by Lanzerotti [7] carried on a set of data
which cover a longer time period, exclude any connection
between events in the core with the ones which occur in
the photosphere. The results of analysis of Kamiokande
data over the cycle 22 of the 11-yr solar cycle [8] showed
that there is no correlation of the solar neutrino flux with
sunspot numbers on 11-yr time scale.
Time variability of solar neutrino flux has been studied
since the appearance of the first results of Homestake
experiment [1]. In an early attempt to interpret the dis-
crepancy between theoretical and observed flux, Sheldon
[2] suggested a dependence of neutrino flux with solar
activity, due to a time variable production rate of the
neutrinos in the core of the Sun. The most famous evi-
dence of the solar cycle is the time variation of sunspots
number, with a characteristic period of about 11 years,
extensively investigated in the past (see e.g., Ref. [3]).
The occurrence of the solar cycle is related to the dynamo
effect that generates the magnetic field of the Sun through
the α-ω process (the usual α-effect coupled with the dif-
ferential rotation) [4]. The spatial behaviour of the solar
cycle is related to the latitudinal migration of magnetic
structures toward the solar equator as the 11-year cycle
goes on, thus generating the characteristic “butterfly dia-
gram” in both space and time domain. Superimposed on
these large-scale effects, the presence of small-scale ap-
parently stochastic fluctuations is observed [5].
Apart from the 11-year cycle, intra-cycle periodicities
have been discovered in many solar activity proxies. The
most prominently recognized periods are in the so called
quasi-biennial oscillations (QBOs) range on time scales
from 1.5 to 3.5 years [9-12]. This periodicity is better
detected in correspondence of main cycle maxima and it
suffers, as the 11-year cycle, of period length modulation
[13]. Quite interestingly, corresponding QBOs have been
found also in other contexts related to solar variability, as
in solar wind fluctuations, interplanetary magnetic field
intensity, galactic cosmic ray (CR) flux [14-17] energetic
proton fluxes recorded in the interplanetary space [18] and
in the solar rotation rate [19]. In they early work, Sakurai
[6] invoked the presence of the quasi-biennial modula-
tion for solar neutrino flux, in an attempt to solve the
puzzle of missing neutrinos [20]. To date the puzzle has
been solved in favour of neutrino flavour transformation
However, through the analysis of Homestake data Sa-
kurai [6] showed the existence of a quasi-biennial perio-
dicity both in the solar neutrino flux and in the sunspot
number. In order to make a connection between the pe-
riodicity observed both in solar neutrino and sunspot data,
*Corresponding author.
C
opyright © 2013 SciRes. JMP

L. D’ALESSI ET AL. 50
[21], also implying a rest mass for neutrinos. Neverthe-
less, the origin of the biennial modulation of the solar
neutrino flux and its interaction with the solar magnetic
field are still debated [12,22-27].
These modulations should be induced by direct cou-
pling of neutrino flux with solar magnetic field through
neutrino magnetic moment. However, based on Kam-
LAND data analysis constraint [28], assuming an upper
bound for neutrino magnetic moment
12
10
B



2
2.810 
 
1
0
m
jm
j
(1)


a neutrino oscillation length λosc ≈ 100 - 200 km and
magnetic field fluctuation with amplitude δB ≈ 50 - 100
kG, the deviation from the mean rate for SFP mechanism
results to be of the order of % [28]. This means
that the coupling of neutrino’s magnetic moment and
magnetic field gives negligible effects. On these basis,
the most reliable mechanism seems to be the modulation
of the production rate of the nuclear reactions or the
variation of physical parameters, mainly the density, at the
solar core. In order to affect appreciably the neutrino flux,
the density fluctuations have to satisfy both the following
requests at the position of the MSW oscillation [29,30]:
1) The correlation length of these fluctuations has to be
of the same order of neutrino oscillation length;
2) The fluctuations amplitude have to be at least of ~1%.
The most plausible mechanism, which in principle
could originate fluctuations in matter density with the
required properties, is the Alfvén/g-modes resonance [31].
The presence of density gradients along g-modes, can
excite Alfvén waves resonantly, the resulting waveforms
show sharp spikes in the density profile at radii compa-
rable with the neutrino’s resonant oscillation length.
Hence, the study of short-term periodicities of the solar
cycle should lead to improve knowledge of the global
properties of the Sun, with particular regard to solar neu-
trinos and energetic particle emission. In particular, the
possible coupling neutrino-solar activity can help to un-
derstand the physical processes occurring in the solar
deeper layers not accessible to helioseismic probing.
In the present paper we resume the study of the quasi-
biennial solar cycle (see [12,32-33]) by investigating the
time evolution of two different datasets, through the em-
pirical mode decomposition (EMD), with particular at-
tention to the statistical significance of the analysis. We
claim that the modulation can be the manifestation of the
interaction of solar neutrino flux with Alfvén/g-mode
resonance modulated by an oscillating magnetic field
deep within the solar radiative region.
2. The Neutrino Datasets
In order to investigate the relationship between solar
neutrinos and magnetic activity, we report the results of
EMD analysis carried out solar neutrino flux data re-
corded from the Homestake experiment (dataset νH) (a
total of 108 records from 1970 to 1994 [34]) and from the
SAGE experiment (dataset νS) (a total of 168 records from
1990 to 2008 [35]). The data from these two experiments
cover a time window of ~20 yr, passing through the
maxima of two solar cycles (Cycles 21 and 22 for Home-
stake data and Cycles 22 and 23 for SAGE data). The
EMD results for the two solar neutrino datasets have been
compared with that obtained from the data of several solar
cycle indicators: sunspot number (SN) and area (SA), flux
of interplanetary protons in the energy range 0.50 - 0.96
MeV/nucleon measured by the charged particles meas-
urements experiment (channel P2) aboard the IMP8
spacecraft (P2) and cosmic ray intensity measured by the
Rome neutron monitor with cutoff rigidity of 6 GV
(NM)1.
3. The Empirical Mode Decomposition
The periodicities and their relative amplitudes have been
identified through the EMD, a technique developed to
process nonstationary data [36] and successfully applied
in different contexts, e.g. [37,38]. In the EMD framework,
a time series X(t) is decomposed into a finite number of
oscillating intrinsic mode functions (IMF) as
tCtrt




X
(2)
The IMFs Cj(t) represent a set of basis functions ob-
tained from the dataset under analysis by following the
“sifting” procedure described by Huang et al. [36]. This
procedure starts by identifying local minima and local
maxima of the raw signal X(t). The envelopes of maxima
and minima are then obtained through cubic splines and
the mean between them, namely m1(t), is calculated. The
differences between the raw time series and the mean
series






htXt mt
11
, represents an IMF only if it
satisfies two criteria: 1) the number of extremes and zero
crossings does not differ by more than one; 2) at any point,
the mean value of the envelopes defined by the local
maxima and the local minima is zero.
4. Results and Discussion
The EMD represents a powerful tool to study the solar
QBOs and highly nonstationary signal. Since these oscil-
lations are high during the activity maxima [9,11,13] and
their frequency is not constant from a cycle to another
[13] the EMD is more suitable than the classical Fourier
and wavelet analysis, to properly identify the QBOs. In
fact it is well known that, in presence of nonstationary
1SN and SA data at: http://solarscience.msfc.nasa.gov/SunspotCycle.
shtml; P2 data at: http://sdwww.jhuapl.edu/IMP/imp_cpme_data.html;
CR data at: http://www.fis.uniroma3.it/svirco/.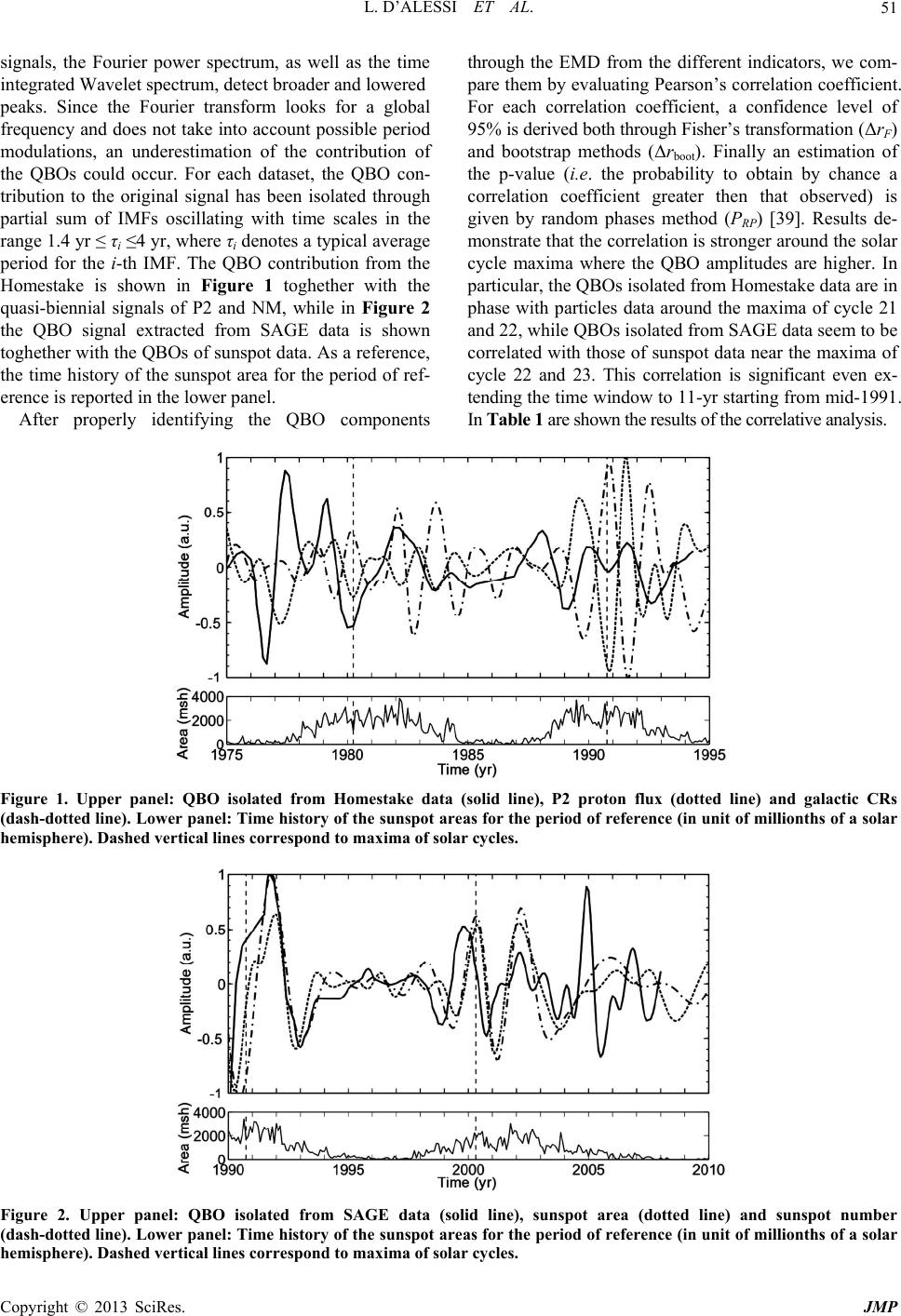

L. D’ALESSI ET AL.
CopyrigJMP
51
signals, the Fourier power spectrum, as well as the time
integrated Wavelet spectrum, detect broader and lowered
peaks. Since the Fourier transform looks for a global
frequency and does not take into account possible period
modulations, an underestimation of the contribution of
the QBOs could occur. For each dataset, the QBO con-
tribution to the original signal has been isolated through
partial sum of IMFs oscillating with time scales in the
range 1.4 yr ≤ τi ≤4 yr, where τi denotes a typical average
period for the i-th IMF. The QBO contribution from the
Homestake is shown in Figure 1 toghether with the
quasi-biennial signals of P2 and NM, while in Figure 2
the QBO signal extracted from SAGE data is shown
toghether with the QBOs of sunspot data. As a reference,
the time history of the sunspot area for the period of ref-
erence is reported in the lower panel.
After properly identifying the QBO components
through the EMD from the different indicators, we com-
pare them by evaluating Pearson’s correlation coefficient.
For each correlation coefficient, a confidence level of
95% is derived both through Fisher’s transformation (ΔrF)
and bootstrap methods (Δrboot). Finally an estimation of
the p-value (i.e. the probability to obtain by chance a
correlation coefficient greater then that observed) is
given by random phases method (PRP) [39]. Results de-
monstrate that the correlation is stronger around the solar
cycle maxima where the QBO amplitudes are higher. In
particular, the QBOs isolated from Homestake data are in
phase with particles data around the maxima of cycle 21
and 22, while QBOs isolated from SAGE data seem to be
correlated with those of sunspot data near the maxima of
cycle 22 and 23. This correlation is significant even ex-
tending the time window to 11-yr starting from mid-1991.
In Table 1 are shown the results of the correlative analysis.
Figure 1. Upper panel: QBO isolated from Homestake data (solid line), P2 proton flux (dotted line) and galactic CRs
(dash-dotted line). Lower panel: Time history of the sunspot areas for the period of reference (in unit of millionths of a solar
hemisphere). Dashed vertical lines correspond to maxima of solar cycles.
Figure 2. Upper panel: QBO isolated from SAGE data (solid line), sunspot area (dotted line) and sunspot number
(dash-dotted line). Lower panel: Time history of the sunspot areas for the period of reference (in unit of millionths of a solar
hemisphere). Dashed vertical lines correspond to maxima of solar cycles.
ht © 2013 SciRes.

L. D’ALESSI ET AL. 52
Notes on tables contents. In Tables 1-3 are reported,
for different couples of QBOs extracted from datasets X
and Y, the corresponding Pearson correlation coefficient
r evaluated in the period indicated in the caption. ΔrF and
Δrboot represent the 95% confidence intervals for the cor-
relation coefficient from Fisher’s and bootstrap tests,
respectively. PRP indicates the probability, calculated
through the random phases test, to obtain values greater
than rXY due to chance.
namely the continuity equation for mass density
5. The Magneto-Gravity Modes
The observed correlation between solar quasi-biennial
cycle and solar neutrino flux fluctuations on quasi-bien-
nial time scales could represent a direct observation of
instabilities induced by quasi-biennial dynamo effects in
the deeper regions of solar radiative zone. The theory of
coupling between large scale magnetic fields and solar
matter has been investigated by Burgess et al. [31]. In
particular, in the presence of backgroud magnetic fields of
reasonable intensity, density gradients allows g-modes to
excite Alfvén waves resonantly, causing mode energy to
be funnelled along magnetic field lines away from the
solar equatorial plane.
Magneto-gravity waves are described by the usual
compressible, ideal magnetohydrodynamic equations,
Table 1. Results of correlative analysis for Homestake, en-
ergetic proton and cosmic ray data for 5 yr around maxima
of cycle 21 (1980.25).
X-Y r ΔrF Δrboot PRP
νH-P2 0.96 [0.90, 0.98] [0.91, 0.98] 0.01
νH-NM –0.90 [–0.96, –0.75] [–0.95, –0.78] 0.06
P2-NM –0.98 [–0.99, –0.95] [–0.99, –0.97] 0.01
Table 2. Results of correlative analysis for Homestake, en-
ergetic proton and cosmic ray data for 5 yr around maxima
of cycle 22 (1990.75).
X-Y r ΔrF Δrboot PRP
νH-P2 –0.92 [0.82, 0.97] [0.82, 0.97] 0.03
νH-NM 0.93 [–0.99, –0.97] [–0.99, –0.98] 0.01
P2-NM –0.99 [–0.97, –0.80] [–0.96, –0.85] 0.03
Table 3. Results of correlative analysis for SAGE, sunspot
number and area for 11 yr starting from mid-1990.
X-Y r ΔrF Δrboot PRP
νS-SA 0.58 [0.46, 0.69] [0.45, 0.69] <0.01
νS-SN 0.67 [0.56, 0.75] [0.53, 0.78] <0.01
SA-SN 0.89 [0.85, 0.92] [0.86, 0.92] <0.01

0
t
 

 
v (3)
the momentum equation with the gravity term
 
1
4π
P
t



 

 


vvvg BB
(4)
and the magnetic field induction equation

t


 

BvB
(5)
The system of equations can be closed by relating the
pressure P to the mass density through an energy equa-
tion

dd 1
dd
PP Q
tt






 (6)
where d/dt is the total time derivative, γ is the ratio of heat
capacities, and Q is the sum of all energy density sources
and losses, such as heat conductivity, viscosity and ohmic
dissipation.
Assuming an equilibrium situation where the velocity
field and current density are both zero, Equations (3)-(6)
are linearized by using low-frequency approximation, in
order to filter out the pressure p-modes, and an exponent-
tial density profile. A plane geometry with a local gravity
directed along the z-axis and the background magnetic
field along the x-axis is used. Background quantities de-
pend on z, and a standard mass-density profile coming
from solar models

exp zH  


,,,exp xy
0c is assumed (here
the density at the solar centre ρc and the density
height-scale H are constant) [29]. All fluctuating quanti-
ties depends on space and time through
xyztAzikx kyt 



A
If we consider a slowly varying background magnetic
field, we expect that the system, which varies on times of
the order of the helioseismic characteristic periods, has
enough time to adapt the configuration corresponding to
the instantaneous amplitude of the background magnetic
field (adiabatic hypothesis). Under this assumption, by
using a background magnetic field which varies in time
according to


00 0
x
Bf  Be, where 0

 

, we ob-
tain two equations for the Fourier coefficients of magnetic
field fluctuations 00
Bf t 





bB and the velocity
fluctuations v



2
00
xx
x
Axzx
iik
b P
ivtikb
z



 
  

 





bv ve
g
ve
(7)
(“primed” quantities are fluctuations). The above set of
equations is formally identical to that founded by Burgess

L. D’ALESSI ET AL. 53
et al. [31], apart for the fact that in our case
 
2
22 0
0
4π
Bf t
A
vt



is a time-dependent Alfvén speed.
After some algebraic calculations we finally obtain an
equation for the fluctuating magnetic field, whose solution
determines all other fluctuating quantities
 
 
22 2
22
22
2
1d
xA
2
2
22
dd
d
10
z
z
z
N z
bb
xA
kv t
g
z
N z
kb






222
z
kv t








(8)
where the perpendicular wave-vector is
x
y
kkk

and we defined the Brunt-Väisälä frequency
 
2
Nz gz Pz
00
00
dd
11
dd
P
z






0B
 
,cosht
 (9)
which represents the characteristic frequency of the sys-
tem. Equation (8) describes magneto-gravity waves. In
the limit 0 it leads to the standard helioseismic
g-modes. In absence of gravity and B0 = cost. Equation
(8) describes Alfvén waves with frequency ω = ΩA = kx
vA. By retaining both gravitation and magnetic field a
new singular point occurs when the coefficient of the
second derivative term in Equation (8) vanishes. Since
this happens at ω = ΩA, it can be viewed as being due to
resonance between g-modes and Alfvén waves [31]. Let
us come back to the Sun. Since ΩA varies with the dis-
tance from the centre of the Sun, while, according to
usual helioseismology the g-modes frequency is inde-
pendent on position, the resonance occurs at a particular
radius inside the Sun, namely when ΩA crosses the fre-
quency of one of the g-modes. The occurrence of the
resonance depends on the value of B0. This means that, in
our case, the existence of the resonance is modulated in
time by the term f(ω0t), that is the resonance is time-de-
pendent.
Solutions of Equations (7) gives the eigenvalue spec-
trum as roots of the trascendental equation [31]
An


 
0cosht
 (10)
where
x
kC

 
where C0(t) represents the time-dependent Alfvén veloc-
ity at the solar centre, and
Accordingly, the instantaneous resonant position is
given by
 
0π
,2πln tan
4
x
kC t
Antn i
Nk H
1
π



 





 







,2lnRecosh,
r
znt Hnt   

(11)
The time dependence of solution of Equation (10) re-
sults in a modulation of the distance between neighbor-
ing resonant layers with the same period of the back-
ground magnetic field. This is shown in Figure 3, where
we report the time evolution of the distance as a function
of the position of the resonance




d,1, ,
rr r
zntznt znt

(12)
The background magnetic field is assumed to have a
sinusoidal variation, with a profile defined by
22
00
0,cos sin
22
tt
ft


 

 
 
1
π
(13)

y
where 0r  
3
10 


and the function f is defined in the
interval [ε, 1] (we used ).
As noted by Burgess et al. [31], for reasonably values
of the background magnetic field intensity, the distance
between resonant layers, at the neutrino’s resonant region,
are of the order of the neutrino’s oscillation length. In
particular the spikes which occur in density profiles, as a
consequence of the resonance, could increase the prob-
ability of interactions between neutrino flux and solar
matter [29].
In Figure 4 we report the time evolution of the lagran-
gian density perturbation
   


1
exp,1 2,1
r
C
zznt Hidnt






 

(14)
where d(n, t) denotes the growing factor of the eigenfre-
quency


11id
 , and C is defined as follows




2
122 2
1
,1
41
1
ph
s
vntkH
Cci

















 


(15)




1
where ,,
p
hx
. As it is evident, the reso-
nance oscillates in time with a frequency ω0.
vnt ntk  
6. Conclusions
Recent analysis carried on BiSON and GOLF data [40]
show that quasi-biennial signal has the same amplitude
for p-modes at all frequencies. On the other hand the
11-yr modulation affects predominantly high frequency
p-modes occuring on shallow regions close to the solar
surface. This suggests that the dynamo mechanism re-
sponsible of the mean cycle has its origin at shallow re-
gions of the solar interior (resonably located near the bot-
tom of the shear layer extending 5% below the surface),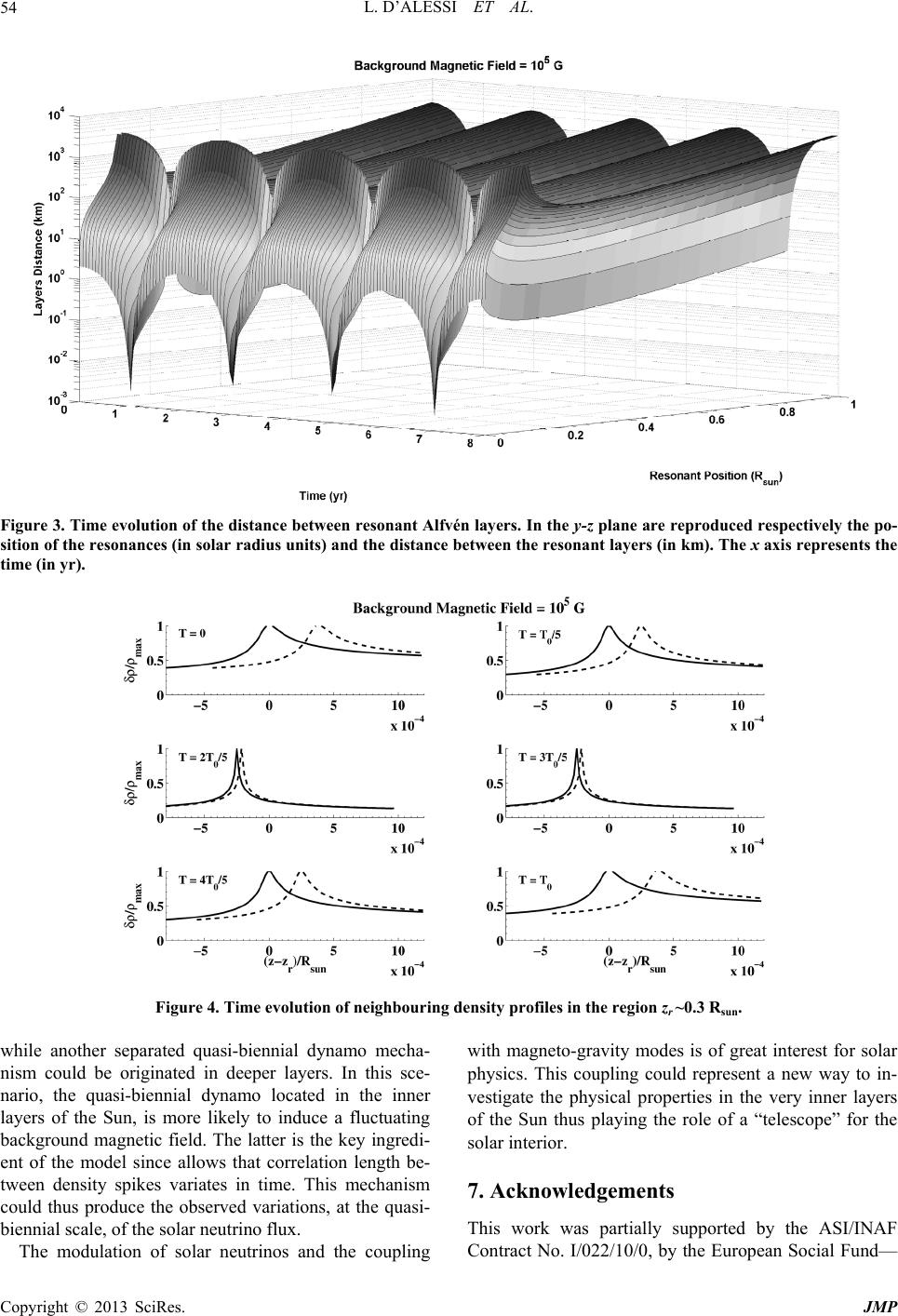

L. D’ALESSI ET AL. 54
Figure 3. Time evolution of the distance between resonant Alfvén layers. In the y-z plane are reproduced respectively the po-
sition of the resonances (in solar radius units) and the distance between the resonant layers (in km). The x axis represents the
time (in yr).
Figure 4. Time evolution of neighbouring density profiles in the region zr ~0.3 Rsun.
while another separated quasi-biennial dynamo mecha-
nism could be originated in deeper layers. In this sce-
nario, the quasi-biennial dynamo located in the inner
layers of the Sun, is more likely to induce a fluctuating
background magnetic field. The latter is the key ingredi-
ent of the model since allows that correlation length be-
tween density spikes variates in time. This mechanism
could thus produce the observed variations, at the quasi-
biennial scale, of the solar neutrino flux.
with magneto-gravity modes is of great interest for solar
physics. This coupling could represent a new way to in-
vestigate the physical properties in the very inner layers
of the Sun thus playing the role of a “telescope” for the
solar interior.
7. Acknowledgements
This work was partially supported by the ASI/INAF
Contract No. I/022/10/0, by the European Social Fund— The modulation of solar neutrinos and the coupling

L. D’ALESSI ET AL. 55
European Commission and Regione Calabria. Thanks are
due also to the Italian PNRA for the use of the RAC-
ANT database prepared at IFSI-Roma.
REFERENCES
[1] R. Davis Jr., D. S. Harmer and K. C. Hoffman, “Search
for Neutrinos from the Sun,” Physical Review Letters,
Vol. 20, No. 21, 1968, pp. 1205-1209.
doi:10.1103/PhysRevLett.20.1205
[2] W. R. Sheldon, “Possible Relation of a Null Solar Neu-
trino Flux to the II Year Solar Cycle,” Nature, Vol. 221,
No. 5181, 1969, pp. 650-651. doi:10.1038/221650b0
[3] R. A. Donahue and S. L. Baliunas, “Periodogram Analy-
sis of 240 Years of Sunspot Records,” Solar Physics, Vol.
141, No. 1, 1992, pp. 181-197. doi:10.1007/BF00155911
[4] Ya. B. Zeldovich, A. A. Ruzmaikin and D. D. Sokoloff,
“Magnetic Fields in Astrophysics,” Gordon & Breach,
New York, 1983.
[5] A. Pontieri, F. Lepreti, L. Sorriso-Valvo, A. Vecchio and
V. Carbone, “A Simple Model for the Solar Cycle,” Solar
Physics, Vol. 213, No. 1, 2003, pp. 195-201.
doi:10.1023/A:1023227503176
[6] K. Sakurai, “Quasi-Biennial Variation of the Solar
Neutrino Flux and Solar Activity,” Nature, Vol. 278,
1979, pp. 146-148. doi:10.1038/278146a0
[7] L. J. Lanzerotti and R. S. Raghavan, “Solar Activity and
Solar Neutrino Flux,” Nature, Vol. 293, 1981, pp. 122-
124. doi:10.1038/293122a0
[8] Y. Fukuda, et al., (Kamiokande Collaboration), “Solar
Neutrino Data Covering Solar Cycle 22,” Physical Re-
view Letters, Vol. 77, No. 9, 1996, pp. 1683-1686.
doi:10.1103/PhysRevLett.77.1683
[9] G. A. Bazilevskaya, M. B. Krainev, V. S. Makhmutov, E.
O. Flückiger, A. I. Sladkova and M. Storini, “Structure of
the Maximum Phase of Solar Cycles 21 and 22,” Solar
Physics, Vol. 197, No. 1, 2000, pp. 157-174.
doi:10.1023/A:1026515520311
[10] A. Vecchio and V. Carbone, “On the Origin of the Dou-
ble Magnetic Cycle of the Sun,” The Astrophysical Jour-
nal, Vol. 683, No. 1, 2008, pp. 536-541.
doi:10.1086/589768
[11] J. F. Valdés-Galicia and V. M. Velasco, “Variations of
Mid-Term Periodicities in Solar Activity Physical Phe-
nomena,” Advances in Space Research, Vol. 41, No. 2,
2008, pp. 297-305. doi:10.1016/j.asr.2007.02.012
[12] A. Vecchio, M. Laurenza, V. Carbone and M. Storini,
“Quasi-Biennial Modulation of Solar Neutrino Flux and
Solar and Galactic Cosmic Rays by Solar Cyclic
Activity,” The Astrophysical Journal, Vol. 709, No. 1,
2010, pp. L1-L5. doi:10.1088/2041-8205/709/1/L1
[13] A. Vecchio and V. Carbone, “Spatio-Temporal Analysis
of Solar Activity: Main Periodicities and Period Length
Variations,” Astronomy and Astrophysics, Vol. 502, No. 3,
2009, pp. 981-987. doi:10.1051/0004-6361/200811024
[14] J. F. Valdés-Galicia, R. Pérez-Enríquez and J. A. Otaola,
“The Cosmic-Ray 1.68-Year Variation: A Clue to Under-
stand the Nature of the Solar Cycle?” Solar Physics, Vol.
167, No. 1-2, 1996, pp. 409-417.
doi:10.1007/BF00146349
[15] K. Mursula and J. H. Vilpolla, “Fluctuations of the Solar
Dinamo Observed in the Solar Wind and Interplanetary
Magnetic Field at 1 AU and in the Outer Heliosphere,”
Solar Physics, Vol. 221, No. 2, 2004, pp. 337-349.
doi:10.1023/B:SOLA.0000035053.17913.26
[16] M. Laurenza and M. Storini, “Interpretation of Quasi
Periodic Variations in Solar Cosmic Ray Data,” Pro-
ceedings of the 31st ICRC, ŁÓDŹ, 2009.
[17] M. Laurenza, A. Vecchio, V. Carbone and M. Storini,
“Quasi Biennial Modulation of Galactic Cosmic Rays,”
The Astrophysical Journal, 2012 (in press).
[18] M. Laurenza, M. Storini, S. Giangravé and G. Moreno,
“Search for Periodicities in the IMP8 Charged Particle
Measurement Experiment Proton Fluxes for the Energy
Bands 0.50 - 0.96 MeV and 190 - 440 MeV,” Journal of
Geophysical Research, Vol. 114, No. 1A, 2009.
doi:10.1029/2008JA013181
[19] J. Javaraiah, R. K. Ulrich, L. Bertello and J. E. Boyden,
“Search for Short-Term Periodicities in the Sun’s Surface
Rotation: A Revisit,” Solar Physics, Vol. 257, No. 1,
2009, pp. 61-69. doi:10.1007/s11207-009-9342-9
[20] R. Davis Jr. and J. C. Evans, “Experimental Limits on
Extraterrestrial Sources of Neutrinos,” Proceeding of 13th
International Conference on Cosmic Rays, Vol. 3, 1973,
pp. 2001-2006.
[21] Y. Fukuda, et al., “Measurements of the Solar Neutrino
Flux from Super-Kamiokande’s First 300 Days,” Physical
Review Letters, Vol. 81, No. 6, 1998, pp. 1158-1162.
doi:10.1103/PhysRevLett.81.1158
[22] L. M. Krauss, “Correlation of Solar Neutrino Modulation
with Solar Cycle Variation in p-Mode Acoustic Spectra,”
Nature, Vol. 348, No. 6300, 1990, pp. 403-407.
doi:10.1038/348403a0
[23] J. N. Bahcall and W. H. Press, “Solar-Cycle Modulation
of Event Rates in the Chlorine Solar Neutrino Experi-
ment,” The Astrophysical Journal, Vol. 370, 1991, pp.
730-742. doi:10.1086/169856
[24] D. S. Oakley, H. B. Snodgrass, R. K. Ulrich and T. L.
Vandekop, “On the correlation of solar surface magnetic
flux with solar neutrino capture rate,” The Astrophysical
Journal, Vol. 437, No. 1, 1994, pp. L63-L66.
doi:10.1086/187683
[25] R. L. McNutt Jr., “Correlated Variations in the Solar
Neutrino Flux and the Solar Wind and the Relation to the
Solar Neutrino Problem,” Science, Vol. 270, No. 5242,
1995, pp. 1635-1639. doi:10.1126/science.270.5242.1635
[26] R. M. Wilson, “Correlative Aspects of the Solar Electron
Neutrino Flux and Solar Activity,” The Astrophysical
Journal, Vol. 545, No. 1, 2000, pp. 532-546.
doi:10.1086/317787
[27] P. A. Sturrock, “Solar Neutrino Variability and Its Im-
plications for Solar Physics and Neutrino Physics,” The
Astrophysical Journal Letters, Vol. 688, No. 1, 2008, pp.
L53-L56. doi:10.1086/594993
[28] O. G. Miranda, T. I. Rashba, A. I. Rez and J. W. F. Valle,

L. D’ALESSI ET AL. 56
“Enhanced Solar Antineutrino Flux in Random Magnetic
Fields,” Physical Review D, Vol. 70, No. 11, 2004, Arti-
cle ID: 113002. doi:10.1103/PhysRevD.70.113002
[29] P. Bamert, C. P. Burgess and D. Michaud, “Neutrino
Propagation through Helioseismic Waves,” Nuclear Phy-
sics B, Vol. 513, No. 1-2, 1998, pp. 319-342.
doi:10.1016/S0550-3213(97)00672-X
[30] C. P. Burgess, N. S. Dzhalilov, M. Maltoni, T. I. Rashba,
V. B. Semikoz, M. A. Tórtola and J. W. F. Valle, “Large
Mixing Angle Oscillations as a Probe of the Deep Solar
Interior,” The Astrophysical Journal Letters, Vol. 588, No.
1, 2003, pp. L65-L68. doi:10.1086/375482
[31] C. P. Burgess, N. S. Dzhalilov, T. I. Rashba, V. B.
Semikoz and J. W. F. Valle, “Resonant Origin for Density
Fluctuations Deep within the Sun: Helioseismology and
Magneto-Gravity Waves,” Monthly Notices of the Royal
Astronomical Society, Vol. 348, No. 2, 2004, pp. 609-624.
doi:10.1111/j.1365-2966.2004.07392.x
[32] A. Vecchio, L. D’Alessi, V. Carbone, M. Laurenza and M.
Storini, “The Empirical Mode Decomposition to Study
the Quasi-Biennial Modulation of Solar Magnetic Activ-
ity and Solar Neutrino Flux,” Advances in Adaptive Data
Analysis, Vol. 4, No. 1-2, 2012, Article ID: 1250014.
doi:10.1142/S1793536912500148
[33] L. D’Alessi, A. Vecchio, M. Laurenza, M. Storini and V.
Carbone, “Solar Neutrino Flux Modulated by Solar
Activity,” Proceeding of the International School of
Physics “E. fermi”, Vol. 182: Neutrino Physics and As-
trophysics, IOS Press, Amsterdam, 2012, pp. 349-351.
[34] R. Davis, Private Communications, 2004.
[35] J. N. Abdurashitov, et al., (SAGE Collaboration), “Meas-
urement of the Solar Neutrino Capture Rate with Gallium
Metal. III. Results for the 2002-2007 Data Tacking
Period,” Physical Review C, Vol. 80, No. 1, 2009, Article
ID: 015807, pp. 1-16. doi:10.1103/PhysRevC.80.015807
[36] N. E. Huang, Z. Shen, S. R. Long, M. C. Wu, H. H. Shih,
Q. Zheng, N. C. Yen, C. C. Tung and H. H. Liu, “The
Empirical Mode Decomposition and the Hilbert Spectrum
for Nonlinear and Non-Stationary Time Series Analysis,”
Proceedings of the Royal Society A, Vol. 454, 1998, pp.
903-995. doi:10.1098/rspa.1998.0193
[37] D. A. T. Cummings, R. A. Irizarry, N. E. Huang, T. P.
Endy, A. Nisalak, K. Ungchusak and D. S. Burke, “Trav-
elling Waves in the Occurence of Dengue Haemorrhagic
Fever in Thailand,” Nature, Vol. 427, 2004, pp. 344-347.
doi:10.1038/nature02225
[38] J. Terradas, R. Oliver and J. L. Ballester, “Application of
Statistical Techniques to the Analysis of Solar Coronal
Oscillations,” The Astrophysical Journal, Vol. 614, No. 1,
2004, pp. 435-447. doi:10.1086/423332
[39] D. M. Simpson, A. F. C. Infantosi and D. A. Botero-
Rosas, “Estimation and Significance Testing of Cross-
Correlation between Cerebral Blood Flow Velocity and
Background Electro-Encephalograph Activity in Signals
with Missing Samples,” Medical and Biological Engi-
neering and Computing, Vol. 39, No. 4, 2001, pp. 428-
433. doi:10.1007/BF02345364
[40] S. T. Fletcher, A. M. Broomhall, D. Salabert, S. Basu, W.
J. Chaplin, Y. Elsworth, R. A. Garcia and R. New, “A
Seismic Signature of a Second Dinamo?” The Astrophysi-
cal Journal Letters, Vol. 718, No. 1, 2010, pp. L19-L22.
doi:10.1088/2041-8205/718/1/L19