J. Software Engi neeri n g & Applications, 2010, 3, 944-964
doi:10.4236/jsea.2010.310112 Published Online October 2010 (http://www.SciRP.org/journal/jsea)
Application of Artificial Neural Network, Kriging,
and Inverse Distance Weighting Models for
Estimation of Scour Depth around Bridge Pier
with Bed Sill
Homayoon Seyed Rahman, Keshavarzi Alireza*, Gazni Reza
Water Department, Shiraz University, Shiraz, Iran.
Received July 23rd, 2010; revised August 23rd, 2010; accepted August 25th, 2010.
ABSTRACT
This paper outlines the application of the multi-layer perceptron artificial neural network (ANN), ordinary kriging
(OK), and inverse distance weighting (IDW) models in the estimation of local scour depth around bridge piers. As part
of this study, bridge piers were installed with bed sills at the bed of an experimental flume. Experimental tests were
conducted under different flow conditions and varying distances between bridge pier and bed sill. The ANN, OK and
IDW models were applied to the experimental data and it was shown that the artificial neural network model predicts
local scour depth more accurately than the kriging and inverse distance weighting models. It was found that the ANN
with two hidden layers was the optimum model to predict lo cal scour depth. Th e results from the sixth test case showed
that the ANN with one hidden layer and 17 hidden nodes was the best model to predict local scour depth. Whereas the
results from the fifth te st case found that the ANN with t hree hidden layers was the best model to predi ct local scour depth.
Keywords: Artificial Neural Network, Scour Depth, Ordinary Kriging, Inverse Distance Weighting, Bridge Piers,
Bed Sill
1. Introduction
The accurate estimation of maximum scour depth around
and downstream of bridge piers is critical and very im-
portant for design engineers. The prediction of scour
depth around bridge piers has been the subject of many
experimental studies, and has resulted in a number of
prediction techniques being presented. Scour depth is a
significant limiting factor when assigning the minimum
depth of substructures, as it decreases the lateral capacity
of the substructure.
To determine a technique for predicting scour depth
for different pier positions, comprehensive experimental
tests have been conducted. In the past, a number of re-
search studies had been conducted to determine tech-
niques for the estimation of local scour around bridge
piers and their abutments. These have been reported in
literature. Of these studies, the first extensive experi-
mental work on bridge pier scour was conducted and
reported by Chabert and Engeldinger (1956) which is
cited by Jeng et al. [1]. A study was also conducted by
Blodgett (1978), again is cited by Jeng et al. [1], to report
the cause of failure of 383 bridges. It was reported that
most failures were caused by catastrophic floods. This
study also found that the incorrect prediction of local
scour depth during engineering design lead to enlarged
local and contraction scour. Yankielun and Zabilansky [2]
pointed out that this serious problem costs millions of
dollars worth of damage, leaving foundations of bridge
piers and bridge abutments insecure. Johnson [3] com-
pared some of proposed prediction methods with the
available field data, and concluded that more research is
still required to accurately determine local scour.
To overcome this complicated problem, the artificial
neural network (ANN) was found to be useful as a com-
prehensive function approximator, especially when the
relationship between dependent and independent vari-
ables is inadequately understood [1]. Trent et al. [4,5]
*Present Address: School of Civil & Environmental Engineering, UTS,
Sydney, Australia.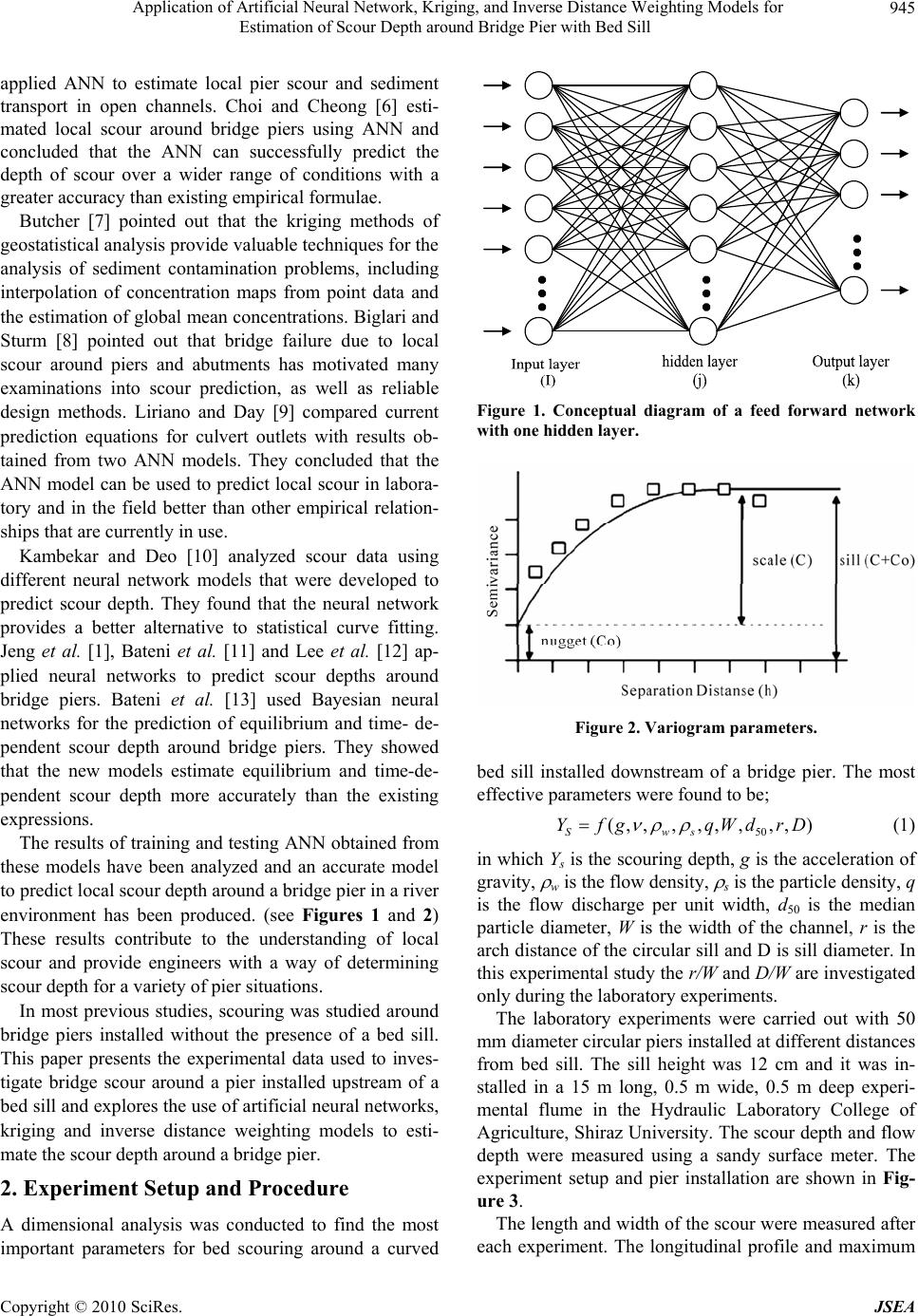

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 945
Estimation of Scour Depth around Bridge Pier with Bed Sill
applied ANN to estimate local pier scour and sediment
transport in open channels. Choi and Cheong [6] esti-
mated local scour around bridge piers using ANN and
concluded that the ANN can successfully predict the
depth of scour over a wider range of conditions with a
greater accuracy than existing empirical formulae.
Butcher [7] pointed out that the kriging methods of
geostatistical analysis prov ide v alu able techniq u es for the
analysis of sediment contamination problems, including
interpolation of concentration maps from point data and
the estimation of global mean concentrations. Biglari and
Sturm [8] pointed out that bridge failure due to local
scour around piers and abutments has motivated many
examinations into scour prediction, as well as reliable
design methods. Liriano and Day [9] compared current
prediction equations for culvert outlets with results ob-
tained from two ANN models. They concluded that the
ANN model can be used to predict local scour in labora-
tory and in the field better than other empirical relation-
ships that are curren tly in use.
Kambekar and Deo [10] analyzed scour data using
different neural network models that were developed to
predict scour depth. They found that the neural network
provides a better alternative to statistical curve fitting.
Jeng et al. [1], Bateni et al. [11] and Lee et al. [12] ap-
plied neural networks to predict scour depths around
bridge piers. Bateni et al. [13] used Bayesian neural
networks for the prediction of equilibrium and time- de-
pendent scour depth around bridge piers. They showed
that the new models estimate equilibrium and time-de-
pendent scour depth more accurately than the existing
expressions.
The results of training and testing ANN obtained from
these models have been analyzed and an accurate model
to predict local scour depth around a bridge pier in a river
environment has been produced. (see Figures 1 and 2)
These results contribute to the understanding of local
scour and provide engineers with a way of determining
scour depth for a variety of pier situations.
In most previous studies, scouring was studied around
bridge piers installed without the presence of a bed sill.
This paper presents the experimental data used to inves-
tigate bridge scour around a pier installed upstream of a
bed sill and explores the use of artificial neural networks,
kriging and inverse distance weighting models to esti-
mate the scour depth around a bridge pier.
2. Experiment Setup and Procedure
A dimensional analysis was conducted to find the most
important parameters for bed scouring around a curved
Figure 1. Conceptual diagram of a feed forward network
with one hidden layer.
Figure 2. Variogram parameters.
bed sill installed downstream of a bridge pier. The most
effective parameters were found to be;
50
(,,,,,,,,)
Sws
Yfg qWdrD



(1)
in which Ys is the scouring depth, g is the acceleration of
gravity,

w is the flow density,

s is the particle density, q
is the flow discharge per unit width, d50 is the median
particle diameter, W is the width of the channel, r is the
arch distance of the circular sill and D is sill diameter. In
this experimental study the r/W and D/W are investigated
only during the laboratory experiments.
The laboratory experiments were carried out with 50
mm diameter circular piers installed at different distances
from bed sill. The sill height was 12 cm and it was in-
stalled in a 15 m long, 0.5 m wide, 0.5 m deep experi-
mental flume in the Hydraulic Laboratory College of
Agriculture, Shiraz University. The scou r depth and flow
depth were measured using a sandy surface meter. The
experiment setup and pier installation are shown in Fig-
ure 3.
The length and width of the scour were measured after
each experiment. The longitudinal profile and maximum

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for
Estimation of Scour Depth around Bridge Pier with Bed Sill
946
Figure 3. Experimental setup and pier installation.
depth of the scour were measured during the experiments.
The scour measured on the side and at the rear of the pier
were approximately the same, whilst the scour measured
at the nose of the pier was less than the back scour.
A false bottom was installed in the flume to create a
recess for the sediment bed. The recess was 2.5 m long,
0.5 m wide and 0.12 m deep and filled with non-cohesive
sediment with 50 equal to 0.5 mm diameter and stan-
dard deviation equal to 1.23 mm. The pier was installed
firstly by preparing an undersized pilot hole, pushing the
pier in, and then trimming off the remaining sediment.
Water entered the flume smoothly from an inlet reservoir,
and a sediment trap was used at the downstream end of
the test reach. Downstream of the trap, water passed over
a tailgate into a sump. Water depth in the in-floor flume
was controlled by a tail gate located at the downstream
end of the test section. All the experiments were con-
ducted under steady flow conditions. The flow discharge
was measured by a 90 degree V-Notch and an electro-
magnetic flow meter.
D
Experimental test cases were conducted in eight dif-
ferent bed sill models (Figure 4). Table 1 explains the
flow condition of the experimental tests.
3. Results and Discussions
3.1. The ANN, OK and IDW Estimations for
Scour around Piers
The whole data set, consisting of 2754 data points, was
composed of eight different conditions. Each condition
was divided into two parts randomly: a training set con-
sisting of 80% of the data points and a validation or test-
ing set consisting of 20% of the data points.
In this study, two types of ANN models were devel-
oped: 1) single hidden-layer ANN model consisting of
only one hidden layer, and 2) multiple hidden-layer ANN
model consisting of two and three hidden layers. The
task of identifying the number of neurons in the input
and output layers is usually simple, as it is dictated by the
input and output variables considered to model the
physical process.
As previously mentioned, the number of neurons in the
hidden layer(s) can be determined thro ugh the us e of trial
and error procedure [1]. The optimal architecture was
determined by varying the number of hidden neurons
(from 1 to 20), and then the best structure was selected.
The training of the ANN models was stopped when ei-
ther the acceptable level of error was achieved or when
the number of iterations exceeded a prescribed maximum
of 2500. The learning rate of 0.05 was also used.
ANN was implemented using the MATLAB software
package (MATLAB version 7.2 with neural network
toolboxes) [14].
The performance of ANN, OK and IDW configura-
tions were assessed based on calculating the mean abso-
lute error (MAE), and the root mean square error
(RMSE). (see Table 2).
The coefficient of determination, of linear re-
gression line, between the predicted values from each
method and the desired output were also used as a meas-
ure of performance. The three statistical parameters used
to compare the performance of the various method con-
2
R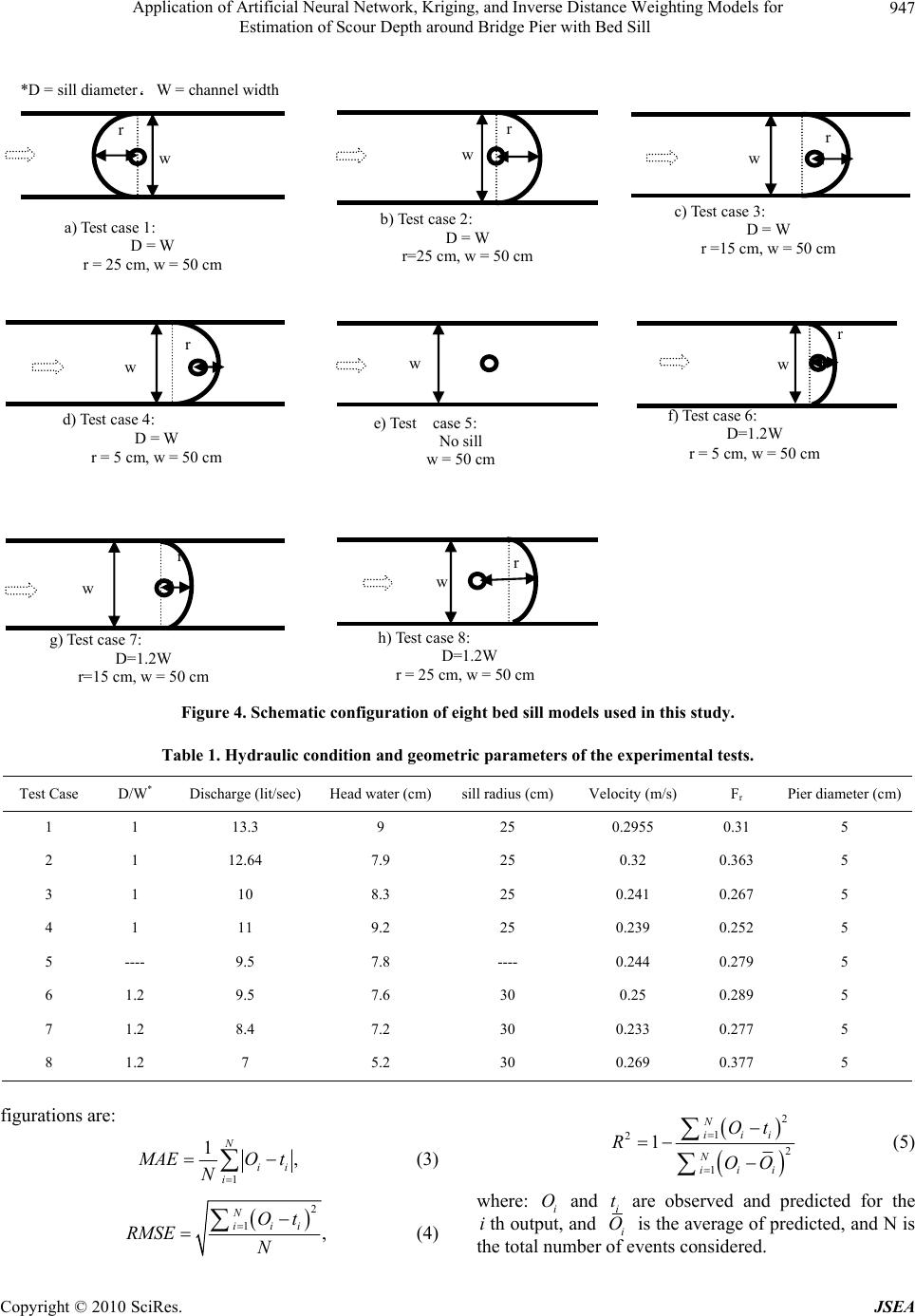

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 947
Estimation of Scour Depth around Bridge Pier with Bed Sill
r
w
a) Test case 1:
D = W
r = 25 cm, w = 50 cm
r
w
b) Test case 2:
D = W
r=25 cm, w = 50 cm
w
c) Test case 3:
D = W
r =15 cm, w = 50 cm
r
w
r
d) Test case 4:
D = W
r = 5 cm, w = 50 cm
w
e) Test case 5:
No si ll
w = 50 cm
r
w
f) Test case 6:
D=1.2W
r = 5 cm, w = 50 cm
r
w
g) Test case 7:
D=1.2W
r=15 cm, w = 50 cm
r
h) Test case 8:
D=1.2W
r = 25 cm, w = 50 cm
w
*D = sill d ia met er، W = channel width
Figure 4. Schematic configuration of eight bed sill models used in this study.
Table 1. Hydraulic condition and geometric parameters of the experimental tests.
Test Case D/W* Discharge (lit/sec) Head water (cm)sill radius (cm) Velocity (m/s) Fr Pier diameter (cm)
1 1 13.3 9 25 0.2955 0.31 5
2 1 12.64 7.9 25 0.32 0.363 5
3 1 10 8.3 25 0.241 0.267 5
4 1 11 9.2 25 0.239 0.252 5
5 - --- 9.5 7.8 - --- 0.244 0.279 5
6 1.2 9.5 7.6 30 0.25 0.289 5
7 1.2 8.4 7.2 30 0.233 0.277 5
8 1.2 7 5.2 30 0.269 0.377 5
figurations are:
1
1,
N
ii
i
M
AEO t
N

 (3)

2
1,
N
iii
Ot
RMSE N

 (4)


2
1
2
2
1
1N
iii
N
iii
Ot
ROO






 (5)
where: i and are observed and predicted for the
th output, and
Oi t
ii O is the average of predicted, and N is
thetotal number of events considered.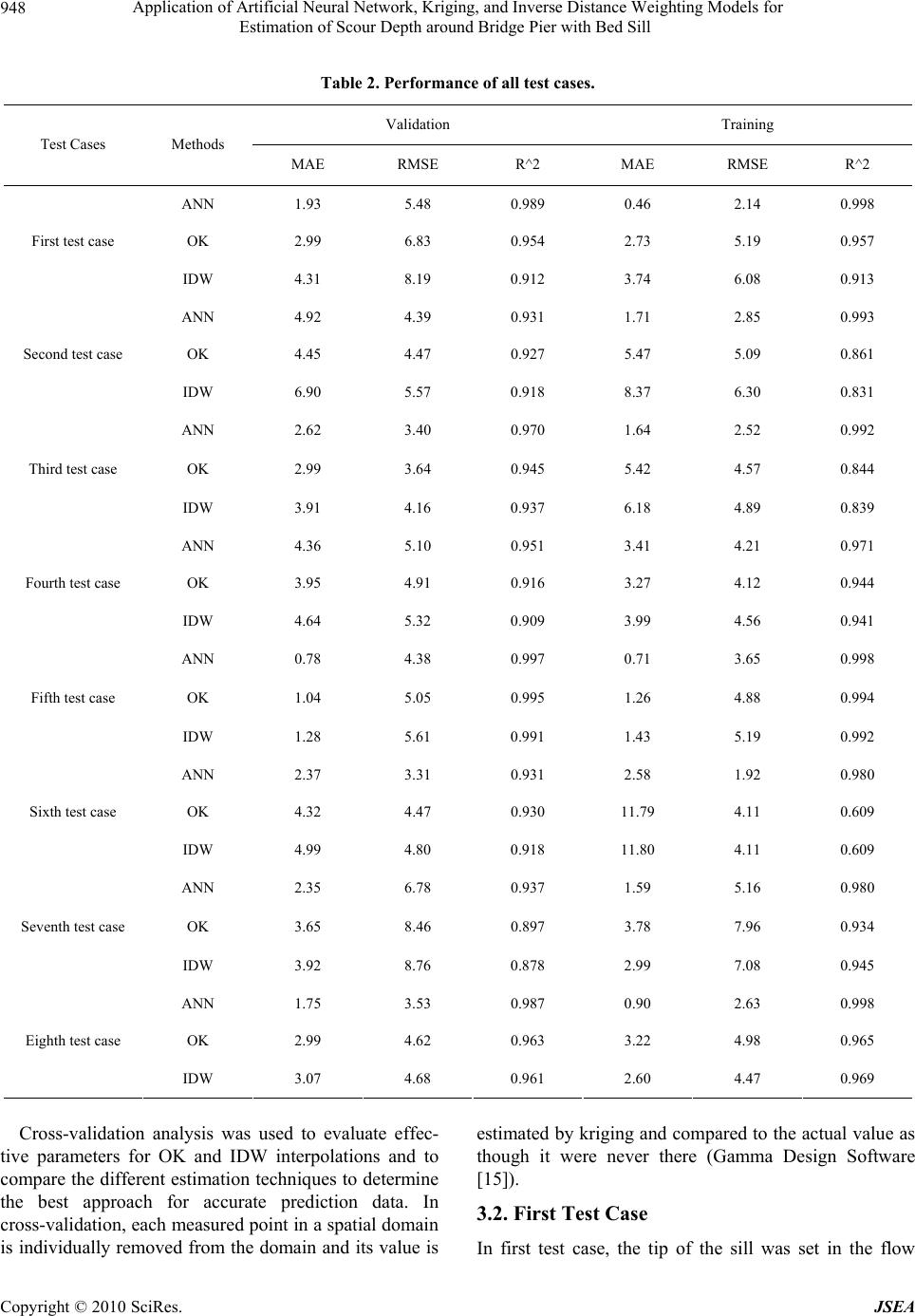

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 948 Estimation of Scour Depth around Bridge Pier with Bed Sill
Table 2. Performance of all test cases.
Validation Training
Test Cases Methods MAE RMSE R^2 MAE RMSE R^2
ANN 1.93 5.48 0.989 0.46 2.14 0.998
OK 2.99 6.83 0.954 2.73 5.19 0.957
First test case
IDW 4.31 8.19 0.912 3.74 6.08 0.913
ANN 4.92 4.39 0.931 1.71 2.85 0.993
OK 4.45 4.47 0.927 5.47 5.09 0.861 Second test case
IDW 6.90 5.57 0.918 8.37 6.30 0.831
ANN 2.62 3.40 0.970 1.64 2.52 0.992
OK 2.99 3.64 0.945 5.42 4.57 0.844 Third test case
IDW 3.91 4.16 0.937 6.18 4.89 0.839
ANN 4.36 5.10 0.951 3.41 4.21 0.971
OK 3.95 4.91 0.916 3.27 4.12 0.944 Fourth test case
IDW 4.64 5.32 0.909 3.99 4.56 0.941
ANN 0.78 4.38 0.997 0.71 3.65 0.998
OK 1.04 5.05 0.995 1.26 4.88 0.994 Fifth test case
IDW 1.28 5.61 0.991 1.43 5.19 0.992
ANN 2.37 3.31 0.931 2.58 1.92 0.980
OK 4.32 4.47 0.930 11.79 4.11 0.609 Sixth test case
IDW 4.99 4.80 0.918 11.80 4.11 0.609
ANN 2.35 6.78 0.937 1.59 5.16 0.980
OK 3.65 8.46 0.897 3.78 7.96 0.934 Seventh test case
IDW 3.92 8.76 0.878 2.99 7.08 0.945
ANN 1.75 3.53 0.987 0.90 2.63 0.998
OK 2.99 4.62 0.963 3.22 4.98 0.965 Eighth test case
IDW 3.07 4.68 0.961 2.60 4.47 0.969
Cross-validation analysis was used to evaluate effec-
tive parameters for OK and IDW interpolations and to
compare the different estimation techniques to determine
the best approach for accurate prediction data. In
cross-validation, each measured point in a spatial domain
is individually removed from the domain and its value is
estimated by kriging and compared to th e actual value as
though it were never there (Gamma Design Software
[15]).
3.2. First Test Case
In first test case, the tip of the sill was set in the flow

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 949
Estimation of Scour Depth around Bridge Pier with Bed Sill
direction (in the shape of a convex) and a space of 25 cm
was set between the sill and bridge pier. The diameter of
the sill is equal to the flume width.
In ANN prediction, optimal architecture is determined
by varying the number of hidden neurons (from 1 to 20),
and the best structure is selected. It was found that the
most accurate results involved use of the feed forward
back propagation with two hidden layers and an archi-
tecture of configuration: 2-7-4-1.
To evaluate the performance of the ANN, OK and
IDW, observed local scour depth values are plotted
against the predicted values. Figure 5 illustrates the re-
sults with the performance indices between predicted and
observed data for the training and testing data sets, re-
spectively.
Figures 5(c-f) also exhibit that kriging has a lower
training error compared with IDW, and its validation
error becomes lower than IDW. In other words, kriging
validation results have a lower scatter than IDW. As it
can be seen from Figure 5(a-b), ANN has performed
well in predicting the local sco ur depth.
Comparing ANN results with those of OK and IDW it
is found that ANN has the lowest training error and vali-
dation error, then kriging and IDW. Also interpolated
local scour maps (Figure 6) show that the interpolated
map of the ANN model is more similar to the interpo-
lated map of the observation map as compared with the
interpolated map of kriging and IDW.
3.3. Second Test Case
In the second test case, the bed sill was set in the flow
direction (in the shape of a concave) and spaces of 25cm
were set between the bridge pier and bed sill. Figure 7
illustrates the results with the performance indices be-
tween predicted and observed data for the training and
testing data sets, respectively.
When the methods were compared, the training accu-
racy was significant. It is observed that all models per-
form with poor accuracy in comparison with results of
the first data set. Comparison between these three valida-
tions of evaluating scour depth in all runs for ANN, OK
and IDW revealed that the difference in accuracy be-
tween those was not significant. Also the accuracy of
training in OK and IDW was less than the validation. It is
shown that these methods are not reliable in this condi-
tion because it cannot predict the training data well. In
this condition, the ANN model performed well and the
IDW had the lowest accuracy. The interpolated maps are
demonstrated in Figure 8.
3.4. Third Test Case
In a similar manner, the third condition data was used to
predict local scour depth with ANN, OK and IDW. In
this third test case, similar to second test, the bed sill was
set in the flow direction but the distance between the
bridge pier and bed sill was set to 15 cm.
Figure 9 shows the results with the performance indi-
ces between predicted and observed data for the training
and testing data sets, respectively. Again, the ANN
model performs well in training and validation. The ac-
curacy of prediction was not considerably different be-
tween OK and IDW and as it is shown in Figure 10. The
interpolated map of observation data, ANN, OK and
IDW for the third test case is shown in Figure 10.
Accuracy of training was more than validation in the
ANN prediction, whereas in the two other mentioned
methods, correctness of training was less than the valida-
tion. In other words, the results of the OK and IDW were
not as precise as for ANN. The accuracy in training of
ANN was more reliable when compared with OK and
IDW methods.
3.5. Fourth Test Case
The fourth test case was similar to second test, but the
distance between bridg e pier and bed sill was set to 5cm.
From ANN prediction, the best structure was found to be
a configuration of 2-4-4-1.
Figure 11 shows the results with the performance in-
dices between predicted and observed data for the train-
ing and testing data sets, respectively.
The three interpolated maps of the aforementioned
methods are very similar (Figure 12) and comparison
between these three training and validations for evaluat-
ing scour depth in all runs for ANN, OK and IDW re-
vealed that the difference in accuracy between them was
not significant.
3.6. Fifth Test Case
In the fifth test case the bridge pier was set separately in
the flume. From ANN estimates, unlike the previous four
conditions, the best result was obtained for a 2-4-4-4-1
structure.
The comparison between these three training and
validations for evaluating scour depth in all runs for
ANN, OK and IDW revealed that the difference in accu-
racy between these was not significant (Figure 13). It
was found that the ANN accuracy was better than other
methods.
This test was similar to the fourth test where the three
interpolated maps of the methods were very similar to
interpolated map of observed data (Figure 14).
3.7. Sixth Test Case
This experiment was similar to the second test case,

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for
Estimation of Scour Depth around Bridge Pier with Bed Sill
950
(a) (b)
(c) (d)
(e) (f)
Figure 5. Performance of ANN, OK and IDW for the first test case: (a) ANN Validation; (b) ANN Training; (c) OK Valida-
tion; (d) OK Cross Validation; (e) IDW Validation; (f) IDW Cross Validation.

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 951
Estimation of Scour Depth around Bridge Pier with Bed Sill
Figure 6. Interpolated maps of observed data, ANN, OK and IDW test for first test case.
(a) (b)

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 952 Estimation of Scour Depth around Bridge Pier with Bed Sill
(c) (d)
(e) (f)
Performance of ANN of first test case (convex type); (a) testing, (b) training
Figure 7. Performance of ANN, OK and IDW for the 2nd test case: (a) ANN Validation; (b) ANN Training; (c) OK Valida-
tion; (d) OK Cross Validation; (e) IDW Validation; (f) IDW Cross Validation.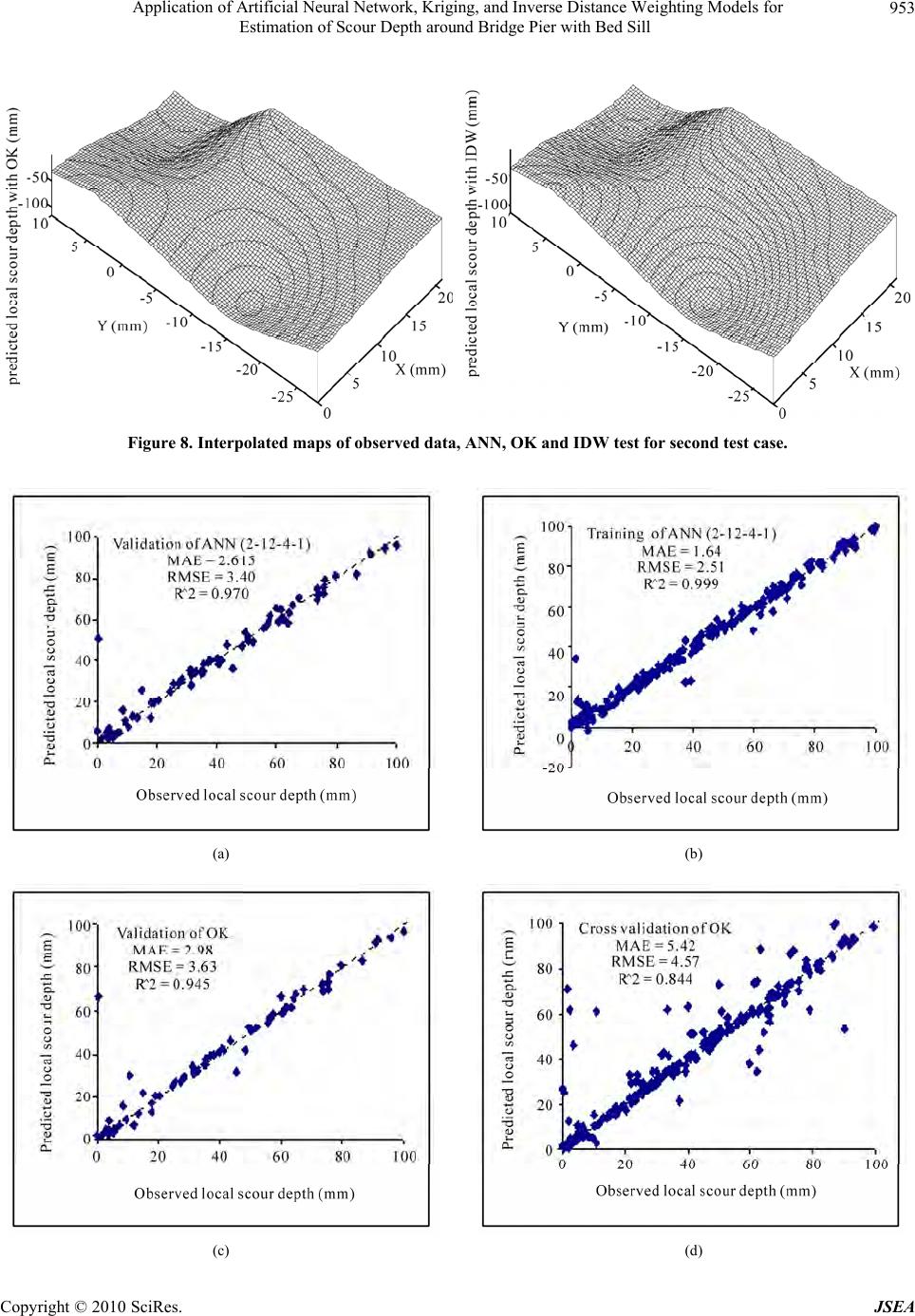

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 953
Estimation of Scour Depth around Bridge Pier with Bed Sill
Figure 8. Interpolated maps of observed data, ANN, OK and IDW test for second test case.
(a) (b)
(c) (d)

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 954 Estimation of Scour Depth around Bridge Pier with Bed Sill
(e) (f)
Figure 9. Performance of ANN, OK and IDW for the third test case: (a) ANN Validation; (b) ANN Training; (c) OK Valida-
tion; (d) OK Cross Validation; (e) IDW Validation; (f) IDW Cross Validation.
Figure 10. Interpolated maps of observed data, ANN, OK and IDW test for third test case.

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 955
Estimation of Scour Depth around Bridge Pier with Bed Sill
(a) (b)
(c) (d)
(e) (f)
Figure 11. Performance of ANN, OK and IDW for the fourth test case: (a) ANN Validation; (b) ANN Training; (c) OK Vali-
dation; (d) OK Cross Validation; (e) IDW Validation; (f) IDW Cross Validation.

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 956 Estimation of Scour Depth around Bridge Pier with Bed Sill
Figure 12. Interpolated maps of observed data, ANN, OK and IDW test for fourth test case.
(a) (b)

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 957
Estimation of Scour Depth around Bridge Pier with Bed Sill
(c) (d)
(e) (f)
Figure 13. Performance of ANN, OK and IDW for the fifth test case: (a) ANN Validation; (b) ANN Training; (c) OK Valida-
tion; (d) OK Cross Validation; (e) IDW Validation; (f) IDW Cross Validation.

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 958 Estimation of Scour Depth around Bridge Pier with Bed Sill
Figure 14. Interpolated maps of observed data, ANN, OK and IDW test for fifth test case.
(a) (b)
(c) (d)

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 959
Estimation of Scour Depth around Bridge Pier with Bed Sill
(e) (f)
Figure 15. Performance of ANN, OK and IDW for the sixth test case: (a) ANN Validation; (b) ANN Training; (c) OK Valida-
tion; (d) OK Cross Validation; (e) IDW Validation; (f) IDW Cross Validation.
Figure 16. Interpolated maps of observed data, ANN, OK and IDW test for sixth test case.

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 960 Estimation of Scour Depth around Bridge Pier with Bed Sill
(a) (b)
(c) (d)
(e) (f)
Figure 17. Performance of ANN Training; (c) OK Vali- NN, OK and IDW for the seventh test case: (a) ANN Validation; (b) A
dation; (d) OK Cross Validation; (e) IDW Validation; (f) IDW Cross Validation.

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 961
Estimation of Scour Depth around Bridge Pier with Bed Sill
Figure 18. Interpolated maps of observed data, ANN, OK and IDW test for seventh test case.
(a) (b)

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for
Estimation of Scour Depth around Bridge Pier with Bed Sill
962
(c) (d)
(e) (f)
Figure 19. Performance of ANali-
similar to the third case, how-
N, OK and IDW for the eighth test case: (a) ANN Validation; (b) ANN Training; (c) OK V
dation; (d) OK Cross Validation; (e) IDW Validation; (f) IDW Cross Validation.
however the diameter of bed sill was equal to 1.2 times
the channel width.
From ANN prediction, the optimal architecture was
determined by varying the number of hidden neurons
(from 1 to 20), and the best structure w as selected. It was
found that best structure has only one hidden layer and
its architecture has the configuration of 2-17-1.
Figure 15 shows training and validation results, re-
spectively. Again, the ANN model performs much better
in training and validation. In OK and IDW the accuracy
of training is less than validation, but OK showed the
best results after ANN. An interpolated map of ANN
(Figure 16) conforms to the interpolated map of ob-
served local scour depth but the OK and IDW interpo-
lated maps are not matched to the observed interpolated
map.
3.8. Seventh Test Case
This seventh test case was
ever the diameter of bed sill was equal to 1.2 times the
flume width.
From ANN prediction the best structure was selected.
It was found that the most accurate results involved use
of configuration 2-7-4-1.
Figure 17 depict training and validation results sepa-
rately for ANN, OK and IDW, respectively, for the sev-
enth data set. When these methods are compared, it was
shown that ANN had the best accuracy and IDW had a

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 963
Estimation of Scour Depth around Bridge Pier with Bed Sill
Figure 20. Interpolated maps of observed data, ANN, OK and IDW test for eighth test case.
w accuracy. Comparisons between these three interpo-
e bed sill was set in the flow
or Prediction of
In accurate of the three pre-
sented methods, Table 1 represents the results of the
the application of artificial neural
mely the multi-layer perceptron, the
The results of this study showed that the ANN model
lo
lated maps show that the interpolated map of ANN is
very similar to the interpolated map of observed local
scour depth (se e Figure 18).
3.9. Eighth Test Case
In the eighth test case, th
direction with a distance of 25cm between the bridge pier
and bed sill. From ANN prediction the best structure was
selected. It was found that the most accurate results in-
volved the use of a configuration 2-12-4-1. In the esti-
mate from this test case, like the last seven estimates,
ANN has better results when compared with the other
methods (Figure 19) and the difference in accuracy be-
tween OK and IDW isn’t significant, as confirmed by the
interpolated maps (Figure 20).
4. Appropriate Methods f
Local Scour Depth
order to identify the most
research for all conditions. For all conditions, the ANN
has the best accuracy in training and validation. ANN
performance shows significant preciseness under every
condition for th e predictio n of local scour depth. Only in
the fifth test case, the difference in accuracy was very
close for all methods. Performance of OK reveals good
accuracy, but it has lower precision when compared with
the ANN performance. In OK and IDW, accuracy of
training is almost the same but OK has better precision in
validation performance. Consequently, IDW shows lower
performance over all conditions.
5. Conclusions
This paper outlines
network (ANN), na
ordinary kriging (OK) and the inverse distance weighting
(IDW) models in the estimation of local scour depth
around bridge piers where bed sills have been installed.

Application of Artificial Neural Network, Kriging, and Inverse Distance Weighting Models for 964 Estimation of Scour Depth around Bridge Pier with Bed Sill
A
rk that includes one hidden layer and 17 hidden
no
Neural Network
Assessment for Scour Depart-
ment of Civiersity of Sydney
, San Fran-
eural Networks,”
Local Scour
porate Screening Data:
glary and T. W. Sturm, “Numerical Modeling of
d R. A. Day, “Prediction of Scour Depth
n of Group
, “Neural Net-
eu-
B. W. Melville, “Bayesian
Neural Network Toolbox for Use with
urfer Contouring and
gives more accurate local scour depth predictions than
the existing methods. As such, it is recommended that the a
NN model be used for local scour depth predictions
instead of the kriging and inverse distance weighting
models.
The ANN with two hidden layers was selected as the
optimum network to predict local scour depth, whereas
the netwo
Hud
des within that layer was the best model to predict
local scour depth as it is shown in the sixth test case with
D/W = 1.2 and r = 5 cm. Also three layer s was found the
best model to predict local scour depth for test case with
no sill as it is shown in the fifth test case.
REFERENCES
[1] D. S. Jeng, S. M. Bateni and E. Lockett, “
,
Pi
th Around Bridge,” Dep
l Engineering, the Univ
Sydney, NSW, Australia, Environmental Fluids/Wind
Group, Res earch Report No R8 55, 2006.
[2] N. E Yankielun and L. Zabilansky, “Laboratory Investi-
gation of Time-Domain Reflectometry System for Moni-
toring Bridge Scour,” Journal of Hydraulic Engineering,
ASCE, Vol. 125, No. 12, 1999, pp. 1279-1284.
[3] P. A. Johnson, “Comparison of Pier-Scour Equations
Using Field Data,” Journal of Hydraulic Engineering,
ASCE, Vol. 121, No. 8, 1995, pp. 626-629.
[4] R. Trent, N. Gagarain and J. Rhodes, “Estimating Pier
Scour with Artificial Neural Networks,” Proceedings of
ASCE Conference on Hydraulic Engineering
cisco, CA, 1993a, pp. 1043-1048.
[5] R. Trent, A. Molinas and N. Gagarain, “An Artificial
Neural Networks for Computing Sediment Estimation of
Scour Below Spillways Using N Pro-
ceedings of ASCE Conference on Hydraulic Engineering,
San Francisco, CA, 1993b, pp. 1049-1054.
[6] S. Choi and S. Cheong, “Prediction of
round Bridge Piers Using Artificial Neural Networks,”
Journal of the American Water Resources Association,
Vol. 42, No 2, 2006, pp. 487-494.
[7] J. B. Butcher, “Co-kriging to Incor
son River Sediment,” Journal of the American Water
Resources Association, Vol. 32, No. 2, 1996, pp. 349-
356.
[8] B. Bi
Flow around Bridge Abutments in Compound Channel,”
Journal of Hydraulic Engineering, ASCE, Vol. 124, 1998,
pp. 156-164.
[9] S. L. Liriano an
at Culvert Outlets Using Neural Networks,” Journal of
Hydroinformatics, Vol. 3, 2001, pp. 231-238.
[10] A. R. Kambekar and M. C. Deo, “Estimatio
le Scour Using Neural Networks,” Applied Ocean Re-
search, Vol. 25, No. 4, 2003, pp. 225-234.
[11] S. M. Bateni, S. M. Borghei and D. S. Jeng
work and Neuro-Fuzzy Assessments for Scour Depth
around Bridge Piers,” Engineering Applications of Artifi-
cial Intelligence, Vol. 20, No. 3, 2007a, pp. 401-414.
[12] T. L. Lee, D. S. Jeng, G. H. Zhang and I. H. Hong, “N
ral Network Modeling for Estimation of Scour Depth
around Bridge Piers,” Journal of Hydrodynamic, Vol. 19,
No. 3, 2007, pp. 378-386.
[13] S. M. Betani, D. S. Jeng and
Neural Networks for Prediction of Equilibrium and
Time-Dependent Scour Depth around Bridge Piers,” Ad-
vances in Engineering Software, Vol. 38, No. 2, 2007b,
pp. 102-111.
[14] Mathworks, “
MATHLAB,” User’s Guide, th e MathWorks, Inc., N a-
tick, MA, 2006, pp. 2-1 to 3-36.
[15] Golden Software User’s guide, “S
3D Surface Mapping for Scientists and Engineers,” 8th
Edition, Golden Software, Inc., Golden, CO, 2002.