Paper Menu >>
Journal Menu >>
 Psychology, 2010, 1, 252-260 doi:10.4236/psych.2010.14034 Published Online October 2010 (http://www.SciRP.org/journal/psych) Copyright © 2010 SciRes. PSYCH A Mathematical Study of the Dynamics of Conscious Acquiring of Knowledge through Reading and Cramming and the Process of Losing Information from the Brain by Natural Forgetting of Facts Sudipto Roy1, Priyadarshi Majumdar2 1Department of Physics, Calcutta Institute of Engineering and Management, Kolkata, India; 2Jyotinagar Bidyasree Niketan H.S. School, Kolkata, India. Email: sr_ciem@rediffmail.com, majumdar_priyadarshi@yahoo.com Received May 29th, 2010; revised June 17th, 2010; accepted August 23rd, 2010. ABSTRACT We model the conscious learning process of human brain with a dynamical equation (cramming dynamics) by consid- ering both the data entry and loss of data simultaneously. We show the analytical solution of the differential equation in some special cases. We define some indexes like memory index, merit index, utilization index etc. Using them we can measure the corresponding memory functions. Applications of this model have also been discussed. More general nu- merical and analytical results are also presented at the end. Keywords: Switching Function, Cramming Dynamics, Memory Index, Merit index, Utilization Index, Relative Performance Index 1. Introduction The memory retention mechanism in human brain is quite a complicated process indeed. It is just like infor- mation processing for a huge database. This database is filled with all sorts of information that we use to go about our everyday lives. The information is stored and re- trieved as needed. No matter what we are doing, at any instant or other, at anywhere, the memory is involved in an active fashion. This complex system or network of data processing is located in different parts of the brain like the hippocampus and cortex. As these parts work in tandem, memory begins to process and interacts with the environment and its surroundings. After understanding how we process memory, why do we sometimes loose memories? It has been proven that we forget simply because of a problem with encoding, storage, retrieval, or a combination of any of these. The first significant study in this field was carried out by Ebbinghaus [1]. He studied the memorisation of non- sense syllables. By repeatedly testing himself after va- rious time periods and recording the results, he was the first to describe the shape of the forgetting curve. On the other hand acording to Eichenbaum [2], most forgetting occurs very soon after learning. However, when mean- ingful material is used, the forgetting curve is not so steep. Memory also fades and become less reliable with time and aging. An over flow of information may also cause certain information to be forgotten as a result of competition. Benfen ati [3] in his work examined the cel- lular and molecular mechanisms that contribute to the various forms of memory including short and long-term memory, unconscious and conscious memory etc. Cro- vitz et al. [4] suggested that a memory measurement (M) can be expressed as a power function of time t as, M t . Anderson [5] mentioned that the experimen- tal power function curves are related to the mean taken over all the subjects. Wixted [6] opposed the idea of Anderson by showing that the power function also fits better than the exponential function when data from the individual subjects are fitted. Other important models of the forgetting process are CHARM, due to Metcalfe [7],  A Mathematical Study of the Dynamics of Conscious Acquiring of Knowledge Through Reading and Cramming and the Process of Losing Information from the Brain by Natural Forgetting of Facts Copyright © 2010 SciRes. PSYCH 253 Chappell [8], Matrix Model, due to Humphreys [9] and MINERVA II due to Hintzman [10]. The neural network model predicted by Hopfield [11] was latter modified by sikstrom [12] using the concept of bounded weights and a distribution of learning rates. In a recent communica- tion Stepanov [13] proposed a new model of memoriza- tion dynamics using exponential functions. In our work we have attempted to build up a physical model of the memorizing process of the human brain (of a learner in particular) undergoing a course of study with a fixed duration of time. The act of learning is considered here as a process of data storage in the brain. It is as- sumed that one accumulates data while studying a sub- ject consciously and there is a continuous process of data loss, caused by several physiological and psychological factors such as mental stress and fatigue etc. As this memorizing and forgetting processes are continuous in the said time interval hence we can express this process as a dynamical equation to be explained in more details in the section to follow. The dynamical equation inv olves different parameters quantifying the capacity of the brain from different aspects e.g. memorization ability, grasping power etc. The solution to that differential equation of learning process gives us a clear picture of how data are being stored and lost continuously from the brain. We have obtained the analytical solution of the said equation in some particular limits and the numerical solution has also been obtained as a result of system simulation using MATLAB in Intel platform. The corresponding results are mentioned in the sections to follow. The idea behind choosing this particular model of the brain and the basic assumptions are very simple and based upon our common experiences. We have assumed that the rate of data storage (accumulation rate) in the brain at any instant can be calculated simply by subtract- ing the rate of data loss from the rate of data entry. Ob- viously the actual dynamics of the brain may not be ex- actly the same as we have assumed but for all practical purposes our work can mimic the activity of the br ain up to a certain extent that will be cleared from our next analysis. To support this claim we have shown that the work of Ebbinghaus [1] will come as a special case of our model. Also none of the previous models as men- tioned earlier are as so much simple like ours and can give a complete mathematical description of both the learning and forgetting processes simultaneously using the concept of switchin g process of the brain. 2. Mathematical Modeling Let RS, RL and RE be the rate of data storage, the rate of data loss and the rate of data entry in the brain at any instant respectively. Let x(t) be the amount of data or information already stored in the brain at any time t, hence, the rate of storage at that moment is given by SEL dx RRR dt (1) The rate of data entry can be enhanced by the factors like intelligence, concentration, the ability of a person to cope with the stressed situations etc. Experience tells us that as we go on acquiring more and more knowledge and thereby store more and more data, the rate of data entry becomes slower due to some mental stress or brain fatigue, as we generally perceive. As the accumulated data increases in volume in the brain, the rate of data entry must decrease. Hence, to give it a very simple mathematical form, one can safely assume that at any point of the learning process we have () on E E RStR. (2) where ()St is a time dependent switching function (to be discussed elaborately later on) whose value toggles between 0 and 1 for it’s OFF and ON stages respectively. During a conscious effort of cramming, this switch rem- ains ON and otherwise it is OFF. on E R is actually the rate of data entry for the ON state of the switch ()St . Thus, during the ON state, we have on EE RR. During the OFF state of ()St we have0 E R. We define on E R as Equation (3). Here, C1 quantifies one’s intelligence, concentration, eagerness, urgency of learning etc. Thus, it is a measure of the traits of the learner that causes faster entry of data. C denotes the maximum storage capacity, hence x C . The quantity / x C is the fraction of memory occupied by information and therefore (1/ ) x C is the fraction of storage space still available for data entry. Common experience tells us that, larger the va lue of / x C, greater will be the difficulty in the further storage of data. The parameter is a positive quantity that may be called the index of brain fatigue related to memorization (taking care of the non-linearity). Since 1 x C is generally a fraction, E on R is smaller for larger values of . 11 1 1 1/ on E C measure of grasping power, concentration, IQ and urgency of learningx R C measure of factorsimpedingaccumulation ofdataC xC (3)  A Mathematical Study of the Dynamics of Conscious Acquiring of Knowledge Through Reading and Cramming and the Process of Losing Information from the Brain by Natural Forgetting of Facts Copyright © 2010 SciRes. PSYCH 254 It is a common experience that one forgets information more rapidly when the amount of accumulated data is large. In mathematical terms, the larger the value of / x C, greater will be the amount of data loss per unit time. As the storage becomes higher the rate of loss bec- omes more and more pronounced, possibly due to the limitation of retention ab ility and the stress caused by the load of already accumulated data. One may simply write an expression for rate of data loss (RL), at any stage of learning, as a function of the data (x) already stored in the brain in the following way 2 β L x /C stress caused by data storage or data load Rmemory retention abilityC (4) The parameter C2 is a measure of one’s ability of memory retention or memorizing ability. The term (/ ) x C may be regarded as a measure of stress caused by the accumulated data where the parameter is int- roduced to take care of the natural non-linearity of the process. Like , it is also a positive quantity. Since (/ ) x C is a fraction , L R is smaller for higher values o f . The parameter may be called the stress endur- ance index. A person with a larger value of feels less stressed by the accumulated data (i.e. less internal anxi- ety about the necessity of retention of accumulated data). With substitutions in (1), from (2, 3) and (4) we have 12 (/ ) () 1 dxxx C StC dtC C (5) Let us define a dimensionless variable as/ X xC (with X varying from 0 to 1). Hence, in terms of X, (5) can be expressed as 1 2 () 1 StC dX X X dt CCC (6) 3. Analysis For any arbitrary learner the parameters C1 and C2 are defined below max 111 1 , where 01,CfC f (7) max 222 2 , where 01,CfC f (8) Here, max 1 C and max 2 Care the values of 1 C and 2 Cfor the best possible learner (ideal, being the most intelligent, enthusiastic, diligen t and having the strongest memory and greatest zeal for learning). Here, we define the dimensionless parameters 12 and ff as the merit index and the memory index respectively of any arbitrary learner, quantifying one’s IQ and MRA (memory reten- tion ability) respectively, relative to the best learner. For the learner of the highest calibre or merit we have 12 1ff . Using (7) and (8) in (6) we obtain max 11 max 22 () 1 St fC dX X X dt CCf C (9) For convenience of calculation (without any loss of generality) we may choose max max 12 1CC. If a system of units can be defined for these quantities, they can al- ways be chosen to satisfy this equality. Hence (9) can be expressed as 1 2 () 1 St f dX X X dt CCf (10) To determine the variation of X as a function of time, we need to solve (10) for different functional forms of()St (Figures 1-3). Where()St is a function determining the duration for which the data entry channel remains open. As long as one maintains a conscious learning effort, ()St remains 1, zero otherwise. During the time when () 0St we have from (10) 2 dX X dt Cf (11) Let m T be the duration for which one maintains a conscious memorizing effort without any break. Hence we may write ()1 for 0m Stt T (12) ()0 for m Stt T (13) The above criteria can very well be approximated by a tan-hy perbolic function as gi ven below 1 ()1tanh ()1 2m Stt T (14) Figure 1. Variation of X with t for three different values of C, with 12 0.6 0.6 f =, f =, 6 10 , 200 m T, 0.9α, 25β and S(t) follows (14). 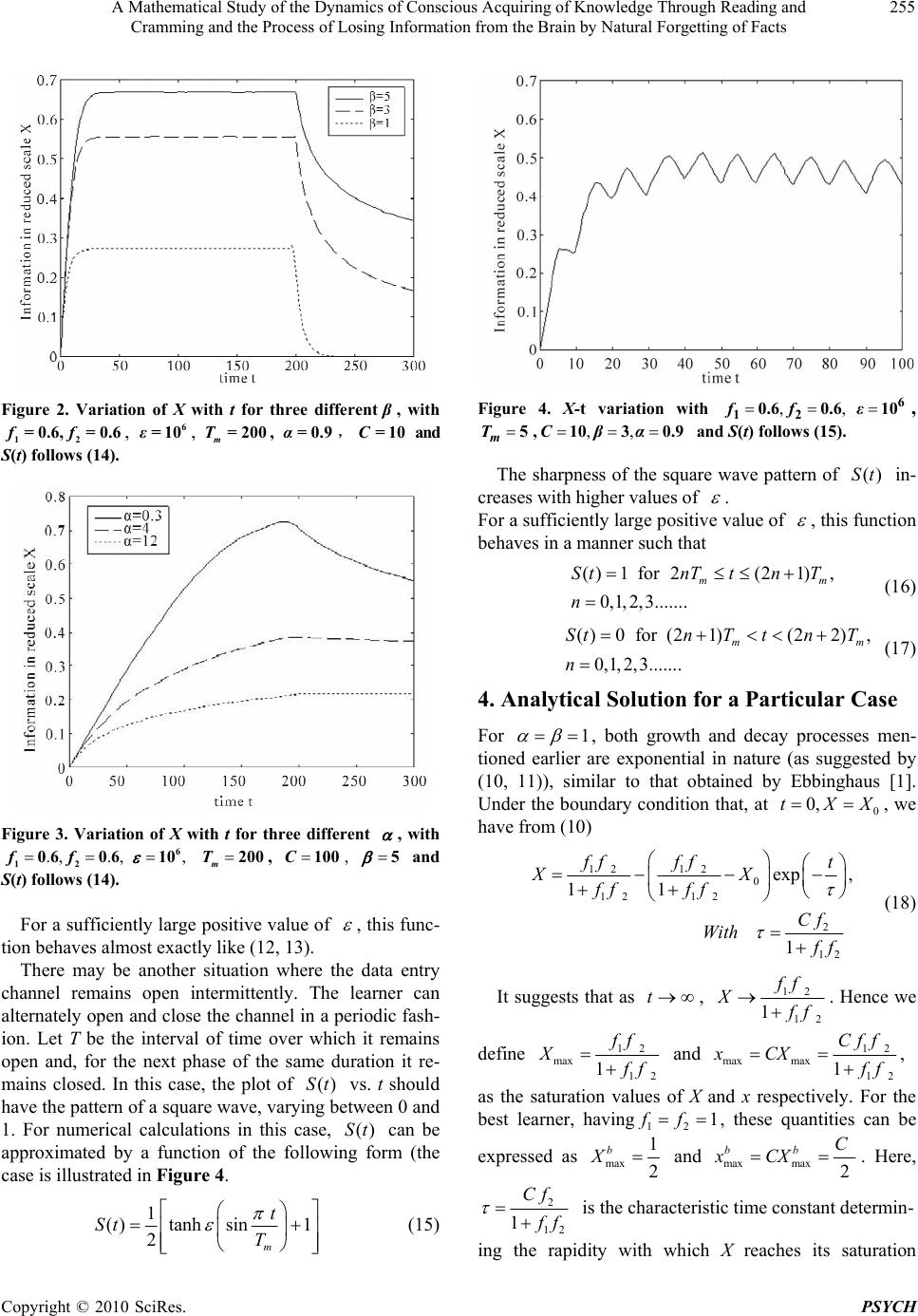 A Mathematical Study of the Dynamics of Conscious Acquiring of Knowledge Through Reading and Cramming and the Process of Losing Information from the Brain by Natural Forgetting of Facts Copyright © 2010 SciRes. PSYCH 255 Figure 2. Variation of X with t for three different β , with 12 0.6, 0.6f=f= , 6 10ε=, 200 m T= , =0.9α, =10C and S(t) follows (14). Figure 3. Variation of X with t for three different , with ., ., 12 06 06ff ,6 10 200 m T, 100C, 5 and S(t) follows (14). For a sufficiently large positive valu e of , this func- tion behaves almost exactly like (12, 13). There may be another situation where the data entry channel remains open intermittently. The learner can alternat ely open and close th e channel in a period ic fash- ion. Let T be the interval of time over which it remains open and, for the next phase of the same duration it re- mains closed. In this case, the plot of ()St vs. t should have the pattern of a square wave, varying between 0 and 1. For numerical calculations in this case, ()St can be approximated by a function of the following form (the case is illustrated in Figure 4. 1 ()tanh sin1 2m t St T (15) Figure 4. X-t variation with ,, 12 0.6 0.6ff 6 10ε, 5 m T,,, 103 0.9Cβα and S(t) follows (15). The sharpness of the square wave pattern of ()St in- creases with higher values of . For a sufficiently large positive value of , this function behaves in a manner such that ()1 for 2(21), 0,1,2,3....... mm StnT tnT n (16) ()0 for (21)(22), 0,1,2,3....... mm StnT tnT n (17) 4. Analytical Solution for a Particular Case For 1 , both growth and decay processes men- tioned earlier are exponential in nature (as suggested by (10, 11)), similar to that obtained by Ebbinghaus [1]. Under the boundary condition that, at 0 0,tXX, we have from (10) 1212 0 12 12 2 12 exp , 11 1 ff fft XX ff ff Cf With ff (18) It suggests that as t, 12 12 1 ff Xff . Hence we define 12 max 12 1 ff Xff and 12 max max12 1 Cf f xCX ff , as the saturation values of X and x respectively. For the best learner, having12 1ff , these quantities can be expressed as max 1 2 b X and maxmax 2 bb C xCX . Here, 2 12 1 Cf ff is the characteristic time constant determin- ing the rapidity with which X reaches its saturation  A Mathematical Study of the Dynamics of Conscious Acquiring of Knowledge Through Reading and Cramming and the Process of Losing Information from the Brain by Natural Forgetting of Facts Copyright © 2010 SciRes. PSYCH 256 value max X. For smaller values of , X varies at a faster rate with time. For 12 1ff, we have max 2 C . The duration (m T) of the interval, for which one continues a conscious cramming effort, may be expressed as a multiple of max as max 2 m NC TN . Hence. 2 12 2 (1 ) m Tf Nff (19) Let us now define a dimensionless variable n such th at m tnT (20) Combining (19) and (20) we obtain 12 2 (1 ) 2 nNf f t f (21) Incorporating all these results in (18) we get the foll- owing expression of X representing the data storage process up to the time of m tT we are getting 1 maxmax 0max () exp 2 m nNf Xt TXXXX (22) While studying the behaviour of X beyond m tT , we need to solve (10) for 1 and ()0St under the boundary condition that, at , mM tTX X where M X is the value of () m X tT at m tT or equiva- lently at 1n. The corresponding solution holds only for m tT and is given by 2 () exp m mM Tt Xt TXCf (23) M X can be determined from (18) by using m tT . /2NC Then, by using (20) the above expression takes the form of Equation (24). It would be reasonable to express 0 X as a fraction of max X for any learner. Taking into account the expres- sion of max X we may have 12 0max 12 1 f f XX f f , with 01 (25) Now using (24) and (25) we obtain 1 max max 2 (1 ) () 11expexp 22 m Nf N n Xt TXXf (26) The behavior of X, as a function of n, is obtained from (22) and (26) for the ranges 01n and 1n resp- ectively (see Figures 5-7). 5. Applications Let us now consider the learning behaviour for a group of students, preparing for a certain examination proc- ess.The time allotted for preparation before the examina- tion is 1 T. Let h X be the information gathered by the best learner. Hence using 12 1ff, 1 tT and max (/2C ) again. 1 0max 11 exp 22 h T XX (27) A student may make some delay while starting the process of learning. Let 1 T be the time utilized by any arbitrary learner where 01 . The delay in starting the learning process is1 (1 )T . Let us define as the utilization index. For the most sincere student = 1. Let a X be the amount of knowledge acquired by any arbitrary learner before the commencement of examina- tion. Thus fora X X at 1 tT with 2 12 1 Cf ff we have 12 121 0 12 12 exp 11 a ff ffT XX ff ff (28) The performance of any arbitrary student in an exami- nation, relative to the best learner, can be defined as 12 121 0 12 12 1 0max exp 11 11 exp 22 a r h ff ffT X ff ff X PXT X (29) Let us call r P the relative performance index. We can always express 1 T as a multiple of max as 1max 2 C T , with 0 (30) Assuming 00X and substituting for 1 T and we get see (Figures 8-13) . 2 )1( exp 2 )1( exp 11 )( 22 21 0 21 21 21 21 f nN f ffN X ff ff ff ff TtXm (24)  A Mathematical Study of the Dynamics of Conscious Acquiring of Knowledge Through Reading and Cramming and the Process of Losing Information from the Brain by Natural Forgetting of Facts Copyright © 2010 SciRes. PSYCH 257 12 1212 12 122 22 (1) exp 11 2 1exp( ) a r h f fff ff ff fff X PX (31) Defining 12 12 2 1 f f K f f we obtain 1 1exp 1-exp(- ) r f KK P (32) When the time available for study is sufficiently long, for a sincere learner (with 1 ), the exponential terms in the last equation become negligible and it will reduce to 12 12 2 1 r f f PK f f (33) Using experimental results one can determine C and 2 f . Let us suppose somebody performs two tests of Figure 5. Graphical representation of (22), (23) and (24) with parametric variations. Figure 6. Graphical representation of (22), (23) and (24) with parametric variations. Figure 7. Graphical representation of (22), (23) and (24) with parametric variations. Figure 8. r P -1 f variation for three different2 f , drawn on the basis of (31) Figure 9. r P -2 f variation for three different 1 f , drawn on the basis of (31). Figure 10. r P –1 f variation for three different , drawn on the basis of (31). 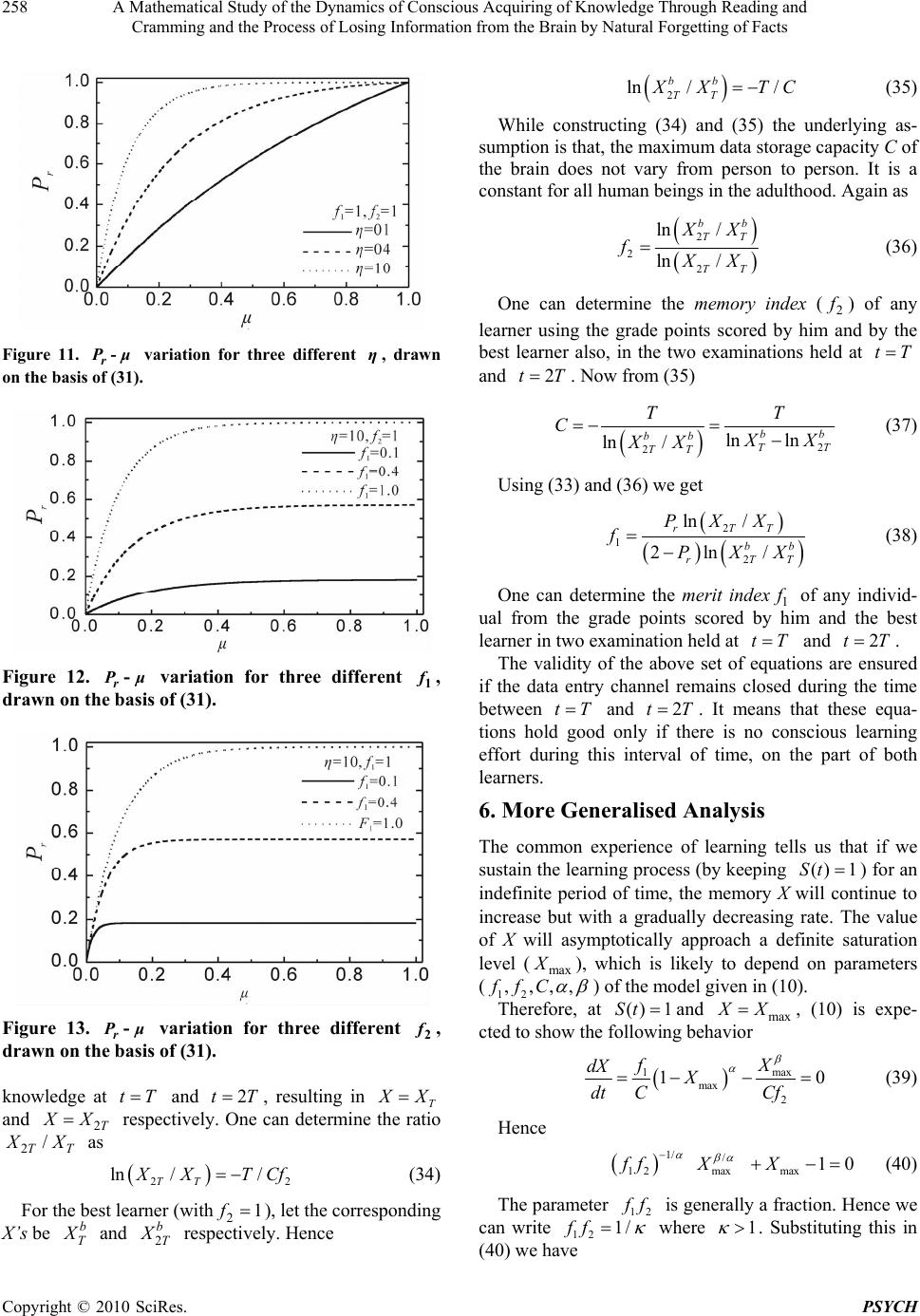 A Mathematical Study of the Dynamics of Conscious Acquiring of Knowledge Through Reading and Cramming and the Process of Losing Information from the Brain by Natural Forgetting of Facts Copyright © 2010 SciRes. PSYCH 258 Figure 11. r P - μ variation for three different η, drawn on the basis of (31). Figure 12. r P - μ variation for three different 1 f , drawn on the basis of (3 1). Figure 13. r P - μ variation for three different 2 f , drawn on the basis of (3 1). knowledge at tT and 2tT, resulting in T X X and 2T X X respectively. One can determine the ratio 2/ TT X X as 22 ln // TT X XTCf (34) For the best learner (with21f ), let the corresponding X’s be b T X and 2 b T X respectively. Hence 2 ln // bb TT X XTC (35) While constructing (34) and (35) the underlying as- sumption is that, the maximum data storage capacity C of the brain does not vary from person to person. It is a constant for all human beings in the adulthood. Again as 2 22 ln / ln / bb TT TT X X f X X (36) One can determine the memory index (2 f ) of any learner using the grade points scored by him and by the best learner also, in the two examinations held at tT and 2tT . Now from (35) 2 2ln ln ln /bb bb TT TT TT C X X XX (37) Using (33) and (36) we get 2 1 2 ln / 2ln/ rTT bb rTT PXX fPXX (38) One can determine the merit index1 f of any individ- ual from the grade points scored by him and the best learner in two examination held at tT and 2tT . The validity of the above set of equations are ensured if the data entry channel remains closed during the time between tT and 2tT . It means that these equa- tions hold good only if there is no conscious learning effort during this interval of time, on the part of both learners. 6. More Generalised Analysis The common experience of learning tells us that if we sustain the learning process (by keeping () 1St ) for an indefinite period of time, the memory X will continue to increase but with a gradually decreasing rate. The value of X will asymptotically approach a definite saturation level (max X), which is likely to depend on parameters (12 ,,,,ffC ) of the model given in (10). Therefore, at () 1St and max XX, (10) is expe- cted to show the following behavior max 1max 2 10 X f dX X dt CCf (39) Hence 1/ / 12max max 10ff XX (40) The parameter 12 f f is generally a fraction. Hence we can write 12 1/ff where 1 . Substituting this in (40) we have  A Mathematical Study of the Dynamics of Conscious Acquiring of Knowledge Through Reading and Cramming and the Process of Losing Information from the Brain by Natural Forgetting of Facts Copyright © 2010 SciRes. PSYCH 259 1/ / max max 10XX (41) The real solutions of this polynomial are the intersec- tions of the curve 1/ max yX with straight line max 1yX . For max 1X, the curve will never have 0y as obtained for the straight line. Thus, we always have max 1X which means that a learner will always have x C. Theoretically, the highest possible value of (/) X xC is 1. Here we have to consider the particular real and positivemax X (we definitely have some positive roots as all the parameters are positive) which is less than 1. For an individual learner, it is always desirable to have a saturation value (max X) that is as close to 1 as possible. To ensure it, the curve 1/ max yX must be very flat. Since max 01X, for a sufficiently large value of we must have max 1X . Hence, for this large value of , one can increase the flatness of the curve by re- ducing the value of . From the definitions of and it is clear that, persons with larger values of the ratio / must make better learning performances. Here we see that larger values of this ratio increase the flatness of the curve 1/ max yX , making max X closer to 1. In Figure 14, we have a plot of max X as a function of / for three different values of . Any of these curves shows that as the ratio / increases, max X increases. At any fixed value of / , the value of max X increases as increases. It is important to calculate the time required for reach- ing the saturation level. We know that, as t, we have max XX, where max X is the saturation value. One can calculate the time required to reach a certain fraction of max X. Let us define optimum time (opt T) as the time required to reach 99% of the saturation value. Putting () 1St in (10) we find an analytical expres- sion for opt T as 0.99 2 12 max (1 ) X opt Xin dX TCf f fXX (42) Here, in X indicates the initial amount of memory at t = 0. (42) shows that the in tegrand diminishes for smaller values of and larger values of since01X . Therefore, the ratio / may be expected to play a significant role here. This integrand also decreases for any increase in the value of the quantity 12 f f. For a definite set of numerical values of the model-parameters we can estimate opt T numerically from (42) and can compare it with m T For any learner it is desirable to maximize max X and minimize opt T. Let us consider a situation that allows one to continue the conscious learning process up to the time of m tT . Figure 14. Variation of max X as a function of β/α for different values of β for C = 10, f1 = 0.6, f2 = 0.6, ε= 1000000, T = 200, X0 = 0, S(t) = 1. Thus, fromm tT onwards we have ()0St . Here, m T may be the time given for preparation before any test of learning. Comparing m T with opt T, let us dis- cuss different possible cases below. a) mopt TT: In this case the learner gets the percep- tion of reaching the saturation level before having to stop the learning process. b) m opt TT : Here, the learner just reaches the satura- tion level at the end of the time interval given for learn- ing. It is worse compared to the last case. c) m opt TT : This situation is the most undesirable one. Here the learner has to stop the process before at- taining the saturation level of learning. To explor e the role played by the ratio / , we may define average learning speed (av S) as follows max 0.99 av opt X ST (43) In Figure 15, we have a plot of av S as a function of the ratio / for three different values of . Each curve has an increasing trend with a gradually decreasing slope. Although these curves have intersections with each other at lower values of / , at higher values of this ratio, av S becomes larger for greater values of . Let us now analyze the situation after one stop the learn- ing process at m tT . The system now follows the (11). Since we have already discussed cases with 1 earlier, we should now consider the cases with 1 . Consid- ering the boundary condition that k X X at m tT , we may write 1 1 2 (1 )1 mk TtX XCf (44) 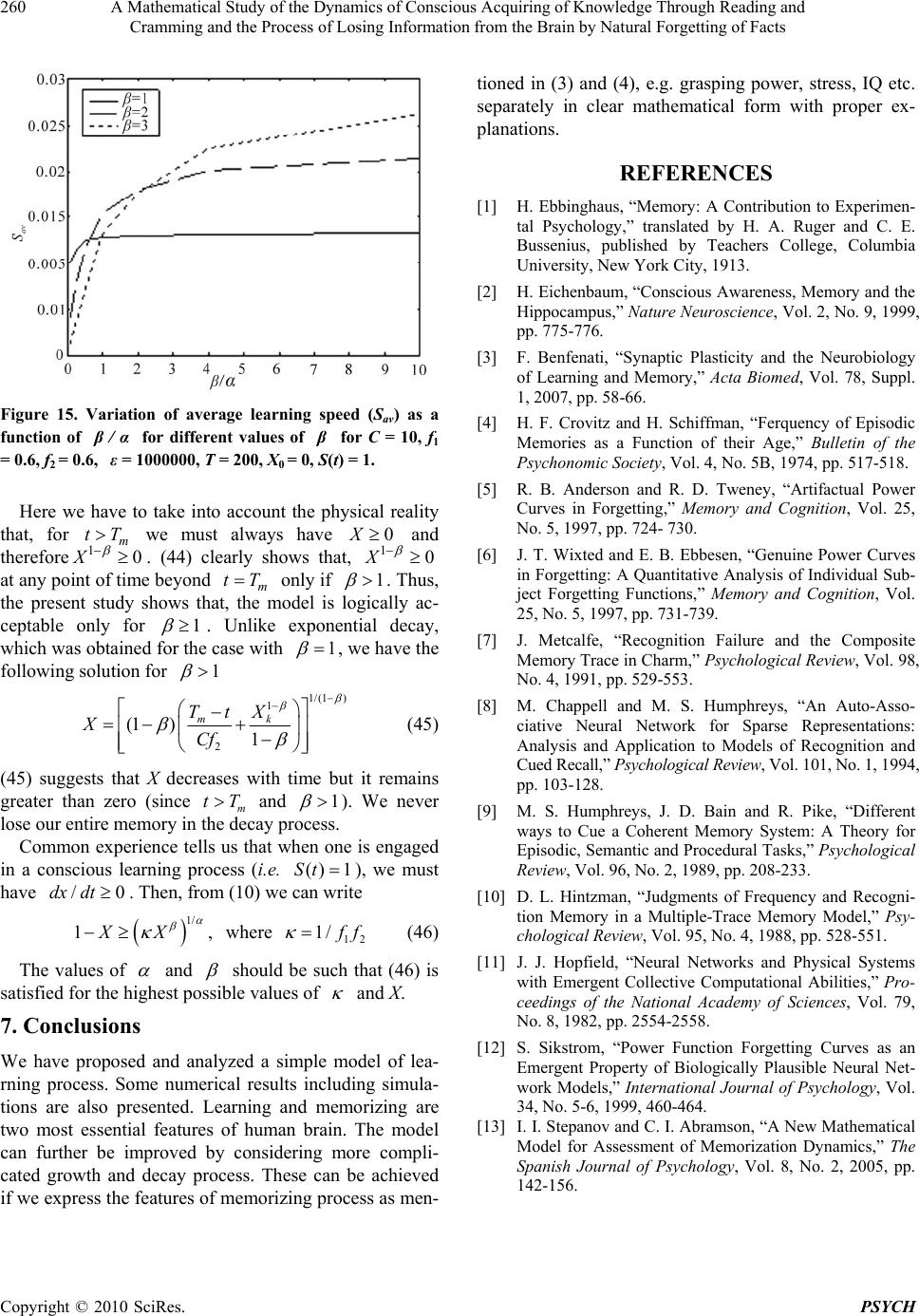 A Mathematical Study of the Dynamics of Conscious Acquiring of Knowledge Through Reading and Cramming and the Process of Losing Information from the Brain by Natural Forgetting of Facts Copyright © 2010 SciRes. PSYCH 260 Figure 15. Variation of average learning speed (Sav) as a function of β/α for different values of β for C = 10, f1 = 0.6, f2 = 0.6, ε= 1000000, T = 200, X0 = 0, S(t) = 1. Here we have to take into account the physical reality that, for m tT we must always have 0X and therefore 10X . (44) clearly shows that, 10X at any point of time beyond m tT only if 1 . Thus, the present study shows that, the model is logically ac- ceptable only for 1 . Unlike exponential decay, which was obtained for the case with 1 , we have the following solution for 1 1/(1 ) 1 2 (1 )1 mk TtX XCf (45) (45) suggests that X decreases with time but it remains greater than zero (since m tT and 1 ). We never lose our entire memory in the decay process. Common experience tells us that when one is engaged in a conscious learning process (i.e. () 1St ), we must have /0dxdt . Then, from (10) we can write 1/ 1,XX where 12 1/ f f (46) The values of and should be such that (46) is satisfied for the highest possible values of and X. 7. Conclusions We have proposed and analyzed a simple model of lea- rning process. Some numerical results including simula- tions are also presented. Learning and memorizing are two most essential features of human brain. The model can further be improved by considering more compli- cated growth and decay process. These can be achieved if we express the features of memorizing process as men- tioned in (3) and (4), e.g. grasping power, stress, IQ etc. separately in clear mathematical form with proper ex- planations. REFERENCES [1] H. Ebbinghaus, “Memory: A Contribution to Experimen- tal Psychology,” translated by H. A. Ruger and C. E. Bussenius, published by Teachers College, Columbia University, New York City, 1913. [2] H. Eichenbaum, “Conscious Awareness, Memory and the Hippocampus,” Nature Neuroscience, Vol. 2, No. 9, 1999, pp. 775-776. [3] F. Benfenati, “Synaptic Plasticity and the Neurobiology of Learning and Memory,” Acta Biomed, Vol. 78, Suppl. 1, 2007, pp. 58-66. [4] H. F. Crovitz and H. Schiffman, “Ferquency of Episodic Memories as a Function of their Age,” Bulletin of the Psychonomic Society, Vol. 4, No. 5B, 1974, pp. 517-518. [5] R. B. Anderson and R. D. Tweney, “Artifactual Power Curves in Forgetting,” Memory and Cognition, Vol. 25, No. 5, 1997, pp. 724- 730. [6] J. T. Wixted and E. B. Ebbesen, “Genuine Power Curves in Forgetting: A Quantitative Analysis of Individual Sub- ject Forgetting Functions,” Memory and Cognition, Vol. 25, No. 5, 1997, pp. 731-739. [7] J. Metcalfe, “Recognition Failure and the Composite Memory Trace in Charm,” Psychological Review, Vol. 98, No. 4, 1991, pp. 529-553. [8] M. Chappell and M. S. Humphreys, “An Auto-Asso- ciative Neural Network for Sparse Representations: Analysis and Application to Models of Recognition and Cued Recall,” Psychological Review, Vol. 101, No. 1, 1994, pp. 103-128. [9] M. S. Humphreys, J. D. Bain and R. Pike, “Different ways to Cue a Coherent Memory System: A Theory for Episodic, Semantic and Procedural Tasks,” Psychological Review, Vol. 96, No. 2, 1989, pp. 208-233. [10] D. L. Hintzman, “Judgments of Frequency and Recogni- tion Memory in a Multiple-Trace Memory Model,” Psy- chological Review, Vol. 95, No. 4, 1988, pp. 528-551. [11] J. J. Hopfield, “Neural Networks and Physical Systems with Emergent Collective Computational Abilities,” Pro- ceedings of the National Academy of Sciences, Vol. 79, No. 8, 1982, pp. 2554-2558. [12] S. Sikstrom, “Power Function Forgetting Curves as an Emergent Property of Biologically Plausible Neural Net- work Models,” International Journal of Psychology, Vol. 34, No. 5-6, 1999, 460-464. [13] I. I. Stepanov and C. I. Abramson, “A New Mathematical Model for Assessment of Memorization Dynamics,” The Spanish Journal of Psychology, Vol. 8, No. 2, 2005, pp. 142-156. |

