Pharmacology & Pharmacy, 2010, 1, 60-68
doi:10.4236/pp.2010.12009 Published Online October 2010 (http://www.SciRP.org/journal/pp)
Structure Analysis for Hydrate Models of
Ethyleneimine Oligomer by Quantum
Chemical Calculation
Minoru Kobayashi1, Hisaya Sato2
1Graduate School of Bio-Applications and Systems Engineering, Tokyo University of Agriculture and Technology, Tokyo, Japan;
2Graduate School of Technical Management, Tokyo University of Agriculture and Technology, Tokyo, Japan.
Received June 14th, 2010; revised July 14th, 2010; accepted August 10th, 2010.
ABSTRACT
Structure analyses for hydrate models of ethyleneimine oligomer (5-mer as model of PEI) were investigated by quantum
chemical calculations. Conformation energies and structures optimized for hydrate models of (ttt)5 and (tgt)5 conform-
ers were examined. Hydrate ratio, h [h = H2O/N (mol)], was set from 0.5 to 2. In anhydrates, (tg+t)5 conformer was
more stable (−1.8 kcal/m.u.) than (ttt)5. In hydrates, (ttt)5 conformers were more stable (−0.7 - −4.3) than (tg+t)5. These
results corresponded to experimental results that anhydrous linear PEI crystal changes from double helical to single
planar chain in hydration process. Structures calculated for (ttt)5 agreed in those observed for hydrates of PEI. In all
(tg+t)5 conformers, O···H bonds between waters were found with the decreases of N···H bonds between imino group and
water. The O···H bonds in (tg+t)5 conformer resulted in its high chain torsion, and strongly related with instability and
structure change (large swelling).
Keywords: Structure Analysis, Conformation, Hydrate, Poly(Ethyleneimine), Oligomer, Quantum Chemical Calculation
1. Introduction
Linear poly(ethyleneimine) (PEI, (-CH2CH2NH-)n) ex-
hibits various kinds of crystalline phases. X-Ray diffrac-
tion (XRD) [1-3] and time-resolved infrared spectral
measurement [4] have confirmed that the structure of
anhydrate is a 5/1 double stranded helix with a repeating
tgt (t: trans, g: gauche) conformation for N-C, C-C, and
C-N bonds, and in the hydrate, the structure transforms to
the planar zigzag with ttt conformation. In hydration
process, the anhydrate changes to the hemi-hydrate
(H2O/EI = 0.5/1 mol), subsequently the sesqui-hydrate
(H2O/EI = 1.5/1), and finally the di-hydrate (H2O/EI =
2/1) with increasing water contents. The mechanism of
such characteristic transitions, however, is not yet clear.
The understanding of the mechanism is important also in
relation with the biological problem of double stranded
DNA chains.
To complement the experimental observations in the
conformations of PEI, computational chemistry has been
employed. Analyses for anhydrate models using molecu-
lar mechanics (MM) and molecular dynamics (MD) have
been reported [5,6]. Furthermore, recent studies involve
quantum chemical calculations method (QCC) [7-9]. The
reports concerning an analysis using hydrate model of
PEI, however, seem to be little [10]. We have investi-
gated the conformation analyses for EI oligomer models
by QCC [11-12]. Most recently, for the hydrate models
with various conformations ((ttt)x, (ttg+)x, (tg+t)x, (tg+g+)x,
(tg+g-)x, and (g+g+g+)x, x: monomer units number; x = 1 –
8) of EI oligomers, we reported [13] that the (tg+t)x and
(ttt)x conformers are the most stable in anhydrate and
hydrate (hydrate ratio: h (H2O/N (mol) = 1), respectively,
and the stabilities of conformers seemed to be related
with hydrogen bonding between water molecules. How-
ever, the details of mechanism in such transfer from
(tg+t)x to (ttt)x were not yet clear.
In this study, in order to deepen an understanding to
the mechanism of such transfer of PEI in hydration proc-
ess, the structure analyses for hydrate models of EI oli-
gomer were investigated by QCC in more detail. The
5-mer model (single chain) as PEI model was used. The
conformation energies and structures of only the (ttt)5 or
(tgt)5 conformer with various hydrate ratios were esti-

Structure Analysis for Hydrate Models of Ethyleneimine Oligomer by Quantum Chemical Calculation 61
mated from the optimized structures. The conformational
characteristics of hydrates were discussed, and were
compared with the experimental results observed for
PEI’s crystals in hydration process.
2. Calculation
2.1. Designations of Anhydrate Models
For anhydrate model, EI 5-mer capped with N-methylimino
and methyl group (single chain: CH3NH-(CH2CH2NH)5-
CH3) was used. For its conformation, the (ttt)5 and (tgt)5
conformers were prepared. The conformations: (τnτn+1
τn+2)x = 5 (τ: dihedral angles, n: sequential number of at-
oms along a skeletal chain, x: monomer units number)
were designated for the combination of τ that are re-
peated for the units of N-C, C-C, and C-N bonds. Every
dihedral angle was independently assigned along the
skeletal chains. The descriptive example designated for
the model (EI 1-mer) as ethyleneimine monomer is given
in Figure 1. As reported in our previous paper [11], the
conformation energies optimized for anhydrate models of
EI oligomers (1 - 11-mer) using QCC (by RHF/6-31 +
G(d,p) basis set) affected by the designation values for
the trans conformation. All the most stable conformers
were obtained by using the designation values for trans
as follow: (τn/τn+1/τn+2)x was (−175°/−175°/180°(π))x,
whose pseudo-asymmetries based on a nitrogen inversion
were racemo. This designation system is partially re-
stricted system, which was defined as that restricted from
π to a unidirectional angle as trans helical condition. In
this study, therefore, this system was used for the design-
nations of trans values of dihedral angle. For the (tg+t)5
conformer, (−170°/ + 60°/180°(π))x = 5 was used as (τn/τn+1/
τn+2) x = 5 value.
2.2. Designations of Hydrate Models
Hydrate models were prepared by locating water mole-
cule near the nitrogen atom in the optimized structures
for anhydrate. The optimization for anhydrate was car-
ried out firstly using RHF/STO-3G and then RHF/6-31G
basis sets. The specified models are given in Table 1.
Hydrate ratio (h) was defined by H2Omol/Nmol in oligomer,
and the values of 0.5-2 were set. Two types of models
were used: in one model water molecules are attached to
discontinuous monomer units (α type) and in the other to
continuous monomer units (β type) as shown in Table 1.
The structure designated for EI 1-mer as a descriptive
example is given in Figure 1. Hydrate distance (dN-H, (Å))
was defined by the unbonded distance between the near-
est nitrogen atom (N) and hydrogen atom (H) of HOH’ in
which H atom is closer to the nitrogen atom than H’ atom
as shown in Figure 1. For all conformers except for the
(tg+t)5 conformers with h = 1.5 and 2, the value of 1.7 Å
was used as dN-H, according to the results in our previous
report [13] in which the effects of designations of dN-H on
the optimized structures were examined to the experi-
mental results. In the (tg+t)5 conformers with h = 1.5 and
2, the dN-H values of 1.7 and 5.2 Å for a di-hydrate NH
unit were used in order to avoid a crowding of water
molecules in designation structure. The direction effects
in location of water molecule (to N or H in NH group) on
the optimized structures and energies were not found.
Figure 1. Descriptive examples of designated and optimized structures for hydrate model of ethylenimine monomer (EI 1-mer,
conformation: (ttt)1, h = 0.5, α type, (- - -: hydrogen bond). Conformation was defined by (τnτn+1τn+2)x=1, where τn, τn+1, and
τn+2 are the dihedral angles (°) for N-C, C-C, and C-N bonds, respectively, and x is monomer unit number. In “Dseignated” of
the figure, −175°, −175°, and π as the dihedral angles (τn, τn+1, and τn+2: partially restricted system) were used for N2-C3,
C3-C5, and C5-N7 bonds, respectively. Hydrate distance (dN-H, (Å)) was defined in hydrogen bonded NH group and water
(N···H, N2-H6) as shown in “Optimized” in the figure. Conformer length was defined by L (Å), where L is unbonded distance
between the terminal nitrogen atoms: N2-N7 in the figure.

Structure Analysis for Hydrate Models of Ethyleneimine Oligomer by Quantum Chemical Calculation 62
Table 1. Hydrate models for ethyleneimine oligomer (EI 5-
mer).
Hydrate models1
No. Models
Hydrate
type
Number of
H2O: Nw
Hydrate ratio:
h (H2O/N, mol)
1 N-N-N-N-N-N - 0 0.000
2 N-N-N-N-N-N α 3 0.500
3 N-N-N-N-N-N β 3 0.500
4 N-N-N-N-N-N β 4 0.667
5 N-N-N-N-N-N β 5 0.833
6 N-N-N-N-N-N β 6 1.000
7 Ň-N-Ň-N-Ň-N β 9 1.500
8 Ň-Ň-Ň-Ň-Ň-Ň β 12 2.000
1N and Ň show the mono- and di-hydrated nitrogen units, respectively, (N =
RNHR’, R or R’ = CH3 or CH2CH2). The α and β show discontinuous and
continuous hydrate units, respectively.
2.3. Structure Optimizations
Structure optimizations were carried out for each model
using QCC via the Gaussian 03W (Gaussian Inc.) pro-
gram [14], according to the methods in our previous re-
port [13]. RHF/6-31G basis set was used. Gross energy
of hydrated conformer with waters, Eh (Hartree, 1 Har-
tree = 627.51 kcal/mol), was calculated. Conformation
energy of conformer, Ec (Hartree) was calculated via
Equations (1) and (2),
ch w
EE E
 (1)
() ()wwn wh
EE E
 (2)
where ∑Ew is the total energy of water molecules. Ew(n)
and Ew(h) are the energies of non-hydrogen and hydrogen
bonded water molecules, respectively.
The Ew(n) was calculated for the model of non-hydrogen
bonded water molecules which are consisted of n units of
single water molecule by RHF/6-31G basis set (refer
Table 2). As the unit number (n) in the calculation of
Ew(n), the number of water molecules (Nw(n)) with
non-hydrogen bonded water molecules, which was esti-
mated in the structures optimized for the hydrate models,
was used (refer Table 4, Figure 2 and Figure 3). In the
same way, the Ew(h) was calculated for the model of line-
arly hydrogen bonded water molecules which are con-
sisted of n units of sequential water molecules. As n in
the calculation of Ew(h), the number of water molecules
(Nw(h)) with hydrogen bonded water molecules was used.
Hydrogen bond (O···H bond) between water molecules
was confirmed by the unbonded O···O distance (dO-O)
between water molecules. The dO-O values in non-hydro-
Table 2. Energies (Ew, HF) calculated for water molecules
by RHF/6-31G.
n1 Ew(n)2 Ew(h)3 n1 Ew(n)2 Ew(h)3
1 −75.9854- 5 −379.9274 −379.9876
2 −151.9708 −151.9826 6 −455.9128 −455.9907
3 −227.9562 −227.9830 9 −683.8686 −684.0007
4 −303.9416 −303.9850 12 −911.8256 −912.0114
1Units number of water molecules. 2Energies of non-hydrogen bonded water
molecules. 3Energies of linearly hydrogen bonded water molecules which
are consisted of n units of sequential water molecules (dO-O calculated: 2.71
- 2.85 Å).
gen and hydrogen bonded water molecules were defined
as the larger and smaller value than 3 Å, respectively,
according to the results observed for water dimer (dO-O:
2.74 Å in regular ice [15], 2.85 Å in liquid [15], and 2.98
Å in vapor [16,17]). The dO-O values in O···H bonded
water molecules estimated for the models of water mo-
lecules were smaller than 3 Å. The calculated Ew(n) and
Ew(h) values are given in Table 2. The examples for con-
formation energies (Ec) are given in Table 3.
The conformation in optimized structure was specified
based on IUPAC [18] as follow: τn of trans (t±) and
gauche (g±) are from ± 120° to ± 180° and from ± 0° to ±
120°, respectively. Hydrate distance (dN-H, (Å)) was de-
fined as mentioned before, and its example is shown in
Figure 1. Another parameter for hydrate distance was
defined by dN-O (Å), where dN-O is unbonded distance
between nitrogen atom (N) of imino group and oxygen
atom (O) of neighboring water molecule. The dN-O value
in hydrogen bonded (N···H bond) imino group/water
molecule was defined as smaller value than 3 Å (dN-H < 2
Å) according to the results observed for hydrous PEI’s
crystals (dN-O: 2.87 - 3.05 [2,3], see Table 5). Conformer
length was defined by L (Å), where L is unbonded dis-
tance between terminal nitrogen atoms as shown in foot-
note of Figure 1. Diameter of (tgt)5 conformer was de-
fined by D (Å), where D is relative diameter which was
measured as the largest value in chain axis projection for
optimized structure based on D value of anhydrate.
3. Results and Discussion
3.1. Conformation Energies (Ec) Calculated for
Hydrate Models of (ttt)5 and (tg+t)5
Conformers
The structures optimized for the hydrate models of (ttt)5
and (tg+t)5 conformers of EI 5-mer as model of PEI were
examined. In Figures 2 and 3, the examples of structures
optimized for (ttt)5 and (tg+t)5 conformers are shown,
respectively. In both figures, the hydrogen bonds with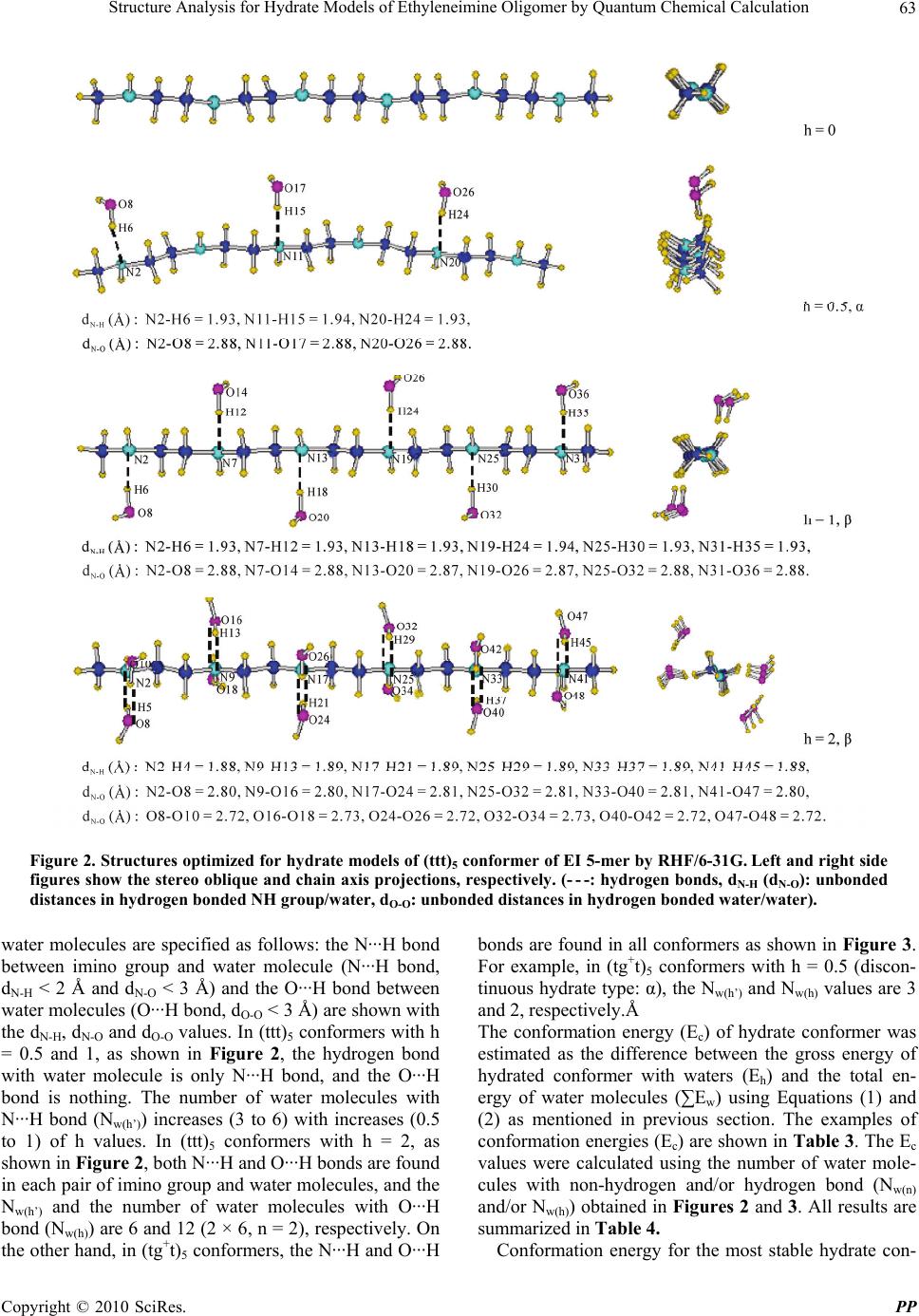

Structure Analysis for Hydrate Models of Ethyleneimine Oligomer by Quantum Chemical Calculation 63
Figure 2. Structures optimized for hydrate models of (ttt)5 conformer of EI 5-mer by RHF/6-31G. Left and right side
figures show the stereo oblique and chain axis projections, respectively. (- - -: hydrogen bonds, dN-H (dN-O): unbonded
distances in hydrogen bonded NH group/water, dO-O: unbonded distances in hydrogen bonded water/water).
water molecules are specified as follows: the N···H bond
between imino group and water molecule (N···H bond,
dN-H < 2 Å and dN-O < 3 Å) and the O···H bond between
water molecules (O···H bond, dO-O < 3 Å) are shown with
the dN-H, dN-O and dO-O values. In (ttt)5 conformers with h
= 0.5 and 1, as shown in Figure 2, the hydrogen bond
with water molecule is only N···H bond, and the O···H
bond is nothing. The number of water molecules with
N···H bond (Nw(h’)) increases (3 to 6) with increases (0.5
to 1) of h values. In (ttt)5 conformers with h = 2, as
shown in Figure 2, both N···H and O···H bonds are found
in each pair of imino group and water molecules, and the
Nw(h’) and the number of water molecules with O···H
bond (Nw(h)) are 6 and 12 (2 × 6, n = 2), respectively. On
the other hand, in (tg+t)5 conformers, the N···H and O···H
bonds are found in all conformers as shown in Figure 3.
For example, in (tg+t)5 conformers with h = 0.5 (discon-
tinuous hydrate type: α), the Nw(h’) and Nw(h) values are 3
and 2, respectively.Å
The conformation energy (Ec) of hydrate conformer was
estimated as the difference between the gross energy of
hydrated conformer with waters (Eh) and the total en-
ergy of water molecules (∑Ew) using Equations (1) and
(2) as mentioned in previous section. The examples of
conformation energies (Ec) are shown in Table 3. The Ec
values were calculated using the number of water mole-
cules with non-hydrogen and/or hydrogen bond (Nw(n)
and/or Nw(h)) obtained in Figures 2 and 3. All results are
summarized in Table 4.
Conformation energy for the most stable hydrate con-

Structure Analysis for Hydrate Models of Ethyleneimine Oligomer by Quantum Chemical Calculation 64
Figure 3. Structures optimized for hydrate models of (tg+t)5 conformer of EI 5-mer by RHF/6-31G. Left and right side
figures show the stereo oblique and chain axis projections, respectively. (- - -: hydrogen bond, dN-H (dN-O): unbonded
distance in hydrogen bonded NH group/water, dO-O: unbonded distance in hydrogen bonded water/water).

Structure Analysis for Hydrate Models of Ethyleneimine Oligomer by Quantum Chemical Calculation 65
Table 3. Examples of conformation energies (Ec) (Model: No. 2 (h = 0.5, hydrtate type: α), by RHF/6-31G).
Water molecules
Non-hydrogen bonds Hydrogen bonds
Conformations Eh (HF) Number of
water (Nw)1 Nw(n)2 E
w(n) (HF) Nw(h)4 E w(h) (HF)3
∑Ew (HF)
Ec (HF)
(ttt)5 −1027.2999 3 3 −227.9562 0 0 −227.9562 −799.3437
(tg+t)5 −1027.3266 3 1 −75.9854 2 −151.9826 −227.9680 −799.3586
1Nw = Nw(n) + Nw(h). 2Number of water molecules with non-hydrogen bond (dO-O ≥ 3 Å), obtained in Figure 2 or 3. 3From Table 2. 4Number of water molecules
with hydrogen bond (O···H, dO-O < 3 Å), obtained in Figure 2 or 3.
Table 4. Structure analyses for hydrate models of ethyleneimine oligomer (EI 5-mer) by RHF/6-31G.
Models No.1 No.2 No.3 No.4 No.5 No.6 No. 7 No.8
Number of
water: Nw 0 3 3 4 5 6 9 12
Hydrate
ratios: h 0 0.5 (α) 0.5 (β) 0.67 (β) 0.83 (β) 1 (β) 1.5 (β) 2 (β)
Eh (HF) −799.3040 −1027.2999 −1027.2990 −1103.2996 −1179.2976 −1255.2968 −1483.3103 −1711.3289
Nw(n) / Nw(h) - 3/0 3/0 4/0 5/0 6/0 3/(2 × 3) 0/(2 × 6)
Nw(h’) 1 - 3 3 4 5 6 6 6
∑Ew (HF) - −227.9562 −227.9562 −303.9416 −379.9274 −455.9128 −683.9040 −911.8956
Ec (HF) −799.3040 −799.3437 −799.3428 −799.3580 −799.3702 −799.3840 −799.4063 −799.4333
∆Ec
(kcal/m.u.)2 0.00 −4.98 −4.87 −6.78 -8.31 -10.1 12.8 -16.2
τn (°)3 −180.0 −179.6 179.1 −178.7 178.4 179.0 177.9 179.3
N-H’N’ /
N’-HN (Å)4 4.01/4.01 4.01/4.02 4.01/4.01 4.02/4.02 4.01/4.01 4.02/4.02 4.01/4.00 4.00/4.00
2 mol length
(Å)5 7.35 7.35 7.37 7.38 7.38 7.37 7.37 7.37
(ttt)5
L (Å) 18.38 18.31 18.41 18.42 18.43 18.44 18.42 18.44
Eh (HF) −799.3183 −1027.3266 −1027.3299 −1103.3372 −1179.3459 −1255.3603 −1483.3851 −1711.4103
Nw(n) / Nw(h) - 1/2 0/3 0/4 0/5 0/6 0/9 0/12
Nw(h’) 1 - 3 2 3 4 4 5 5
∑Ew (HF) - −227.9680 −227.9830 −303.9850 −379.9876 −455.9907 −684.0007 −912.0114
Ec (HF) −799.3183 −799.3586 −799.3467 −799.3522 −799.3583 −799.3696 −799.3844 −799.3989
∆Ec
(kcal/m.u.)2 −1.79 −6.85 −5.36 −6.05 −6.81 −8.23 −10.1 −11.9
τn (°)3 62.7 66.5 61.5 59.9 61.6 62.3 56.7 58.7
N-H’N’ /
N’-HN (Å)4 2.48/3.2 2.74/3.18 2.57/3.15 2.58/3.08 3.68/3.12 2.69/3.17 2.61/2.98 2.54/3.02
5 mol length
(Å)5 13.90 7.82 13.44 12.07 12.09 6.91 10.10 11.30
L (Å) 13.57 8.66 12.93 11.84 11.93 6.99 10.81 11.59
(tg+t)5
D (Å) 1.0 1.94 1.23 1.57 1.57 1.91 1.60 1.43
1Number of water molecules with hydrogen bond (N···H, dN-H < 2 Å and dN-O < 3 Å) between imino group and water. 2Based on Ec of (ttt)5 conformer with h =
0. 3Average of dihedral angles for C-C bonds. 4N-H’N’ (or N’-HN) is average of unbonded distance between N of NH group and H’ of neighboring N’H’ group
(or between N’ and H). 5Average value.
former will be defined as the smallest value of the sum-
mation of anhydrate energy and hydration stability en-
ergy [19]. The hydration stability energy (∆Ec, kcal/m.u.,
m.u.: monomer unit) is given as the difference between

Structure Analysis for Hydrate Models of Ethyleneimine Oligomer by Quantum Chemical Calculation 66
Table 5. Comparison between the calculated and observed structures.
Observed for hydrous linear PEI crystals (by XRD [2,3])
Calculated for hydrate models of (ttt)5 conformer
Hemi-hydrate [2] Sesqui-hydrate [3] Di-hydrate [3]
h = 0.5 (α) h = 1.5 (β) h = 2 (β) h’ = 0.51 h’ = 1.51 h’ = 21
Conformation all trans all trans all trans all trans all trans all trans
2 mol length (Å) 7.35 7.37 7.37 7.312 7.362 7.362
2.88 2.87 2.81 3.05(Na···O1) 2.96(Na···O1) 2.93(Na···O1)
dN-O (Å)
2.87(Na’···O1) 2.93(N···O3)
-3 2.72 2.81 -3 2.87(O1···O2 ) 2.66(O1···O2 )
-
3 2.80 (O1···O3) dO-O (Å)
-
3 2.79(O1···O4 ) 2.75(O1···O4)
1h’: H2O/EI (mol) 2Fiber period, corresponding to 2 mol length. 3Hydrogen bondings between water molecules were not estimated or observed.
the Ec values of anhydrate and hydrate. The results are
shown in Table 4. In Figure 4, the relations between ∆Ec
and h values are shown. The ∆Ec values decreased line-
arly with increases of water contents. In Figure 5, the
Nw(h’) values (with N···H bond) are plotted against hy-
drate ratios (h). The Nw(h’) values increase with increases
of h values until h = 1 ((ttt)5) or 1.5 ((tg+t)5). These re-
sults indicate that the conformers are stabilized by an
electrostatic effect of N···H bond.
In (ttt)5 conformers, as shown in Figure 4, the ∆Ec val-
ues of two conformers with h = 0.5 of α and β (continu-
ous) hydrate type, which have the same value (3) of Nw(h’)
(Figure 5), are almost the same. This result indicates that
the chain torsion effects on ∆Ec in (ttt)5 conformers seem
to be little because of the long distance between
neighboring NH groups in stretched trans structure
(N-H’N’ or N’-HN: 4.01 Å, see Table 4). Although the
Nw(h’) values of (ttt)5 conformers with h = 1.5 and 2 are
the same (6) as that with h = 1 (Figure 5), the ∆Ec values
of the formers are smaller than that of the latter(Figure
4). It seems to be related with the results that the pairs of
water molecules at h = 1.5 or 2 are located in series to
each NH group with O···H bonds as shown in Figure 2.
In (tg+t)5 conformers, as shown in Figure 4, the plots of
∆Ec against h values show linear relation and the con-
formers are stabilized by hydration as same as in (ttt)5
conformers. However, ∆Ec values in h over 0.5 are larger
than those of (ttt)5 conformers. From an energy aspect,
this result corresponds to the experimental results ob-
served for linear PEI’s crystals in hydration process. The
instability of (tg+t)5 conformers seems to be related with
both the increases of O···H bonds and the decreases of
N···H bonds. In (tg+t)5 conformers, the Nw(h) values with
O···H bond increased with increases of h values as shown
in Figure 3 and Table 4. And at the same time, the Nw(h’)
Figure 4. Plots of hydration stability energy (ΔEc, kcal/m.u.)
against hydrate ratios (h). The ● and ○ symbols show (ttt)5
conformers with α and β type, respectively. ▲ and ∆ show
(tg+t)5 conformers with α and β type, respectively.
Figure 5. Plots of Nw(h’) against hydrate ratios (h). The ●
and ○ symbols show (ttt)5 conformers with α and β type,
respectively. The ▲ and ∆ symbols show (tg+t)5 conformers
with α and β type, respectively.

Structure Analysis for Hydrate Models of Ethyleneimine Oligomer by Quantum Chemical Calculation 67
values with N···H bond are smaller than those of (ttt)5
conformers as shown in Figure 5. As shown in Table 4,
the N···H bond distances (N-H’N’ or N’-HN) in neighbor-
ing NH groups of anhydrated (tg+t)5 conformer are
smaller (0.7 - 1.2 Å) than those of (ttt)5 conformer. An-
hydrous PEI’s chain (tgt) is strongly twisted by intra- and
inter-molecular interactions (N···H bonding between
imino groups). Taking into account of these results, the
water molecules coming near to NH groups of (tg+t)5
conformer must strongly prefer to having a pair with
O···H bonds between water molecules compared with
(ttt)5 conformer. For examples in h = 0.5, as shown in
Table 4, the Nw(h) values of (tg+t)5 conformers with α and
β type are larger (2-3) than those of (ttt)5 conformers
with α and β type. Furthermore, the Nw(h) value of (tg+t)5
conformer with β type is larger (1) than that with α type.
3.2. Structures Calculated for Hydrate Models of
(ttt)5 and (tg+t)5 Conformers
In (ttt)5 conformers, as shown in Figure 2 and Table 4,
the structure changes by hydrations are little. It seems to
be related with the results that the effects of O···H bonds
between water molecules on the structures are negligible.
The O···H bonds were not found in conformers with h ≤
1, but were found in the conformers with h = 1.5 and 2.
In h = 1.5 and 2, the O···H bonds are independent in each
hydrate unit (refer Figure 2).
In Table 5, the structures calculated for (ttt)5 con-
formers were compared with those observed for linear
hydrous PEI’s crystals by XRD [2,3]. The 2 mol length
or dN-O value calculated for the conformers with h = 0.5
(α, β type), 1.5 and 2 agreed in that observed for hemi-
(H2O/EI, mol = 0.5) [2], sesqui- (1.5) [3] and di-hydrate
(2) [3], respectively. The results that the O···H bonds
between water molecules were not found in the con-
formers with h = 0.5 (α and β type) corresponded to the
experimental results observed for hemi-hydrate as shown
in Table 5. The dO-O values calculated for the O···H
bonded water molecules in conformers with h = 1.5 and 2
agreed in those observed for sesqui- [3] and di-hydrate
[3]. These agreements in the calculated and observed
results should be noticed. Polymer chains in hydrous
crystal are separated to a single chain (ttt) with hydrogen
bonded water molecule (N···H and/or O···H bond). The
structures calculated for single chain models will be fun-
damentally different from those observed for hydrous
polymer crystals. These agreements seem to be resulted
in “a single chain” in both cases.
As shown in Figure 3, the structure calculated for an-
hydrate model of (tg+t)5 conformer fundamentally corre-
sponded to the structure observed for anhydrous linear
PEI’s crystal (5/1 double stranded helix, tgt [1]). How-
ever, the 5 mol length calculated (13.90 Å, in Table 4)
was different from that observed (9.58 Å [1]). This dif-
ference indicates that the double stranded helical chains
of PEI are largely shrinking and swelling because of their
inter-molecular interactions. The structures calculated for
hydrate models of (tg+t)5 conformer largely changed by
hydrations as shown in Figure 3 and Table 4. The plots
of shrinkage rates (ΔL/L0 (%), L0: conformer length cal-
culated for anhydrate) against h values are shown in
Figure 6. In Figure 7, the swelling rates in (tg+t)5 con-
formers (ΔD/D0 (%), D0: diameter calculated for anhy-
drate) are plotted against h values. As shown in Figures
6 and 7, the (tg+t)5 conformers with h = 0.5 (α type) and 1
(β type) are strongly shrinking and swelling. It seems to
be connected with the results that the water molecules
with O···H bonds are located in the insides of conformers
as shown in Figure 3. Taking into account with the re-
sults of ∆Ec (Figure 4), the strong swelling in (tg+t)5
Figure 6. Plots of chain shrinkage rates (ΔL/L0 (%), ΔL: L -
L0, L0: L of anhydrate) against hydrate ratios (h). The ●
and ○ symbols show (ttt)5 conformers with α and β type,
respectively. The ▲ and ∆ symbols show (tg+t)5 conformers
with α and β type, respectively.
Figure 7. Plots of chain swelling rates (ΔD/D0 (%), ΔD: D -
D0, D0: D of anhydrate) against hydrate ratios (h) in (tg+t)5
conformers. The ▲ and ∆ symbols show α and β type, re-
spectively.

Structure Analysis for Hydrate Models of Ethyleneimine Oligomer by Quantum Chemical Calculation 68
conformers with h values over 0.5 may be one of the
driving forces for dissociation from a double helical
chain to a single planar chain of PEI’s crystal or other
polymer chains as DNA in hydration process.
4. Conclusions
Structure analyses for hydrate models of EI 5-mer as a
PEI’s model were investigated by QCC. In anhydrates,
(tg+t)5 conformer was more stable than (ttt)5 conformer.
In hydrates with hydrate ratios (h) over 0.5, (ttt)5 con-
formers were more stable than (tg+t)5 conformers with
increases of h values. From an aspect of conformation
energy, these results corresponded to the experimental
results that the structure of anhydrous linear PEI’s crystal
changes from helix (tgt) to planar zigzag (ttt) in hydra-
tion process. Structures calculated for hydrates of (ttt)5
conformers agreed in those observed for hydrous PEI
crystals. The instabilities (higher Ec) and structure
changes (swelling) which were estimated for (tg+t)5 con-
formers with hydrate ratios over 0.5 were strongly con-
nected with the formation of O···H bonds between water
molecules affected by the chain torsion, and may be one
of the driving forces for the dissociation of double helical
chains of PEI in hydration process.
REFERENCES
[1] Y. Chatani, T. Kobatake, H. Tadokoro and R. Tanaka,
“Structure Studies of Poly(ethyleneimine). 2. Double-
Stranded Helical Chain in the Anhydrate,” Macromole-
cules, Vol. 15, No. 1, 1982, pp. 170-176.
[2] Y. Chatani, T. Kobatake and H. Tadokoro, “Structure
Studies of Poly(ethyleneimine). 3. Structural Characteri-
zation of Anhydrous and Hydrous States and Crystal
Structure of the Hemihydrate,” Macromolecules, Vol. 16,
No. 2, 1983, pp. 199-204.
[3] Y. Chatani, H. Tadokoro, T. Saegusa and H. Ikeda,
“Structure Studies of Poly(ethyleneimine). 1. Structures
of Two Hydrates of Poly(ethyleneimine): Sesquihydrate
and Dihydrate,” Macromolecules, Vol. 14, No. 2, 1981,
pp. 315-321.
[4] T. Hashida, K. Tashiro, S. Aoshima and Y. Inaki, “Struc-
tural Investigation on Water-Induced Phase Transitions of
Poly(ethyleneimine). 1. Time-Resolved Infrared Spectral
Measurements in the Hydration Process,” Macromole-
cules, Vol. 35, No. 11, 2002, pp. 4330-4336.
[5] H. Dong, J. K. Hyun, C. Durham and R. A. Wheeler,
“Molecular Dynamics Simulations and Poly(ethyleneimine)
Models,” Polymer, Vol. 42, No. 18, 2001, pp. 7809-7817.
[6] S. Wang, L. DeBolt and J. E. Mark, “Configurational
Analysis of Linear Poly(ethyleneimine),” Polymeric Pre-
prints, Vol. 34, No. 2, 1993, pp. 478-479.
[7] S. E. Boesch, S. S. York, R. Frech and R. A. Wheeler,
“An Experimental and Computational Investigation of the
Structure and Vibrations of Dimethylethylenediamine, a
Model for Poly(ethyleneimine),” PhysChemComm, Vol. 4,
2001, pp. 1-10.
[8] Y. Sasanuma, S. Hattori, S. Imazu, S. Ikeda, T. Kaizuka,
T. Iijima, M. Sawanobori, M. A. Azam, R. V. Law and J.
H. G. Steinke, “Conformational Analysis of Poly(ethyl-
eneimine) and its Model Compounds: Rotational and In-
versional Isomerizations and Intramolecular and Intermo-
lecular Hydrogen Bonds,” Macromolecules, Vol. 37, No.
24, 2004, pp. 9169-9183.
[9] H. Kusanagi, “Quantum Chemical Examination on the
Double-Stranded Helix Models of Poly(ethyleneimine),”
Polymer Preprints Japan, Vol. 53, No. 2, 2004, pp.
3610-3611.
[10] D. Diabate, A. Yapo, A. Trokourey, A. Kone and B. Fa-
hys, “Study of Structural and Electronic Properties of
Polyethylenimine Hemihydrate,” Physical and Chemical
News, Vol. 37, 2007, pp. 122-126.
[11] M. Kobayashi and H. Sato, “Conformational Analysis of
Ethylene Oxide and Ethylene Imine Oligomers by Quan-
tum Chemical Calculation,” Polymer Journal, Vol. 40,
No. 4, 2008, pp. 343-349.
[12] M. Kobayashi and H. Sato, “Conformational Analysis of
Ethylene Oxide and Ethylene Imine Oligomers by Quan-
tum Chemical Calculations: Solvent Effects,” Polymer
Bulletin, Vol. 61, No. 4, 2008, pp. 529-540.
[13] M. Kobayashi, M. Takahashi and H. Sato, “Conforma-
tional Analysis for Hydrated Ethylene Imine Oligomer
Models by Quantum Chemical Calculations,” Polymer
Journal, Vol. 41, No. 10, 2009, pp. 880-887.
[14] Gaussian Inc., “Gaussian 03 User’s Reference,” Gaussian
Inc., Pennsylvania, 2003.
[15] R. Ludwig, “Water from Clusters to the Bulk,” Ange-
wandte Chemie International Edition, Vol. 40, No. 10,
2001, pp. 1808-1827.
[16] T. R. Dyke, K. M. Mack and J. S, Muenter, J. Chem.
Phys., Vol. 66, 1977, pp. 498.
[17] J. A. Odutola and T. R. Dyke, “Nitric Acid and Carbox-
ylic Acid Dimers,” Journal of Chemical Physics, Vol. 72,
1980, pp. 50-62.
[18] D. R. Lide, “CRC Handbook of Chemistry and Physics,”
82nd Edition, CRC Press, London, 2001.
[19] M. Kinoshita, Y. Okamoto and F. Hirata, “Solvent Effects
on Formation of Tertiary Structure of Protein,” Biophysi-
cal Society of Japan, Vol. 40, No. 6, 2000, pp. 374-378.